六年级上册数学人教版《数学广角——数与形》(课件)(共35张PPT)
文档属性
| 名称 | 六年级上册数学人教版《数学广角——数与形》(课件)(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 17:41:10 | ||
图片预览











文档简介
(共35张PPT)
数学广角—数与形
人教版小学数学六年级上册
今日数学作业:
1.数学书106页1题、2题;107页1题、2题、3题,做数学书上,并将答案上传到小程序里;
2.一卷通三单元试卷全做,先将应用题和计算题、填空题上传到小程序,再根据答案自行改错,尽量用红笔改了。
网课反思:
1.下次全体成员必须更改备注名,好看到哪些同学进来听课;
2.网课的当天只会上1小时半的课时量,其余时间除了交作业(作业晚上交也可以),尽量让学生远离手机。
3.开学后不会重新再上网课教学内容,最多只是用几天时间复习下上期知识,每学期都有新的学业计划。
1+3=
1+3+5=
1+3+5+7=
1+3+5+7+9+…+15=
看谁算的快。
首尾相加
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
观察这三个算式,你有什么发现?
4
1
9
1
1
2
2
3
3
1×1
=
2×2
3×3
=
=
4
1
9
1
1
2
2
3
3
1×1
=
2×2
3×3
=
=
12
22
32
正方形数
有1个小正方形
每列或每行都有2个小正方形
每列或每行都有3个小正方形
4
1
9
=
=
=
12
22
32
1+3
1+3+5
3
5
1
1、3、5都是 奇数
连续的
1+3+5
32
=
1
=
12
1+3
=
22
从1开始,几个连续的奇数相加,就是几的平方。
1+3+5+……+(2n-1) = n2
n个连续奇数
上面这些图形的问题,需要考虑隐藏着数的规律来解决,这种方法我们称之为数形结合的方法。
数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维。
今天我们就一起来探索数形结合的奥妙!
图形
数与形
华罗庚
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
数字
利用规律直接写一写。
如果遇到困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13 =( )2
1+3+5+7+9+11+13+15+17
4
7
______________________________=( 9 )2
易错点:只有从1开始的连续奇数相加的和才是平方数。
3个奇数
1. 请你根据例1的结论算一算。
1+3+5+7+5+3+1 =( )
25
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
1. 观察图形,填写下表。
43
88
8+5×(n-1)
:按照规律接着画一画,填一填。
3
1
6
10
( )
( )
( )
如果不画,这样排列下去,第10个数是多少?
1+2+3+4+5+6+7+8+9+10=55
这些圆片都可以排成三角形,像这样的数称为三角形数
找规律
如图,摆一个三角形需要3根小棒,摆二个三角形需要5根小棒,摆10个三角形需要 根小棒。
1
三角形个数:
小棒数:
3
2
3+2
3
3+2+2
4
3+2+2+2
1+2×10
3+2×9
规律:
1+2
1+2+2
1+2+2+2
1+2+2+2+2
2×1+1
2×2+1
2×3+1
2×4+1
2×n+1
=2n+1
2. 先数一数,再填一填,用你发现的规律解决问题。
7
9
(1)摆15个三角形,需要多少根小棒?
31根
44个
摆成的三角形个数×2 +1 =所用的小棒根数
(2)有89根小棒,能摆出多少个三角形?
(3)摆成的三角形个数与所用的小棒根数之间有什么关系?
如图,用同样的小棒摆正方形,这样摆20个同样的正方形需要小棒___根
1
正方形个数:
小棒数:
4
2
4+3
3
4+3+3
1+3×20
4+3×19
……
5.下面每个三角形图各是由多少个小三角形组成的
如果小三角形的边长为1,每个三角形图的周长分别是多少
每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系
你还能提出什么数学问题
1
3
4
6
9
9
16
12
请你根据上面图形与数的规律接着画一画,填一填。
如果不画,这样排列下去,第10个数是多少
15
21
28
第10个数是55
1+2+3+4+5
1+2+3+4+5+6
=(1+5)+(2+4)+3
=6+6+3
=3×2+3×2+3
=3×5
=(1+6)+(2+5)+(3+4)
=7+7+7
=7×3
6÷2
(1+6)
5
(1+5)
÷2
首项
末项
+
(
)
项数
×
÷2
等差数列:
相邻两个数之间的差相等
下面算式的和是多少,你能很快地计算出来吗?
1+2+3+4+5+…+10
1+2+2+3+4+5+…+9
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11×5
10÷2
(1+10)
=55
=(1+9)+(2+8)+(3+7)+(4+6)+5
=10+10+10+10+5
=9×5
10÷2
(1+9)
=50
=5×2+5×2+5×2+5×2+5
下面算式的和是多少,你能很快地计算出来吗?
1+2+3+4+5+…+100=( )
5050
2+3+4+5+…+18=( )
原式=(1+100)×(100-1+1)÷2=101×100÷2=
5050
原式=(2+18)×(18-2+1)÷2=20×17÷2
170
=170
从1开始的连续奇数的和正好是这列数个数的平方。
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
找规律
等比数列
×2
32
64
×2
×2
×2
×2
×2
×
×
×
×
×
×
8
16
24
照这样的规律接着画下去,
第5个图形最外圈有多少个小正方形?
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
=8
总个数:
3行3列
内圈个数:1行1列
第5个图形最外圈有多少个小正方形?
你能解释其中的道理吗?
32-12
52- 32
=8
总个数:5行5列
内圈个数:3行3列
32-12
52- 32
72- 52
=8
总个数:7行7列
内圈个数:5行5列
=16
=24
下面每个图中最外圈有多少个小正方形?
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去:
第6个图形有多少个绿色小正方形和多少个蓝色小正方形?
第10个图形呢?你能解释这其中的道理吗?
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
规律:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
1
8
2
10
3
12
4
14
绿色:
蓝色:
0
6
6+2×1
6+2×2
6+2×3
正方形总个数:蓝色小正方形的个数等于6加上红色小正方形个数的2倍。
第6个图形:
第10个图形:
6+2×6=18
6+2×10=26
6+2×4
6+2×0
2n+6
6. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第八个图形需要黑色棋子的个数是( )。
80
12+2×1
22+2×2
32+2×3
42+2×4
……
82+2×8
如下图,第一个图案用3根小棒,第二个图案用9根小棒,
那么第10个图案需要小棒___根。
(1+2)×3
(1+2+3)×3
(1+2+3+……10)×3
感 谢 聆 听
数学广角—数与形
人教版小学数学六年级上册
今日数学作业:
1.数学书106页1题、2题;107页1题、2题、3题,做数学书上,并将答案上传到小程序里;
2.一卷通三单元试卷全做,先将应用题和计算题、填空题上传到小程序,再根据答案自行改错,尽量用红笔改了。
网课反思:
1.下次全体成员必须更改备注名,好看到哪些同学进来听课;
2.网课的当天只会上1小时半的课时量,其余时间除了交作业(作业晚上交也可以),尽量让学生远离手机。
3.开学后不会重新再上网课教学内容,最多只是用几天时间复习下上期知识,每学期都有新的学业计划。
1+3=
1+3+5=
1+3+5+7=
1+3+5+7+9+…+15=
看谁算的快。
首尾相加
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
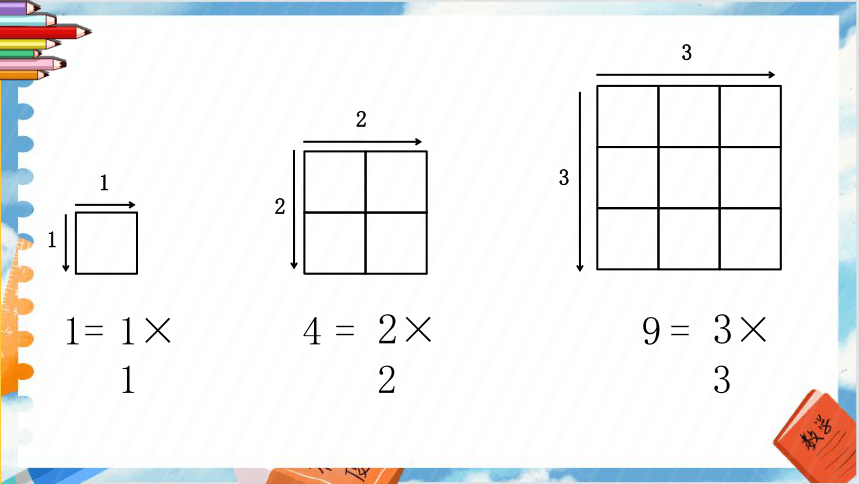
观察这三个算式,你有什么发现?
4
1
9
1
1
2
2
3
3
1×1
=
2×2
3×3
=
=
4
1
9
1
1
2
2
3
3
1×1
=
2×2
3×3
=
=
12
22
32
正方形数
有1个小正方形
每列或每行都有2个小正方形
每列或每行都有3个小正方形
4
1
9
=
=
=
12
22
32
1+3
1+3+5
3
5
1
1、3、5都是 奇数
连续的
1+3+5
32
=
1
=
12
1+3
=
22
从1开始,几个连续的奇数相加,就是几的平方。
1+3+5+……+(2n-1) = n2
n个连续奇数
上面这些图形的问题,需要考虑隐藏着数的规律来解决,这种方法我们称之为数形结合的方法。
数形结合是数学解题中常用的思想方法,数形结合的思想可以使某些抽象的数学问题直观化、生动化,能够变抽象思维为形象思维。
今天我们就一起来探索数形结合的奥妙!
图形
数与形
华罗庚
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
数字
利用规律直接写一写。
如果遇到困难,可以画图来帮助。
1+3+5+7=( )2
1+3+5+7+9+11+13 =( )2
1+3+5+7+9+11+13+15+17
4
7
______________________________=( 9 )2
易错点:只有从1开始的连续奇数相加的和才是平方数。
3个奇数
1. 请你根据例1的结论算一算。
1+3+5+7+5+3+1 =( )
25
1+3+5+7+9+11+13+11+9+7+5+3+1=( )
85
4个奇数
42
32
+
7个奇数
6个奇数
72
62
+
1. 观察图形,填写下表。
43
88
8+5×(n-1)
:按照规律接着画一画,填一填。
3
1
6
10
( )
( )
( )
如果不画,这样排列下去,第10个数是多少?
1+2+3+4+5+6+7+8+9+10=55
这些圆片都可以排成三角形,像这样的数称为三角形数
找规律
如图,摆一个三角形需要3根小棒,摆二个三角形需要5根小棒,摆10个三角形需要 根小棒。
1
三角形个数:
小棒数:
3
2
3+2
3
3+2+2
4
3+2+2+2
1+2×10
3+2×9
规律:
1+2
1+2+2
1+2+2+2
1+2+2+2+2
2×1+1
2×2+1
2×3+1
2×4+1
2×n+1
=2n+1
2. 先数一数,再填一填,用你发现的规律解决问题。
7
9
(1)摆15个三角形,需要多少根小棒?
31根
44个
摆成的三角形个数×2 +1 =所用的小棒根数
(2)有89根小棒,能摆出多少个三角形?
(3)摆成的三角形个数与所用的小棒根数之间有什么关系?
如图,用同样的小棒摆正方形,这样摆20个同样的正方形需要小棒___根
1
正方形个数:
小棒数:
4
2
4+3
3
4+3+3
1+3×20
4+3×19
……
5.下面每个三角形图各是由多少个小三角形组成的
如果小三角形的边长为1,每个三角形图的周长分别是多少
每个三角形图包含小三角形的个数与这个三角形图的周长之间有什么样的关系
你还能提出什么数学问题
1
3
4
6
9
9
16
12
请你根据上面图形与数的规律接着画一画,填一填。
如果不画,这样排列下去,第10个数是多少
15
21
28
第10个数是55
1+2+3+4+5
1+2+3+4+5+6
=(1+5)+(2+4)+3
=6+6+3
=3×2+3×2+3
=3×5
=(1+6)+(2+5)+(3+4)
=7+7+7
=7×3
6÷2
(1+6)
5
(1+5)
÷2
首项
末项
+
(
)
项数
×
÷2
等差数列:
相邻两个数之间的差相等
下面算式的和是多少,你能很快地计算出来吗?
1+2+3+4+5+…+10
1+2+2+3+4+5+…+9
=(1+10)+(2+9)+(3+8)+(4+7)+(5+6)
=11+11+11+11+11
=11×5
10÷2
(1+10)
=55
=(1+9)+(2+8)+(3+7)+(4+6)+5
=10+10+10+10+5
=9×5
10÷2
(1+9)
=50
=5×2+5×2+5×2+5×2+5
下面算式的和是多少,你能很快地计算出来吗?
1+2+3+4+5+…+100=( )
5050
2+3+4+5+…+18=( )
原式=(1+100)×(100-1+1)÷2=101×100÷2=
5050
原式=(2+18)×(18-2+1)÷2=20×17÷2
170
=170
从1开始的连续奇数的和正好是这列数个数的平方。
只要是1开始,连续的奇数相加,就能排成每行、每列个数是几的大正方形,和也就是几的平方。
找规律
等比数列
×2
32
64
×2
×2
×2
×2
×2
×
×
×
×
×
×
8
16
24
照这样的规律接着画下去,
第5个图形最外圈有多少个小正方形?
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
32-12
=8
总个数:
3行3列
内圈个数:1行1列
第5个图形最外圈有多少个小正方形?
你能解释其中的道理吗?
32-12
52- 32
=8
总个数:5行5列
内圈个数:3行3列
32-12
52- 32
72- 52
=8
总个数:7行7列
内圈个数:5行5列
=16
=24
下面每个图中最外圈有多少个小正方形?
32-12
=8
52- 32
=16
72- 52
=24
92- 72
=32
112- 92
=40
总个数:11行11列
内圈个数:9行9列
总个数:9行9列
内圈个数:7行7列
照这样的规律接着画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
下面每个图中最外圈有多少个小正方形?
照这样的规律接着画下去:
第6个图形有多少个绿色小正方形和多少个蓝色小正方形?
第10个图形呢?你能解释这其中的道理吗?
第6个图形:6个绿色18个蓝色。
第10个图形:10个绿色26个蓝色。
规律:任意两张相邻的图中,绿色相差1个,蓝色相差2个。
1
8
2
10
3
12
4
14
绿色:
蓝色:
0
6
6+2×1
6+2×2
6+2×3
正方形总个数:蓝色小正方形的个数等于6加上红色小正方形个数的2倍。
第6个图形:
第10个图形:
6+2×6=18
6+2×10=26
6+2×4
6+2×0
2n+6
6. 如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第八个图形需要黑色棋子的个数是( )。
80
12+2×1
22+2×2
32+2×3
42+2×4
……
82+2×8
如下图,第一个图案用3根小棒,第二个图案用9根小棒,
那么第10个图案需要小棒___根。
(1+2)×3
(1+2+3)×3
(1+2+3+……10)×3
感 谢 聆 听
