26.1 锐角三角函数练习

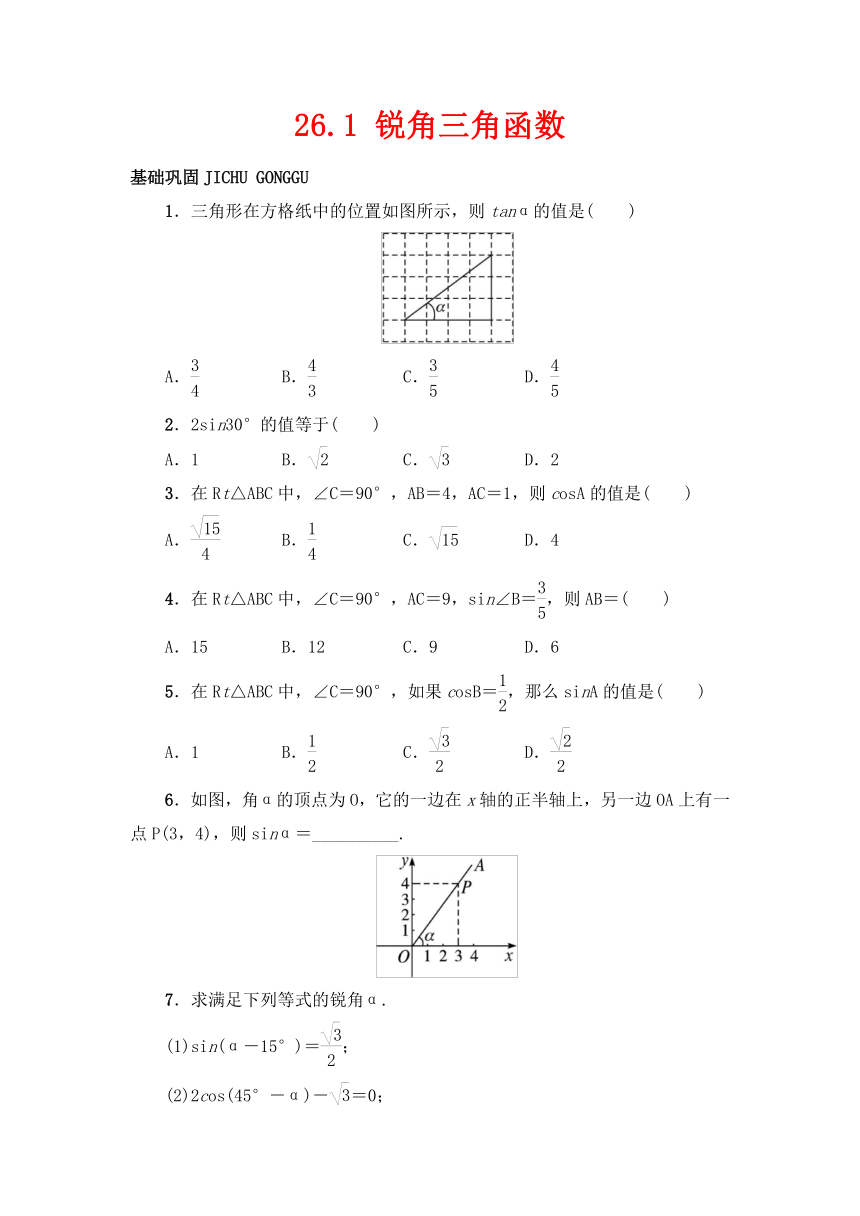
26.1 锐角三角函数
基础巩固JICHU GONGGU
1．三角形在方格纸中的位置如图所示，则tanα的值是(　　)
( http: / / www.21cnjy.com )
A． B． C． D．
2．2sin30°的值等于(　　)
A．1 B． C． D．2
3．在Rt△ABC中，∠C＝90°，AB＝4，AC＝1，则cosA的值是(　　)
A． B． C． D．4
4．在Rt△ABC中，∠C＝90°，AC＝9，sin∠B＝，则AB＝(　　)
A．15 B．12 C．9 D．6
5．在Rt△ABC中，∠C＝90°，如果cosB＝，那么sinA的值是(　　)
A．1 B． C． D．
6．如图，角α的顶点为O，它的一边在x轴的正半轴上，另一边OA上有一点P(3，4)，则sinα＝__________.
( http: / / www.21cnjy.com )
7．求满足下列等式的锐角α.
(1)sin(α－15°)＝；
(2)2cos(45°－α)－＝0；
(3)tan2α－4tanα＋＝0.
8．计算下列各题：
(1)cos30°cos45°＋cos60°；
(2) 2sin60°－2cos30°sin45°；
(3)；
(4)(cos45°－sin30°)＋(4－4π)0＋(－1)－1；
(5)sin30°＋cos260°－tan45°－tan30°.
能力提升NENGLI TISHENG
9．在△ABC中，∠C＝90°，sinA＝，则tanB＝(　　)
A． B． C． D．
10．如图，AD⊥CD，AB＝13，BC＝12，CD＝3，AD＝4，则tanB＝(　　)
( http: / / www.21cnjy.com )
A． B． C． D．
11．在Rt△ABC中，∠C＝90°，AB＝10，tanA＝，则BC的长是__________．
12．如图，在Rt△ABC中，∠ ACB＝90°，CD⊥AB于点D，已知AC＝，BC＝2，那么tan∠ACD＝__________.
( http: / / www.21cnjy.com )
13．设α为锐角，已知tanα＝，求sinα和cosα的值．
参考答案
1．A　2.A　3.B　4.A　5.B　6.
7．解：(1)75°；(2)15°；
(3)a＝，b＝－4，c＝，
∵b2－4ac＝42－4××＝4，
∴tanα＝
＝＝＝，
∴tanα1＝，tanα2＝，
∴α1＝60°，α2＝30°.
8．解：(1)原式＝×＋＝；
(2)原式＝2×－2××＝－；
(3)原式＝＝＝－1；
(4)原式＝(－)＋1＋(＋1)
＝1－＋1＋＋1＝3＋；
(5)原式＝＋－1－1＝－.
9．B　10.A
11．6　点拨：∵∠C＝90°，AB＝10，
∴AC＝＝.
∵tanA＝，即＝＝，
解得BC＝6.
12.　点拨：在Rt△ABC中，tan∠ABC＝＝；又因为∠ACD＝∠ABC，
所以tan∠ACD＝.
13．解：∵tanα＝，∴＝.
∴sinα＝cosα.
又∵sin2α＋cos2α＝1，∴＋cos2α＝1.
∵α为锐角，∴cosα＝，
∴sinα＝cosα＝×＝.