23.4 游戏的公平性(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 23.4 游戏的公平性(第1课时)(教学课件)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览







文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第 23章 概率初步
23.4 游戏的公平性(第1课时)
学习目标
1.会用画“树形图”的方法分析等可能试验中事件的概率问题, 并进行概率的计算. .(重点)
2.会用概率判断游戏的公平性.(难点)
情景引入
思考:当陨石落到地球上时,是落在陆地的可能性大,还是落入海洋的可能性大?试试利用概率的意义说明。
生活中有些可能性的大小与长度、面积或体积等有关,相关的概率问题可以通过有关度量计算来解决;
还有些概率问题可以利用图形来进行分析和研究,把问题转化再解决。
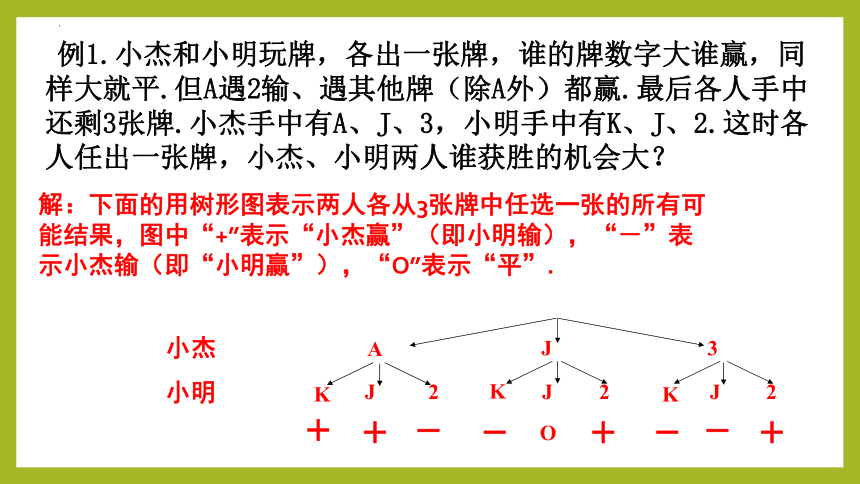
例1.小杰和小明玩牌,各出一张牌,谁的牌数字大谁赢,同样大就平.但A遇2输、遇其他牌(除A外)都赢.最后各人手中还剩3张牌.小杰手中有A、J、3,小明手中有K、J、2.这时各人任出一张牌,小杰、小明两人谁获胜的机会大?
解:下面的用树形图表示两人各从3张牌中任选一张的所有可能结果,图中“+”表示“小杰赢”(即小明输),“-”表示小杰输(即“小明赢”),“O”表示“平”.
K
J
2
K
J
2
K
J
2
小明
3
A
J
小杰
╋
╋
━
━
O
╋
━
━
╋
从图中可以看出,两人各从3张牌中任出一张牌,共有9个等可能结果.
设事件A:”小杰赢”; 事件B:”小明赢”.
事件A包含其中的四种结果:
(A,K)、(A,J)、(J,2)、(3,2);
事件B也包含其中的四种结果:
(A,2)、(J,K)、(3,K)、(3,J)
所以,P(A)=P(B)=
,即两人获胜的机会一样大.
例2.甲、乙、丙三个球迷只有一张球票,要通过抓阄决定谁去看球.为此,准备了三张纸片,其中有一张画了个圆圈“O”,抓中的人得到球票;另两张纸片空白.抓阄前,甲提出要先抓,他想先抓的人得到球票的机会大.他的想法对吗?
注意:抓阄是不放回地取纸片,因此先后抓阄的试验不是相同条件下的重复试验,但以全过程为分步完成的一次试验则它是等可能试验
解:假设抓阄的顺序依次是甲、乙、丙.3张纸片中一张画“O”,我们用“O”表示抓中,其余用“白1”、白2“表示,用树形图展示所有可能的结果如下:
白2
白2
白1
白1
O
O
丙
白1
O
O
白1
白2
白2
乙
O
白1
白2
甲
从图中可以看出,共有6种可能的结果,其中甲、乙、丙抓到画“O”的纸片的结果各有2种,可知概率都是????????,所以他们得到球票的机会一样大.
?
甲 O 甲 O 乙 O 丙 O 乙 O 丙 O
1.一人把分别写有“20”“10”“世博”的 3 张相同卡片,字面朝下随意放在桌面上;另一人再把这 3 张卡片排成一行,从左到右恰好排成“2010 世博”或者“世博 2010”的概率是( )
2.从 2,6,8 这三个数中任选两个组成两位数,在组成的所有两位数中任意抽取一个数,这个数恰好能被 4 整除的概率是多少?
课本练习
3.三位同伴进饭店用餐,把每人自带的雨伞交给服务员放在一起保管,离店时服务员把他们的雨伞随意还给各人,三位同伴恰好拿到各自雨伞的概率是多少?各自都没有拿到自己的雨伞的概率是多少?你觉得这两件事哪个发生的可能性更大呢?
1
2
甲
3
乙
2
3
1
3
1
2
丙
3
2
3
1
2
1
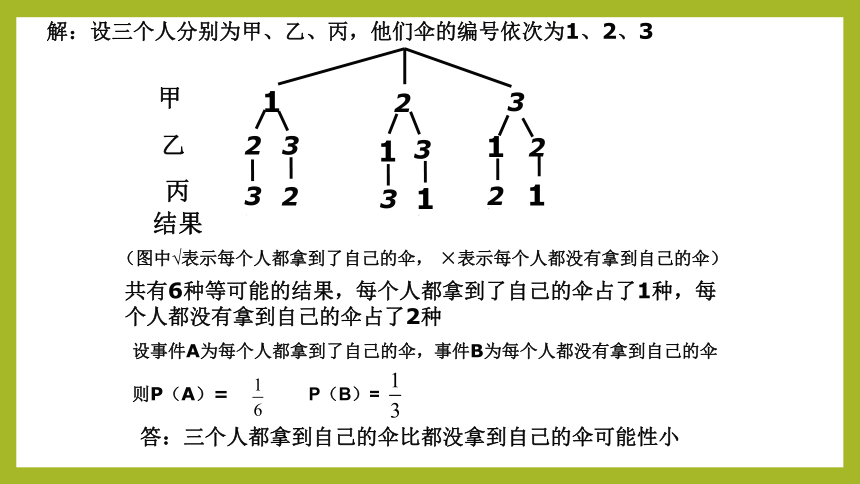
答:三个人都拿到自己的伞比都没拿到自己的伞可能性小
结果
共有6种等可能的结果,每个人都拿到了自己的伞占了1种,每个人都没有拿到自己的伞占了2种
(图中√表示每个人都拿到了自己的伞, ×表示每个人都没有拿到自己的伞)
设事件A为每个人都拿到了自己的伞,事件B为每个人都没有拿到自己的伞
则P(A)= P(B)=
√
×
×
解:设三个人分别为甲、乙、丙,他们伞的编号依次为1、2、3
随堂检测
3.从下列四张牌中随机抽两张,抽中同种花色的概率是多少?
解:设A、A、 2 、2,分别被记为A1、A2、B1、B2,则
B1
A1
B2
A2
A2
B1
B2
A1
B1
B2
A1
A2
B2
A1
A2
B1
设事件A:“抽到同色牌”,则
(图中√表示随机摸两个球摸到同色)
√
√
√
√
共有12种等可能情况,抽到同色牌的有4种情况
答:抽到同色牌的概率是
4、搞抽奖活动,布袋里有5个颜色不同的小球,其中红球、黄球、绿球各1个, 黑球2个.奖品的情况如图所示。
(1)摸出1个球,摸不到奖的概率是多少?
(2)同时摸2个球,获得的奖品价值超过10元的概率是多少?
50元的奖品
20元的奖品
10元的奖品
无奖品
红球
黄球
绿球
黑球
(2)将球按奖品价值排列:50,20,10,0,0任取2个的等可能结果有:(50 20)(5 0 10)(50 0)(50 0)(20 10)(20 0)(20 0)(10 0)(10 0)(0 0)共10种结果,超过10元有7种结果,所以P(超过10元)= .
5.小明给小杰出道题:从点数为1到4的四张牌中任意抽两张,求两张牌的点数之和等于5的概率.
小杰用列表法展示抽两张牌可能取得的所有16种结果。如表所示,两张牌的点数之和为5,有(1,4)(2,3)(3,2)(4,1)共4种可能,因此抽到2张牌的点数为5的概率是 .
你能求出两张牌的点数互素的概率吗?
1
2
3
4
1
(1,1)
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,3)
(3,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
两点数非互素有(2,2)(2,4)(3,3)(4,2)(4,4)共5种结果,故两点数互素有11种结果,所以两张牌的点数互素概率为
6. 甲乙两人玩骰子,他们各自掷一枚骰子,想对掷出的两个数进行某种运算,再根据运算的结果来定胜负。但进行什么样的运算才公平,两人争论不休。后来他们提出了下面两个方案:
(1)两数之和等于8时甲胜,两数之和等于9时乙胜;
(2)两数和大于8时甲胜,大数减小数的差小于2时乙胜。
请你用上题所用的列表法分析这两个游戏规则的方案。这样的游戏规则公平吗?如果不公平,试修改相应的规则,使游戏变得公平。
(1 1)
(1 2)
(1 3)
(1 4)
(1 5)
(1 6)
(2 1)
(2 2)
(2 3)
(2 4)
(2 5)
(2 6)
(3 1)
(3 2)
(3 3)
(3 4)
(3 5)
(3 6)
(4 1)
(4 2)
(4 3)
(4 4)
(4 5)
(4 6)
(5 1)
(5 2)
(5 3)
(5 4)
(5 5)
(5 6)
(6 1)
(6 2)
(6 3)
(6 4)
(6 5)
(6 6)
掷两枚骰子共有36个等可能结果,“两数和为8”有5种结果,“两数和为9”有4种结果; “两数和大于8”有10种结果,“大数减小数的差小于2”有 (1 1)(2 2)(3 3)(4 4)(5 5)(6 6)(1 2)(2 3)(3 4)(4 5)(5 6)(2 1)(3 2)(4 3)(5 4)(6 5)共16种结果,故方案① ②都不公平。
公平游戏规则有很多,如①两数之和等于8时甲胜,两数之和等于6则乙胜。②大数减小数的差等于0时甲胜,差大于3则乙胜.
7.小明和小慧玩纸牌游戏. 图 是同一副扑克牌中4 张牌的正面,将它们正面朝下洗匀后放在桌上,小明先从中抽出1 张,小慧从剩余的3 张牌中也抽出1 张(扑克牌Q 代表12).
小慧说:“若抽出的两张牌的数字都是偶数,小明获胜;否则,我获胜.”
(1)请用画树形图的方法表示两人抽牌可能出现的所有结果.
(2)若按小慧说的规则进行游戏,这个游戏公平吗?请说明理由.
解:(1)画树形图如图所示,共有12 种等可能的结果.
(2)游戏公平.
理由:因为小慧获胜的概率P(小慧获胜)= 12 ,
小明获胜的概率P(小明获胜)= 12 ,
P(小慧获胜)= P(小明获胜),
所以游戏公平.
课堂小结
1.可以利用图形的面积关系来计算事件的概率;
2.可以采用列举、树形图、坐标系等方法列出所有的等可能结果。
3.怎样利用概率判断游戏是否公平?
如果两方获胜的概率相等,那么游戏公平,否则游戏不公平.
第 23章 概率初步
23.4 游戏的公平性(第1课时)
学习目标
1.会用画“树形图”的方法分析等可能试验中事件的概率问题, 并进行概率的计算. .(重点)
2.会用概率判断游戏的公平性.(难点)
情景引入
思考:当陨石落到地球上时,是落在陆地的可能性大,还是落入海洋的可能性大?试试利用概率的意义说明。
生活中有些可能性的大小与长度、面积或体积等有关,相关的概率问题可以通过有关度量计算来解决;
还有些概率问题可以利用图形来进行分析和研究,把问题转化再解决。
例1.小杰和小明玩牌,各出一张牌,谁的牌数字大谁赢,同样大就平.但A遇2输、遇其他牌(除A外)都赢.最后各人手中还剩3张牌.小杰手中有A、J、3,小明手中有K、J、2.这时各人任出一张牌,小杰、小明两人谁获胜的机会大?
解:下面的用树形图表示两人各从3张牌中任选一张的所有可能结果,图中“+”表示“小杰赢”(即小明输),“-”表示小杰输(即“小明赢”),“O”表示“平”.
K
J
2
K
J
2
K
J
2
小明
3
A
J
小杰
╋
╋
━
━
O
╋
━
━
╋
从图中可以看出,两人各从3张牌中任出一张牌,共有9个等可能结果.
设事件A:”小杰赢”; 事件B:”小明赢”.
事件A包含其中的四种结果:
(A,K)、(A,J)、(J,2)、(3,2);
事件B也包含其中的四种结果:
(A,2)、(J,K)、(3,K)、(3,J)
所以,P(A)=P(B)=
,即两人获胜的机会一样大.
例2.甲、乙、丙三个球迷只有一张球票,要通过抓阄决定谁去看球.为此,准备了三张纸片,其中有一张画了个圆圈“O”,抓中的人得到球票;另两张纸片空白.抓阄前,甲提出要先抓,他想先抓的人得到球票的机会大.他的想法对吗?
注意:抓阄是不放回地取纸片,因此先后抓阄的试验不是相同条件下的重复试验,但以全过程为分步完成的一次试验则它是等可能试验
解:假设抓阄的顺序依次是甲、乙、丙.3张纸片中一张画“O”,我们用“O”表示抓中,其余用“白1”、白2“表示,用树形图展示所有可能的结果如下:
白2
白2
白1
白1
O
O
丙
白1
O
O
白1
白2
白2
乙
O
白1
白2
甲
从图中可以看出,共有6种可能的结果,其中甲、乙、丙抓到画“O”的纸片的结果各有2种,可知概率都是????????,所以他们得到球票的机会一样大.
?
甲 O 甲 O 乙 O 丙 O 乙 O 丙 O
1.一人把分别写有“20”“10”“世博”的 3 张相同卡片,字面朝下随意放在桌面上;另一人再把这 3 张卡片排成一行,从左到右恰好排成“2010 世博”或者“世博 2010”的概率是( )
2.从 2,6,8 这三个数中任选两个组成两位数,在组成的所有两位数中任意抽取一个数,这个数恰好能被 4 整除的概率是多少?
课本练习
3.三位同伴进饭店用餐,把每人自带的雨伞交给服务员放在一起保管,离店时服务员把他们的雨伞随意还给各人,三位同伴恰好拿到各自雨伞的概率是多少?各自都没有拿到自己的雨伞的概率是多少?你觉得这两件事哪个发生的可能性更大呢?
1
2
甲
3
乙
2
3
1
3
1
2
丙
3
2
3
1
2
1
答:三个人都拿到自己的伞比都没拿到自己的伞可能性小
结果
共有6种等可能的结果,每个人都拿到了自己的伞占了1种,每个人都没有拿到自己的伞占了2种
(图中√表示每个人都拿到了自己的伞, ×表示每个人都没有拿到自己的伞)
设事件A为每个人都拿到了自己的伞,事件B为每个人都没有拿到自己的伞
则P(A)= P(B)=
√
×
×
解:设三个人分别为甲、乙、丙,他们伞的编号依次为1、2、3
随堂检测
3.从下列四张牌中随机抽两张,抽中同种花色的概率是多少?
解:设A、A、 2 、2,分别被记为A1、A2、B1、B2,则
B1
A1
B2
A2
A2
B1
B2
A1
B1
B2
A1
A2
B2
A1
A2
B1
设事件A:“抽到同色牌”,则
(图中√表示随机摸两个球摸到同色)
√
√
√
√
共有12种等可能情况,抽到同色牌的有4种情况
答:抽到同色牌的概率是
4、搞抽奖活动,布袋里有5个颜色不同的小球,其中红球、黄球、绿球各1个, 黑球2个.奖品的情况如图所示。
(1)摸出1个球,摸不到奖的概率是多少?
(2)同时摸2个球,获得的奖品价值超过10元的概率是多少?
50元的奖品
20元的奖品
10元的奖品
无奖品
红球
黄球
绿球
黑球
(2)将球按奖品价值排列:50,20,10,0,0任取2个的等可能结果有:(50 20)(5 0 10)(50 0)(50 0)(20 10)(20 0)(20 0)(10 0)(10 0)(0 0)共10种结果,超过10元有7种结果,所以P(超过10元)= .
5.小明给小杰出道题:从点数为1到4的四张牌中任意抽两张,求两张牌的点数之和等于5的概率.
小杰用列表法展示抽两张牌可能取得的所有16种结果。如表所示,两张牌的点数之和为5,有(1,4)(2,3)(3,2)(4,1)共4种可能,因此抽到2张牌的点数为5的概率是 .
你能求出两张牌的点数互素的概率吗?
1
2
3
4
1
(1,1)
(1,2)
(1,3)
(1,4)
2
(2,1)
(2,2)
(2,3)
(2,4)
3
(3,1)
(3,2)
(3,3)
(3,4)
4
(4,1)
(4,2)
(4,3)
(4,4)
两点数非互素有(2,2)(2,4)(3,3)(4,2)(4,4)共5种结果,故两点数互素有11种结果,所以两张牌的点数互素概率为
6. 甲乙两人玩骰子,他们各自掷一枚骰子,想对掷出的两个数进行某种运算,再根据运算的结果来定胜负。但进行什么样的运算才公平,两人争论不休。后来他们提出了下面两个方案:
(1)两数之和等于8时甲胜,两数之和等于9时乙胜;
(2)两数和大于8时甲胜,大数减小数的差小于2时乙胜。
请你用上题所用的列表法分析这两个游戏规则的方案。这样的游戏规则公平吗?如果不公平,试修改相应的规则,使游戏变得公平。
(1 1)
(1 2)
(1 3)
(1 4)
(1 5)
(1 6)
(2 1)
(2 2)
(2 3)
(2 4)
(2 5)
(2 6)
(3 1)
(3 2)
(3 3)
(3 4)
(3 5)
(3 6)
(4 1)
(4 2)
(4 3)
(4 4)
(4 5)
(4 6)
(5 1)
(5 2)
(5 3)
(5 4)
(5 5)
(5 6)
(6 1)
(6 2)
(6 3)
(6 4)
(6 5)
(6 6)
掷两枚骰子共有36个等可能结果,“两数和为8”有5种结果,“两数和为9”有4种结果; “两数和大于8”有10种结果,“大数减小数的差小于2”有 (1 1)(2 2)(3 3)(4 4)(5 5)(6 6)(1 2)(2 3)(3 4)(4 5)(5 6)(2 1)(3 2)(4 3)(5 4)(6 5)共16种结果,故方案① ②都不公平。
公平游戏规则有很多,如①两数之和等于8时甲胜,两数之和等于6则乙胜。②大数减小数的差等于0时甲胜,差大于3则乙胜.
7.小明和小慧玩纸牌游戏. 图 是同一副扑克牌中4 张牌的正面,将它们正面朝下洗匀后放在桌上,小明先从中抽出1 张,小慧从剩余的3 张牌中也抽出1 张(扑克牌Q 代表12).
小慧说:“若抽出的两张牌的数字都是偶数,小明获胜;否则,我获胜.”
(1)请用画树形图的方法表示两人抽牌可能出现的所有结果.
(2)若按小慧说的规则进行游戏,这个游戏公平吗?请说明理由.
解:(1)画树形图如图所示,共有12 种等可能的结果.
(2)游戏公平.
理由:因为小慧获胜的概率P(小慧获胜)= 12 ,
小明获胜的概率P(小明获胜)= 12 ,
P(小慧获胜)= P(小明获胜),
所以游戏公平.
课堂小结
1.可以利用图形的面积关系来计算事件的概率;
2.可以采用列举、树形图、坐标系等方法列出所有的等可能结果。
3.怎样利用概率判断游戏是否公平?
如果两方获胜的概率相等,那么游戏公平,否则游戏不公平.
