20.2.1方差(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 20.2.1方差(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 14:05:59 | ||
图片预览







文档简介
(共21张PPT)
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.2.1
方差
情景引入
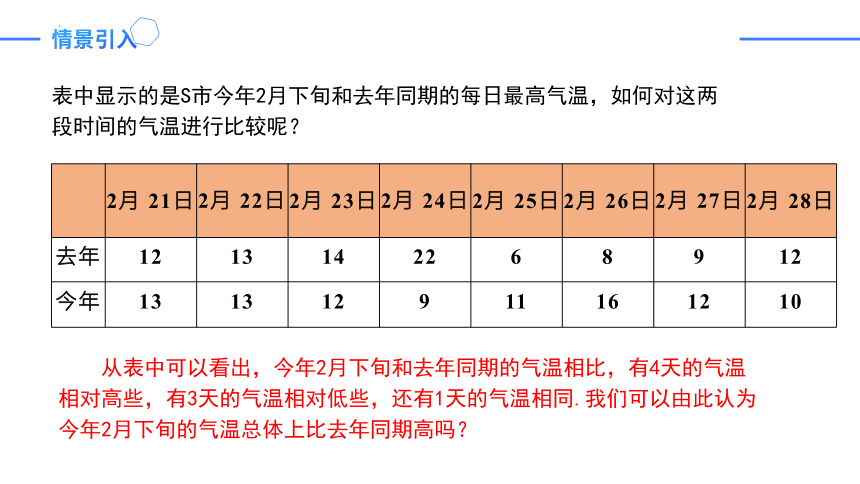
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月 28日
去年 12 13 14 22 6 8 9 12
今年 13 13 12 9 11 16 12 10
表中显示的是S市今年2月下旬和去年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
从表中可以看出,今年2月下旬和去年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为今年2月下旬的气温总体上比去年同期高吗?
情景引入
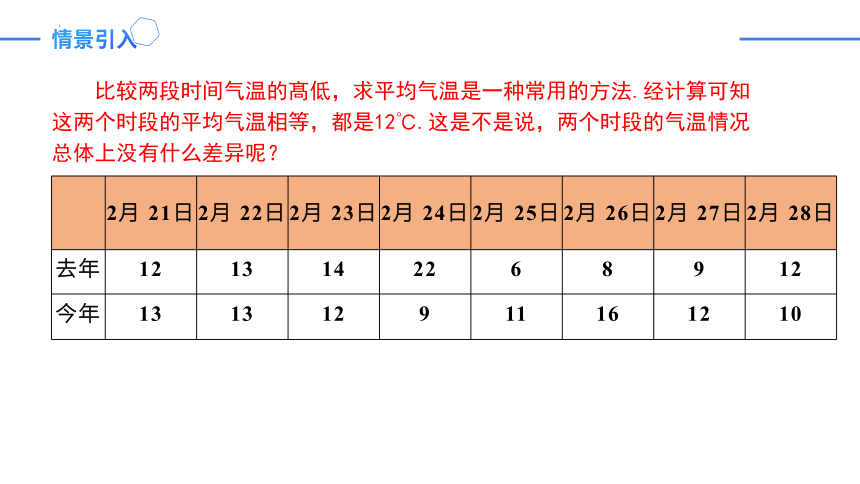
比较两段时间气温的髙低,求平均气温是一种常用的方法.经计算可知这两个时段的平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月 28日
去年 12 13 14 22 6 8 9 12
今年 13 13 12 9 11 16 12 10
新知探究
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现:
去年的点波动范围比较大——
从6℃到22℃,今年的点波动范围比较小——从9℃到16℃;
去年气温的最大值与最小值之间差距很大,相差16℃;
今年气温的最大值与最小值相差7℃,
总体上气温变化的范围不太大.
方差
新知探究
1.方差的概念:
设有n个数据x1,x2,…,xn,各数据与它们的平均数
的差的平方分别是 ,
我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫做这组数据的方差.
方差
新知探究
2.方差的意义
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小).
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例1
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下: =80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例2
一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
根据平均数的计算公式先求出a的值,再根据方差公式
s2= 代数计算即可.
∵6、4、a、3、2的平均数是5,
∴(6+4+a+3+2)÷5=5,
解得a=10,
则这组数据的方差
s2= ×[(6-5)2+(4-5)2+(10-5)2+(3-5)2+(2-5)2]=8.
A
典例精析
例3
某特警部队为了选拔“神枪手”,举行了1 000米射击比赛,最后由甲、乙两名战士进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.11,则下列说法中,正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人成绩的稳定性相同
D.无法确定谁的成绩更稳定
B
典例精析
例4
为了考察甲、乙两种小麦的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
哪种麦苗长势整齐?
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
典例精析
例4
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
典例精析
例5
检查人员从两家的食品加工厂的原料包中各随机抽取15 袋,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为食品公司应该选购哪家加工厂的原料包?
解:样本数据的平均数分别是:
样本平均数相同,
估计这批原料包的
平均质量相近.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
典例精析
例5
解:样本数据的方差分别是:
由 可知,两家加工厂的原料包质量大致相等;
由 < 可知,甲加工厂的原料包质量更稳定,大小更均匀.
因此,食品公司应该选购甲加工厂生产的原料包.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
归纳总结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
当堂检测
1.两名同学各进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的
( )
A.众数 B.中位数
C.方差 D.以上都不对
2.在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是s甲2=0.35,s乙2=0.15,s丙2=0.25,s丁2=0.27,这4人中成绩发挥最稳定的是( )
A.甲 B.乙
C.丙 D.丁
C
B
当堂检测
3.工厂欲招收一名技工,下表是对两名应聘者加工相同数量同一种零件的数据进行分析所得的结果,你认为录用哪位较好?( )
A.录用甲 B.录用乙
C.录用甲、乙都一样 D.无法判断录用甲、乙
平均数 方差
甲 80 269
乙 80 86
B
4.如果将一组数据中的每一个数据都加上一个非零常数,那么这组数据的( )
A.平均数和方差都不变 B.平均数不变,方差改变
C.平均数改变,方差不变 D.平均数和方差都改变
C
当堂检测
5.在某中学举行的演讲比赛中,初一年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93
选 手 1 号 2 号 3 号 4 号 5 号 平均
成绩
得分 90 95 █ 89 88 91
B
当堂检测
6.在今年我市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错的是( )
A.平均数为160 B.中位数为158
C.众数为158 D.方差为20.3
D
当堂检测
7.在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①s甲2>s乙2;②s甲2A.①③
B.①④
C.②③
D.②④
C
当堂检测
8.在样本方差的计算公式
中, 数字10 表示___________ ,数字20表示 _______.
样本容量
平均数
9.五个数1,3,a,5,8的平均数是4,则a =_____,
这五个数的方差_____.
3
5.6
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.2.1
方差
情景引入
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月 28日
去年 12 13 14 22 6 8 9 12
今年 13 13 12 9 11 16 12 10
表中显示的是S市今年2月下旬和去年同期的每日最高气温,如何对这两段时间的气温进行比较呢?
从表中可以看出,今年2月下旬和去年同期的气温相比,有4天的气温相对高些,有3天的气温相对低些,还有1天的气温相同.我们可以由此认为今年2月下旬的气温总体上比去年同期高吗?
情景引入
比较两段时间气温的髙低,求平均气温是一种常用的方法.经计算可知这两个时段的平均气温相等,都是12℃.这是不是说,两个时段的气温情况总体上没有什么差异呢?
2月 21日 2月 22日 2月 23日 2月 24日 2月 25日 2月 26日 2月 27日 2月 28日
去年 12 13 14 22 6 8 9 12
今年 13 13 12 9 11 16 12 10
新知探究
观察下图,你感觉它们有没有差异呢?
通过观察,我们可以发现:
去年的点波动范围比较大——
从6℃到22℃,今年的点波动范围比较小——从9℃到16℃;
去年气温的最大值与最小值之间差距很大,相差16℃;
今年气温的最大值与最小值相差7℃,
总体上气温变化的范围不太大.
方差
新知探究
1.方差的概念:
设有n个数据x1,x2,…,xn,各数据与它们的平均数
的差的平方分别是 ,
我们用这些值的平均数,即
来衡量这组数据的波动大小,并把它叫做这组数据的方差.
方差
新知探究
2.方差的意义
方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小).
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例1
人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下: =80,s2甲=240,s2乙=180,则成绩较为稳定的班级是( )
A.甲班 B.乙班
C.两班成绩一样稳定 D.无法确定
B
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例2
一组数据6、4、a、3、2的平均数是5,这组数据的方差为( )
A.8 B.5 C.2 D.3
根据平均数的计算公式先求出a的值,再根据方差公式
s2= 代数计算即可.
∵6、4、a、3、2的平均数是5,
∴(6+4+a+3+2)÷5=5,
解得a=10,
则这组数据的方差
s2= ×[(6-5)2+(4-5)2+(10-5)2+(3-5)2+(2-5)2]=8.
A
典例精析
例3
某特警部队为了选拔“神枪手”,举行了1 000米射击比赛,最后由甲、乙两名战士进入决赛,在相同条件下,两人各射靶10次,经过统计计算,甲、乙两名战士的总成绩都是99.68环,甲的方差是0.28,乙的方差是0.11,则下列说法中,正确的是( )
A.甲的成绩比乙的成绩稳定
B.乙的成绩比甲的成绩稳定
C.甲、乙两人成绩的稳定性相同
D.无法确定谁的成绩更稳定
B
典例精析
例4
为了考察甲、乙两种小麦的长势,分别从中抽取了10株麦苗,测得高度(单位:cm)如下:
哪种麦苗长势整齐?
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
典例精析
例4
x甲= ×(15+15+…+15)=13.9(cm),
s甲2= ×[(15-13.9)2+(15-13.9)2+…+(15-13.9)2]
=2.09,
x乙= ×(17+14+…+11)=14(cm),
s乙2= ×[(17-14)2+(14-14)2+…+(11-14)2]=2.8,
因为s甲2<s乙2,所以甲种麦苗长势整齐.
解:
-
-
甲:15,15,14,11,16,14,12,14,13,15;
乙:17,14,12,16,15,14,14,14,13,11.
典例精析
例5
检查人员从两家的食品加工厂的原料包中各随机抽取15 袋,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为食品公司应该选购哪家加工厂的原料包?
解:样本数据的平均数分别是:
样本平均数相同,
估计这批原料包的
平均质量相近.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
典例精析
例5
解:样本数据的方差分别是:
由 可知,两家加工厂的原料包质量大致相等;
由 < 可知,甲加工厂的原料包质量更稳定,大小更均匀.
因此,食品公司应该选购甲加工厂生产的原料包.
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
归纳总结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
当堂检测
1.两名同学各进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的
( )
A.众数 B.中位数
C.方差 D.以上都不对
2.在某次射击训练中,甲、乙、丙、丁4人各射击10次,平均成绩相同,方差分别是s甲2=0.35,s乙2=0.15,s丙2=0.25,s丁2=0.27,这4人中成绩发挥最稳定的是( )
A.甲 B.乙
C.丙 D.丁
C
B
当堂检测
3.工厂欲招收一名技工,下表是对两名应聘者加工相同数量同一种零件的数据进行分析所得的结果,你认为录用哪位较好?( )
A.录用甲 B.录用乙
C.录用甲、乙都一样 D.无法判断录用甲、乙
平均数 方差
甲 80 269
乙 80 86
B
4.如果将一组数据中的每一个数据都加上一个非零常数,那么这组数据的( )
A.平均数和方差都不变 B.平均数不变,方差改变
C.平均数改变,方差不变 D.平均数和方差都改变
C
当堂检测
5.在某中学举行的演讲比赛中,初一年级5名参赛选手的成绩如下表所示,请你根据表中提供的数据,计算出这5名选手成绩的方差是( )
A. 2 B.6.8
C.34 D.93
选 手 1 号 2 号 3 号 4 号 5 号 平均
成绩
得分 90 95 █ 89 88 91
B
当堂检测
6.在今年我市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错的是( )
A.平均数为160 B.中位数为158
C.众数为158 D.方差为20.3
D
当堂检测
7.在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①s甲2>s乙2;②s甲2
B.①④
C.②③
D.②④
C
当堂检测
8.在样本方差的计算公式
中, 数字10 表示___________ ,数字20表示 _______.
样本容量
平均数
9.五个数1,3,a,5,8的平均数是4,则a =_____,
这五个数的方差_____.
3
5.6
