20.2.2根据方差做决策 课件(共14张PPT)
文档属性
| 名称 | 20.2.2根据方差做决策 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 20:49:17 | ||
图片预览





文档简介
(共14张PPT)
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.2.2
根据方差做决策
情景引入
李大叔几年前承包了甲、乙两片荒山,各栽了150棵荔枝,成活率约90%.现已挂果准备采收.为了分析收成情况,他从两山上各选了4棵树采摘入库,每棵树荔枝的产量如下折线统计图所示.
通过折线统计图提供的信息,我们可以分别计算甲、乙两山样本的平均数,并根据样本的平均数估计出甲、乙两山荔枝的产量总和,如果李大叔还想知道哪个荒山上荔枝的产量比较稳定,那么又该怎么办?同学们能否帮助李大叔解决这个问题?
复习回顾
方差的计算公式,请举例说明方差的意义.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例1
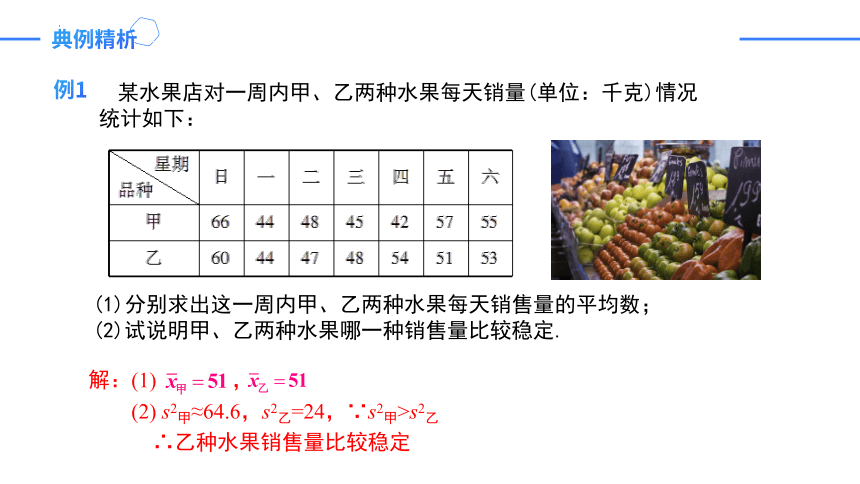
某水果店对一周内甲、乙两种水果每天销量(单位:千克)情况统计如下:
(1)分别求出这一周内甲、乙两种水果每天销售量的平均数;
(2)试说明甲、乙两种水果哪一种销售量比较稳定.
解:(1) ,
(2) s2甲≈64.6,s2乙=24,∵s2甲>s2乙
∴乙种水果销售量比较稳定
典例精析
例2
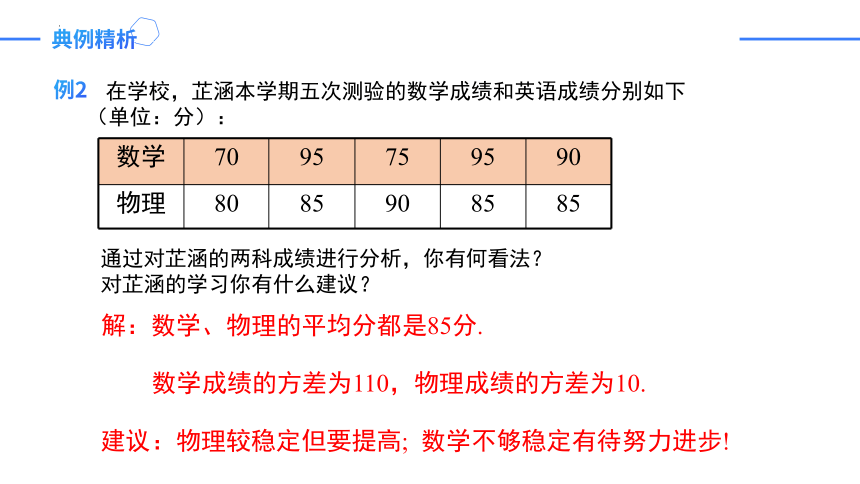
在学校,芷涵本学期五次测验的数学成绩和英语成绩分别如下(单位:分):
数学 70 95 75 95 90
物理 80 85 90 85 85
通过对芷涵的两科成绩进行分析,你有何看法?
对芷涵的学习你有什么建议?
解:数学、物理的平均分都是85分.
数学成绩的方差为110,物理成绩的方差为10.
建议:物理较稳定但要提高; 数学不够稳定有待努力进步!
典例精析
例3
某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
解:甲进球的平均数为 =8,方差为 .
(1)求甲、乙进球的平均数和方差;
典例精析
例3
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
典例精析
例1
甲乙两名工人平均每天加工的零件个数如下表所示,公司将举办职工技能大赛,如果你是经理,考虑比赛的结果,你将会派谁去参加比赛?
解:甲乙加工零件个数的平均数分别是:
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
典例精析
解:甲乙加工零件个数的方差分别是:
由 可知,甲乙加工零件个数大致相等;
由 < 可知,甲加工零件个数更稳定,因此,派甲去参加比赛会更合适.
归纳总结
根据方差做决策
方差的作用:比较数据的稳定性
利用样本方差估计总体方差
当堂检测
1.甲、乙两班各有8名学生参加数学竞赛,成绩如下表:
甲 65 74 70 80 65 66 69 71
乙 60 75 78 61 80 62 65 79
请比较两班学生成绩的优劣.
当堂检测
当堂检测
2.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛.在最近10次选拔赛中,他们的成绩(单位: cm)如下:
(1)这两名运动员的运动成绩各有何特点?
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
解:
(585+596+610+598+612+597+604+600+613+601)=601.6,s2甲≈65.84;
(613+618+580+574+618+593+585+590+598+624)=599.3,s2乙≈284.21.
由上面计算结果可知:甲队员的平均成绩较好,也比较稳定,乙队员的成绩相对不稳定.但甲队员的成绩不突出,乙队员和甲队员相比比较突出.
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.2.2
根据方差做决策
情景引入
李大叔几年前承包了甲、乙两片荒山,各栽了150棵荔枝,成活率约90%.现已挂果准备采收.为了分析收成情况,他从两山上各选了4棵树采摘入库,每棵树荔枝的产量如下折线统计图所示.
通过折线统计图提供的信息,我们可以分别计算甲、乙两山样本的平均数,并根据样本的平均数估计出甲、乙两山荔枝的产量总和,如果李大叔还想知道哪个荒山上荔枝的产量比较稳定,那么又该怎么办?同学们能否帮助李大叔解决这个问题?
复习回顾
方差的计算公式,请举例说明方差的意义.
方差的适用条件:
当两组数据的平均数相等或相近时,才利用方差来判断它们的波动情况.
方差越大,数据的波动越大;
方差越小,数据的波动越小.
典例精析
例1
某水果店对一周内甲、乙两种水果每天销量(单位:千克)情况统计如下:
(1)分别求出这一周内甲、乙两种水果每天销售量的平均数;
(2)试说明甲、乙两种水果哪一种销售量比较稳定.
解:(1) ,
(2) s2甲≈64.6,s2乙=24,∵s2甲>s2乙
∴乙种水果销售量比较稳定
典例精析
例2
在学校,芷涵本学期五次测验的数学成绩和英语成绩分别如下(单位:分):
数学 70 95 75 95 90
物理 80 85 90 85 85
通过对芷涵的两科成绩进行分析,你有何看法?
对芷涵的学习你有什么建议?
解:数学、物理的平均分都是85分.
数学成绩的方差为110,物理成绩的方差为10.
建议:物理较稳定但要提高; 数学不够稳定有待努力进步!
典例精析
例3
某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
解:甲进球的平均数为 =8,方差为 .
(1)求甲、乙进球的平均数和方差;
典例精析
例3
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
队员 每人每天进球数 甲 10 6 10 6 8
乙 7 9 7 8 9
典例精析
例1
甲乙两名工人平均每天加工的零件个数如下表所示,公司将举办职工技能大赛,如果你是经理,考虑比赛的结果,你将会派谁去参加比赛?
解:甲乙加工零件个数的平均数分别是:
甲
74
74
75
74
76
73
76
73
76
75
78
77
74
72
73
乙
75
73
79
72
76
71
73
72
78
74
77
78
80
71
75
典例精析
解:甲乙加工零件个数的方差分别是:
由 可知,甲乙加工零件个数大致相等;
由 < 可知,甲加工零件个数更稳定,因此,派甲去参加比赛会更合适.
归纳总结
根据方差做决策
方差的作用:比较数据的稳定性
利用样本方差估计总体方差
当堂检测
1.甲、乙两班各有8名学生参加数学竞赛,成绩如下表:
甲 65 74 70 80 65 66 69 71
乙 60 75 78 61 80 62 65 79
请比较两班学生成绩的优劣.
当堂检测
当堂检测
2.某校要从甲、乙两名跳远运动员中挑选一人参加一项校际比赛.在最近10次选拔赛中,他们的成绩(单位: cm)如下:
(1)这两名运动员的运动成绩各有何特点?
甲:585 596 610 598 612 597 604 600 613 601
乙:613 618 580 574 618 593 585 590 598 624
解:
(585+596+610+598+612+597+604+600+613+601)=601.6,s2甲≈65.84;
(613+618+580+574+618+593+585+590+598+624)=599.3,s2乙≈284.21.
由上面计算结果可知:甲队员的平均成绩较好,也比较稳定,乙队员的成绩相对不稳定.但甲队员的成绩不突出,乙队员和甲队员相比比较突出.
