第十二章 二次根式(小结与思考) 单元复习课件(共42张PPT)
文档属性
| 名称 | 第十二章 二次根式(小结与思考) 单元复习课件(共42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
第12章 二次根式
小结与思考
学习目标
1.整理、总结二次根式的相关知识,在巩固基本知识的基础上学会灵活运用;
2.感受化归的数学思想,提高探究问题的能力.
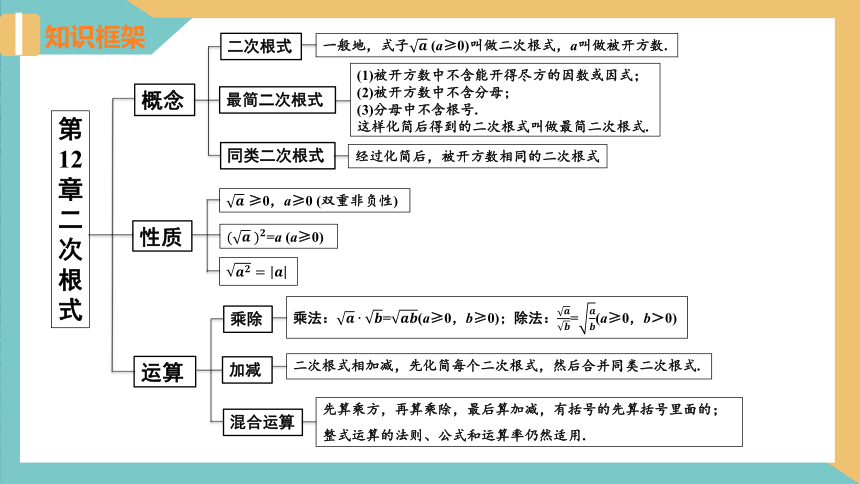
知识框架
第12章
二次根式
概念
性质
运算
二次根式
一般地,式子 (a≥0)叫做二次根式,a叫做被开方数.
最简二次根式
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含根号.
这样化简后得到的二次根式叫做最简二次根式.
同类二次根式
经过化简后,被开方数相同的二次根式
≥0,a≥0 (双重非负性)
=a (a≥0)
乘除
加减
混合运算
乘法:=(a≥0,b≥0);除法:=(a≥0,b>0)
二次根式相加减,先化简每个二次根式,然后合并同类二次根式.
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的;
整式运算的法则、公式和运算率仍然适用.
考点分析
考点一 二次根式的识别
①; ②; ③; ④(m≤0); ⑤(x、y异号);
⑥; ⑦; ⑧(a≥0).
例1 下列各式中,哪些是二次根式
解:①、④、⑥、⑦、⑧是二次根式.
(1)形式上:
含有二次根号“”,注意三次根号“”等都不可以;
方法总结
判断二次根式的方法:
(2)内容上:
被开方数必须是非负数,注意被开方数可以是数、字母或含有字母的式子.
巩固练习
2.a是任意实数,下列各式中:①;②;③;
④;⑤,一定是二次根式是_________(填序号).
②③④
1.下列式子是二次根式的是 ( )
A. B. C. D.
C
考点分析
考点二 二次根式有意义的条件
例2 要使下列各式有意义,x应是怎样的实数?
(1) ;
(2) ;
(2)不论x取何实数,总有x2≥0,x2+1≥1,二次根式在实数范
围内总有意义;
解:(1)要使有意义,必须x-5≥0,即x≥5;
(3) ;
(4) +
例2 要使下列各式有意义,x应是怎样的实数?
(3) 由题目条件,得:
解①得:x≤,
解②得:x≠,
∴不等式组的解集为:x<.
∴当x<时,式子 在实数范围内有意义.
考点分析
(1) ;
(2) ;
(3) ;
(4) +
例2 要使下列各式有意义,x应是怎样的实数?
(4) 由题目条件,得:
解①得:x≤,
解②得:x,
∴不等式组的解集为: 2≤x≤.
∴当2≤x≤时,式子+在实数范围内有意义.
考点分析
(1) ;
(2) ;
(3) ;
(4) +
考点分析
变式 已知y=++x+3,求的值.
解:∵y=++x+3,
∴x-3≥0,3-x≥0,
∴x=3,故y=6,
∴==3.
方法总结
确定使代数式有意义的字母的取值范围时,常常从以下三个方面来考虑:(1)被开方数大于或等于0;
(2)分母不能为0;
(3)零次幂或负整数指数幂的底数不能为0.
巩固练习
1.下列二次根式,无论x取什么值都有意义的是( )
A. B. C. D.
D
2.要使代数式有意义,则x的取值范围为____________.
x≥-2且x≠0
3.使代数式有意义的整数有_______________.
、、0、1
巩固练习
4. 已知,均为实数,,求的值.
解:∵,
∴
∴ ,
∴,
∴.
考点分析
例3 ,为实数,且,
化简:
解:∵式子要有意义,
∴
∴,,
∴
.
考点三 二次根式的性质
巩固练习
1. 若=2-b,则b满足的条件是( )
A.b>2 B.b<2 C.b≥2 D.b≤2
D
2.化简-()2的结果是( )
A.-2x-1 B.2x-1 C.1 D.-1
C
巩固练习
3.若=()2,则a应满足的条件是________.
a≥0
4.已知实数a,b满足+|6-b|=0,则的值为________.
5. 实数在数轴上的位置如图所示,化简: ______.
类比归纳
(a≥0)与的区别与联系
表 达 式 ()2=a(a≥0) =|a|
区 别 表示意义不同 表示a(a≥0)的算术平方根的平方 表示a的平方的算术平方根
取值范围不同 a为非负数,即a≥0 a取一切实数
运算顺序不同 先求非负实数a的算术平方根,然后再进行平方运算 先求实数a的平方,再求a2的算术平方根
运算结果不同 ()2=a(a≥0) =|a|=
联 系 ()2(a≥0)与的结果均为非负数,且当a≥0时,=()2
考点分析
考点四 最简二次根式的识别
(1) ;(2);(3);(4);(5);(6) .
解:(1)不是最简二次根式,被开方数含能开得尽方的因式;
(2)不是最简二次根式,被开方数含分母.
(3)是最简二次根式,被开方数不含分母;被开方数不含能开得尽方的因数或因式;
(4)是最简二次根式,被开方数不含分母;被开方数不含能开得尽方的因数或因式;
(5)不是最简二次根式,被开方数含分母.
(6) 不是最简二次根式,被开方数含分母.
例4 判断下列各式中哪些是最简二次根式,哪些不是?为什么?
方法总结
判断是否是最简二次根式,满足以下三个条件:
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
巩固练习
D
2.若是最简二次根式,则m、n的值为_______________.
3.若二次根式是最简二次根式,则正整数a的最小值是___.
m=0,n=-1
2
巩固练习
4. 若与是被开方数相同的最简二次根式,求的值.
解:∵ 与是被开方数相同的最简二次根式,
解得: ,
且符合题意,
.
考点分析
考点五 同类二次根式
例5 已知为最简二次根式,且与为同类二次根式,求的值,并求出这两个二次根式的积.
解:,
∵与为同类二次根式,
∴,
解得:,
这两个二次根式的积为.
2.若与最简二次根式是同类二次根式,则a=________.
1
巩固练习
1.下列各组二次根式中,化简后是同类二次根式的是( )
A.与 B.与 C.与 D.与
D
3.若两个最简二次根式与可以合并,则a=_____,b=_______.
1
1
考点分析
考点六 二次根式的运算
(1) (--3)×;
例6 计算:
解:(1)原式=(-2-)×2
=(-3)×2
=-18;
巩固练习
(2) (-1)2+×(+2)-(+1)(-1).
解:(2)原式=3-2++2-(-+-1)
=3-2+2-+-+1
=4+-.
例6 计算:
方法总结
(2)进行二次根式的混合运算时,整式运算的法则、公式和运算率仍然适用.
二次根式混合运算:
(1)确定运算顺序:先算乘方,再算乘除,最后算加减,同级运算按从左向右的顺序进行,有括号的先算括号内的.
巩固练习
1.如果=-x,那么x的取值范围是( )
A.x≤0 B.x≥-3 C.-3≤x≤0 D.x≤-3或x≥0
C
2.化简a的结果是( )
A. B. C.- D.-a
C
巩固练习
3.下列计算中,结果正确的是( )
A.×=3 B.+=2
C.÷= D.-=-
C
4.△ABC的两边长分别为2,5,则第三边的长度不可能为( )
A.3 B.4 C.5 D.6
A
巩固练习
5.比较大小:
① ;
② ;
③.
>
<
<
6.计算:
(1) ×-÷;
解:(1)原式=2-
=
=-;
(2)(+1)(-1)-(-1)2
(2)原式=4-6-(3-2+)
=-2-1-
=-.
巩固练习
巩固练习
7.已知:如图,中,,,,求:的面积;斜边的长.
B
A
C
解:中,,,
,
的面积;
中,,,
,
由勾股定理得:,
即的长是.
8.二次根式中有这样一些相铺相成的“对子”:,,它们的积不含根号,我们称这两个二次根式互为有理化因式.于是,二次根式的除法可以这样解:例如,,像这样通过分子、分母同乘一个式子把分母中的根号化去叫做分母有理化.分母有理化除了可以进行运算,还有其它一些用处.
解:(1)原式
=
=
;
(1)计算:;
巩固练习
(2)比较:与的大小;
,
,即,
;
(2)
=
=
,
巩固练习
(3)化简:.
(3)
=
=
=
.
巩固练习
考点分析
考点七 与二次根式有关的化简求值
例7 已知a=-2,b=+2,分别求下列代数式的值:
(1)a2b-ab2; (2)a2+ab+b2.
解:(1)∵a=-2,b=+2,
∴a2b-ab2=ab(a-b)
=(-2)(+2)(-2--2)
=[()2-22]×(-4)
=(-1)×(-4)
=4.
(2)∵a=-2,b=+2,
∴a2+ab+b2
=(a+b)2-ab
=(-2++2)2-(-2)(+2)
=(2)2-[()2-22]
=12+1
=13.
巩固练习
1. 化简()2022 ()2023的结果为( )
A.﹣﹣2 B.﹣2 C.+2 D.﹣1
C
2. 已知,则( )
A. B.6 C.4 D.12
C
巩固练习
3.已知x=,y=,求下列各式的值:
(2)x2-2xy+y2.
(1)x2-y2;
解:(1)当x=,y=时,
原式=(x+y)(x-y)
=()×()
=2×(1-)
=2-2.
(2)当x=,y=时,
原式=(x-y)2
=
=
=3-2.
巩固练习
4.已知a=,求式子的值.
解:∵a==2-,
∴a-1<0.
原式==
=2--1+
=3.
巩固练习
5. 已知:x是的整数部分,y是其小数部分,求的值.
解:∵,
∴,
由题意得,,
∴.
巩固练习
6.设一个三角形的三边长分别为a,b,c,p=(a+b+c),则有下列面积公式:
S=(海伦公式),S= (秦九韶公式).
(1)当a=7,b=8,c=9时,请你利用海伦公式求三角形的面积;
解:∵p= =12,
∴由海伦公式得
S== =12 .
巩固练习
(2)当a=,b=2,c=3时,请你利用秦九韶公式求三角形的面积.
解:由秦九韶公式得
S=
=
=
= .
课堂小结
谈谈你本节课的收获是什么?
第12章 二次根式
小结与思考
学习目标
1.整理、总结二次根式的相关知识,在巩固基本知识的基础上学会灵活运用;
2.感受化归的数学思想,提高探究问题的能力.
知识框架
第12章
二次根式
概念
性质
运算
二次根式
一般地,式子 (a≥0)叫做二次根式,a叫做被开方数.
最简二次根式
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含根号.
这样化简后得到的二次根式叫做最简二次根式.
同类二次根式
经过化简后,被开方数相同的二次根式
≥0,a≥0 (双重非负性)
=a (a≥0)
乘除
加减
混合运算
乘法:=(a≥0,b≥0);除法:=(a≥0,b>0)
二次根式相加减,先化简每个二次根式,然后合并同类二次根式.
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的;
整式运算的法则、公式和运算率仍然适用.
考点分析
考点一 二次根式的识别
①; ②; ③; ④(m≤0); ⑤(x、y异号);
⑥; ⑦; ⑧(a≥0).
例1 下列各式中,哪些是二次根式
解:①、④、⑥、⑦、⑧是二次根式.
(1)形式上:
含有二次根号“”,注意三次根号“”等都不可以;
方法总结
判断二次根式的方法:
(2)内容上:
被开方数必须是非负数,注意被开方数可以是数、字母或含有字母的式子.
巩固练习
2.a是任意实数,下列各式中:①;②;③;
④;⑤,一定是二次根式是_________(填序号).
②③④
1.下列式子是二次根式的是 ( )
A. B. C. D.
C
考点分析
考点二 二次根式有意义的条件
例2 要使下列各式有意义,x应是怎样的实数?
(1) ;
(2) ;
(2)不论x取何实数,总有x2≥0,x2+1≥1,二次根式在实数范
围内总有意义;
解:(1)要使有意义,必须x-5≥0,即x≥5;
(3) ;
(4) +
例2 要使下列各式有意义,x应是怎样的实数?
(3) 由题目条件,得:
解①得:x≤,
解②得:x≠,
∴不等式组的解集为:x<.
∴当x<时,式子 在实数范围内有意义.
考点分析
(1) ;
(2) ;
(3) ;
(4) +
例2 要使下列各式有意义,x应是怎样的实数?
(4) 由题目条件,得:
解①得:x≤,
解②得:x,
∴不等式组的解集为: 2≤x≤.
∴当2≤x≤时,式子+在实数范围内有意义.
考点分析
(1) ;
(2) ;
(3) ;
(4) +
考点分析
变式 已知y=++x+3,求的值.
解:∵y=++x+3,
∴x-3≥0,3-x≥0,
∴x=3,故y=6,
∴==3.
方法总结
确定使代数式有意义的字母的取值范围时,常常从以下三个方面来考虑:(1)被开方数大于或等于0;
(2)分母不能为0;
(3)零次幂或负整数指数幂的底数不能为0.
巩固练习
1.下列二次根式,无论x取什么值都有意义的是( )
A. B. C. D.
D
2.要使代数式有意义,则x的取值范围为____________.
x≥-2且x≠0
3.使代数式有意义的整数有_______________.
、、0、1
巩固练习
4. 已知,均为实数,,求的值.
解:∵,
∴
∴ ,
∴,
∴.
考点分析
例3 ,为实数,且,
化简:
解:∵式子要有意义,
∴
∴,,
∴
.
考点三 二次根式的性质
巩固练习
1. 若=2-b,则b满足的条件是( )
A.b>2 B.b<2 C.b≥2 D.b≤2
D
2.化简-()2的结果是( )
A.-2x-1 B.2x-1 C.1 D.-1
C
巩固练习
3.若=()2,则a应满足的条件是________.
a≥0
4.已知实数a,b满足+|6-b|=0,则的值为________.
5. 实数在数轴上的位置如图所示,化简: ______.
类比归纳
(a≥0)与的区别与联系
表 达 式 ()2=a(a≥0) =|a|
区 别 表示意义不同 表示a(a≥0)的算术平方根的平方 表示a的平方的算术平方根
取值范围不同 a为非负数,即a≥0 a取一切实数
运算顺序不同 先求非负实数a的算术平方根,然后再进行平方运算 先求实数a的平方,再求a2的算术平方根
运算结果不同 ()2=a(a≥0) =|a|=
联 系 ()2(a≥0)与的结果均为非负数,且当a≥0时,=()2
考点分析
考点四 最简二次根式的识别
(1) ;(2);(3);(4);(5);(6) .
解:(1)不是最简二次根式,被开方数含能开得尽方的因式;
(2)不是最简二次根式,被开方数含分母.
(3)是最简二次根式,被开方数不含分母;被开方数不含能开得尽方的因数或因式;
(4)是最简二次根式,被开方数不含分母;被开方数不含能开得尽方的因数或因式;
(5)不是最简二次根式,被开方数含分母.
(6) 不是最简二次根式,被开方数含分母.
例4 判断下列各式中哪些是最简二次根式,哪些不是?为什么?
方法总结
判断是否是最简二次根式,满足以下三个条件:
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数中不含分母;
(3)分母中不含有根号.
1.下列二次根式中属于最简二次根式的是( )
A. B. C. D.
巩固练习
D
2.若是最简二次根式,则m、n的值为_______________.
3.若二次根式是最简二次根式,则正整数a的最小值是___.
m=0,n=-1
2
巩固练习
4. 若与是被开方数相同的最简二次根式,求的值.
解:∵ 与是被开方数相同的最简二次根式,
解得: ,
且符合题意,
.
考点分析
考点五 同类二次根式
例5 已知为最简二次根式,且与为同类二次根式,求的值,并求出这两个二次根式的积.
解:,
∵与为同类二次根式,
∴,
解得:,
这两个二次根式的积为.
2.若与最简二次根式是同类二次根式,则a=________.
1
巩固练习
1.下列各组二次根式中,化简后是同类二次根式的是( )
A.与 B.与 C.与 D.与
D
3.若两个最简二次根式与可以合并,则a=_____,b=_______.
1
1
考点分析
考点六 二次根式的运算
(1) (--3)×;
例6 计算:
解:(1)原式=(-2-)×2
=(-3)×2
=-18;
巩固练习
(2) (-1)2+×(+2)-(+1)(-1).
解:(2)原式=3-2++2-(-+-1)
=3-2+2-+-+1
=4+-.
例6 计算:
方法总结
(2)进行二次根式的混合运算时,整式运算的法则、公式和运算率仍然适用.
二次根式混合运算:
(1)确定运算顺序:先算乘方,再算乘除,最后算加减,同级运算按从左向右的顺序进行,有括号的先算括号内的.
巩固练习
1.如果=-x,那么x的取值范围是( )
A.x≤0 B.x≥-3 C.-3≤x≤0 D.x≤-3或x≥0
C
2.化简a的结果是( )
A. B. C.- D.-a
C
巩固练习
3.下列计算中,结果正确的是( )
A.×=3 B.+=2
C.÷= D.-=-
C
4.△ABC的两边长分别为2,5,则第三边的长度不可能为( )
A.3 B.4 C.5 D.6
A
巩固练习
5.比较大小:
① ;
② ;
③.
>
<
<
6.计算:
(1) ×-÷;
解:(1)原式=2-
=
=-;
(2)(+1)(-1)-(-1)2
(2)原式=4-6-(3-2+)
=-2-1-
=-.
巩固练习
巩固练习
7.已知:如图,中,,,,求:的面积;斜边的长.
B
A
C
解:中,,,
,
的面积;
中,,,
,
由勾股定理得:,
即的长是.
8.二次根式中有这样一些相铺相成的“对子”:,,它们的积不含根号,我们称这两个二次根式互为有理化因式.于是,二次根式的除法可以这样解:例如,,像这样通过分子、分母同乘一个式子把分母中的根号化去叫做分母有理化.分母有理化除了可以进行运算,还有其它一些用处.
解:(1)原式
=
=
;
(1)计算:;
巩固练习
(2)比较:与的大小;
,
,即,
;
(2)
=
=
,
巩固练习
(3)化简:.
(3)
=
=
=
.
巩固练习
考点分析
考点七 与二次根式有关的化简求值
例7 已知a=-2,b=+2,分别求下列代数式的值:
(1)a2b-ab2; (2)a2+ab+b2.
解:(1)∵a=-2,b=+2,
∴a2b-ab2=ab(a-b)
=(-2)(+2)(-2--2)
=[()2-22]×(-4)
=(-1)×(-4)
=4.
(2)∵a=-2,b=+2,
∴a2+ab+b2
=(a+b)2-ab
=(-2++2)2-(-2)(+2)
=(2)2-[()2-22]
=12+1
=13.
巩固练习
1. 化简()2022 ()2023的结果为( )
A.﹣﹣2 B.﹣2 C.+2 D.﹣1
C
2. 已知,则( )
A. B.6 C.4 D.12
C
巩固练习
3.已知x=,y=,求下列各式的值:
(2)x2-2xy+y2.
(1)x2-y2;
解:(1)当x=,y=时,
原式=(x+y)(x-y)
=()×()
=2×(1-)
=2-2.
(2)当x=,y=时,
原式=(x-y)2
=
=
=3-2.
巩固练习
4.已知a=,求式子的值.
解:∵a==2-,
∴a-1<0.
原式==
=2--1+
=3.
巩固练习
5. 已知:x是的整数部分,y是其小数部分,求的值.
解:∵,
∴,
由题意得,,
∴.
巩固练习
6.设一个三角形的三边长分别为a,b,c,p=(a+b+c),则有下列面积公式:
S=(海伦公式),S= (秦九韶公式).
(1)当a=7,b=8,c=9时,请你利用海伦公式求三角形的面积;
解:∵p= =12,
∴由海伦公式得
S== =12 .
巩固练习
(2)当a=,b=2,c=3时,请你利用秦九韶公式求三角形的面积.
解:由秦九韶公式得
S=
=
=
= .
课堂小结
谈谈你本节课的收获是什么?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
