数学:5.5一元一次不等式组及其解法同步练习1(北京课改版七年级下)
文档属性
| 名称 | 数学:5.5一元一次不等式组及其解法同步练习1(北京课改版七年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 53.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 09:27:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
5.5 一元一次不等式组及其解法 同步练习
【主干知识】
认真预习教材,尝试完成下列各题:
1.我们把两个(或两个以上)的______,就组成了一个一元一次不等式组.
2.不等式组的几个一元一次不等式的_________,叫做由它们所组成的一元一次不等式组的解集.
3.求不等式组的__________的过程叫做解不等式组.
4.借助数轴,求出下列不等式组的解集,然后看能总结出什么规律:
(1)
5.解一元一次不等式组,可分以下两个步骤:
(1)求出该不等式组中_________;
(2)利用数轴求出________,就求出了这个不等式组的解集.
6.自编一个解集为x≥2的一元一次不等式组____________.
7.一元一次不等式组的解集是( )
A.-2【点击思维】
1.你认为怎样找两个不等式解集的公共部分?
2.一个一元一次不等式组一定有解吗?并举例说明.
3.若不等式组的解集是空集,则a、b的大小关系是______.
4.解集为-2A.
【典例分析】
例1 解不等式组并把这个不等式组的解集在数轴上表示出来.
思路分析:本题应选求出不等式组各个不等式的解集,然后再求出这两个解集的公共部分(可借助于数轴).
解:原不等式组变形为
解不等式①得x≥-1
解不等式②得x<9
所以这个不等式组的解集为-1≤x<9.
它的解集在数轴上的表示如图所示:
方法点拨:解一元一次不等式组,在求出不等式组中各个不等式的解集后,一般都要利用数轴求出这些不等式的解集的公共部分(当各个不等式的解集没有公共部分时,表示这个不等式组无解).这种数形结合的思想方法既直观、又迅速、准确,一定要熟练掌握.待熟练之后,也可不画数轴,借助如下的口诀:“大大取较大,小小取较小,大小小大中间找,大大小小解不了”也可迎刃而解,此时数轴及不等式解集的形象会在脑中油然而生,但如果要求画数轴时,必须画出来.
例2 用若干辆载重为8吨的汽车运一批货物,若每辆汽车只装5吨,则剩下10吨货物.若每辆汽车装满8吨,则最后一辆汽车不空也不满,请问有多少辆汽车?
思路分析:解决本题的关键在于正确理解“不空也不满”的意思.最后一辆汽车不空也不满的意思是这辆汽车装的货物大于0吨而小于8吨.
解:设有x辆汽车,则有货物(5x+10)吨,(x-1)辆汽车装满货物共装8(x-1)吨,根据最后一辆汽车不空也不满,可列得不等式组.
解不等式①得x<6
解不等式②得x>
所以不等式组的解集为答:有4辆或5辆汽车.
方法点拨:不等式(组)的应用题取材广泛,背景鲜活,内容丰富,贴近现实生活,近年来越来越受到人们的普遍关注,也成为中考的热点问题.解题关键在于理清题意,抓住题目中的关键词语,比如“最多”“最少”“不大于”“不小于”“超过”“至少”“至多”等,寻找不等关系,建立不等式(或组)予以解决.
【基础能力训练】
1.判断下列式子中,哪些是一元一次不等式组?
(1)
2.下列说法不正确的是( )
A.不等式组的解集为x≥2; B.2是不等式组的一个解
C.不等式组的解集是1≤x≤-; D.不等式组无解
3.不等式组的解集是________,不等式组的解集是_______.
4.不等式组的解集是______,不等式组的解集是________.
5.解集是如图所示的不等式组为( )
A.
6.用数轴表示下列各组不等式组的解集:
(1)
7.不等式组的解集是_______,这个不等式组的整数解为________.
8.已知不等式①②③的解集在数轴上的表示如图所示,则它们的公共部分的解集是( )
A.-1≤x<3 B.1≤x<3 C.-1≤x<1 D.无解
9.解下列不等式组:
(1)
10.解下列不等式组:
(1)
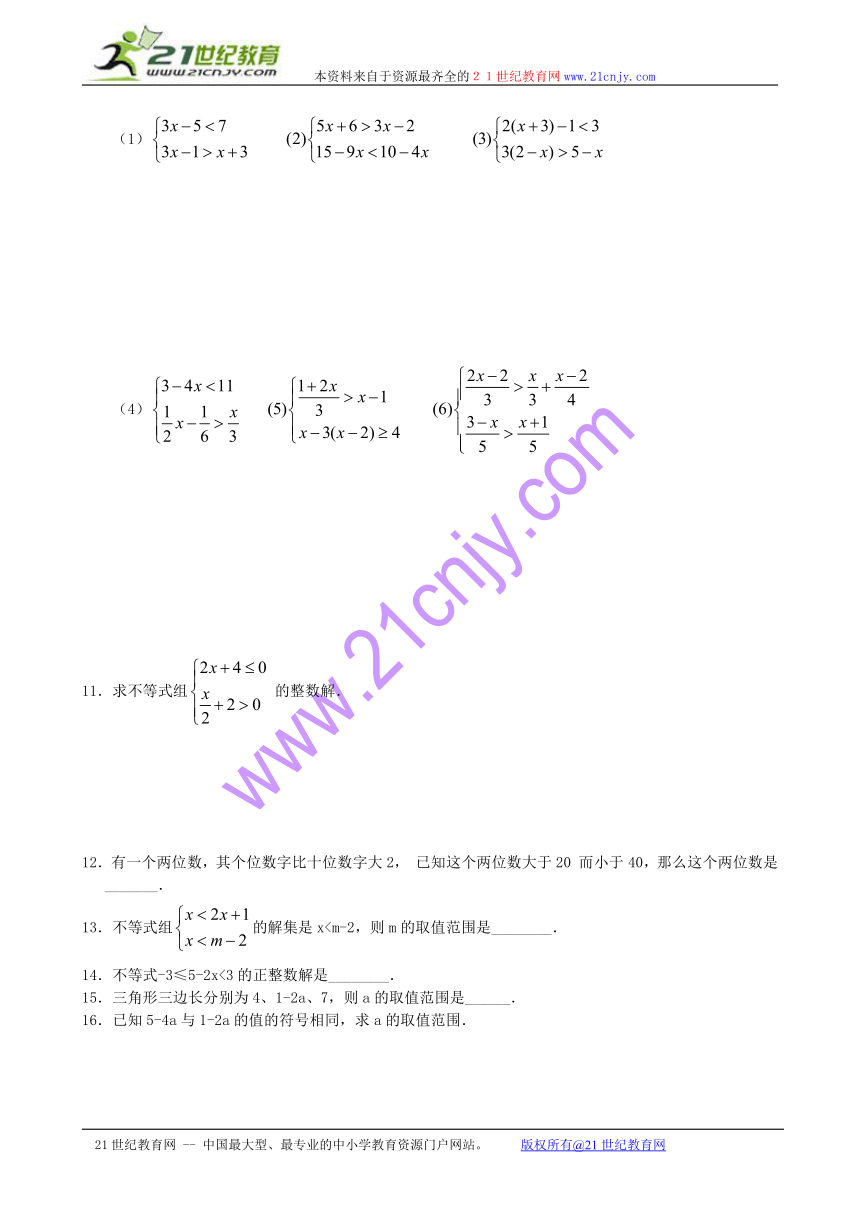
(4)
11.求不等式组的整数解.
12.有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20而小于40,那么这个两位数是_______.
13.不等式组的解集是x14.不等式-3≤5-2x<3的正整数解是________.
15.三角形三边长分别为4、1-2a、7,则a的取值范围是______.
16.已知5-4a与1-2a的值的符号相同,求a的取值范围.
17.已知关于x的方程5x-2m=3x-6m+1的解满足-318.若关于x的不等式组的解集为-119.把一篮苹果分给若干个小朋友,每人分5个,则还余2个;每人分6个,那么最后一个小朋友分得的苹果少于2个,求小朋友的人数和苹果的个数.
20.某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取煤用煤总量不足68吨,该校计划每日烧煤多少吨?
【综合创新训练】
21.已知不等式组
(1)若此不等式组无解,求a的取值范围,并利用数轴说明.
(2)若此不等式组有解,求a的取值范围,并利用数轴说明.
22.已知不等式组的解集为-123.某城市的出租汽车起步价是10元(即行驶路程在5千米以内都需付10元车费),达到5千米后,每增加1千米加价1.2元(不足1千米的部分按1千米计算),现在某人乘这种出租车由甲地到乙地共付车费17.2元,从甲地到乙地的路程大致是多少?
24.某服装厂现有甲种布料42米,乙种布料30米,现计划用这两种布料做M、N两种型号的校服共40件,已知做一件M型号的校服需要用甲种布料0.8米,乙种布料1.1米,做一件N型号的校服需用甲种布料1.2米,乙种布料0.5米,按要求生产M、N两种型号的校服,有哪几种生产方案?请你设计出来.
【探究学习】
世界上第一个应用数学家──阿基米德
人们称阿基米德为“数学之神”,主要赞叹他能把枯燥而抽象的数学,千变万化地应用于实际.
阿基米德把他的知识完全献给了自己的祖国.在一次罗马军队攻占他所居住的叙拉古城时,他发明了威力无比的抗敌器械:一种庞大的超重机械,这机械能抓住敌人的船只,将其摔出老远;他发明的一种武器,可以投射大石堆,若干块大石堆犹如暴风雨般射向敌群,使罗马士兵胆战心惊;他还利用圆锥曲线的知识,设计了一种火镜,转动火镜反射后太阳能使船焚烧;他设计了一种投火器,可以把燃烧的东西弹出去焚烧敌船的士兵.阿基米德的名字使罗马士兵闻风丧胆,而自己为同胞所敬仰.
答案:
【主干知识】
1.一元一次不等式合在一起 2.解集的公共部分 3.解集
4.(1)x>3 (2)x<1 (3)1规律:大大取较大,小小取较小,大小小大中间我,大大小小无处找.
5.(1)各个不等式的解集
(2)这些不等式解集的公共部分
6. 7.C
【点击思维】
1.在同一条数轴上画出这两个不等式的解集后,看两条线重合部分在数轴上是哪些数,这些数用一个不等式描述出来即可.
2.不一定,比如,从数轴上看:
画出的两条线没有公共部分;从不等式组的解集的定义上看,根本找不到既大于3又小于-1的数.
3.a≤b 解析:是空集说明x大于一个大数同时又小于一个较小的数,
也可能这两数相等,所以应是a≤b.
4.D 解析:解2x-1<5得x<3,解不等式-5x<2x+14,得x>-2,
所以该不等式组的解集是-2【基础能力训练】
1.(3)(5)是.
2.C 3.26.(1) (2)
(3) (4)
7.-19.(1)-37
10.(1)21 (3)x<-1 (4)x>1 (5)x≤1 (6)无解
11.-3,-2 12.24或35 13.m≥-3
14.2,3,4 15.-5
17.-≤m< 18.15
19.小朋友有7个,苹果有37个;或小朋友有8个,苹果有42个.
20.设计划每日烧煤x吨,由题意得 解这个不等式组,得20所以该校计划每日烧煤大于20吨而又小于22吨.
【综合创新训练】
21.(1)若不等式组无解,说明属于“大大小小无处找”或-3=a的情形,因此a≤-3.
(2)若有解,则与(1)的情形相反,a应取≤-3以外的数即a>-3.
22.由不等式①得x<,由不等式②得x>2b+3,又因为不等式组的解集是-1所以
所以(a+2)(b+2)=(1+1)(-2+2)=0.
23.设从甲地到乙地的路程大约是x千米,根据题意,得16<10+1.2(x-5)≤17.2解此不等式组,得1024.设生产M型的校服x件,则N型生产(40-x)件,根据题意,得 解这个不等式组,得15≤x≤16,又因x取整数,所以x=15或16.当x=15时,40-x=25;当x=16时,40-x=24,所以共有两种生产方案:
方案一:生产M型号的校服15件,N型号的校服25件;
方案二:生产M型号的校服16件,N型号的校服24件.
①②
①②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
5.5 一元一次不等式组及其解法 同步练习
【主干知识】
认真预习教材,尝试完成下列各题:
1.我们把两个(或两个以上)的______,就组成了一个一元一次不等式组.
2.不等式组的几个一元一次不等式的_________,叫做由它们所组成的一元一次不等式组的解集.
3.求不等式组的__________的过程叫做解不等式组.
4.借助数轴,求出下列不等式组的解集,然后看能总结出什么规律:
(1)
5.解一元一次不等式组,可分以下两个步骤:
(1)求出该不等式组中_________;
(2)利用数轴求出________,就求出了这个不等式组的解集.
6.自编一个解集为x≥2的一元一次不等式组____________.
7.一元一次不等式组的解集是( )
A.-2
1.你认为怎样找两个不等式解集的公共部分?
2.一个一元一次不等式组一定有解吗?并举例说明.
3.若不等式组的解集是空集,则a、b的大小关系是______.
4.解集为-2
【典例分析】
例1 解不等式组并把这个不等式组的解集在数轴上表示出来.
思路分析:本题应选求出不等式组各个不等式的解集,然后再求出这两个解集的公共部分(可借助于数轴).
解:原不等式组变形为
解不等式①得x≥-1
解不等式②得x<9
所以这个不等式组的解集为-1≤x<9.
它的解集在数轴上的表示如图所示:
方法点拨:解一元一次不等式组,在求出不等式组中各个不等式的解集后,一般都要利用数轴求出这些不等式的解集的公共部分(当各个不等式的解集没有公共部分时,表示这个不等式组无解).这种数形结合的思想方法既直观、又迅速、准确,一定要熟练掌握.待熟练之后,也可不画数轴,借助如下的口诀:“大大取较大,小小取较小,大小小大中间找,大大小小解不了”也可迎刃而解,此时数轴及不等式解集的形象会在脑中油然而生,但如果要求画数轴时,必须画出来.
例2 用若干辆载重为8吨的汽车运一批货物,若每辆汽车只装5吨,则剩下10吨货物.若每辆汽车装满8吨,则最后一辆汽车不空也不满,请问有多少辆汽车?
思路分析:解决本题的关键在于正确理解“不空也不满”的意思.最后一辆汽车不空也不满的意思是这辆汽车装的货物大于0吨而小于8吨.
解:设有x辆汽车,则有货物(5x+10)吨,(x-1)辆汽车装满货物共装8(x-1)吨,根据最后一辆汽车不空也不满,可列得不等式组.
解不等式①得x<6
解不等式②得x>
所以不等式组的解集为
方法点拨:不等式(组)的应用题取材广泛,背景鲜活,内容丰富,贴近现实生活,近年来越来越受到人们的普遍关注,也成为中考的热点问题.解题关键在于理清题意,抓住题目中的关键词语,比如“最多”“最少”“不大于”“不小于”“超过”“至少”“至多”等,寻找不等关系,建立不等式(或组)予以解决.
【基础能力训练】
1.判断下列式子中,哪些是一元一次不等式组?
(1)
2.下列说法不正确的是( )
A.不等式组的解集为x≥2; B.2是不等式组的一个解
C.不等式组的解集是1≤x≤-; D.不等式组无解
3.不等式组的解集是________,不等式组的解集是_______.
4.不等式组的解集是______,不等式组的解集是________.
5.解集是如图所示的不等式组为( )
A.
6.用数轴表示下列各组不等式组的解集:
(1)
7.不等式组的解集是_______,这个不等式组的整数解为________.
8.已知不等式①②③的解集在数轴上的表示如图所示,则它们的公共部分的解集是( )
A.-1≤x<3 B.1≤x<3 C.-1≤x<1 D.无解
9.解下列不等式组:
(1)
10.解下列不等式组:
(1)
(4)
11.求不等式组的整数解.
12.有一个两位数,其个位数字比十位数字大2,已知这个两位数大于20而小于40,那么这个两位数是_______.
13.不等式组的解集是x
15.三角形三边长分别为4、1-2a、7,则a的取值范围是______.
16.已知5-4a与1-2a的值的符号相同,求a的取值范围.
17.已知关于x的方程5x-2m=3x-6m+1的解满足-3
20.某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨煤,那么取煤用煤总量不足68吨,该校计划每日烧煤多少吨?
【综合创新训练】
21.已知不等式组
(1)若此不等式组无解,求a的取值范围,并利用数轴说明.
(2)若此不等式组有解,求a的取值范围,并利用数轴说明.
22.已知不等式组的解集为-1
24.某服装厂现有甲种布料42米,乙种布料30米,现计划用这两种布料做M、N两种型号的校服共40件,已知做一件M型号的校服需要用甲种布料0.8米,乙种布料1.1米,做一件N型号的校服需用甲种布料1.2米,乙种布料0.5米,按要求生产M、N两种型号的校服,有哪几种生产方案?请你设计出来.
【探究学习】
世界上第一个应用数学家──阿基米德
人们称阿基米德为“数学之神”,主要赞叹他能把枯燥而抽象的数学,千变万化地应用于实际.
阿基米德把他的知识完全献给了自己的祖国.在一次罗马军队攻占他所居住的叙拉古城时,他发明了威力无比的抗敌器械:一种庞大的超重机械,这机械能抓住敌人的船只,将其摔出老远;他发明的一种武器,可以投射大石堆,若干块大石堆犹如暴风雨般射向敌群,使罗马士兵胆战心惊;他还利用圆锥曲线的知识,设计了一种火镜,转动火镜反射后太阳能使船焚烧;他设计了一种投火器,可以把燃烧的东西弹出去焚烧敌船的士兵.阿基米德的名字使罗马士兵闻风丧胆,而自己为同胞所敬仰.
答案:
【主干知识】
1.一元一次不等式合在一起 2.解集的公共部分 3.解集
4.(1)x>3 (2)x<1 (3)1
5.(1)各个不等式的解集
(2)这些不等式解集的公共部分
6. 7.C
【点击思维】
1.在同一条数轴上画出这两个不等式的解集后,看两条线重合部分在数轴上是哪些数,这些数用一个不等式描述出来即可.
2.不一定,比如,从数轴上看:
画出的两条线没有公共部分;从不等式组的解集的定义上看,根本找不到既大于3又小于-1的数.
3.a≤b 解析:是空集说明x大于一个大数同时又小于一个较小的数,
也可能这两数相等,所以应是a≤b.
4.D 解析:解2x-1<5得x<3,解不等式-5x<2x+14,得x>-2,
所以该不等式组的解集是-2
1.(3)(5)是.
2.C 3.2
(3) (4)
7.-1
10.(1)2
11.-3,-2 12.24或35 13.m≥-3
14.2,3,4 15.-5
17.-≤m< 18.15
19.小朋友有7个,苹果有37个;或小朋友有8个,苹果有42个.
20.设计划每日烧煤x吨,由题意得 解这个不等式组,得20
【综合创新训练】
21.(1)若不等式组无解,说明属于“大大小小无处找”或-3=a的情形,因此a≤-3.
(2)若有解,则与(1)的情形相反,a应取≤-3以外的数即a>-3.
22.由不等式①得x<,由不等式②得x>2b+3,又因为不等式组的解集是-1
所以(a+2)(b+2)=(1+1)(-2+2)=0.
23.设从甲地到乙地的路程大约是x千米,根据题意,得16<10+1.2(x-5)≤17.2解此不等式组,得10
方案一:生产M型号的校服15件,N型号的校服25件;
方案二:生产M型号的校服16件,N型号的校服24件.
①②
①②
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
