数学:1.5测量物体的高度同步练习1(北师大版九年级下)
文档属性
| 名称 | 数学:1.5测量物体的高度同步练习1(北师大版九年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 38.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
1.5 测量物体的高度 同步练习
1. (16分)下表是小明同学填写活动报告的部分内容:
课题 在两岸近似平行的河段上测量河宽
测量目标图示
测得数据 ∠CAD=60°,AB=30m,∠CBD=45°,∠BDC=90°
请你根据以上的条件,计算出河宽CD(结果保留根号).
2. (16分)下面是活动报告的一部分, 请填写“测得数据”和“计算”两栏中未完成的部分.
课题 测量旗杆高
测量示意图
测得数据 测量项目 第一次 第二次 平均值
BD的长 24.19m 23.97m
测倾器的高 CD=1.23m CD=1.19m
倾斜角 a=31°15′ a=30°45′ a=31°
计算 旗杆高AB(精确到0.1m)
3. (17分)学习完本节内容后, 某校九年级数学老师布置一道利用测倾器测量学校旗杆高度的活动课题,下表是小明同学填写的活动报告,请你根据有关测量数据, 求旗杆高AB(计算过程填在下表计算栏内,用计算器计算).
活动报告
课题 利用测倾器测量学校旗杆的高
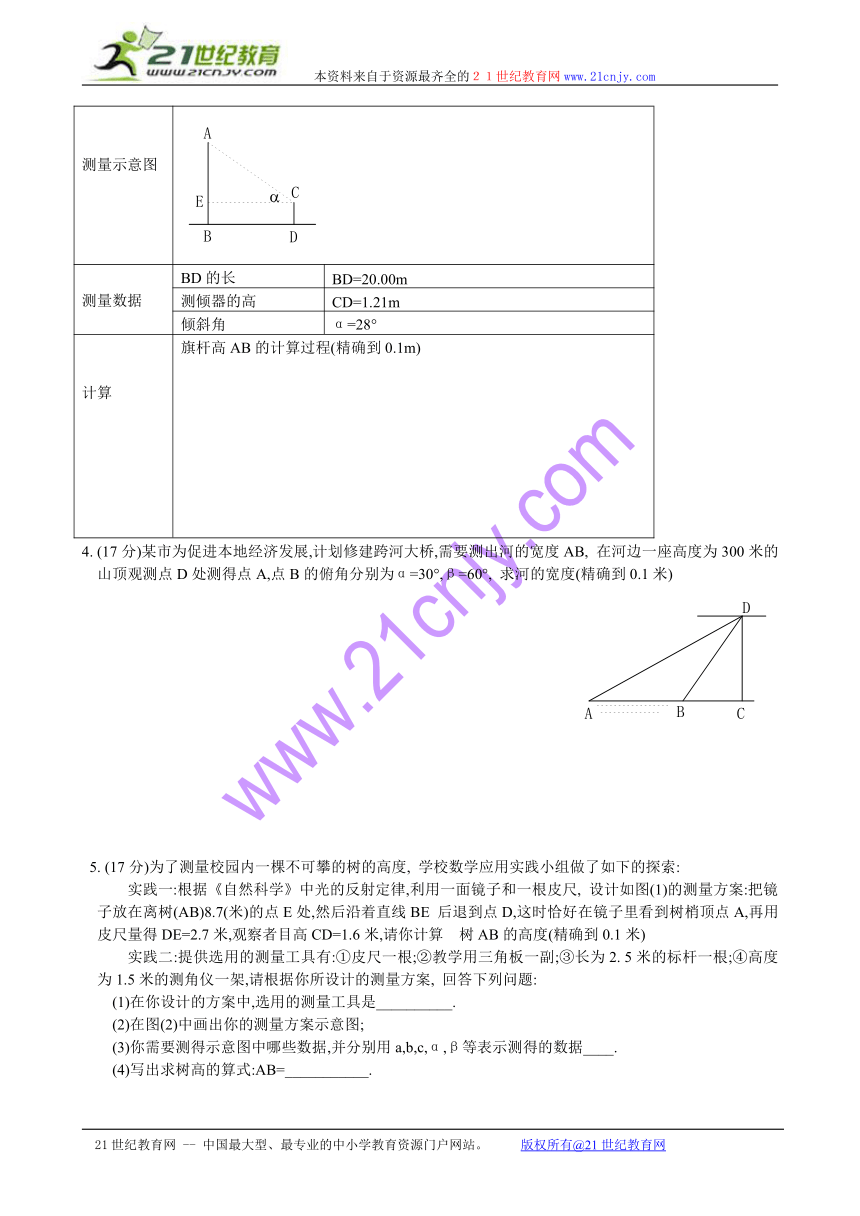
测量示意图
测量数据 BD的长 BD=20.00m
测倾器的高 CD=1.21m
倾斜角 α=28°
计算 旗杆高AB的计算过程(精确到0.1m)
4. (17分)某市为促进本地经济发展,计划修建跨河大桥,需要测出河的宽度AB, 在河边一座高度为300米的山顶观测点D处测得点A,点B的俯角分别为α=30°,β=60°, 求河的宽度(精确到0.1米)
5. (17分)为了测量校园内一棵不可攀的树的高度, 学校数学应用实践小组做了如下的探索:
实践一:根据《自然科学》中光的反射定律,利用一面镜子和一根皮尺, 设计如图(1)的测量方案:把镜子放在离树(AB)8.7(米)的点E处,然后沿着直线BE 后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算 树AB的高度(精确到0.1米)
实践二:提供选用的测量工具有:①皮尺一根;②教学用三角板一副;③长为2. 5米的标杆一根;④高度为1.5米的测角仪一架,请根据你所设计的测量方案, 回答下列问题:
(1)在你设计的方案中,选用的测量工具是__________.
(2)在图(2)中画出你的测量方案示意图;
(3)你需要测得示意图中哪些数据,并分别用a,b,c,α,β等表示测得的数据____.
(4)写出求树高的算式:AB=___________.
6. (17分)在1:50000的地图上,查得A点在300m的等高线上,B点在400m的等高线上, 在地图上量得AB的长为2.5cm,若要在A、B之间建一条索道,那么缆索至少要多长 它的倾斜角是多少
(说明:地图上量得的AB的长,就是A,B两点间的水平距离AB′,由B向过A 且平行于地面的平面作垂线,垂足为B′,连接AB′,则∠A即是缆索的倾斜角.)
答案:
1. 设AD=x(m),则在Rt△ACD中,∠CAD=60°,∠ADC=90°,
∴CD=AD·tan∠CAD=x ( m).
在Rt△BCD中,∠CBD=45°,∠BDC=90°,
∴CD=BD.又BD=AB+AD=20+x(m),
故20+x=x,
x=10(+1),
∴CD=x=30+10(m).
2.平均值:BD==24.08(m);
测倾器的高= =1.21(m).
∵AB=AE+BE,AE=CE·tanα, BE=CD,CE=BD.
∴AB=BD·tanα+CD=24.08×tan31°+1.21≈15.7(m).
3.在Rt△ACE中,AE=CE·tana,
∵BD=CE,∴AE=BD·tana=20.00×0.5317=10.634( m).
∵CD=BE,∴BE=1.21(m).
∴AB=AE+BE=10.634+1.21=11.844≈11.8(m).
4.在Rt△ACD中,∠ACD=90°,∠CDA=90°-30°=60°.
∴AC=CD·tan60°=CD=300 (米) .
在Rt△BCD中,∠BDC=90°-60°=30°,∴BC=DC·tan30°=DC=100 (米).
故AB=200≈346. 4(米).
5.实践一:∵∠CED=∠AEB,∠CDE=∠ABE=90°.
∴△CED∽△AEB.∴ ,即,∴AB= 5.2米.
实践二:如(1)①②;(2)示意图如图;(3)CD=a,BD=b;(4)AB=a+b.(说明:本题答案不惟一).
6.AB′=12500cm=1250m,从而AB=≈1254(m).
又tanA==0.08,故∠A≈4°34′.
300
350
400
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
1.5 测量物体的高度 同步练习
1. (16分)下表是小明同学填写活动报告的部分内容:
课题 在两岸近似平行的河段上测量河宽
测量目标图示
测得数据 ∠CAD=60°,AB=30m,∠CBD=45°,∠BDC=90°
请你根据以上的条件,计算出河宽CD(结果保留根号).
2. (16分)下面是活动报告的一部分, 请填写“测得数据”和“计算”两栏中未完成的部分.
课题 测量旗杆高
测量示意图
测得数据 测量项目 第一次 第二次 平均值
BD的长 24.19m 23.97m
测倾器的高 CD=1.23m CD=1.19m
倾斜角 a=31°15′ a=30°45′ a=31°
计算 旗杆高AB(精确到0.1m)
3. (17分)学习完本节内容后, 某校九年级数学老师布置一道利用测倾器测量学校旗杆高度的活动课题,下表是小明同学填写的活动报告,请你根据有关测量数据, 求旗杆高AB(计算过程填在下表计算栏内,用计算器计算).
活动报告
课题 利用测倾器测量学校旗杆的高
测量示意图
测量数据 BD的长 BD=20.00m
测倾器的高 CD=1.21m
倾斜角 α=28°
计算 旗杆高AB的计算过程(精确到0.1m)
4. (17分)某市为促进本地经济发展,计划修建跨河大桥,需要测出河的宽度AB, 在河边一座高度为300米的山顶观测点D处测得点A,点B的俯角分别为α=30°,β=60°, 求河的宽度(精确到0.1米)
5. (17分)为了测量校园内一棵不可攀的树的高度, 学校数学应用实践小组做了如下的探索:
实践一:根据《自然科学》中光的反射定律,利用一面镜子和一根皮尺, 设计如图(1)的测量方案:把镜子放在离树(AB)8.7(米)的点E处,然后沿着直线BE 后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算 树AB的高度(精确到0.1米)
实践二:提供选用的测量工具有:①皮尺一根;②教学用三角板一副;③长为2. 5米的标杆一根;④高度为1.5米的测角仪一架,请根据你所设计的测量方案, 回答下列问题:
(1)在你设计的方案中,选用的测量工具是__________.
(2)在图(2)中画出你的测量方案示意图;
(3)你需要测得示意图中哪些数据,并分别用a,b,c,α,β等表示测得的数据____.
(4)写出求树高的算式:AB=___________.
6. (17分)在1:50000的地图上,查得A点在300m的等高线上,B点在400m的等高线上, 在地图上量得AB的长为2.5cm,若要在A、B之间建一条索道,那么缆索至少要多长 它的倾斜角是多少
(说明:地图上量得的AB的长,就是A,B两点间的水平距离AB′,由B向过A 且平行于地面的平面作垂线,垂足为B′,连接AB′,则∠A即是缆索的倾斜角.)
答案:
1. 设AD=x(m),则在Rt△ACD中,∠CAD=60°,∠ADC=90°,
∴CD=AD·tan∠CAD=x ( m).
在Rt△BCD中,∠CBD=45°,∠BDC=90°,
∴CD=BD.又BD=AB+AD=20+x(m),
故20+x=x,
x=10(+1),
∴CD=x=30+10(m).
2.平均值:BD==24.08(m);
测倾器的高= =1.21(m).
∵AB=AE+BE,AE=CE·tanα, BE=CD,CE=BD.
∴AB=BD·tanα+CD=24.08×tan31°+1.21≈15.7(m).
3.在Rt△ACE中,AE=CE·tana,
∵BD=CE,∴AE=BD·tana=20.00×0.5317=10.634( m).
∵CD=BE,∴BE=1.21(m).
∴AB=AE+BE=10.634+1.21=11.844≈11.8(m).
4.在Rt△ACD中,∠ACD=90°,∠CDA=90°-30°=60°.
∴AC=CD·tan60°=CD=300 (米) .
在Rt△BCD中,∠BDC=90°-60°=30°,∴BC=DC·tan30°=DC=100 (米).
故AB=200≈346. 4(米).
5.实践一:∵∠CED=∠AEB,∠CDE=∠ABE=90°.
∴△CED∽△AEB.∴ ,即,∴AB= 5.2米.
实践二:如(1)①②;(2)示意图如图;(3)CD=a,BD=b;(4)AB=a+b.(说明:本题答案不惟一).
6.AB′=12500cm=1250m,从而AB=≈1254(m).
又tanA==0.08,故∠A≈4°34′.
300
350
400
A
B
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
