数学:11.2全等三角形同步练习1(苏科版七年级下)
文档属性
| 名称 | 数学:11.2全等三角形同步练习1(苏科版七年级下) |  | |
| 格式 | rar | ||
| 文件大小 | 31.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 14:13:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学:11.2全等三角形同步练习(苏科版七年级下)
【基础演练】
一、填空题
1.如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=___ __cm,∠B=_ __.
2.如图,若△ACB≌△AED,且∠B=35°,∠C=48°,则∠EAD=___ __.
3.如图,△ABC绕点A旋转后与△ADE完全重合,则△ABC≌△_______,那么两个三角形的对应边为__ ___,__ ___,___ __,对应角为____ __,____ ___,___ ____.
4. 如图,把△ABC沿直线BC翻折180°到△DBC,那么△ABC≌△______;若△ABC的面积为2,那么△BDC的面积为______ ____.
二、选择题
5.下列说法:①全等三角形的形状相同,大小相等.②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长,面积分别相等;⑤所有的等边三角形都是全等三角形.其中正确的说法有( )
A.5个 B.4个 C.3个 D.1个
6. 如图,若△ABC≌△DEF,则∠E等于( )
A. 30° B. 50° C. 60° D. 100°
7. 已知△ABC≌△A B C ,且△ABC的周长为20,AB=8,BC=5,则A C 等于( )
A. 5 B. 6 C. 7 D. 8
8. △ABC与△DFE是全等三角形,A与D对应,B与F对应,则按标有字母的线段计算,图中相等的线段有( )
A. 1组 B. 2组 C. 3组 D. 4组
三、解答题
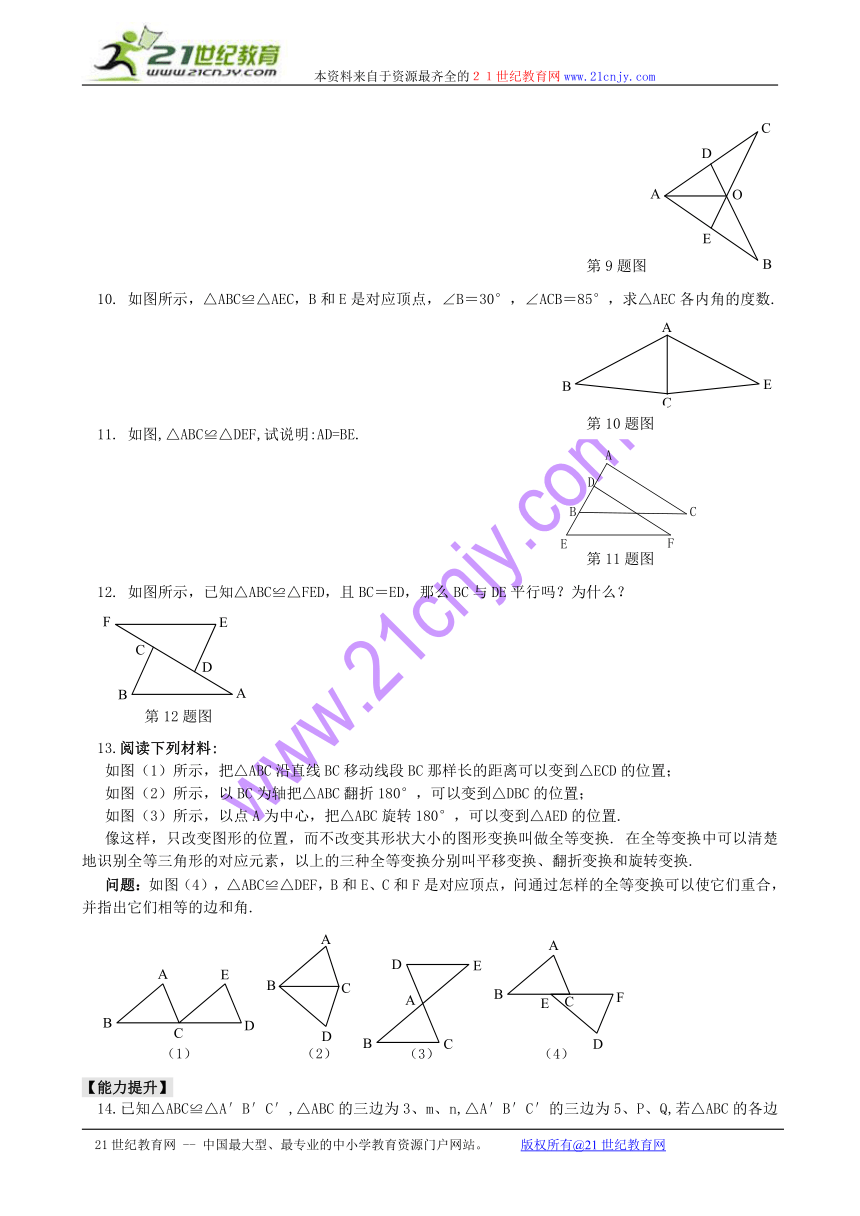
9. 如图所示,已知△ABD≌△ACE,∠B=∠C,试指出这两个三角形的对应边和对应角.
10. 如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
11. 如图,△ABC≌△DEF,试说明:AD=BE.
12. 如图所示,已知△ABC≌△FED,且BC=ED,那么BC与DE平行吗?为什么?
13.阅读下列材料:
如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;
如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.
【能力提升】
14.已知△ABC≌△A′B′C′,△ABC的三边为3、m、n,△A′B′C′的三边为5、P、Q,若△ABC的各边都是整数,则m+n+p+q的最大值为__________.
15. 如图△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明, 若不相等说出为什么
16.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
参考答案
1.3, 64°;2.97°;3.△ADE,AB和AD,AC和AE,BC和DE,∠B和∠D,∠C和∠E,∠BAC和∠DAE;4. DBC,2.
5.B;6.D;7. C;8. D.
三、解答题
9.解:对应边有:AB和AC,AD和AE,BD和CE;
对应角有:∠BAD=∠CAE,∠ADB=∠AEC,∠B=∠C.
10.解:∵△ABC≌△AEC,
∴∠B=∠E,∠BAC=∠EAC,∠ACB=∠ACE.
∵∠B=30°,∠ACB=85°,
∴∠E=30°,∠ACE=85°,
∴∠EAC=65°.
11. 解:∵△ABC≌△DEF,
∴AB=DE.
∴AB-BD=DE-BD.
∴AD=BE.
12. 如图所示,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?
解:∵△ABC≌△FED,
∴∠BCD=∠EDC.
∴BC∥DE.
13. 把△DEF沿EF翻折180°,再将翻转后的三角形沿CB(向左)方向平移,使E与B点重合,则△ABC与△DEF重合或旋转变换,AB=DF,AC=DE,BC=EF,∠A=∠D,∠B=∠F,∠ACB=∠DEF.
14.22.
15.解:∠1=∠2.
∵△ABC≌△EBD,
∴∠A=∠E.
在△AOF和△EOB中,
∵∠A=∠E,∠AOF=∠EOB,
∴∠1=∠2.
16.解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°, ∴∠ABC=25°. ∴∠CAB=50°.
∴∠DFB=∠DAB+∠ABC=50°+20°+25°=95°.∠AGB=105°-70°=35°.
第1题图
第2题图
第3题图
第4题图
第4题图
第9题图
第10题图
第11题图
第12题图
第15题图
第16题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学:11.2全等三角形同步练习(苏科版七年级下)
【基础演练】
一、填空题
1.如图,若△ABC≌△EFC,且CF=3cm,∠EFC=64°,则BC=___ __cm,∠B=_ __.
2.如图,若△ACB≌△AED,且∠B=35°,∠C=48°,则∠EAD=___ __.
3.如图,△ABC绕点A旋转后与△ADE完全重合,则△ABC≌△_______,那么两个三角形的对应边为__ ___,__ ___,___ __,对应角为____ __,____ ___,___ ____.
4. 如图,把△ABC沿直线BC翻折180°到△DBC,那么△ABC≌△______;若△ABC的面积为2,那么△BDC的面积为______ ____.
二、选择题
5.下列说法:①全等三角形的形状相同,大小相等.②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长,面积分别相等;⑤所有的等边三角形都是全等三角形.其中正确的说法有( )
A.5个 B.4个 C.3个 D.1个
6. 如图,若△ABC≌△DEF,则∠E等于( )
A. 30° B. 50° C. 60° D. 100°
7. 已知△ABC≌△A B C ,且△ABC的周长为20,AB=8,BC=5,则A C 等于( )
A. 5 B. 6 C. 7 D. 8
8. △ABC与△DFE是全等三角形,A与D对应,B与F对应,则按标有字母的线段计算,图中相等的线段有( )
A. 1组 B. 2组 C. 3组 D. 4组
三、解答题
9. 如图所示,已知△ABD≌△ACE,∠B=∠C,试指出这两个三角形的对应边和对应角.
10. 如图所示,△ABC≌△AEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求△AEC各内角的度数.
11. 如图,△ABC≌△DEF,试说明:AD=BE.
12. 如图所示,已知△ABC≌△FED,且BC=ED,那么BC与DE平行吗?为什么?
13.阅读下列材料:
如图(1)所示,把△ABC沿直线BC移动线段BC那样长的距离可以变到△ECD的位置;
如图(2)所示,以BC为轴把△ABC翻折180°,可以变到△DBC的位置;
如图(3)所示,以点A为中心,把△ABC旋转180°,可以变到△AED的位置.
像这样,只改变图形的位置,而不改变其形状大小的图形变换叫做全等变换. 在全等变换中可以清楚地识别全等三角形的对应元素,以上的三种全等变换分别叫平移变换、翻折变换和旋转变换.
问题:如图(4),△ABC≌△DEF,B和E、C和F是对应顶点,问通过怎样的全等变换可以使它们重合,并指出它们相等的边和角.
【能力提升】
14.已知△ABC≌△A′B′C′,△ABC的三边为3、m、n,△A′B′C′的三边为5、P、Q,若△ABC的各边都是整数,则m+n+p+q的最大值为__________.
15. 如图△ABC≌△EBD,问∠1与∠2相等吗 若相等请证明, 若不相等说出为什么
16.如图,已知△ABC≌△ADE,BC的边长线交AD于F,交AE于G,∠ACB=105°,∠CAD=10°,∠ADE=25°,求∠DFB和∠AGB的度数.
参考答案
1.3, 64°;2.97°;3.△ADE,AB和AD,AC和AE,BC和DE,∠B和∠D,∠C和∠E,∠BAC和∠DAE;4. DBC,2.
5.B;6.D;7. C;8. D.
三、解答题
9.解:对应边有:AB和AC,AD和AE,BD和CE;
对应角有:∠BAD=∠CAE,∠ADB=∠AEC,∠B=∠C.
10.解:∵△ABC≌△AEC,
∴∠B=∠E,∠BAC=∠EAC,∠ACB=∠ACE.
∵∠B=30°,∠ACB=85°,
∴∠E=30°,∠ACE=85°,
∴∠EAC=65°.
11. 解:∵△ABC≌△DEF,
∴AB=DE.
∴AB-BD=DE-BD.
∴AD=BE.
12. 如图所示,已知△ABC≌△FED,且BC=ED,那么AB与EF平行吗?为什么?
解:∵△ABC≌△FED,
∴∠BCD=∠EDC.
∴BC∥DE.
13. 把△DEF沿EF翻折180°,再将翻转后的三角形沿CB(向左)方向平移,使E与B点重合,则△ABC与△DEF重合或旋转变换,AB=DF,AC=DE,BC=EF,∠A=∠D,∠B=∠F,∠ACB=∠DEF.
14.22.
15.解:∠1=∠2.
∵△ABC≌△EBD,
∴∠A=∠E.
在△AOF和△EOB中,
∵∠A=∠E,∠AOF=∠EOB,
∴∠1=∠2.
16.解:∵△ABC≌△ADE,
∴∠ACB=∠AED,∠ABC=∠ADE,∠CAB=∠EAD.
∵∠ADE=25°, ∴∠ABC=25°. ∴∠CAB=50°.
∴∠DFB=∠DAB+∠ABC=50°+20°+25°=95°.∠AGB=105°-70°=35°.
第1题图
第2题图
第3题图
第4题图
第4题图
第9题图
第10题图
第11题图
第12题图
第15题图
第16题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
