北京师范大学附属中学2023-2024学年下学期统练八数学试题(PDF版,含解析)
文档属性
| 名称 | 北京师范大学附属中学2023-2024学年下学期统练八数学试题(PDF版,含解析) |  | |
| 格式 | |||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 15:16:27 | ||
图片预览




文档简介
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
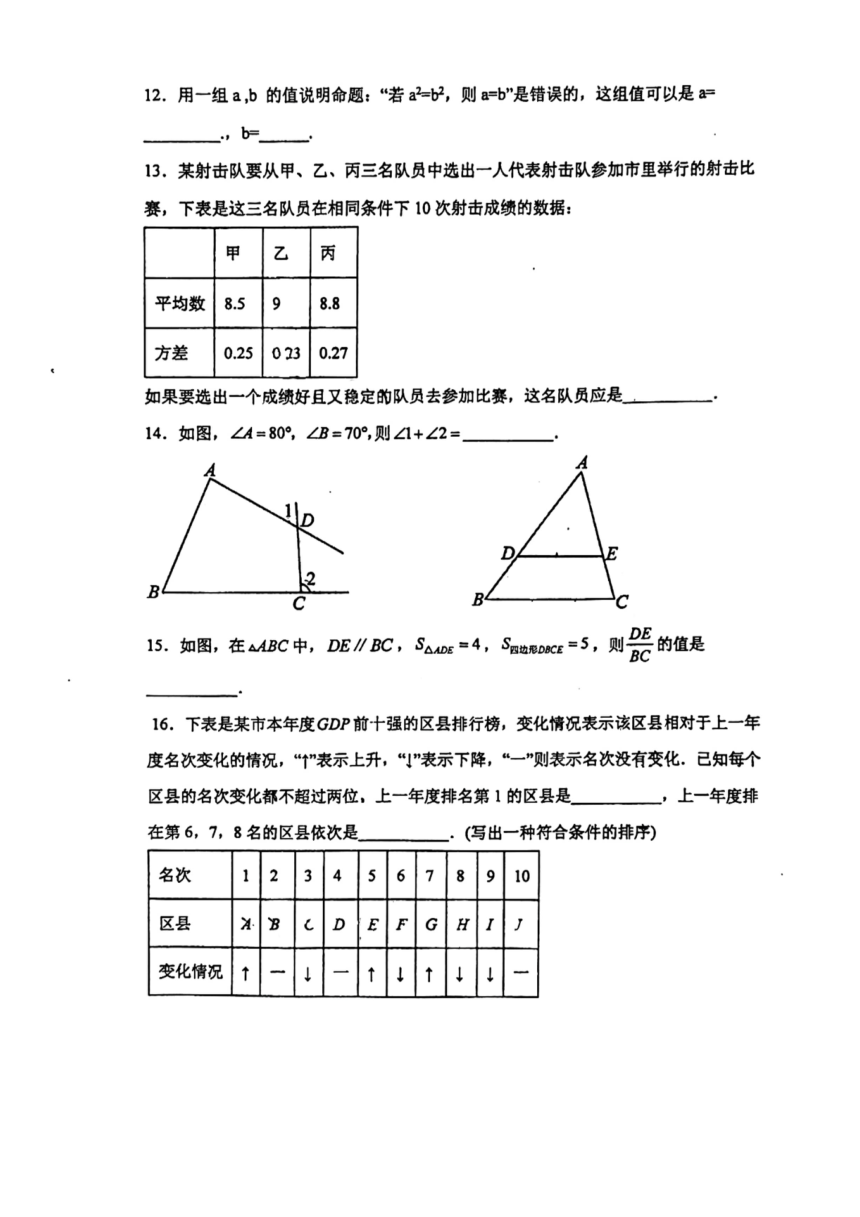
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
参考答案
第一部分选择题
一、选择题(共 16分,每题 2分)第 1-8题均有四个选项,符合题意的选项只有一个.
1. 【答案】B
【分析】根据几何体的主视图和左视图都是长方形,可判断该几何体是柱体,进而根据俯视图的形状,可
判断柱体底面形状,得到答案.
【详解】由几何体的主视图和左视图都是长方形,
故该几何体是柱体,
又因为俯视图是三角形,
故该几何体是三棱柱.
故选:B.
2. 【答案】C
【分析】科学记数法的表示形式为 a 10n 的形式,其中1 a 10,n 为整数.确定 n 的值时,要看把
原数变成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值 10 时,n 是
正数;当原数的绝对值<1时,n 是负数.
【详解】解:将 1040000000 用科学记数法表示为:1.04 109 .
故选:C.
1 a 10,n 为整数,表示时关键要正确确定 a 的值以及 n 的值.
3. 【答案】C
【分析】根据加减消元法进行求解即可.
x + y = 3①
【详解】解: ,
3x y = 5②
①+②,得, 4x = 8,
解得, x = 2,
把 x = 2 代入①得, 2+ y = 3,
解得, y =1,
x = 2,
∴方程组的解为:
y =1
故选:C
【点睛】本题主要考查解二元一次方程组,解答的关键是对解二元一次方程组的方法的掌握.
4. 【答案】B
【分析】根据算术平方根的定义估算无理数 3 、 14 的大小即可.
第1页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【详解】解: 1 3 2,3 14 4,
比 3 大且比 14 小的整数有:2 和 3,
故选:B.
5. 【答案】D
1
【分析】首先根据角平分线计算出 BEG = BEF = 58 ,再根据两直线平行内错角相等得出 EGC
2
的大小即可.
【详解】解: BEF =116 , EG 平分 BEF ,
1 1
BEG = FEG = BEF = 116 = 58 ,
2 2
AB∥CD ,
EGC = BEG = 58 ,
故选:D .
6. 【答案】C
【分析】先利用树状图法得出两次摸球所有可能的结果,进而利用概率的计算公式求解即可.
【详解】画树状图得所有可能出现的结果数为∶
共有 12 种等可能的结果,两次摸出小球的颜色相同的有 6 种情况,
6 1
两次摸出小球的颜色相同的概率是: = .
12 2
故选 C.
7. 【答案】D
1
【分析】由数轴可知 0 a 1 ,移项和两边除以 a 分别得到 a 0 , 1 ,两边同时乘以 a 得到
a
2 1
0 a2 a ,从而得到 a 0 a a 1 ,由此选出答案.
a
【详解】解:由数轴可知: 0 a 1,
1
∴ a 0 , 1.
a
又∵ 0 a 1,
∴两边乘以 a得:0 a2 a ,
第2页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
a 0 a2
1
∴ a 1 ,
a
1 1
∴a, a, a 2 , 中,最大的是 .
a a
故选:D
8. 【答案】A
【分析】分别求出三个问题中变量 y 与变量 x之间的函数关系式即可得到答案.
1463
【详解】解:①由平均速度等于路程除以时间得: y = ,符合题意;
x
1.68 104 16800
②由人均面积等于总面积除以总人口得: y = ,即 y = ,符合题意;
x x
1 1 1
③由加满汽油后开了 200km时,油箱中汽油大约消耗了 ,可知每公里油耗为: 50 200 = (L),
4 4 16
再由油箱中的剩油量等于油箱容量减去耗油量,耗油量等于每公里油耗乘以加满汽油后汽车行驶的路程得:
1
y = 50 x,不符合题意;
16
综上分析可知,变量 y 与变量 x 之间的函数关系可以用该图象表示的是①②.
故选:A.
第二部分非选择题
二、填空题(共 16分,每题 2分)
9. 【答案】 x 2
【分析】根据分式有意义的条件即分母不为 0 可直接进行求解.
【详解】解:由题意可得:
x 2 0,
∴ x 2,
故答案为: x 2.
10. 【答案】m 1
m 1
【分析】根据反比例函数 y = 的图象位于第二、四象限,可以得到m 1 0,然后求解即可.
x
m 1
【详解】解: 反比例函数 y = 的图象位于第二、四象限,
x
m 1 0 ,
解得:m 1,
故答案为:m 1.
4
11. 【答案】
3
第3页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【分析】取点 B (3,0),则 AB ⊥ x轴于 B,根据点 A 的坐标求出OB 和 AB ,根据锐角正切函数的定义求
出即可.
【详解】取点 B (3,0),则 AB ⊥ x轴于 B,
∵点 A 的坐标为(3,4),
∴OB = 3,AB = 4 ,
AB 4
tan = = .
OB 3
4
故答案为: .
3
12. 【答案】 ①. 1 ②. 1
【分析】通过 a 取 1,b 取-1 可说明命题“若 a2=b2,则 a=b”是错误的.
【详解】解:当 a=1,b=-1 时,满足 a2=b2,但 a≠b.故命题错误.
故答案为 1,-1(答案不唯一).
13. 【答案】乙
【分析】根据方差越小越稳定和平均数决策即可.
【详解】解:∵乙的平均数最大,方差最小,即乙的成绩好且状态稳定,
∴这名队员应是乙.
故答案是:乙.
14. 【答案】150
【分析】延长 AD, BC 相交于点 E, 由三角形内角和定理求出 E = 30 , 2+ EDC =150 ,由对顶角相等
可得 EDC = 1, 从而可得结论.
【详解】解:延长 AD, BC 相交于点 E, 如图,
∴ A+ B + E =180 ,
第4页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
又 A = 80 , B = 70 ,
∴ E =180 A B =18 80 70 = 30 ,
又 2+ EDC + E =180 ,
∴ 2+ EDC =180 E =180 30 =150 ,
又 EDC = 1,
∴ 1+ 2 =150 ,
故答案为:150 .
2
15. 【答案】
3
【分析】先证明 ADE ABC ,然后利用相似三角形的性质求解.
【详解】解:∵ DE∥BC ,
∴ ADE ABC ,
2
S
∴ ADE
DE 4
,
S ABC BC 4 5
DE 2
∴ = ,
BC 3
2
故答案为: .
3
16. 【答案】 ①. C ②. E、H、I 或 H、E、I. (二者之一即可)
【分析】①C 地GDP名次下降,只能是第一名下降而来的,即上一年度排名第 1 的区县是 C;
② F 地GDP名次下降,上一年度 F 地排第五,G 地GDP名次上升,上一年度 G 地排第九,E 地本年度
GDP排第五,名次上升,上一年度可能是排第六或者第七,然后分类讨论即可.
【详解】解:①∵A 地GDP名次上升,每个区县的名次变化都不超过两位,B 地GDP 名次无变化,
∴只能是第三名上升而来的,即原来 A 地原来名次是第三名;
同理,C 地GDP名次下降,只能是第一名下降而来的;
∴上一年度排名第 1 的区县是 C,上一年度排名前四名依次是C、B、A、D ;
②F 地GDP名次下降,只能是从第五名下降,即上一年度 F 地排第五,
同理,G 地GDP名次上升,只能是从第九名上升,即上一年度 G 地排第九,
∵E 地本年度GDP排第五,名次上升,每个区县的名次变化都不超过两位,
∴E 地上一年度可能是排第六或者第七
(i)若 E 地上一年度是排第六,即 E 地和 F 地的排名交换,
∴H 地上一年度是排第七,I 地上一年度是排第八,
∴上一年度排名从前往后依次是:C、B、A、D、F、E、H、I、G、J ;
(ii)若 E 地上一年度是排第七,
第5页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∵H 地本年度GDP排第八,GDP名次下降,现在上一年度未确定的只有第六和第八,
∴H 地上一年度是排第六,I 地上一年度是排第八
∴上一年度排名从前往后依次是:C、B、A、D、F、H、E、I、G、J ;
∴上一年度排在第 6,7,8 名的区县依次是 E、H、I 或 H、E、I .
故答案为: C; E、H、I 或 H、E、I (二者之一即可).
三、解答题(共 68分,第 17-20题,每题 5分,第 21-22题,每题 6分,第 23题 5分,第
24题 6分,第 25题 5分,第 26题 6分,第 27-28题,每题 7分)解答应写出文字说明、演
算步骤或证明过程.
17. 【答案】1
【解析】
【分析】利用特殊角的三角函数值、负整数指数幂、绝对值的性质逐项计算,即可求解.
1
1
【详解】解: 8 4cos 45 + 2
3
2
= 2 2 4 +3 2
2
= 2 2 2 2 + 3 2
=1.
18. 【答案】 1 x 2,1,2
【分析】根据解一元一次不等式的步骤即可解答.
x 1
2x +1 ①
【详解】解: 2 ,
3x 1 5②
由①得: x 1,
由②得: x 2 ,
∴原不等式的解集为 1 x 2;
∴原不等式所有正整数解为:1,2;
19. 【答案】(1)见解析 (2)两组对边分别相等的四边形是平行四边形;90;有一个内角是直角的平
行四边形是矩形.
【解析】
【分析】(1)按照步骤操作即可;
(2)根据矩形的判定定理推导,填空即可.
【小问 1 详解】
解:补全图形如下:
第6页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【小问 2 详解】
证明:∵ AD = BC = b, AB = DC = a,
∴四边形 ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
∵直线m ⊥ l ,
∴ ABC = 90 ,
∴四边形 ABCD 是矩形(有一个内角是直角的平行四边形是矩形).
故答案是:两组对边分别相等的四边形是平行四边形;90;有一个内角是直角的平行四边形是矩形.
20. 【答案】化简为: a2 + a,结果值为:5
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据已知等式可得答案.
1 a 1
【详解】解: a
a a2
a2 1 a2
=
a a 1
(a + 1) (a 1) a2
=
a a 1
= a2 + a ,
a2 + a 5 = 0
a2 + a = 5
1 a 1
a = a
2 + a = 5.
2
a a
21. 【答案】m =1, x1 = 2 , x2 =1
2
【分析】先根据根的判别式的意义得到 = ( 3) 4(m+1) 0 ,解不等式,从而得到正整数 m 的值,代
入原方程,然后利用因式分解法解方程即可.
2
【详解】根据题意得Δ = ( 3) 4(m+1) 0
5
解得m
4
所以正整数 m 的值为 1
代入原方程得 x2 3x + 2 = 0
第7页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
即 (x 2)(x 1) = 0
∴ x1 = 2 , x2 =1
22. 【答案】(1)见解析 (2)OE = 37
【分析】(1)根据矩形的对角线相等可得 AC = BD,对边平行可得 AD∥BC ,再证明出四边形
ADEC 是平行四边形,根据平行四边形的对边相等可得 AC = DE ,从而得证;
(2)如图,过点 O 作OF ⊥ CD 于点 F,欲求OE ,只需在直角 OEF 中求得OF、FE 的值即可.结合
三角形中位线求得OF ,结合矩形、平行四边形的性质以及勾股定理求得OE 即可.
【小问 1 详解】
∵四边形 ABCD是矩形,
∴ AC = BD,AD∥BC ,
又∵ DE∥ AC ,
∴四边形 ADEC 是平行四边形,
∴ AC = DE ,
∴ BD = DE ;
【小问 2 详解】
如图,过点 O 作OF ⊥ BC 于点 F,
∵四边形 ABCD是矩形,
∴ AC BD,点 O 是 AC, BD 的中点, AD = BC = 4,
1 1
∴OC = AC,OB = BD,
2 2
∴OC =OB,
1
∴CF = BF = BC = 2,
2
∴ F 点是 BC 的中点,
∴OF 是△BCD 的中位线,
1
∴OF = CD =1,
2
又∵四边形 ADEC 是平行四边形,
∴CE = AD = 4, .
第8页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∴ EF = CF +CE = 2+ 4 = 6.
在Rt△OEF 中,由勾股定理可得:OE = OF 2 + EF 2 = 12 + 62 = 37 .
【点睛】本题考查了矩形的性质,平行四边形的判定与性质,熟记各性质并求出四边形 ADEC 是平行四
边形是解题的关键.
23. 【答案】(1)见解析 (2)88.5 分;94 分
(3)1900 份
【分析】(1)用 20 减去第一、二、四、五组的频数即可得到第三组( 70 x 80)的频数,进而可补全
频数分布直方图;
(2)根据中位数和众数的定义求解即可;
(3)用样本百分比估计总体数量即可.
【小问 1 详解】
第三组( 70 x 80)的频数为: 20 1 1 7 9 = 2 ,
补全图形如下:
【小问 2 详解】
∵20 个数据按大小顺序排列,最中间的两个数据是第 10 和 11 个,
∴A 小区参加有奖问答活动的 20 名居民成绩的数据的中位数在80 x 90 这一组内的第 6 和 7 个数据的
88+89
平均数,即 =88.5;
2
B 小区参加有奖问答活动的 20 名居民成绩中出现次数最多的是 94 分,出现 4 次,
故 B 小区参加有奖问答活动的 20 名居民成绩中众数是 94 分,
故答案为:88.5 分;94 分;
【小问 3 详解】
9 10
2000+ 200=1900(份)
20 20
答:估计这两个小区的居委会一共需要准备 1900 份小奖品
24. 【答案】(1)见解析;
(2)见解析
第9页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【分析】(1)根据直径所对的圆周角是直角及菱形的性质得到点M 是 BD 的中点即可解答;
(2)根据菱形的性质及全等三角形的判定得到 DBE≌ DBF ,再根据全等三角形的性质得到
BFD = DEB = 90 ,最后利用四边形的内角和及切线的判定即可解答.
【小问 1 详解】
解:连接 AM ,
∵ AD 为 O 的直径,
∴ AMD = 90 ,
∴ AM ⊥ BD ,
∵四边形 ABCD是菱形,
∴ AD = AB ,
∴点M 是 BD的中点,
∴ DM = BM ;
【小问 2 详解】
解:连接 DE ,
∵四边形 ABCD是菱形,
∴ DBE = DBF , DAB + ABC =180 ,
∴在 DBE 和 DBF ,
BE = BF
DBE = DBF ,
BD = BD
∴ DBE≌ DBF (SAS ),
∴ DEB = DFB ,
∵ AD 是 O 的直径,
∴ AED = DEB = 90 ,
∴ BFD = DEB = 90 ,
第10页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∵ DAB + ABC =180 ,
∴在四边形 ABFD 中, ADF + DFB =180 ,
∴ ADF = 90 ,
∴ AD ⊥ DF ,
∴ DF 是 O 的切线.
25. 【答案】(1)1, 2
5
(2)①1;② 2 xP
2
【分析】(1)先根据直线的解析式可求 a 的值,从而可得点 A 的坐标,再将点 A 坐标代入反比例函数的
解析式可得 k 的值;
(2)①先求出点 P 坐标,再根据反比例函数的解析式求出点 B 、C 坐标,然后结合函数图像、整点的定
义即可得;②由图可知点 P 不可能在点 A 下方,故点 P 在点 A 上方,结合函数图像列出不等式组求解即
可.
【小问 1 详解】
k
解: 函数 y = (x 0)的图像与一次函数 y = 2x 的图像交于点 A(a, 2),
x
2 = 2 a ,即 a =1,
A(1, 2),
( k
k
将 A 1, 2)代入反比例函数 y = (x 0)中, 2 = 解得: k = 2,
x 1
故答案为: a =1, k = 2;
【小问 2 详解】
2
①由(1)可知反比例函数解析式为 y = (x 0),
x
点 P 是射线OA上一点, P 的横坐标是 2 ,
y = 2 2 = 4
P (2,4)
2
将 x = 2 代入 y = (x 0),得 y =1
x
2 1
将 y = 4 代入 y = (x 0),得 x =
x 2
k
点 P 与 x轴, y 轴的垂线交函数 y = (x 0)的图像于点 B ,C ,
x
1
B (2,1),C ,4 ,
2
如图:
第11页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
结合函数图像可知,区域W 内有1个整数点;
②区域W 内恰有5个整点,由图可知点 P 只能位于A 的上方如图:
y 5
如图,当 P 的纵坐标为5时,横坐标为 x = = ,
2 2
5
结合图像可知,当 2 xP 时,区域内有5个整数点.
2
26. 【答案】(1) y1 y2 ,理由见解析
(2)m 2
【解析】
【分析】(1)当m = 2时,3 x2 5 ,将抛物线解析式化为顶点式,得到对称轴,根据 x x1, 2 的大小
判断与对称轴的距离,结合 a<0,即可得出答案;
第12页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
(2)根据题意可知满足 y1 = y2 ,即x 与x1 2关于对称轴 x =1对称,当 1 x1 2时,则x 2的最小值要
比 x1 = 2 时的对称点 0 小,x 2的最大值要比 x1 = 1时的对称点 3 大,解不等式组即可.
【小问 1 详解】
y1 y2 ;
2
理由:∵ y = ax2 2ax +8 = a (x 1) +8 a,
∴抛物线的对称轴是直线 x =1
当m = 2时,3 x2 5
∵ 1 x1 2,3 x2 5 ,对称轴是直线 x =1
∴x 比x 离对称轴近 1 2
∵ a<0,抛物线开口向下
∴ y1 y2
【小问 2 详解】
∵1 m x2 m + 7
∴1 m m + 7
解得m 3①
∵存在 x1, x2 ,满足 y1 = y2 ,且 1 x1 2
∴1 m 3
解得m 2②
综上,m 的取值范围是m 2
27. (1)
①依题意补全图形如图所示:
证明:∵AC绕点逆时针旋转 180°-α得到线段 CE
∴ AC = CE ,
∵点 F 是 DE的中点,
∴ DF = EF ,
∵点 C 与点 G 关于点 F 对称,
∴CF =GF ,
又∵ DFG = EFC ,
∴ DFG EFC ,
∴ DG = CE ,
∴ AC = DG ;
第13页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
②证明:∵边 AB 绕点 B顺时针旋转α(<0°α<180°)得到线段 BD,
∴ BD = BA,
设 ACB = x, ABC = y,则 BAC =180 (x + y) .
∴在四边形 BDEC 中,
BDE + CED = 360 DBC BCE =180 (x + y)
∵ DFG EFC ,
∴ GDF = CEF ;
∴ BDG = BDE + GDF =180 (x + y)
∴ BDG = BAC ;
∴ BDG BAC ,
∴ DGB = ACB ;
3
(2) FH = BC
4
28. 【答案】(1)2 2 ,3
(2)b 的取值范围是 3 b 6 或 6 b 3 ;
3 7
(3)2 t +1
2 2
【分析】(1)设经过点 M 的直线与 O 交于 E、F 两点,过点 O 作OH ⊥ EF 于 H,连接OM,OE ,利
用垂径定理得到 EF = 2EH ,由勾股定理可得当OH 最大时, EH 最小,即此时 EF 最小,求出
OM = 2 ,再由OH OM ,得到当点 H 与点 M 重合时,OH 有最大值 2 ,即可求出 EF 的最小值为
2 2 ,则被圆 O 截得的弦长取值范围为 2 2 x 4 ,再由被圆 O 截得的弦长为 3 的弦有 2 条,被圆 O
截得的弦长为 4 的弦只有 1 条,可得点 M 关于圆 O 的特征值为 3;
(2)根据题意得,关于圆 O的特征值为 4 的所有点都在以 O为圆心, 3 为半径的圆周上,分当b 0时和
当b 0时,两种情况讨论即可求解;
(3)由于同一平面内,对于任意一点 Q,经过 O、Q 的直线与圆 O 截得的弦(直径)都为 4,则点 Q 关
r =1 r = 2
于圆 O 的特征值不可能为 0,由此可得 rs 0,则 或 ;经过点 S 且弦长为 4(最长弦)的直
s = 2 s =1
第14页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
7
线有 1 条,弦长为 3(最短弦)的直线有 1 条,由(2)可知点 S 一定在以 O 为圆心,以 为半径的圆
2
3
上,同理点 R 一定在以 T 为圆心,以 为半径的圆上,则当满足以 O 为圆心,2 为半径的圆与以 T 为圆
2
3 7
心, 为半径的圆有交点,且同时满足以 O 为圆心, 为半径的圆与以 T 为圆心,1 为半径的圆有交
2 2
点时 t 的值符合题意,由此求解即可.
【小问 1 详解】
解:设经过点 M 的直线与 O 交于 E、F 两点,过点 O 作OH ⊥ EF 于 H,连接OM,OE ,
∴ EF = 2EH ,
在Rt△OEH 中,由勾股定理得EH = OE 2 OH 2 = 4 OH 2 ,
∴当OH 最大时, EH 最小,即此时 EF 最小,
∵点 M 的坐标为 (1,1),
∴OM = 12 +12 = 2 ,
又∵OH OM ,
∴当点 H 与点 M 重合时,OH 有最大值 2 ,
2
∴此时 EH 有最小值 4 ( 2 ) = 2 ,
∴ EF 的最小值为 2 2
∵过点 M 的直线被圆 O 截得的弦长的最大值为 4(直径),
∴被圆 O 截得的弦长取值范围为 2 2 x 4 ,
∴被圆 O 截得的弦长为正整数的只有是 3 或 4,
∵被圆 O 截得的弦长为 3 的弦有 2 条,被圆 O 截得的弦长为 4 的弦只有 1 条,
∴点 M 关于圆 O 的特征值为 3,
故答案为: 2 2 ,3;
【小问 2 详解】
第15页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
解:设点 G 是圆 O 的特征值为 4 的点,
由(1)可知经过一点 G 且弦长为 4(最长弦)的直线有 1 条,弦长为 3 的直线有 2 条,
∵特征值要保证为 4,
∴经过点 G 且弦长为 2 的直线有且只有 1 条,
∴经过点 G 的直线被圆 O 截得的弦长的最小值为 2,
∵ 22 12 = 3 ,
∴由(1)可知,关于圆 O 的特征值为 4 的所有点都在以 O 为圆心, 3 为半径的圆周上,
∵直线 y = x + b分别与 x,y 轴交于点 A,B,
∴ A( b,0), B (0,b),
∴OA =OB = b,
∴ OBH = 45
当b 0时,
∵线段 AB 上总存在关于圆 O 的特征值为 4 的点,
∴线段 AB 与以 O 为圆心, 3 为半径的圆有交点,
当线段 AB 与以 O 为圆心, 3 为半径的圆相切时,将切点设为 H,连接 OH,则OH = 3 ,
∴OB = 2OH = 6 ,
∴b1 = 6 ,
将以 O 为圆心, 3 为半径的圆与 y 轴正半轴的交点记为 B1,则OB1 = 3 ,
当线段 AB 与以 O 为圆心, 3 为半径的圆相交,且过点 B1时,可得b = 3 , 2
∴ 3 b 6 ;
同理可求当b 0时, 6 b 3 ;
综上,b 的取值范围是 3 b 6 或 6 b 3 ;
【小问 3 详解】
:∵同一平面内,对于任意一点 Q,经过 O、Q 的直线与圆 O 截得的弦(直径)都为 4,
∴点 Q 关于圆 O 的特征值不可能为 0,
第16页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∴ rs 0,
∵ r + s = 3,且 r、s 都是整数,
r =1 r = 2
∴ 或 ;
s = 2 s =1
r =1
当 时,
s = 2
∴经过点 S 且弦长为 4(最长弦)的直线有 1 条,弦长为 3(最短弦)的直线有 1 条,
2
3 7
∴由(2)可知点 S 一定在以 O 为圆心,以 22 = 为半径的圆上,
2 2
r = 2 2 1 3
同理当 时,点 R 一定在以 T 为圆心,以 12 = 为半径的圆上,
s =1 2 2
3
∴当满足以 O 为圆心,2 为半径的圆与以 T 为圆心, 为半径的圆有交点,且同时满足以 O 为圆心,
2
7
为半径的圆与以 T 为圆心,1 为半径的圆有交点时 t 的值符合题意;
2
如图 3-1 所示,
3 7
当以 O 为圆心, 为半径的圆与以 T 为圆心,1 为半径的圆外切时,此时 t1 = +1;
2 2
3 3
如图 3-2 所示,当以 O 为圆心,2 为半径的圆与以 T 为圆心, 为半径的圆外切时,此时 t2 = 2 ;
2 2
3 7
综上所述,当2 t +1时,存在点 R,S,使得 r + s = 3.
2 2
第17页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
第18页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
{#{QQABAQAAggggAJJAAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
参考答案
第一部分选择题
一、选择题(共 16分,每题 2分)第 1-8题均有四个选项,符合题意的选项只有一个.
1. 【答案】B
【分析】根据几何体的主视图和左视图都是长方形,可判断该几何体是柱体,进而根据俯视图的形状,可
判断柱体底面形状,得到答案.
【详解】由几何体的主视图和左视图都是长方形,
故该几何体是柱体,
又因为俯视图是三角形,
故该几何体是三棱柱.
故选:B.
2. 【答案】C
【分析】科学记数法的表示形式为 a 10n 的形式,其中1 a 10,n 为整数.确定 n 的值时,要看把
原数变成 a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值 10 时,n 是
正数;当原数的绝对值<1时,n 是负数.
【详解】解:将 1040000000 用科学记数法表示为:1.04 109 .
故选:C.
1 a 10,n 为整数,表示时关键要正确确定 a 的值以及 n 的值.
3. 【答案】C
【分析】根据加减消元法进行求解即可.
x + y = 3①
【详解】解: ,
3x y = 5②
①+②,得, 4x = 8,
解得, x = 2,
把 x = 2 代入①得, 2+ y = 3,
解得, y =1,
x = 2,
∴方程组的解为:
y =1
故选:C
【点睛】本题主要考查解二元一次方程组,解答的关键是对解二元一次方程组的方法的掌握.
4. 【答案】B
【分析】根据算术平方根的定义估算无理数 3 、 14 的大小即可.
第1页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【详解】解: 1 3 2,3 14 4,
比 3 大且比 14 小的整数有:2 和 3,
故选:B.
5. 【答案】D
1
【分析】首先根据角平分线计算出 BEG = BEF = 58 ,再根据两直线平行内错角相等得出 EGC
2
的大小即可.
【详解】解: BEF =116 , EG 平分 BEF ,
1 1
BEG = FEG = BEF = 116 = 58 ,
2 2
AB∥CD ,
EGC = BEG = 58 ,
故选:D .
6. 【答案】C
【分析】先利用树状图法得出两次摸球所有可能的结果,进而利用概率的计算公式求解即可.
【详解】画树状图得所有可能出现的结果数为∶
共有 12 种等可能的结果,两次摸出小球的颜色相同的有 6 种情况,
6 1
两次摸出小球的颜色相同的概率是: = .
12 2
故选 C.
7. 【答案】D
1
【分析】由数轴可知 0 a 1 ,移项和两边除以 a 分别得到 a 0 , 1 ,两边同时乘以 a 得到
a
2 1
0 a2 a ,从而得到 a 0 a a 1 ,由此选出答案.
a
【详解】解:由数轴可知: 0 a 1,
1
∴ a 0 , 1.
a
又∵ 0 a 1,
∴两边乘以 a得:0 a2 a ,
第2页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
a 0 a2
1
∴ a 1 ,
a
1 1
∴a, a, a 2 , 中,最大的是 .
a a
故选:D
8. 【答案】A
【分析】分别求出三个问题中变量 y 与变量 x之间的函数关系式即可得到答案.
1463
【详解】解:①由平均速度等于路程除以时间得: y = ,符合题意;
x
1.68 104 16800
②由人均面积等于总面积除以总人口得: y = ,即 y = ,符合题意;
x x
1 1 1
③由加满汽油后开了 200km时,油箱中汽油大约消耗了 ,可知每公里油耗为: 50 200 = (L),
4 4 16
再由油箱中的剩油量等于油箱容量减去耗油量,耗油量等于每公里油耗乘以加满汽油后汽车行驶的路程得:
1
y = 50 x,不符合题意;
16
综上分析可知,变量 y 与变量 x 之间的函数关系可以用该图象表示的是①②.
故选:A.
第二部分非选择题
二、填空题(共 16分,每题 2分)
9. 【答案】 x 2
【分析】根据分式有意义的条件即分母不为 0 可直接进行求解.
【详解】解:由题意可得:
x 2 0,
∴ x 2,
故答案为: x 2.
10. 【答案】m 1
m 1
【分析】根据反比例函数 y = 的图象位于第二、四象限,可以得到m 1 0,然后求解即可.
x
m 1
【详解】解: 反比例函数 y = 的图象位于第二、四象限,
x
m 1 0 ,
解得:m 1,
故答案为:m 1.
4
11. 【答案】
3
第3页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【分析】取点 B (3,0),则 AB ⊥ x轴于 B,根据点 A 的坐标求出OB 和 AB ,根据锐角正切函数的定义求
出即可.
【详解】取点 B (3,0),则 AB ⊥ x轴于 B,
∵点 A 的坐标为(3,4),
∴OB = 3,AB = 4 ,
AB 4
tan = = .
OB 3
4
故答案为: .
3
12. 【答案】 ①. 1 ②. 1
【分析】通过 a 取 1,b 取-1 可说明命题“若 a2=b2,则 a=b”是错误的.
【详解】解:当 a=1,b=-1 时,满足 a2=b2,但 a≠b.故命题错误.
故答案为 1,-1(答案不唯一).
13. 【答案】乙
【分析】根据方差越小越稳定和平均数决策即可.
【详解】解:∵乙的平均数最大,方差最小,即乙的成绩好且状态稳定,
∴这名队员应是乙.
故答案是:乙.
14. 【答案】150
【分析】延长 AD, BC 相交于点 E, 由三角形内角和定理求出 E = 30 , 2+ EDC =150 ,由对顶角相等
可得 EDC = 1, 从而可得结论.
【详解】解:延长 AD, BC 相交于点 E, 如图,
∴ A+ B + E =180 ,
第4页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
又 A = 80 , B = 70 ,
∴ E =180 A B =18 80 70 = 30 ,
又 2+ EDC + E =180 ,
∴ 2+ EDC =180 E =180 30 =150 ,
又 EDC = 1,
∴ 1+ 2 =150 ,
故答案为:150 .
2
15. 【答案】
3
【分析】先证明 ADE ABC ,然后利用相似三角形的性质求解.
【详解】解:∵ DE∥BC ,
∴ ADE ABC ,
2
S
∴ ADE
DE 4
,
S ABC BC 4 5
DE 2
∴ = ,
BC 3
2
故答案为: .
3
16. 【答案】 ①. C ②. E、H、I 或 H、E、I. (二者之一即可)
【分析】①C 地GDP名次下降,只能是第一名下降而来的,即上一年度排名第 1 的区县是 C;
② F 地GDP名次下降,上一年度 F 地排第五,G 地GDP名次上升,上一年度 G 地排第九,E 地本年度
GDP排第五,名次上升,上一年度可能是排第六或者第七,然后分类讨论即可.
【详解】解:①∵A 地GDP名次上升,每个区县的名次变化都不超过两位,B 地GDP 名次无变化,
∴只能是第三名上升而来的,即原来 A 地原来名次是第三名;
同理,C 地GDP名次下降,只能是第一名下降而来的;
∴上一年度排名第 1 的区县是 C,上一年度排名前四名依次是C、B、A、D ;
②F 地GDP名次下降,只能是从第五名下降,即上一年度 F 地排第五,
同理,G 地GDP名次上升,只能是从第九名上升,即上一年度 G 地排第九,
∵E 地本年度GDP排第五,名次上升,每个区县的名次变化都不超过两位,
∴E 地上一年度可能是排第六或者第七
(i)若 E 地上一年度是排第六,即 E 地和 F 地的排名交换,
∴H 地上一年度是排第七,I 地上一年度是排第八,
∴上一年度排名从前往后依次是:C、B、A、D、F、E、H、I、G、J ;
(ii)若 E 地上一年度是排第七,
第5页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∵H 地本年度GDP排第八,GDP名次下降,现在上一年度未确定的只有第六和第八,
∴H 地上一年度是排第六,I 地上一年度是排第八
∴上一年度排名从前往后依次是:C、B、A、D、F、H、E、I、G、J ;
∴上一年度排在第 6,7,8 名的区县依次是 E、H、I 或 H、E、I .
故答案为: C; E、H、I 或 H、E、I (二者之一即可).
三、解答题(共 68分,第 17-20题,每题 5分,第 21-22题,每题 6分,第 23题 5分,第
24题 6分,第 25题 5分,第 26题 6分,第 27-28题,每题 7分)解答应写出文字说明、演
算步骤或证明过程.
17. 【答案】1
【解析】
【分析】利用特殊角的三角函数值、负整数指数幂、绝对值的性质逐项计算,即可求解.
1
1
【详解】解: 8 4cos 45 + 2
3
2
= 2 2 4 +3 2
2
= 2 2 2 2 + 3 2
=1.
18. 【答案】 1 x 2,1,2
【分析】根据解一元一次不等式的步骤即可解答.
x 1
2x +1 ①
【详解】解: 2 ,
3x 1 5②
由①得: x 1,
由②得: x 2 ,
∴原不等式的解集为 1 x 2;
∴原不等式所有正整数解为:1,2;
19. 【答案】(1)见解析 (2)两组对边分别相等的四边形是平行四边形;90;有一个内角是直角的平
行四边形是矩形.
【解析】
【分析】(1)按照步骤操作即可;
(2)根据矩形的判定定理推导,填空即可.
【小问 1 详解】
解:补全图形如下:
第6页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【小问 2 详解】
证明:∵ AD = BC = b, AB = DC = a,
∴四边形 ABCD是平行四边形(两组对边分别相等的四边形是平行四边形).
∵直线m ⊥ l ,
∴ ABC = 90 ,
∴四边形 ABCD 是矩形(有一个内角是直角的平行四边形是矩形).
故答案是:两组对边分别相等的四边形是平行四边形;90;有一个内角是直角的平行四边形是矩形.
20. 【答案】化简为: a2 + a,结果值为:5
【分析】先根据分式的混合运算顺序和运算法则化简原式,再根据已知等式可得答案.
1 a 1
【详解】解: a
a a2
a2 1 a2
=
a a 1
(a + 1) (a 1) a2
=
a a 1
= a2 + a ,
a2 + a 5 = 0
a2 + a = 5
1 a 1
a = a
2 + a = 5.
2
a a
21. 【答案】m =1, x1 = 2 , x2 =1
2
【分析】先根据根的判别式的意义得到 = ( 3) 4(m+1) 0 ,解不等式,从而得到正整数 m 的值,代
入原方程,然后利用因式分解法解方程即可.
2
【详解】根据题意得Δ = ( 3) 4(m+1) 0
5
解得m
4
所以正整数 m 的值为 1
代入原方程得 x2 3x + 2 = 0
第7页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
即 (x 2)(x 1) = 0
∴ x1 = 2 , x2 =1
22. 【答案】(1)见解析 (2)OE = 37
【分析】(1)根据矩形的对角线相等可得 AC = BD,对边平行可得 AD∥BC ,再证明出四边形
ADEC 是平行四边形,根据平行四边形的对边相等可得 AC = DE ,从而得证;
(2)如图,过点 O 作OF ⊥ CD 于点 F,欲求OE ,只需在直角 OEF 中求得OF、FE 的值即可.结合
三角形中位线求得OF ,结合矩形、平行四边形的性质以及勾股定理求得OE 即可.
【小问 1 详解】
∵四边形 ABCD是矩形,
∴ AC = BD,AD∥BC ,
又∵ DE∥ AC ,
∴四边形 ADEC 是平行四边形,
∴ AC = DE ,
∴ BD = DE ;
【小问 2 详解】
如图,过点 O 作OF ⊥ BC 于点 F,
∵四边形 ABCD是矩形,
∴ AC BD,点 O 是 AC, BD 的中点, AD = BC = 4,
1 1
∴OC = AC,OB = BD,
2 2
∴OC =OB,
1
∴CF = BF = BC = 2,
2
∴ F 点是 BC 的中点,
∴OF 是△BCD 的中位线,
1
∴OF = CD =1,
2
又∵四边形 ADEC 是平行四边形,
∴CE = AD = 4, .
第8页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∴ EF = CF +CE = 2+ 4 = 6.
在Rt△OEF 中,由勾股定理可得:OE = OF 2 + EF 2 = 12 + 62 = 37 .
【点睛】本题考查了矩形的性质,平行四边形的判定与性质,熟记各性质并求出四边形 ADEC 是平行四
边形是解题的关键.
23. 【答案】(1)见解析 (2)88.5 分;94 分
(3)1900 份
【分析】(1)用 20 减去第一、二、四、五组的频数即可得到第三组( 70 x 80)的频数,进而可补全
频数分布直方图;
(2)根据中位数和众数的定义求解即可;
(3)用样本百分比估计总体数量即可.
【小问 1 详解】
第三组( 70 x 80)的频数为: 20 1 1 7 9 = 2 ,
补全图形如下:
【小问 2 详解】
∵20 个数据按大小顺序排列,最中间的两个数据是第 10 和 11 个,
∴A 小区参加有奖问答活动的 20 名居民成绩的数据的中位数在80 x 90 这一组内的第 6 和 7 个数据的
88+89
平均数,即 =88.5;
2
B 小区参加有奖问答活动的 20 名居民成绩中出现次数最多的是 94 分,出现 4 次,
故 B 小区参加有奖问答活动的 20 名居民成绩中众数是 94 分,
故答案为:88.5 分;94 分;
【小问 3 详解】
9 10
2000+ 200=1900(份)
20 20
答:估计这两个小区的居委会一共需要准备 1900 份小奖品
24. 【答案】(1)见解析;
(2)见解析
第9页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
【分析】(1)根据直径所对的圆周角是直角及菱形的性质得到点M 是 BD 的中点即可解答;
(2)根据菱形的性质及全等三角形的判定得到 DBE≌ DBF ,再根据全等三角形的性质得到
BFD = DEB = 90 ,最后利用四边形的内角和及切线的判定即可解答.
【小问 1 详解】
解:连接 AM ,
∵ AD 为 O 的直径,
∴ AMD = 90 ,
∴ AM ⊥ BD ,
∵四边形 ABCD是菱形,
∴ AD = AB ,
∴点M 是 BD的中点,
∴ DM = BM ;
【小问 2 详解】
解:连接 DE ,
∵四边形 ABCD是菱形,
∴ DBE = DBF , DAB + ABC =180 ,
∴在 DBE 和 DBF ,
BE = BF
DBE = DBF ,
BD = BD
∴ DBE≌ DBF (SAS ),
∴ DEB = DFB ,
∵ AD 是 O 的直径,
∴ AED = DEB = 90 ,
∴ BFD = DEB = 90 ,
第10页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∵ DAB + ABC =180 ,
∴在四边形 ABFD 中, ADF + DFB =180 ,
∴ ADF = 90 ,
∴ AD ⊥ DF ,
∴ DF 是 O 的切线.
25. 【答案】(1)1, 2
5
(2)①1;② 2 xP
2
【分析】(1)先根据直线的解析式可求 a 的值,从而可得点 A 的坐标,再将点 A 坐标代入反比例函数的
解析式可得 k 的值;
(2)①先求出点 P 坐标,再根据反比例函数的解析式求出点 B 、C 坐标,然后结合函数图像、整点的定
义即可得;②由图可知点 P 不可能在点 A 下方,故点 P 在点 A 上方,结合函数图像列出不等式组求解即
可.
【小问 1 详解】
k
解: 函数 y = (x 0)的图像与一次函数 y = 2x 的图像交于点 A(a, 2),
x
2 = 2 a ,即 a =1,
A(1, 2),
( k
k
将 A 1, 2)代入反比例函数 y = (x 0)中, 2 = 解得: k = 2,
x 1
故答案为: a =1, k = 2;
【小问 2 详解】
2
①由(1)可知反比例函数解析式为 y = (x 0),
x
点 P 是射线OA上一点, P 的横坐标是 2 ,
y = 2 2 = 4
P (2,4)
2
将 x = 2 代入 y = (x 0),得 y =1
x
2 1
将 y = 4 代入 y = (x 0),得 x =
x 2
k
点 P 与 x轴, y 轴的垂线交函数 y = (x 0)的图像于点 B ,C ,
x
1
B (2,1),C ,4 ,
2
如图:
第11页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
结合函数图像可知,区域W 内有1个整数点;
②区域W 内恰有5个整点,由图可知点 P 只能位于A 的上方如图:
y 5
如图,当 P 的纵坐标为5时,横坐标为 x = = ,
2 2
5
结合图像可知,当 2 xP 时,区域内有5个整数点.
2
26. 【答案】(1) y1 y2 ,理由见解析
(2)m 2
【解析】
【分析】(1)当m = 2时,3 x2 5 ,将抛物线解析式化为顶点式,得到对称轴,根据 x x1, 2 的大小
判断与对称轴的距离,结合 a<0,即可得出答案;
第12页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
(2)根据题意可知满足 y1 = y2 ,即x 与x1 2关于对称轴 x =1对称,当 1 x1 2时,则x 2的最小值要
比 x1 = 2 时的对称点 0 小,x 2的最大值要比 x1 = 1时的对称点 3 大,解不等式组即可.
【小问 1 详解】
y1 y2 ;
2
理由:∵ y = ax2 2ax +8 = a (x 1) +8 a,
∴抛物线的对称轴是直线 x =1
当m = 2时,3 x2 5
∵ 1 x1 2,3 x2 5 ,对称轴是直线 x =1
∴x 比x 离对称轴近 1 2
∵ a<0,抛物线开口向下
∴ y1 y2
【小问 2 详解】
∵1 m x2 m + 7
∴1 m m + 7
解得m 3①
∵存在 x1, x2 ,满足 y1 = y2 ,且 1 x1 2
∴1 m 3
解得m 2②
综上,m 的取值范围是m 2
27. (1)
①依题意补全图形如图所示:
证明:∵AC绕点逆时针旋转 180°-α得到线段 CE
∴ AC = CE ,
∵点 F 是 DE的中点,
∴ DF = EF ,
∵点 C 与点 G 关于点 F 对称,
∴CF =GF ,
又∵ DFG = EFC ,
∴ DFG EFC ,
∴ DG = CE ,
∴ AC = DG ;
第13页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
②证明:∵边 AB 绕点 B顺时针旋转α(<0°α<180°)得到线段 BD,
∴ BD = BA,
设 ACB = x, ABC = y,则 BAC =180 (x + y) .
∴在四边形 BDEC 中,
BDE + CED = 360 DBC BCE =180 (x + y)
∵ DFG EFC ,
∴ GDF = CEF ;
∴ BDG = BDE + GDF =180 (x + y)
∴ BDG = BAC ;
∴ BDG BAC ,
∴ DGB = ACB ;
3
(2) FH = BC
4
28. 【答案】(1)2 2 ,3
(2)b 的取值范围是 3 b 6 或 6 b 3 ;
3 7
(3)2 t +1
2 2
【分析】(1)设经过点 M 的直线与 O 交于 E、F 两点,过点 O 作OH ⊥ EF 于 H,连接OM,OE ,利
用垂径定理得到 EF = 2EH ,由勾股定理可得当OH 最大时, EH 最小,即此时 EF 最小,求出
OM = 2 ,再由OH OM ,得到当点 H 与点 M 重合时,OH 有最大值 2 ,即可求出 EF 的最小值为
2 2 ,则被圆 O 截得的弦长取值范围为 2 2 x 4 ,再由被圆 O 截得的弦长为 3 的弦有 2 条,被圆 O
截得的弦长为 4 的弦只有 1 条,可得点 M 关于圆 O 的特征值为 3;
(2)根据题意得,关于圆 O的特征值为 4 的所有点都在以 O为圆心, 3 为半径的圆周上,分当b 0时和
当b 0时,两种情况讨论即可求解;
(3)由于同一平面内,对于任意一点 Q,经过 O、Q 的直线与圆 O 截得的弦(直径)都为 4,则点 Q 关
r =1 r = 2
于圆 O 的特征值不可能为 0,由此可得 rs 0,则 或 ;经过点 S 且弦长为 4(最长弦)的直
s = 2 s =1
第14页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
7
线有 1 条,弦长为 3(最短弦)的直线有 1 条,由(2)可知点 S 一定在以 O 为圆心,以 为半径的圆
2
3
上,同理点 R 一定在以 T 为圆心,以 为半径的圆上,则当满足以 O 为圆心,2 为半径的圆与以 T 为圆
2
3 7
心, 为半径的圆有交点,且同时满足以 O 为圆心, 为半径的圆与以 T 为圆心,1 为半径的圆有交
2 2
点时 t 的值符合题意,由此求解即可.
【小问 1 详解】
解:设经过点 M 的直线与 O 交于 E、F 两点,过点 O 作OH ⊥ EF 于 H,连接OM,OE ,
∴ EF = 2EH ,
在Rt△OEH 中,由勾股定理得EH = OE 2 OH 2 = 4 OH 2 ,
∴当OH 最大时, EH 最小,即此时 EF 最小,
∵点 M 的坐标为 (1,1),
∴OM = 12 +12 = 2 ,
又∵OH OM ,
∴当点 H 与点 M 重合时,OH 有最大值 2 ,
2
∴此时 EH 有最小值 4 ( 2 ) = 2 ,
∴ EF 的最小值为 2 2
∵过点 M 的直线被圆 O 截得的弦长的最大值为 4(直径),
∴被圆 O 截得的弦长取值范围为 2 2 x 4 ,
∴被圆 O 截得的弦长为正整数的只有是 3 或 4,
∵被圆 O 截得的弦长为 3 的弦有 2 条,被圆 O 截得的弦长为 4 的弦只有 1 条,
∴点 M 关于圆 O 的特征值为 3,
故答案为: 2 2 ,3;
【小问 2 详解】
第15页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
解:设点 G 是圆 O 的特征值为 4 的点,
由(1)可知经过一点 G 且弦长为 4(最长弦)的直线有 1 条,弦长为 3 的直线有 2 条,
∵特征值要保证为 4,
∴经过点 G 且弦长为 2 的直线有且只有 1 条,
∴经过点 G 的直线被圆 O 截得的弦长的最小值为 2,
∵ 22 12 = 3 ,
∴由(1)可知,关于圆 O 的特征值为 4 的所有点都在以 O 为圆心, 3 为半径的圆周上,
∵直线 y = x + b分别与 x,y 轴交于点 A,B,
∴ A( b,0), B (0,b),
∴OA =OB = b,
∴ OBH = 45
当b 0时,
∵线段 AB 上总存在关于圆 O 的特征值为 4 的点,
∴线段 AB 与以 O 为圆心, 3 为半径的圆有交点,
当线段 AB 与以 O 为圆心, 3 为半径的圆相切时,将切点设为 H,连接 OH,则OH = 3 ,
∴OB = 2OH = 6 ,
∴b1 = 6 ,
将以 O 为圆心, 3 为半径的圆与 y 轴正半轴的交点记为 B1,则OB1 = 3 ,
当线段 AB 与以 O 为圆心, 3 为半径的圆相交,且过点 B1时,可得b = 3 , 2
∴ 3 b 6 ;
同理可求当b 0时, 6 b 3 ;
综上,b 的取值范围是 3 b 6 或 6 b 3 ;
【小问 3 详解】
:∵同一平面内,对于任意一点 Q,经过 O、Q 的直线与圆 O 截得的弦(直径)都为 4,
∴点 Q 关于圆 O 的特征值不可能为 0,
第16页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
∴ rs 0,
∵ r + s = 3,且 r、s 都是整数,
r =1 r = 2
∴ 或 ;
s = 2 s =1
r =1
当 时,
s = 2
∴经过点 S 且弦长为 4(最长弦)的直线有 1 条,弦长为 3(最短弦)的直线有 1 条,
2
3 7
∴由(2)可知点 S 一定在以 O 为圆心,以 22 = 为半径的圆上,
2 2
r = 2 2 1 3
同理当 时,点 R 一定在以 T 为圆心,以 12 = 为半径的圆上,
s =1 2 2
3
∴当满足以 O 为圆心,2 为半径的圆与以 T 为圆心, 为半径的圆有交点,且同时满足以 O 为圆心,
2
7
为半径的圆与以 T 为圆心,1 为半径的圆有交点时 t 的值符合题意;
2
如图 3-1 所示,
3 7
当以 O 为圆心, 为半径的圆与以 T 为圆心,1 为半径的圆外切时,此时 t1 = +1;
2 2
3 3
如图 3-2 所示,当以 O 为圆心,2 为半径的圆与以 T 为圆心, 为半径的圆外切时,此时 t2 = 2 ;
2 2
3 7
综上所述,当2 t +1时,存在点 R,S,使得 r + s = 3.
2 2
第17页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
第18页/共18页
{#{QQABAQAAggggAJJ AAQgCAwHQCAIQkAAACSgGBFAAoAIBwRNABAA=}#}
同课章节目录
