21.1 二次函数 课件(共50张PPT)
文档属性
| 名称 | 21.1 二次函数 课件(共50张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 21:08:01 | ||
图片预览











文档简介
(共50张PPT)
九年级沪科版数学上册 第二十一章二次函数与反比例函数
21.1 二次函数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
情景导入
雨后天空的彩虹,公园里的喷泉,投篮等都会形成一条曲线.这些曲线能否用函数关系式表示?
1. 一次函数的一般形式是_________________.
y=kx+b (k≠0)
2. 一元二次方程的一般形式是______________________,
为什么a≠0?____________________________________
ax2+bx+c=0 (a≠0)
当a=0时,方程不是一元二次方程.
某正方形边长为x,面积为S,则其面积S与边长x之间的函数关系式是什么?它是一次函数吗?为什么?
函数关系是S=x2,不是一次函数,因为右边不是x的一次式.
旧知回顾
导入新课
●一次函数:
●正比例函数:
一条直线
●反比例函数:y= (k≠0)
(我们后面学)
双曲线
思考:
●什么是二次函数?
●二次函数的图象是什么样的?
y=kx+b (k≠0)
y=kx (k≠0)
函数
观察下面图片,说说这些是什么样的曲线?
喷泉形成的轨迹
拱桥
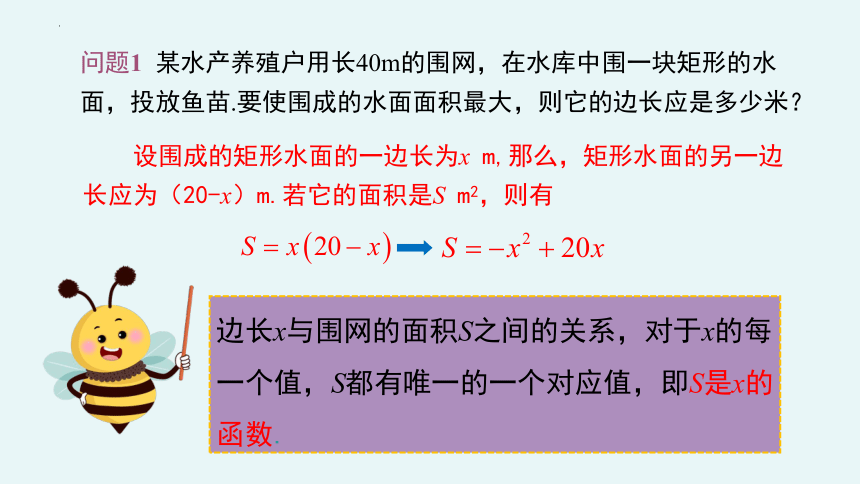
问题1 某水产养殖户用长40m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?
设围成的矩形水面的一边长为x m,那么,矩形水面的另一边长应为(20-x)m.若它的面积是S m2,则有
边长x与围网的面积S之间的关系,对于x的每一个值,S都有唯一的一个对应值,即S是x的函数.
问题2 有一玩具厂,如果安排装配工15人,那么每人每天可装配玩具190个;如果增加人数,那么每增加1人,可使每人每天少装配玩具10个.问增加多少人才能使每天装配玩具总数最多?最多为多少?
设增加 x 人,这时,则共有 个装配工,每人每天可少装配10x 个玩具,因此,每人每天只装配 个玩具.所以,增加人数后,每天装配玩具总数y可表示为y=________________.
(15+x)
(190-10x)
整理为:
y=-10x2+40x+2850
(190-10x)(15+x)
每天装配玩具总数y与增加x人之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
根据上述探究,回答以下问题:
(1) 问题①中,矩形面积S与其一边长x之间的函数关系式为S=-x2+20x (0<x<20),它是一次函数吗?为什么?
(2) 问题②中,增加x人后,每天装配玩具总数y可表示为
y=-10x2+40x+2850.它是一次函数吗?为什么?
它不是一次函数;右边不是x的一次式.
它不是一次函数;右边不是x的一次式.
上面两个函数解析式具有哪些共同特征?
新知探究
一般地,表达式形如 y=ax2+bx+c
(a、b、c是常数,且a≠0)的函数叫做x的二次函数.其中x是自变量,a为二次项系数,b为一次项系数,c为常数项.
概念归纳
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
概念归纳
1.下列函数中是二次函数的有 。
二次函数:y=ax +bx+c
(a,b,c为常数,a≠0)
√
a=0
×
最高次数是4
×
×
√
=x2
√
①⑤⑥
练一练
2.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
3.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
B
练一练
4.分别指出下面三个函数解析式中各项的系数.
二次项系数 一次项系数 常数项
y=3x2(x>0)
d=n2-n(n≥3)
y=2x2+4x+10
3
0
0
0
2
4
10
练一练
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
总结归纳
二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0.
想一想
列出下列函数的关系式.
(1)一个圆柱的高等于底面半径的2倍,则它的表面积 S 与底面半径 r 之间的关系式为_________.
(2)某工厂一种产品现在年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加 x 倍,那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定,y 与 x 之间的关系应怎样表示?______________.
S=6πr2
y=20(1+x)2
在实际问题中列二次函数的解析式
新知探究
(3) n 支球队参加比赛,每
两队之间进行一场比赛,
则比赛的场次数 m 与球队
数 n 之间的关系式为
_____________.
一直角三角形两直角边之和为 20,其中一条直角边长为 x,写出它的面积 S 与直角边长 x 之间的函数解析式,并写出自变量 x 的取值范围.
解:根据题意,得
自变量 x 的取值范围是0<x<20.
练一练
二次函数定义的应用
例1.
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
注意: 第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
新知探究
1.已知: ,k取什么值时,y是x的二次函数?
解:当 =2且k+2≠0,即k=-2时, y是x的二次函数.
解:
由题意得:
∴m≠±3
练一练
解:
由题意得:
【解题归纳】本题考查正比例函数和二次函数的概念,这类题需紧扣概念的特征进行解题.
练一练
例2:某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
典例剖析
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得 -10x2+180x+400=1120,
整理得 x2-18x+72=0,
解得 x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【解题归纳】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
思考:
1.已知二次函数y=-10x2+180x+400 ,自变量x的取值范围是什么?
2.在例3中,所得出y关于x的函数关系式y=-10x2+180x+400,其自变量x的取值范围与1中相同吗?
【总结】二次函数自变量的取值范围一般是全体实数,但是在实际问题中,自变量的取值范围应使实际问题有意义.
例3. 一个二次函数 .
(1)求k的值.
(2)当x=0.5时,y的值是多少?
解:
(1)由题意,得
解得
将x=0.5代入函数关系式 .
(2)当k=2时,
求二次函数的值
新知探究
此类型题考查二次函数的概念,要抓住二次项系数不为0及自变量指数为2这两个关键条件,求出字母参数的值,得到函数解析式,再用代入法将x的值代入其中,求出y的值.
总结归纳
1.若函数 是二次函数,求:
(1)求a的值.
(2) 求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为 .
(3)将x=-2代入函数关系式中,有
练一练
2.某商店经销一种销售成本为每千克40元的商品,根据市场分析,若按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量 就减少10kg,针对这种商品的销售情况,请解答下列问题:
(1)当销售单价为每千克55元时,计算月销售量和销售利润分别为多少?
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出自变量x的取值范围)
练一练
3.矩形的周长为16cm,它的一边长为x(cm),面积为y(cm2).求
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x (0<x<8);
(2)当x=3时,y=-32+8×3=15 cm2 .
练一练
1.设圆的半径为 r,请填空:
(1)这个圆的周长 C = ,它是 r 的 函数;
(2)这个圆的面积 S= ,它是 r 的 函数.
课本练习
2.在下列表达式中,哪些是二次函数?
(1)正常情况下,一个人在运动时每分所能承受的最高心跳次数b与这个人的年龄a之间的关系可表示为
b = 0.8(220-a);
(2)圆锥的高为 h,它的体积V与底面半径r之间的关系可表示为
(h为定值);
2πr
一次
πr
二次
(3)物体自由下落时,下落高度h与下落时间t之间的关系可表示为
(g为定值);
(4)导线的电阻为R,当导线中有电流通过时,电功率P与电流1之间的关系可表示为
(R 为定值).
【解析】(2)(3)(4)是二次函数.
解:y=3x2-1,y=5x2-2x,y=-2x2+x-1,
y=(x-2)(2x+1)是二次函数.
1. 在下列表达式中,x为自变量,问哪些是二次
函数?
y=3x2-1,y=5x2-2x,y=-2x2+x-1,
y=4-x3, , ,y=(x-2)(2x+1).
习题21.1
2.正方形的边长为5,如果边长增加x,那么面积
增加y,求y与x之间的函数表达式.
解:y=x2+10x(x≥0)
解:S=2x2+32x(x>0).
3.长方体的长与宽均为x,高为8,求长方体表面积S与x之间的函数表达式.
从已知半径为R的圆板上挖掉一个半径为r
(r<R)的同心圆版,求所剩圆环面积S与r之间的函数表达式.
4.
解:S=πR2-πr2(0<r<R) .
在一块一边长为35 m、另一边长为20 m的矩形空地上修建花坛,如果在四周留出宽度为x m的小路,中间花坛面积为y m2,求y与x之间的函数表达式.
5.
解:y=4x2-110x+700(0<x<10).
某商场今年一月份销售额为50万元,二、三月份平均每月销售增长率为x,求三月份销售额y与x之间的函数表达式.
6.
解:y=50x2+100x+50.
ax2+bx+c
自变量
D
分层练习-基础
B
A
y=-x2-x+2
-1
-1
2
分层练习-基础
实
有意义
C
B
分层练习-基础
分层练习-基础
D
B
分层练习-巩固
-5
2
a(1+x)2
二次
分层练习-巩固
y=-2x2+30x
5≤x<15
分层练习-巩固
分层练习-拓展
A
课堂反馈
课堂反馈
二次函数
定 义
y=ax2+bx+c(a ≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
课堂小结
九年级沪科版数学上册 第二十一章二次函数与反比例函数
21.1 二次函数
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.理解掌握二次函数的概念和一般形式.(重点)
2.会利用二次函数的概念解决问题.
3.会列二次函数表达式解决实际问题.(难点)
情景导入
雨后天空的彩虹,公园里的喷泉,投篮等都会形成一条曲线.这些曲线能否用函数关系式表示?
1. 一次函数的一般形式是_________________.
y=kx+b (k≠0)
2. 一元二次方程的一般形式是______________________,
为什么a≠0?____________________________________
ax2+bx+c=0 (a≠0)
当a=0时,方程不是一元二次方程.
某正方形边长为x,面积为S,则其面积S与边长x之间的函数关系式是什么?它是一次函数吗?为什么?
函数关系是S=x2,不是一次函数,因为右边不是x的一次式.
旧知回顾
导入新课
●一次函数:
●正比例函数:
一条直线
●反比例函数:y= (k≠0)
(我们后面学)
双曲线
思考:
●什么是二次函数?
●二次函数的图象是什么样的?
y=kx+b (k≠0)
y=kx (k≠0)
函数
观察下面图片,说说这些是什么样的曲线?
喷泉形成的轨迹
拱桥
问题1 某水产养殖户用长40m的围网,在水库中围一块矩形的水面,投放鱼苗.要使围成的水面面积最大,则它的边长应是多少米?
设围成的矩形水面的一边长为x m,那么,矩形水面的另一边长应为(20-x)m.若它的面积是S m2,则有
边长x与围网的面积S之间的关系,对于x的每一个值,S都有唯一的一个对应值,即S是x的函数.
问题2 有一玩具厂,如果安排装配工15人,那么每人每天可装配玩具190个;如果增加人数,那么每增加1人,可使每人每天少装配玩具10个.问增加多少人才能使每天装配玩具总数最多?最多为多少?
设增加 x 人,这时,则共有 个装配工,每人每天可少装配10x 个玩具,因此,每人每天只装配 个玩具.所以,增加人数后,每天装配玩具总数y可表示为y=________________.
(15+x)
(190-10x)
整理为:
y=-10x2+40x+2850
(190-10x)(15+x)
每天装配玩具总数y与增加x人之间的关系,对于x的每一个值,y都有唯一的一个对应值,即y是x的函数.
根据上述探究,回答以下问题:
(1) 问题①中,矩形面积S与其一边长x之间的函数关系式为S=-x2+20x (0<x<20),它是一次函数吗?为什么?
(2) 问题②中,增加x人后,每天装配玩具总数y可表示为
y=-10x2+40x+2850.它是一次函数吗?为什么?
它不是一次函数;右边不是x的一次式.
它不是一次函数;右边不是x的一次式.
上面两个函数解析式具有哪些共同特征?
新知探究
一般地,表达式形如 y=ax2+bx+c
(a、b、c是常数,且a≠0)的函数叫做x的二次函数.其中x是自变量,a为二次项系数,b为一次项系数,c为常数项.
概念归纳
温馨提示:
(1)等号左边是变量y,右边是关于自变量x的整式;
(2)a,b,c为常数,且a≠ 0;
(3)等式的右边最高次数为 2,可以没有一次项和常数项,但不能没有二次项.
概念归纳
1.下列函数中是二次函数的有 。
二次函数:y=ax +bx+c
(a,b,c为常数,a≠0)
√
a=0
×
最高次数是4
×
×
√
=x2
√
①⑤⑥
练一练
2.下列函数关系式中,一定为二次函数的是( )
A.y=3x-1 B.y=ax2+bx+c
C.s=2t2-2t+1 D.y=x2+
3.下列各式中,y是x的二次函数的是( )
A.y=ax2+bx+c B.x2+y-2=0
C.y2-ax=2 D.x2-y2+1=0
C
B
练一练
4.分别指出下面三个函数解析式中各项的系数.
二次项系数 一次项系数 常数项
y=3x2(x>0)
d=n2-n(n≥3)
y=2x2+4x+10
3
0
0
0
2
4
10
练一练
判断一个函数是不是二次函数,先看原函数和整理化简后的形式再作判断.除此之外,二次函数除有一般形式y=ax2+bx+c(a≠0)外,还有其特殊形式如y=ax2,y=ax2+bx, y=ax2+c等.
总结归纳
二次函数的一般式y=ax2+bx+c(a≠0)与一元二次方程ax2+bx+c=0(a≠0)有什么联系和区别?
联系:(1)等式一边都是ax2+bx+c且a ≠0;
(2)方程ax2+bx+c=0可以看成是函数y= ax2+bx+c中y=0时得到的.
区别:前者是函数.后者是方程.等式另一边前者是y,后者是0.
想一想
列出下列函数的关系式.
(1)一个圆柱的高等于底面半径的2倍,则它的表面积 S 与底面半径 r 之间的关系式为_________.
(2)某工厂一种产品现在年产量是20件,计划今后两年增加产量,如果每年都比上一年的产量增加 x 倍,那么两年后这种产品的产量 y 将随计划所定的 x 的值而确定,y 与 x 之间的关系应怎样表示?______________.
S=6πr2
y=20(1+x)2
在实际问题中列二次函数的解析式
新知探究
(3) n 支球队参加比赛,每
两队之间进行一场比赛,
则比赛的场次数 m 与球队
数 n 之间的关系式为
_____________.
一直角三角形两直角边之和为 20,其中一条直角边长为 x,写出它的面积 S 与直角边长 x 之间的函数解析式,并写出自变量 x 的取值范围.
解:根据题意,得
自变量 x 的取值范围是0<x<20.
练一练
二次函数定义的应用
例1.
(1)m取什么值时,此函数是正比例函数?
(2) m取什么值时,此函数是二次函数?
解:
(1)由题可知,
解得
(2)由题可知,
解得
m=3.
注意: 第(2)问易忽略二次项系数a≠0这一限制条件,从而得出m=3或-3的错误答案,需要引起同学们的重视.
新知探究
1.已知: ,k取什么值时,y是x的二次函数?
解:当 =2且k+2≠0,即k=-2时, y是x的二次函数.
解:
由题意得:
∴m≠±3
练一练
解:
由题意得:
【解题归纳】本题考查正比例函数和二次函数的概念,这类题需紧扣概念的特征进行解题.
练一练
例2:某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
解:∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天产量减少5件,
∴第x档次,提高了(x-1)档,利润增加了2(x-1)元.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
典例剖析
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.
解:由题意可得 -10x2+180x+400=1120,
整理得 x2-18x+72=0,
解得 x1=6,x2=12(舍去).
所以,该产品的质量档次为第6档.
【解题归纳】解决此类问题的关键是要吃透题意,确定变量,建立函数模型.
思考:
1.已知二次函数y=-10x2+180x+400 ,自变量x的取值范围是什么?
2.在例3中,所得出y关于x的函数关系式y=-10x2+180x+400,其自变量x的取值范围与1中相同吗?
【总结】二次函数自变量的取值范围一般是全体实数,但是在实际问题中,自变量的取值范围应使实际问题有意义.
例3. 一个二次函数 .
(1)求k的值.
(2)当x=0.5时,y的值是多少?
解:
(1)由题意,得
解得
将x=0.5代入函数关系式 .
(2)当k=2时,
求二次函数的值
新知探究
此类型题考查二次函数的概念,要抓住二次项系数不为0及自变量指数为2这两个关键条件,求出字母参数的值,得到函数解析式,再用代入法将x的值代入其中,求出y的值.
总结归纳
1.若函数 是二次函数,求:
(1)求a的值.
(2) 求函数关系式.
(3)当x=-2时,y的值是多少?
解:
(1)由题意,得
解得
(2)当a=-1时,函数关系式为 .
(3)将x=-2代入函数关系式中,有
练一练
2.某商店经销一种销售成本为每千克40元的商品,根据市场分析,若按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量 就减少10kg,针对这种商品的销售情况,请解答下列问题:
(1)当销售单价为每千克55元时,计算月销售量和销售利润分别为多少?
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式(不必写出自变量x的取值范围)
练一练
3.矩形的周长为16cm,它的一边长为x(cm),面积为y(cm2).求
(1)y与x之间的函数解析式及自变量x的取值范围;
(2)当x=3时矩形的面积.
解:(1)y=(8-x)x=-x2+8x (0<x<8);
(2)当x=3时,y=-32+8×3=15 cm2 .
练一练
1.设圆的半径为 r,请填空:
(1)这个圆的周长 C = ,它是 r 的 函数;
(2)这个圆的面积 S= ,它是 r 的 函数.
课本练习
2.在下列表达式中,哪些是二次函数?
(1)正常情况下,一个人在运动时每分所能承受的最高心跳次数b与这个人的年龄a之间的关系可表示为
b = 0.8(220-a);
(2)圆锥的高为 h,它的体积V与底面半径r之间的关系可表示为
(h为定值);
2πr
一次
πr
二次
(3)物体自由下落时,下落高度h与下落时间t之间的关系可表示为
(g为定值);
(4)导线的电阻为R,当导线中有电流通过时,电功率P与电流1之间的关系可表示为
(R 为定值).
【解析】(2)(3)(4)是二次函数.
解:y=3x2-1,y=5x2-2x,y=-2x2+x-1,
y=(x-2)(2x+1)是二次函数.
1. 在下列表达式中,x为自变量,问哪些是二次
函数?
y=3x2-1,y=5x2-2x,y=-2x2+x-1,
y=4-x3, , ,y=(x-2)(2x+1).
习题21.1
2.正方形的边长为5,如果边长增加x,那么面积
增加y,求y与x之间的函数表达式.
解:y=x2+10x(x≥0)
解:S=2x2+32x(x>0).
3.长方体的长与宽均为x,高为8,求长方体表面积S与x之间的函数表达式.
从已知半径为R的圆板上挖掉一个半径为r
(r<R)的同心圆版,求所剩圆环面积S与r之间的函数表达式.
4.
解:S=πR2-πr2(0<r<R) .
在一块一边长为35 m、另一边长为20 m的矩形空地上修建花坛,如果在四周留出宽度为x m的小路,中间花坛面积为y m2,求y与x之间的函数表达式.
5.
解:y=4x2-110x+700(0<x<10).
某商场今年一月份销售额为50万元,二、三月份平均每月销售增长率为x,求三月份销售额y与x之间的函数表达式.
6.
解:y=50x2+100x+50.
ax2+bx+c
自变量
D
分层练习-基础
B
A
y=-x2-x+2
-1
-1
2
分层练习-基础
实
有意义
C
B
分层练习-基础
分层练习-基础
D
B
分层练习-巩固
-5
2
a(1+x)2
二次
分层练习-巩固
y=-2x2+30x
5≤x<15
分层练习-巩固
分层练习-拓展
A
课堂反馈
课堂反馈
二次函数
定 义
y=ax2+bx+c(a ≠0,a,b,c是常数)
一般形式
右边是整式;
自变量的指数是2;
二次项系数a ≠0.
特殊形式
y=ax2;
y=ax2+bx;
y=ax2+c(a ≠0,a,b,c是常数).
课堂小结
