20.1.2.1中位数和众数(同步课件)-2023-2024学年八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 20.1.2.1中位数和众数(同步课件)-2023-2024学年八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览











文档简介
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.1.2.1
中位数和众数
情景引入
交流讨论,各抒己见,
阅读教材相关内容,
归纳出中位数的概念和确定方法.
在一次数学测试中,全班数学平均成绩是78分,小明考了83分,小明说自己的成绩在班里是中上水平,你认为小明的说法合适吗?
思考
任务
中位数
新知探究
将一组数据按照由小到大(或由大到小)的顺序排列:
如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;
如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
如图, 图(1)中5个数据的中位数x3 ;
图(2)中6个数据的中位数为
12????3+????4
?
????1
?
中位数
????2
?
????3
?
????4
?
????5
?
(1)
中位数
????1
?
????2
?
????3
?
????4
?
????5
?
????6
?
(2)
特别注意
新知探究
求中位数的步骤
首先将数据按照由小到大(或由大到小)的顺序排列;
然后数清数据个数是奇数还是偶数,如果数据个数为奇数,则取中间的数作为中位数,如果数据的个数为偶数,则取中间位置两数的平均值作为中位数.
一组数据的中位数是唯一的,中位数的优势在于受极端值的影响较小,故当一组数据中的个别数据的变化较大时,可用中位数描述其平均水平,中位数的缺点在于不能充分利用各数据的信息.
典例精析
例1
下面两组数据的中位数是多少?
(1)5,6,2,3,2
(2)5,6,2,4,3,5
提示:确定中位数要先排序、看奇偶,再计算.
解:(1) 中位数是3;
(2)中位数是4.5.
典例精析
例2
一组数据18,22,15,13,x,7,它的中位数是16,则x的值是_______.
17
解: 这组数据有6个,中位数是中间两个数的平均数.因为7<13<15<16<18<22,所以中间两个数必须是15,x,故(15+x)÷2=16,即x=17.
典例精析
例3
某班四个小组的人数如下:10,10,x,8,已知这组数据的中位数与平均数相等,求这组数据的中位数.
解:
情况一: 时,
情况二:当8情况三:当 时
综上,这组数据的中位数是9或10.
归纳总结
典例精析
2.如果一组数据中有极端数据,中位数能比平均数更合理地反映该组数据的整体水平.
1.中位数是一个位置代表值(中间数),它是唯一的.
3.如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半,反映一组数据的中间水平.
中位数的特征及意义:
新知探究
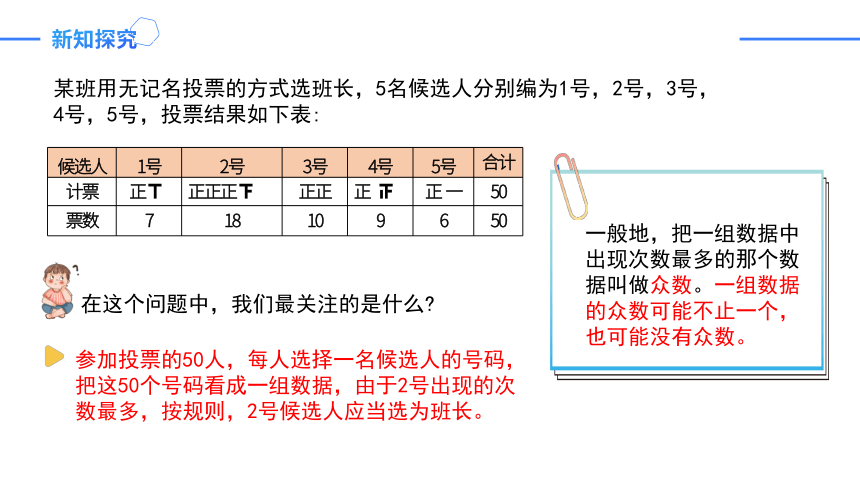
在这个问题中,我们最关注的是什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}候选人
1号
2号
3号
4号
5号
合计
计票
正
正正正
正正
正
正 一
50
票数
7
18
10
9
6
50
某班用无记名投票的方式选班长,5名候选人分别编为1号,2号,3号,4号,5号,投票结果如下表:
参加投票的50人,每人选择一名候选人的号码,把这50个号码看成一组数据,由于2号出现的次数最多,按规则,2号候选人应当选为班长。
一般地,把一组数据中出现次数最多的那个数据叫做众数。一组数据的众数可能不止一个,也可能没有众数。
总结
新知探究
注意:
(1)一组数据的众数一定出现在这组数据中.
(2)一组数据的众数可能不止一个.如1,1,2,3,3,5中众数是1和3.
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如1,1,1,2,2,5中众数是1而不是3.
一组数据中出现次数最多的数据称为这组数据的众数.
新知探究
某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150.
(1)求这15个销售员该月销量的平均数、中位数和众数;
解:将数据排序之后为:
120、120、150、150、150、210、210、210、210、210、250、250、250、510、1800.
故平均数为320件
中位数为210件
众数为210件
新知探究
(2)假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由。
解:(2)不合理。因为15人中有13人的销售额达不到320件(320虽是原始数据的平均数,却不能反映营销人员的一般水平),销售额定为210件合适,因为它既是中位数又是众数,是大部分人能达到的定额.
求众数时只要看在一组数中重复出现次数最多的数据就是众数.如果有两个或两个以上数据重复出现的次数都最多,那么这几个数据都是这组数据的众数.当一组数据中有不少数据多次重复出现时,我们往往关心众数.通常的“最佳”、“最受欢迎”、“最畅销”等等的评选活动都是用投票的方法取众数得到的.
新知探究
(1)一组数据的中位数只有一个.
(2)一组数据的中位数一定是这组数据中的某个数据.
(3)一组数据的众数只有一个.
(4)一组数据的众数一定是这组数据中的某个数 .
(5)一组数据的中位数、众数可以是同一个数据.
(6)中位数和众数没有单位.
√
×
√
√
×
判断正误,并说明理由.
×
典例精析
在10块面积都是100m2的田地上试种A,B两个品种的小麦,每个品种的小麦各试种5块,产量如下:
品种A:80,85,85,90,95
品种B:65,85,90,90,90
甲认为品种A比品种B的产量高,乙认为品种B比品种A的产量高.
(1)请你分析甲和乙判断的依据.
(2)根据试验数据,你认为该选择哪个品种推广种植?请说明理由.
解:(1)A的平均数为87,中位数为85,众数为85;B的平均数为84,中位数为90,众数为90.所以甲是以平均数作为判断的依据,乙可能是以中位数和众数作为依据的.
(2)使用A.因为B虽然众数和中位数都比A高,但是其有一个非常小的数值65,数据不具有很好的集中趋势,而相比与B,A则更集中且平均值更高.
例4
新知探究
解:(1) 45个数据的平均数为
( 5×2+10×6+15×14+20×12+25×8+30×3)÷45
= 18(min).
将这45 个数由小到大排列,第23个数据是20min,
所以中位数为20min.
所用时间出现最多的是15 min,所以众数是15 min.
统计全班45名学生每天回家路上所用的时间。如果时间取最接近5的倍数的整数,那么整理后的数据如下表:
求所用时间的平均数、中位数和众数。
所用时间/min
5
10
15
20
25
30
合计
人数/名
2
6
14
12
8
3
45
例5
归纳总结
典例精析
众数是当一组数据中某一数据重复出现较多时,人
们往往关心的一个量,众数不受极端值的影响,这是它
的一个优势,缺点是当众数有多个且众数的频数相对较
小时可靠性小,局限性大.
中位数仅与数据的排列位置有关,不易受极端值影
响,中位数可能出现在所给数据中,也可能不在所给的
数据中.当一组数据中的个别数据变动较大时,可用中
位数描述其趋势,中位数的计算很少.
典例精析
中等水平
多数水平
典例精析
例6
某班50名学生中,13岁6人,14岁的25人,15岁的16人,16岁的3人.那么,这个班同 学年龄的众数和中位数分别是( )
A、13,16 B、14,11 C、14,14 D、14,16
C
数据
13岁
14岁
15岁
16岁
出现次数
6人
25人
16人
3人
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
典例精析
例7
某公司的43名职工的月工资(以元为单位)如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}职员
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
30
工资
5500
5000
3500
3000
2500
2000
1500
(1)求该公司职员月工资的平均数、中位数、众数?(精确到元)
解:1953 、1500、1500;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
解:2872、1500、1500;
典例精析
例7
某公司的43名职工的月工资(以元为单位)如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}职员
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
30
工资
5500
5000
3500
3000
2500
2000
1500
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
解析:(3)中位数或众数均能反映该公司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平.
典例精析
例8
七年级(6)班三位同学最近的五次数学测验
成绩(单位:分)分别是:
他们都认为自己的数学成绩比其他两位同学好,他们比较的依据分别是什么?
解: 小华成绩的众数是_____,中位数是_____,平均数是_____;
小明成绩的众数是_____,中位数是_____,平均数是_____;
小丽成绩的众数是_____,中位数是_____,平均数是_____.
98
62
95
98
89.4
84.2
99
85
77
因为他们之中,小华的平均数最大,小明的中位数最大,
小丽的众数最大,所以都认为自己的成绩比其他两位同学好.
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
解:(1)样本数据的众数是_____,中位数是_____,平均数约是_____.
可以推测,这个电商营销部营业员的月销售额为_____万元的人数最多,
中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
20
20
大
三分之一
解:(2)这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
解:(3)月销售额可以定为每月____万元(中位数).因为从样本情况看,月销售额在____万元以上(含18万元)的有16人,占总人数的一半左右.可以估计,如果月销售额定为____万元,将有一半左右的营业员获得奖励.
18
18
18
典例精析
例10
下面是某校七年级(6)班两组女生的体重(单位:kg):
(1)分别求这两组数据的平均数、众数、中位数,并解释它们的实际意义(结果取整数);
(2)比较这两组数据的平均数、众数、中位数,谈谈你对它们的认识 .
解:(1)第1组数据的平均数是44,众数是42,中位数是40;
第2组数据的平均数约为40,众数是42,中位数是40.
(2)这两组数据中,只有一个数据不同,第1组是75,第2组是45,
因此这两组数据的平均数不同,但它们的中位数和众数相同.
由此可以看出,平均数受极值的影响较大,中位数和众数不受极值的影响.
第1组 35 36 38 40 42 42 75
第2组 35 36 38 40 42 42 45
归纳总结
中位数和众数
中位数:中间的一个数,或中间的两个数的平均数.
众数:出现次数最多的数.
平均数、中位数、众数的特征:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
当堂检测
课堂练习
1.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分
B.96分,96分
C.94分,96.4分
D.96分,96.4分
D
当堂检测
2.数据1,2, 8,5,3,9,5,4,5,4的众数、中位数分别为(???? )
A.4.5、5?? ??B.5、4.5?? ??C.5、4??? ??D.5、5?
3.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数?? B.中位数??? C.众数
B
B
4.已知一组数据:x1=4,x2=5,x3=6,x4=7,它们出现的次数依次为2,3,2,1,则这组数据的众数为 ,中位数为 ,平均数为 .
5
5
5.25
当堂检测
5.根据实际情况填写(填平均数、中位数、众数)
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注 .
③被招聘的员工关注公司员工工资的 .
中位数
平均数
众数
6.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:
甲群:13、13、14、15、15、15、16、17、17.
乙群:3、4、4、5、5、6、6、54、57.
(1)甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 .
(2)乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映乙群游客年龄特征的是 .
15
15
15
16
4、5、6
5
众数
众数
当堂检测
7.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人.年)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
根据表中提供的信息填空:
(1)该公司每人所创年利润的平均数是( )
万元,中位数是( )万元,众数是( )万元.
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
3.2
2.1
1.5和2.1
中位数
当堂检测
课堂练习
8.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时)
0
1
1.5
2
2.5
3
3.5
4
人数
2
2
6
12
13
4
3
(1)填写图表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
20.1.2.1
中位数和众数
情景引入
交流讨论,各抒己见,
阅读教材相关内容,
归纳出中位数的概念和确定方法.
在一次数学测试中,全班数学平均成绩是78分,小明考了83分,小明说自己的成绩在班里是中上水平,你认为小明的说法合适吗?
思考
任务
中位数
新知探究
将一组数据按照由小到大(或由大到小)的顺序排列:
如果数据的个数是奇数,则称处于中间位置的数为这组数据的中位数;
如果数据的个数是偶数,则称中间两个数据的平均数为这组数据的中位数.
如图, 图(1)中5个数据的中位数x3 ;
图(2)中6个数据的中位数为
12????3+????4
?
????1
?
中位数
????2
?
????3
?
????4
?
????5
?
(1)
中位数
????1
?
????2
?
????3
?
????4
?
????5
?
????6
?
(2)
特别注意
新知探究
求中位数的步骤
首先将数据按照由小到大(或由大到小)的顺序排列;
然后数清数据个数是奇数还是偶数,如果数据个数为奇数,则取中间的数作为中位数,如果数据的个数为偶数,则取中间位置两数的平均值作为中位数.
一组数据的中位数是唯一的,中位数的优势在于受极端值的影响较小,故当一组数据中的个别数据的变化较大时,可用中位数描述其平均水平,中位数的缺点在于不能充分利用各数据的信息.
典例精析
例1
下面两组数据的中位数是多少?
(1)5,6,2,3,2
(2)5,6,2,4,3,5
提示:确定中位数要先排序、看奇偶,再计算.
解:(1) 中位数是3;
(2)中位数是4.5.
典例精析
例2
一组数据18,22,15,13,x,7,它的中位数是16,则x的值是_______.
17
解: 这组数据有6个,中位数是中间两个数的平均数.因为7<13<15<16<18<22,所以中间两个数必须是15,x,故(15+x)÷2=16,即x=17.
典例精析
例3
某班四个小组的人数如下:10,10,x,8,已知这组数据的中位数与平均数相等,求这组数据的中位数.
解:
情况一: 时,
情况二:当8
综上,这组数据的中位数是9或10.
归纳总结
典例精析
2.如果一组数据中有极端数据,中位数能比平均数更合理地反映该组数据的整体水平.
1.中位数是一个位置代表值(中间数),它是唯一的.
3.如果已知一组数据的中位数,那么可以知道,小于或大于这个中位数的数据各占一半,反映一组数据的中间水平.
中位数的特征及意义:
新知探究
在这个问题中,我们最关注的是什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}候选人
1号
2号
3号
4号
5号
合计
计票
正
正正正
正正
正
正 一
50
票数
7
18
10
9
6
50
某班用无记名投票的方式选班长,5名候选人分别编为1号,2号,3号,4号,5号,投票结果如下表:
参加投票的50人,每人选择一名候选人的号码,把这50个号码看成一组数据,由于2号出现的次数最多,按规则,2号候选人应当选为班长。
一般地,把一组数据中出现次数最多的那个数据叫做众数。一组数据的众数可能不止一个,也可能没有众数。
总结
新知探究
注意:
(1)一组数据的众数一定出现在这组数据中.
(2)一组数据的众数可能不止一个.如1,1,2,3,3,5中众数是1和3.
(3)众数是一组数据中出现次数最多的数据而不是数据出现的次数,如1,1,1,2,2,5中众数是1而不是3.
一组数据中出现次数最多的数据称为这组数据的众数.
新知探究
某公司销售部有营销人员15人,销售部为了制定某种商品的销售金额,统计了这15个人的销售量如下(单位:件)1800、510、250、250、210、250、210、210、150、210、150、120、120、210、150.
(1)求这15个销售员该月销量的平均数、中位数和众数;
解:将数据排序之后为:
120、120、150、150、150、210、210、210、210、210、250、250、250、510、1800.
故平均数为320件
中位数为210件
众数为210件
新知探究
(2)假设销售部负责人把每位营销员的月销售定额定为320件,你认为合理吗?如果不合理,请你制定一个合理的销售定额并说明理由。
解:(2)不合理。因为15人中有13人的销售额达不到320件(320虽是原始数据的平均数,却不能反映营销人员的一般水平),销售额定为210件合适,因为它既是中位数又是众数,是大部分人能达到的定额.
求众数时只要看在一组数中重复出现次数最多的数据就是众数.如果有两个或两个以上数据重复出现的次数都最多,那么这几个数据都是这组数据的众数.当一组数据中有不少数据多次重复出现时,我们往往关心众数.通常的“最佳”、“最受欢迎”、“最畅销”等等的评选活动都是用投票的方法取众数得到的.
新知探究
(1)一组数据的中位数只有一个.
(2)一组数据的中位数一定是这组数据中的某个数据.
(3)一组数据的众数只有一个.
(4)一组数据的众数一定是这组数据中的某个数 .
(5)一组数据的中位数、众数可以是同一个数据.
(6)中位数和众数没有单位.
√
×
√
√
×
判断正误,并说明理由.
×
典例精析
在10块面积都是100m2的田地上试种A,B两个品种的小麦,每个品种的小麦各试种5块,产量如下:
品种A:80,85,85,90,95
品种B:65,85,90,90,90
甲认为品种A比品种B的产量高,乙认为品种B比品种A的产量高.
(1)请你分析甲和乙判断的依据.
(2)根据试验数据,你认为该选择哪个品种推广种植?请说明理由.
解:(1)A的平均数为87,中位数为85,众数为85;B的平均数为84,中位数为90,众数为90.所以甲是以平均数作为判断的依据,乙可能是以中位数和众数作为依据的.
(2)使用A.因为B虽然众数和中位数都比A高,但是其有一个非常小的数值65,数据不具有很好的集中趋势,而相比与B,A则更集中且平均值更高.
例4
新知探究
解:(1) 45个数据的平均数为
( 5×2+10×6+15×14+20×12+25×8+30×3)÷45
= 18(min).
将这45 个数由小到大排列,第23个数据是20min,
所以中位数为20min.
所用时间出现最多的是15 min,所以众数是15 min.
统计全班45名学生每天回家路上所用的时间。如果时间取最接近5的倍数的整数,那么整理后的数据如下表:
求所用时间的平均数、中位数和众数。
所用时间/min
5
10
15
20
25
30
合计
人数/名
2
6
14
12
8
3
45
例5
归纳总结
典例精析
众数是当一组数据中某一数据重复出现较多时,人
们往往关心的一个量,众数不受极端值的影响,这是它
的一个优势,缺点是当众数有多个且众数的频数相对较
小时可靠性小,局限性大.
中位数仅与数据的排列位置有关,不易受极端值影
响,中位数可能出现在所给数据中,也可能不在所给的
数据中.当一组数据中的个别数据变动较大时,可用中
位数描述其趋势,中位数的计算很少.
典例精析
中等水平
多数水平
典例精析
例6
某班50名学生中,13岁6人,14岁的25人,15岁的16人,16岁的3人.那么,这个班同 学年龄的众数和中位数分别是( )
A、13,16 B、14,11 C、14,14 D、14,16
C
数据
13岁
14岁
15岁
16岁
出现次数
6人
25人
16人
3人
排序:
13,…,13, 14,…,14, 15,…,15, 16,…,16
6个
25个
16个
3个
典例精析
例7
某公司的43名职工的月工资(以元为单位)如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}职员
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
30
工资
5500
5000
3500
3000
2500
2000
1500
(1)求该公司职员月工资的平均数、中位数、众数?(精确到元)
解:1953 、1500、1500;
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数、中位数、众数又是什么?(精确到元)
解:2872、1500、1500;
典例精析
例7
某公司的43名职工的月工资(以元为单位)如下:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}职员
董事长
副董事长
董事
总经理
经理
管理员
职员
人数
1
1
2
1
5
3
30
工资
5500
5000
3500
3000
2500
2000
1500
(3)你认为应该使用平均数和中位数中哪一个来描述该公司职工的工资水平?
解析:(3)中位数或众数均能反映该公司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数与中位数偏差较大,所以平均数不能反映这个公司员工的工资水平.
典例精析
例8
七年级(6)班三位同学最近的五次数学测验
成绩(单位:分)分别是:
他们都认为自己的数学成绩比其他两位同学好,他们比较的依据分别是什么?
解: 小华成绩的众数是_____,中位数是_____,平均数是_____;
小明成绩的众数是_____,中位数是_____,平均数是_____;
小丽成绩的众数是_____,中位数是_____,平均数是_____.
98
62
95
98
89.4
84.2
99
85
77
因为他们之中,小华的平均数最大,小明的中位数最大,
小丽的众数最大,所以都认为自己的成绩比其他两位同学好.
小华 62 94 95 98 98
小明 62 62 98 99 100
小丽 40 62 85 99 99
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均的月销售额是多少?
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
解:(1)样本数据的众数是_____,中位数是_____,平均数约是_____.
可以推测,这个电商营销部营业员的月销售额为_____万元的人数最多,
中间的月销售额是____万元,平均月销售额大约是____万元.
15
15
18
18
20
20
销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
1
2
2
3
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
20
20
大
三分之一
解:(2)这个目标可以定为每月____万元(平均数).因为从样本数据看,在平均数、中位数和众数中,平均数最____.可以估计,月销售额定为每月____万元是一个较高的目标,大约会有___________的营业员获得奖励.
典例精析
例9
某电商营销部为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,电商营销部统计了每个营业员在某月的销售额(单位:万元),数据如下:
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
17 18 16 13 24 15 28 26 18 19
22 17 16 19 32 30 16 14 15 26
15 32 23 17 15 15 28 28 16 19
解:(3)月销售额可以定为每月____万元(中位数).因为从样本情况看,月销售额在____万元以上(含18万元)的有16人,占总人数的一半左右.可以估计,如果月销售额定为____万元,将有一半左右的营业员获得奖励.
18
18
18
典例精析
例10
下面是某校七年级(6)班两组女生的体重(单位:kg):
(1)分别求这两组数据的平均数、众数、中位数,并解释它们的实际意义(结果取整数);
(2)比较这两组数据的平均数、众数、中位数,谈谈你对它们的认识 .
解:(1)第1组数据的平均数是44,众数是42,中位数是40;
第2组数据的平均数约为40,众数是42,中位数是40.
(2)这两组数据中,只有一个数据不同,第1组是75,第2组是45,
因此这两组数据的平均数不同,但它们的中位数和众数相同.
由此可以看出,平均数受极值的影响较大,中位数和众数不受极值的影响.
第1组 35 36 38 40 42 42 75
第2组 35 36 38 40 42 42 45
归纳总结
中位数和众数
中位数:中间的一个数,或中间的两个数的平均数.
众数:出现次数最多的数.
平均数、中位数、众数的特征:平均数是最常用的指标,它表示“一般水平”,中位数表示“中等水平”,众数表示“多数水平”.
当堂检测
课堂练习
1.某单位若干名职工参加普法知识竞赛,将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些职工成绩的中位数和平均数分别是( )
A.94分,96分
B.96分,96分
C.94分,96.4分
D.96分,96.4分
D
当堂检测
2.数据1,2, 8,5,3,9,5,4,5,4的众数、中位数分别为(???? )
A.4.5、5?? ??B.5、4.5?? ??C.5、4??? ??D.5、5?
3.在演讲比赛中,你想知道自己在所有选手中处于什么水平,应该选择哪个数据的代表( )
A.平均数?? B.中位数??? C.众数
B
B
4.已知一组数据:x1=4,x2=5,x3=6,x4=7,它们出现的次数依次为2,3,2,1,则这组数据的众数为 ,中位数为 ,平均数为 .
5
5
5.25
当堂检测
5.根据实际情况填写(填平均数、中位数、众数)
①老板进货时关注卖出商品的 .
②评委给选手综合得分时关注 .
③被招聘的员工关注公司员工工资的 .
中位数
平均数
众数
6.公园里有甲、乙两群游客正在做团体游戏,两群游客的年龄如下:
甲群:13、13、14、15、15、15、16、17、17.
乙群:3、4、4、5、5、6、6、54、57.
(1)甲群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映甲群游客年龄特征的是 .
(2)乙群游客的平均年龄是 岁,中位数是 岁,众数是 岁,其中能较好反映乙群游客年龄特征的是 .
15
15
15
16
4、5、6
5
众数
众数
当堂检测
7.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元/人.年)如下表所示:
部门
A
B
C
D
E
F
G
人数
1
1
2
4
2
2
3
利润
20
5
2.5
2.1
1.5
1.5
1.2
根据表中提供的信息填空:
(1)该公司每人所创年利润的平均数是( )
万元,中位数是( )万元,众数是( )万元.
(2)你认为应该使用平均数还是中位数来描述该公司每人所创年利润的一般水平?
3.2
2.1
1.5和2.1
中位数
当堂检测
课堂练习
8.为了了解开展“孝敬父母,从家务事做起”活动的实施情况,某校抽取八年级某班50名学生,调查他们一周做家务所用时间,得到一组数据,并绘制成下表,请根据下表完成各题:
每周做家务的时间(小时)
0
1
1.5
2
2.5
3
3.5
4
人数
2
2
6
12
13
4
3
(1)填写图表格中未完成的部分;
(2)该班学生每周做家务的平均时间是 .
2.44
(3)这组数据的中位数是 ,众数是 .
2.5
3
8
