23.3等可能事件概率计算公式(第2课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 23.3等可能事件概率计算公式(第2课时)(教学课件)-2023-2024学年八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 14:05:59 | ||
图片预览











文档简介
2023-2024学年八年级下册数学同步精品课堂(沪教版)
23.3等可能事件概率计算公式(第2课时)
第 23章 概率初步
学习目标
1.通过实例理解等可能性试验的概念.
2.掌握等可能试验中事件的概率计算公式.(重点)
3.会运用公式计算简单的概率.(难点)
摸牌试验:在一副扑克牌中取红桃、梅花、方块各一张牌混合放在一起,从中任意摸出一张牌是红桃的概率为 ????????.
?
原因在于:
任意一次试验的结果只有三种:
即摸出红桃、摸出梅花或摸出方块;
同时这三种结果出现的机会均等;
而且一次试验中不会同时出现两种结果.
如果一项可以反复进行的试验具有以下特点:
(1) 试验的结果是有限个;
(2) 各种结果可能出现的机会是均等的;
(3) 任何两个结果不可能同时出现.
那么这样的试验叫做“等可能试验”.
1.掷一枚材质均匀的骰子,看结果那个面朝上,这个试验是等可能试验吗?
解:在掷一枚骰子的试验中,所有可能出现的结果只有六种,分别是“出现1点”,“出现2点”,……,“出现6点”。由于骰子的质地均匀,随手掷出骰子,可以认为各种结果出现的机会均等,所以这个试验是等可能试验。
解:从2个红球、1个白球中任意摸出一个球来,“摸到红球”和“摸到白球”并不是等可能试验。要把2个红球编号,分别为红1、红2,那么“摸到红1”,“摸到红2”和“摸到白球”才是等可能试验。
注意等可能试验必须具备的条件,即:
1.试验结果个数有限;
2.每次试验结果唯一;
3.每个试验结果都等可能。
2.从2个红球、1个白球中任意摸出一个球来,“摸到红球”和“摸到白球”是等可能试验吗?
3.判断以下说法是否正确:
同时掷两枚硬币有3种结果,两正、两反和一正一反,所以掷出一正一反的概率是 .
1
3
注意等可能试验必须具备的条件,即:
1.试验结果个数有限;
2.每次试验结果唯一;
3.每个试验结果都等可能。
“两正”、“两反”和“一正一反”是3个随机事件,它们不是等可能试验
等可能试验中:某个事件的概率计算公式
一般地,如果一个试验共有n个等可能的结果,事件A包含其中的k个结果,那么事件A的概率是:
例1.甲乙两人轮流掷一枚材质均匀的骰子,每人各掷了8次.结果甲有三次掷得"合数点",而乙没有一次掷得"合数点",如果两人继续掷,那么下一次谁掷得"合数点"的机会比较大?
解:掷一枚骰子的试验是等可能试验,共有6个等可能结果."掷得合数点"的事件包含"4点""6点"两个结果,所以"掷得合数点"的概率为26,即13.
因为在每一次掷骰子的试验中,事件"掷得合数点"的概率是不变的,所以两人下一次掷得合数点的机会一样大.
?
议一议:“掷一枚骰子得合数点”这个事件的概率是三分之一,为什么乙掷8次却没有一次掷得“合数点”?
例2.在一副扑克牌中拿出2张红桃、2张黑桃的牌共4张,洗匀后,从中任取2张牌恰好同花色的概率是多少?
解:解法一:把拿出的4张牌编号,如红桃1、红桃2、黑桃1、黑桃2.从中任取2张牌的试验,是等可能试验.
试验出现的等可能结果共有6个:
“红桃1、红桃2”;“红桃1、黑桃1”;“红桃1、黑桃2”;“红桃2、黑桃1”;"红桃2、黑桃2";"黑桃1、黑桃2".
设事件 A :“2张牌恰好同花色”,它包含其中2个结果:
"红桃1、红桃2":"黑桃1、黑桃2“.
所以, P ( A )=26=13.
?
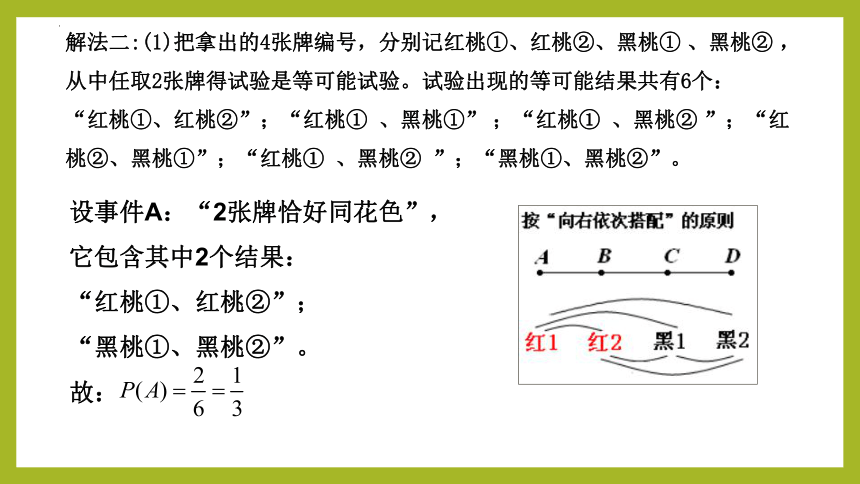
解法二:(1)把拿出的4张牌编号,分别记红桃①、红桃②、黑桃① 、黑桃② ,从中任取2张牌得试验是等可能试验。试验出现的等可能结果共有6个:
“红桃①、红桃②”;“红桃① 、黑桃①” ;“红桃① 、黑桃② ”;“红桃②、黑桃①”;“红桃① 、黑桃② ”;“黑桃①、黑桃②”。
设事件A:“2张牌恰好同花色”,
它包含其中2个结果:
“红桃①、红桃②”;
“黑桃①、黑桃②”。
故:
议一议:如果“拿出3张红桃、2张黑桃;洗匀后,从中任取2张牌恰好同花色的概率是多少”?
1
2
3
8
红1
红2
红3
黑1
黑2
9
4
10
5
6
7
如图共有(红1红2),(红1红3),(红1黑1),(红1黑2),(红2红3).(红2黑1),(红2黑2)(红3黑1),(红3黑2)(黑1黑2)这10种结果。
其中(红1红2),(红1红3),(红2红3),(黑1黑2)是同花色的,因此求得的概率是
例3 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
归纳总结
例4: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
例3.同时掷两个质地均匀的骰子,计算下列事件的概率:(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
1
2
3
4
5
6
1
2
3
4
5
6
第
一
个
第
二
个
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等。
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则P(A)= =
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则P(B)= =
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则P(C)=
例5 甲乙两人要去风景区游玩,仅直到每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,当不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲乙两人分别会乘坐的汽车列表如下:
顺序
甲
乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘坐到上等汽车的概率是 ,乘坐到下等汽车的概率只有
答:乙的乘车办法有有利于乘上舒适度较好的车.
1.有人说如果随机事件 A 的概率 P(A)=0.5,那么由 P(A)X20.5X2=1,可知在相同的条件下重复 2 次,事件 A 肯定发生.你认为他的说法对吗?
2.布袋里有 2 个红球、3 个黄球、4 个白球,它们除颜色外其他都相同.从布袋里摸出一个球恰好为红球的概率是多少?
3.掷一枚材质均匀的骰子,掷得的点数为素数的概率是多少?
课本练习
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
随堂检测
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)=
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
第
一
张
第
二
张
解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
课堂小结
本节主要研究了等可能试验的概率求法,解题时要注意两点:
(1)条件:试验结果的有限性和所有结果的等可能性。
(2)解题步骤;
①求出总的所有可能结果数;
②求出事件A所包含的可能结果数,然后利用公式
注意:等可能试验的每一次试验都是独立的,不会受前几次的试验结果影响其下一次的概率.
23.3等可能事件概率计算公式(第2课时)
第 23章 概率初步
学习目标
1.通过实例理解等可能性试验的概念.
2.掌握等可能试验中事件的概率计算公式.(重点)
3.会运用公式计算简单的概率.(难点)
摸牌试验:在一副扑克牌中取红桃、梅花、方块各一张牌混合放在一起,从中任意摸出一张牌是红桃的概率为 ????????.
?
原因在于:
任意一次试验的结果只有三种:
即摸出红桃、摸出梅花或摸出方块;
同时这三种结果出现的机会均等;
而且一次试验中不会同时出现两种结果.
如果一项可以反复进行的试验具有以下特点:
(1) 试验的结果是有限个;
(2) 各种结果可能出现的机会是均等的;
(3) 任何两个结果不可能同时出现.
那么这样的试验叫做“等可能试验”.
1.掷一枚材质均匀的骰子,看结果那个面朝上,这个试验是等可能试验吗?
解:在掷一枚骰子的试验中,所有可能出现的结果只有六种,分别是“出现1点”,“出现2点”,……,“出现6点”。由于骰子的质地均匀,随手掷出骰子,可以认为各种结果出现的机会均等,所以这个试验是等可能试验。
解:从2个红球、1个白球中任意摸出一个球来,“摸到红球”和“摸到白球”并不是等可能试验。要把2个红球编号,分别为红1、红2,那么“摸到红1”,“摸到红2”和“摸到白球”才是等可能试验。
注意等可能试验必须具备的条件,即:
1.试验结果个数有限;
2.每次试验结果唯一;
3.每个试验结果都等可能。
2.从2个红球、1个白球中任意摸出一个球来,“摸到红球”和“摸到白球”是等可能试验吗?
3.判断以下说法是否正确:
同时掷两枚硬币有3种结果,两正、两反和一正一反,所以掷出一正一反的概率是 .
1
3
注意等可能试验必须具备的条件,即:
1.试验结果个数有限;
2.每次试验结果唯一;
3.每个试验结果都等可能。
“两正”、“两反”和“一正一反”是3个随机事件,它们不是等可能试验
等可能试验中:某个事件的概率计算公式
一般地,如果一个试验共有n个等可能的结果,事件A包含其中的k个结果,那么事件A的概率是:
例1.甲乙两人轮流掷一枚材质均匀的骰子,每人各掷了8次.结果甲有三次掷得"合数点",而乙没有一次掷得"合数点",如果两人继续掷,那么下一次谁掷得"合数点"的机会比较大?
解:掷一枚骰子的试验是等可能试验,共有6个等可能结果."掷得合数点"的事件包含"4点""6点"两个结果,所以"掷得合数点"的概率为26,即13.
因为在每一次掷骰子的试验中,事件"掷得合数点"的概率是不变的,所以两人下一次掷得合数点的机会一样大.
?
议一议:“掷一枚骰子得合数点”这个事件的概率是三分之一,为什么乙掷8次却没有一次掷得“合数点”?
例2.在一副扑克牌中拿出2张红桃、2张黑桃的牌共4张,洗匀后,从中任取2张牌恰好同花色的概率是多少?
解:解法一:把拿出的4张牌编号,如红桃1、红桃2、黑桃1、黑桃2.从中任取2张牌的试验,是等可能试验.
试验出现的等可能结果共有6个:
“红桃1、红桃2”;“红桃1、黑桃1”;“红桃1、黑桃2”;“红桃2、黑桃1”;"红桃2、黑桃2";"黑桃1、黑桃2".
设事件 A :“2张牌恰好同花色”,它包含其中2个结果:
"红桃1、红桃2":"黑桃1、黑桃2“.
所以, P ( A )=26=13.
?
解法二:(1)把拿出的4张牌编号,分别记红桃①、红桃②、黑桃① 、黑桃② ,从中任取2张牌得试验是等可能试验。试验出现的等可能结果共有6个:
“红桃①、红桃②”;“红桃① 、黑桃①” ;“红桃① 、黑桃② ”;“红桃②、黑桃①”;“红桃① 、黑桃② ”;“黑桃①、黑桃②”。
设事件A:“2张牌恰好同花色”,
它包含其中2个结果:
“红桃①、红桃②”;
“黑桃①、黑桃②”。
故:
议一议:如果“拿出3张红桃、2张黑桃;洗匀后,从中任取2张牌恰好同花色的概率是多少”?
1
2
3
8
红1
红2
红3
黑1
黑2
9
4
10
5
6
7
如图共有(红1红2),(红1红3),(红1黑1),(红1黑2),(红2红3).(红2黑1),(红2黑2)(红3黑1),(红3黑2)(黑1黑2)这10种结果。
其中(红1红2),(红1红3),(红2红3),(黑1黑2)是同花色的,因此求得的概率是
例3 同时抛掷2枚均匀的骰子一次,骰子各面上的点数分别是1,2,···,6.试分别计算如下各随机事件的概率.
(1)抛出的点数之和等于8;
(2)抛出的点数之和等于12.
分析:首先要弄清楚一共有多少个可能结果.第1枚骰子可能掷出1,2,···,6中的每一种情况,第2枚骰子也可能掷出1,2,···,6中的每一种情况.可以用“列表法”列出所有可能的结果如下:
第2枚
骰子
第1枚骰子
结
果
1
2
3
4
5
6
1
2
3
4
5
6
(1,1)
(1,2)
(1,3)
(1,4)
(1,5)
(1,6)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(2,2)
(2,3)
(2,4)
(2,5)
(2,6)
(3,2)
(3,3)
(3,4)
(3,5)
(3,6)
(4,2)
(5,2)
(6,2)
(4,3)
(5,3)
(6,3)
(4,4)
(5,4)
(6,4)
(4,5)
(5,5)
(6,5)
(4,6)
(5,6)
(6,6)
解:从上表可以看出,同时抛掷两枚骰子一次,所有可能出现的结果有36种.由于骰子是均匀的,所以每个结果出现的可能性相等.
(1)抛出点数之和等于8的结果有(2,6),(3,5),(4,4),(5,3)和(6,2)这5种,所以抛出的点数之和等于8的这个事件发生的概率为
(2)抛出点数之和等于12的结果仅有(6,6)这1种,所以抛出的点数之和等于12的这个事件发生的概率为
当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能结果,通常采用列表法.
归纳总结
例4: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后放回袋中并搅匀,再从中任意摸出一个球,两次都摸出红球的概率是多少?
1
2
结果
第一次
第二次
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,白)
(白,红1)
(白,红2)
(红1,白)
(红1,红1)
(红1,红2)
(红2,白)
(红2,红1)
(红2,红2)
变式:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,记录下颜色后不再放回袋中,再从中任意摸出一个球,两次都摸出红球的概率是多少?
解:利用表格列出所有可能的结果:
白
红1
红2
白
红1
红2
(白,红1)
(白,红2)
(红1,白)
(红1,红2)
(红2,白)
(红2,红1)
结果
第一次
第二次
例3.同时掷两个质地均匀的骰子,计算下列事件的概率:(1)两个骰子的点数相同
(2)两个骰子的点数之和是9
(3)至少有一个骰子的点数为2
1
2
3
4
5
6
1
2
3
4
5
6
第
一
个
第
二
个
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
解:由列表得,同时掷两个骰子,可能出现的结果有36个,它们出现的可能性相等。
(1)满足两个骰子的点数相同(记为事件A)的结果有6个,则P(A)= =
(2)满足两个骰子的点数之和是9(记为事件B)的结果有4个,则P(B)= =
(3)满足至少有一个骰子的点数为2(记为事件C)的结果有11个,则P(C)=
例5 甲乙两人要去风景区游玩,仅直到每天开往风景区有3辆汽车,并且舒适程度分别为上等、中等、下等3种,当不知道怎样区分这些车,也不知道它们会以怎样的顺序开来.于是他们分别采用了不同的乘车办法:甲乘第1辆开来的车.乙不乘第1辆车,并且仔细观察第2辆车的情况,如比第1辆车好,就乘第3辆车.试问甲、乙两人的乘车办法,哪一种更有利于乘上舒适度较好的车?
解:容易知道3辆汽车开来的先后顺序有如下6种可能情况:
(上中下),
(上下中),
(上下),
(中下上),
(下上中),
(下中上).
假定6种顺序出现的可能性相等, 在各种可能顺序之下,甲乙两人分别会乘坐的汽车列表如下:
顺序
甲
乙
上中下
上下中
中上下
中下上
下上中
下中上
上
下
上
中
中
上
中
上
下
上
下
中
甲乘到上等、中等、下等3种汽车的概率都是 ;
乙乘坐到上等汽车的概率是 ,乘坐到下等汽车的概率只有
答:乙的乘车办法有有利于乘上舒适度较好的车.
1.有人说如果随机事件 A 的概率 P(A)=0.5,那么由 P(A)X20.5X2=1,可知在相同的条件下重复 2 次,事件 A 肯定发生.你认为他的说法对吗?
2.布袋里有 2 个红球、3 个黄球、4 个白球,它们除颜色外其他都相同.从布袋里摸出一个球恰好为红球的概率是多少?
3.掷一枚材质均匀的骰子,掷得的点数为素数的概率是多少?
课本练习
1.小明与小红玩一次“石头、剪刀、布”游戏,则小明赢的概率是( )
2.某次考试中,每道单项选择题一般有4个选项,某同学有两道题不会做,于是他以“抓阄”的方式选定其中一个答案,则该同学的这两道题全对的概率是( )
C
D
A. B. C. D.
A. B. C. D.
随堂检测
3.如果有两组牌,它们的牌面数字分别是1,2,3,那么从每组牌中各摸出一张牌.
(1)摸出两张牌的数字之和为4的概念为多少?
(2)摸出为两张牌的数字相等的概率为多少?
3
2
(2,3)
(3,3)
(3,2)
(3,1)
(2,2)
(2,1)
(1,3)
(1,2)
(1,1)
1
3
2
1
第二张牌
的牌面数字
第一张牌的
牌面数字
解:(1)P(数字之和为4)= .
(2)P(数字相等)=
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
1
2
3
4
5
6
1
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
2
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
3
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
4
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
5
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
6
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
第
一
张
第
二
张
解:由列表得,两次抽取卡片后,可能出现的结果有36个,它们出现的可能性相等.
满足第一次取出的数字能够整除第二次取出的数字(记为事件A)的结果有14个,则
P(A)= =
4.在6张卡片上分别写有1-6的整数,随机地抽取一张后放回,再随机地抽取一张,那么第一次取出的数字能够整除第二次取出的数字的概率是多少?
课堂小结
本节主要研究了等可能试验的概率求法,解题时要注意两点:
(1)条件:试验结果的有限性和所有结果的等可能性。
(2)解题步骤;
①求出总的所有可能结果数;
②求出事件A所包含的可能结果数,然后利用公式
注意:等可能试验的每一次试验都是独立的,不会受前几次的试验结果影响其下一次的概率.
