(期末大通关)第六单元简易方程必考题检测卷(单元测试)2023-2024学年数学五年级下册苏教版(含答案)
文档属性
| 名称 | (期末大通关)第六单元简易方程必考题检测卷(单元测试)2023-2024学年数学五年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 508.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 19:53:41 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
(期末大通关)第六单元简易方程必考题检测卷(单元测试)2023-2024学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.面积最接近100平方厘米的是( )。
A.一个成人的手掌面 B.一本六年级数学课本的封面
C.一枚1元硬币的正面 D.一张课桌的桌面
2.在如图的图形中,共有( )对称轴。
A.2条 B.4条 C.8条 D.无数条
3.如果一个圆面积扩大到原来的25倍,则它的周长随着扩大到原来的( )。
A.2倍 B.25倍 C.5倍 D.无法确定
4.要剪一张周长是12.56厘米的圆形纸片,至少需要面积是( )平方厘米的正方形纸片。
A.12.56 B.14 C.16 D.20
5.小明从A地到B地有两条路线可走(如图),( )。
A.走①号路线近 B.走②号路线近 C.①号路线和②号路线一样近 D.无法比较
6.用一张长是8厘米,宽5厘米的长方形纸最多可以剪( )个直径是2厘米的圆。
A.4 B.2 C.6 D.8
7.星期天,小林去游乐场游玩,摩天轮的半径是50米,小林坐着它转动一周,大约在空中转过( )米。(π取3.14)
A.157 B.314 C.78.5 D.7850
8.公园管理处要在一棵大榕树周围安装围树环形座椅(见示意图)。他们用一根绳子绕树干10圈,量得结果是18.84米。应选购下面( )种座椅。
A.内圆直径50厘米,外圆直径130厘米 B.内圆直径60厘米,外圆直径1.4米
C.内圆直径1米,外圆直径1.8米 D.内圆直径6米,外圆直径6.8米
二、填空题
9.一个半圆的半径是4厘米,那么它的周长是( )厘米。
10.如果大圆直径是小圆半径的4倍,那么大圆周长是小圆周长的( )倍。
11.用一根铁丝正好可以围成一个边长为6.28米的正方形,如果用这根铁丝围成一个圆,这个圆的直径是( )米。
12.在解决“已知圆的半径为3厘米,求圆的面积”这个问题时,有一位同学忘记了圆的面积计算公式,他便回忆圆的面积公式推导过程,分步求出了结果。第一步:2×3.14×3=18.84(厘米),第二步:18.84÷2=9.42(厘米),第三步:( )。
13.如图,把一个圆切拼成一个近似的长方形,已知圆的半径是2厘米,阴影部分的面积是( )平方厘米。
14.在一个圆中画一个最大的正方形,这个正方形的面积是20平方厘米,这个圆的面积是( )。
三、判断题
15.所有的直径(或半径)都相等。( )
16.世界上第一个把圆周率的值精确到小数点后7位的科学家是刘徽。( )
17.一条弧和两条半径就能组成一个扇形。( )
18.两个圆只要半径相等就可以说它的形状和大小完全一样。( )
19.圆的周长÷直径=3.14。( )
四、计算题
20.求图形中阴影部分的周长和面积。(单位:厘米)
21.求阴影部分的面积。
五、解答题
22.将一张长6分米、宽4分米的长方形花布剪成一个最大的半圆,再给这个半圆花布缝个花边,花边耗损1分米,至少要买多长的花边?
23.一个圆形广场,直径是200米。在广场的四周每隔4米摆一盆花,一共需要摆多少盆花?
24.有三根圆柱形的钢管,横截面的半径都为2分米。现在用绳子进行捆扎。如图为捆扎的横截面示意图,请你算一算这种捆扎方式所用绳子的长度是多少分米?(接头处忽略不计。〕
25.一个圆形花圃,小强沿着它的边线走一圈,一共走了314步。已知小强的平均步长是0.6米。
(1)如果沿着花圃边线每隔1.2米栽一棵杜鹃花,一共要栽多少棵?
(2)这个花圃的占地面积是多少平方米?
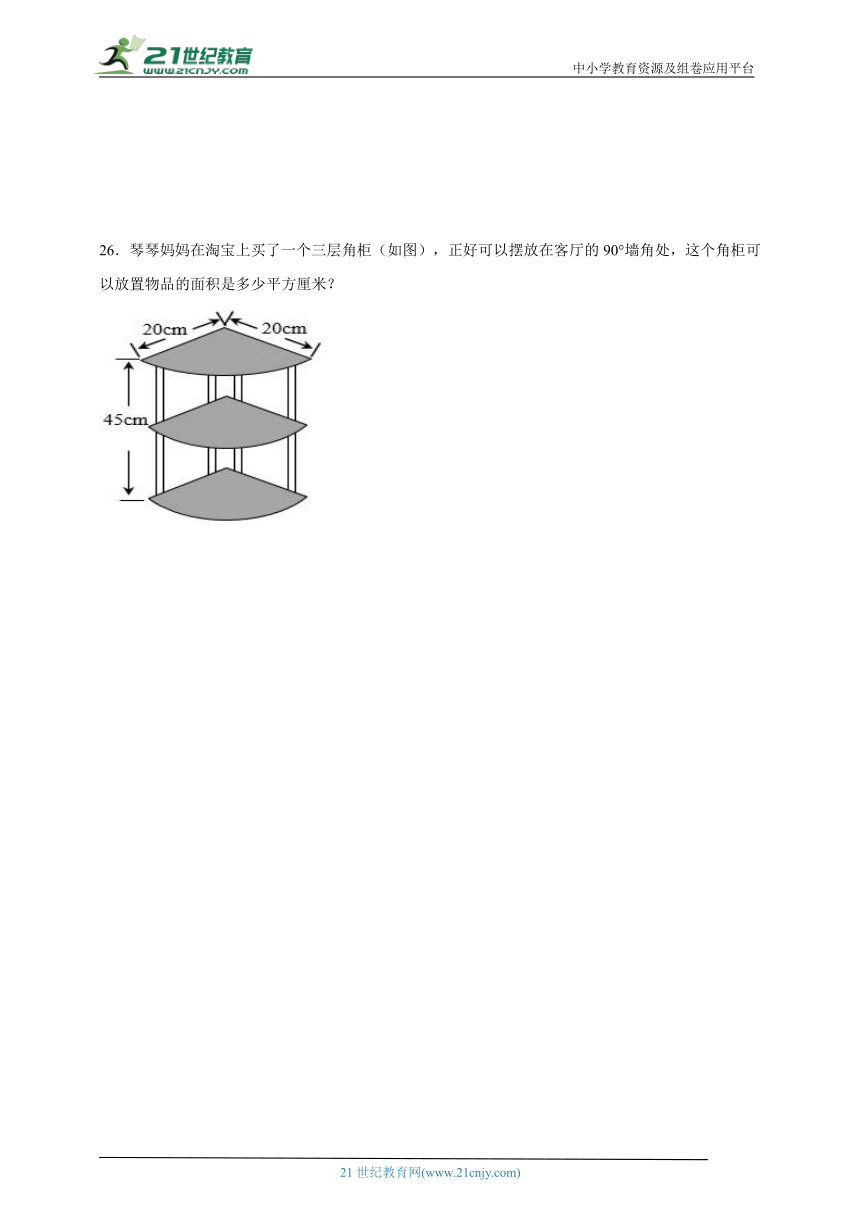
26.琴琴妈妈在淘宝上买了一个三层角柜(如图),正好可以摆放在客厅的90°墙角处,这个角柜可以放置物品的面积是多少平方厘米?
参考答案:
1.A
【分析】边长为10厘米的正方形的面积是100平方厘米,联系生活实际情况,结合数值的大小进行判断。
【详解】A.一个成人的手掌面的面积接近100平方厘米,符合题意;
B.一本六年级数学课本的封面近似看作是一个长方形,其长和宽均大于10厘米,因此面积大于100平方厘米,不符合题意;
C.一枚1元硬币的正面是一个圆形,其直径不到3厘米,因此面积远小于100平方厘米,不符合题意;
D.一张课桌的桌面看作是一个长方形,其长和宽均超过10厘米,因此面积超过100平方厘米,不符合题意。
故答案为:A
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。圆的对称轴有无数条,正方形的对称轴有4条,圆和正方形组合后,只有4条对称轴。据此解答。
【详解】
有4对称轴。
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.C
【分析】由圆半径与直径的关系“”、圆周长计算公式“”、圆面积计算公式“”可知,一个圆的半径扩大到原来的多少倍,它的直径、周长也扩大相同的倍数,面积则扩大这个倍数的平方倍,据此可解答。
【详解】因为,
所以一个圆面积扩大到原来的25倍,则它的周长随着扩大到原来的5倍;
故答案为:C
【点睛】一个圆的半径扩大多少倍,它的直径、周长也扩大相同的倍数,面积则扩大这个倍数的平方倍。
4.C
【分析】当圆的直径是正方形的边长时,此时正方形的面积最小。根据圆的周长=πd,计算出圆的直径,此时圆的直径即为正方形的边长;根据正方形的面积=边长×边长,代入数值计算即可。
【详解】圆的直径:12.56÷3.14=4(厘米)
正方形的面积:4×4=16(平方厘米)
因此要剪一张周长是12.56厘米的圆形纸片,至少需要面积是16平方厘米的正方形纸片。
故答案为:C
5.C
【分析】如图,假设三条直径分别是d1、d2、d3,根据圆周长的一半=π×直径÷2,分别表示出两条路线的长度,比较即可。
【详解】①号路线:3.14×(d1+d2+d3)÷2=1.57×(d1+d2+d3)
②号路线:3.14×d1÷2+3.14×d2÷2+3.14×d3÷2
=3.14÷2×(d1+d2+d3)
=1.57×(d1+d2+d3)
比较可知,①号路线和②号路线一样近。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
6.D
【分析】根据题意,沿着长方形的长能剪(10÷2=5) 个圆;5÷2=2 (个) ……1(厘米),沿着长方形的宽能剪2个圆, 所以共剪( 5×2=10 )个圆,据此解答。
【详解】8÷2=4(个)
5÷2=2 (个) ……1(厘米)
4×2=8(个)
所以,用一张长是8厘米,宽5厘米的长方形纸最多可以剪8个直径是2厘米的圆。
故答案为:D
【点睛】抓住在长方形内剪切圆的方法即可解答此类问题。
7.B
【分析】求摩天轮在空中转过的米数,就是求半径为50米的圆的周长;根据圆的周长公式C=2πr,代入数据计算即可。
【详解】2×3.14×50=314(米)
大约在空中转过314米。
故答案为:B
【点睛】本题考查圆的周长公式的运用,明白摩天轮旋转一周的距离即是圆的周长。
8.C
【分析】绳子长度÷10=大榕树周长,根据圆的直径=周长÷圆周率,求出榕树直径,安装的环形座椅的内圆应该比树的周长大一点,给大榕树成长的空间,据此选择。
【详解】18.84÷10=1.884(米)
1.884÷3.14=0.6(米)=60(厘米)
A.直径小于大榕树直径,安装不上,排除;
B.直径刚好等于大榕树直径,没有留出一定距离,排除;
C.直径大于大榕树直径一些,可以;
D.直径大于大榕树直径太多,不合适,排除。
应选购内圆直径1米,外圆直径1.8米种座椅。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
9.20.56
【分析】根据半圆的周长=圆周长的一半+两条半径,圆的周长=,代入求解即可。
【详解】2×3.14×4÷2+2×4
=6.28×4÷2+2×4
=25.12÷2+8
=12.56+8
=20.56(厘米)
即它的周长是20.56厘米。
【点睛】本题考查半圆的周长,注意加上2条半径。
10.2
【分析】根据圆的周长==,假设小圆半径是1,则大圆直径是4,分别求出周长即可解答。
【详解】假设小圆半径是1,则大圆直径是4
2×3.14×1
=6.28×1
=6.28
4×3.14=12.56
12.56÷6.28=2
即大圆周长是小圆周长的2倍。
【点睛】本题考查圆的周长,公式要重点掌握。
11.8
【分析】根据正方形边长计算公式“C=4a”即可求出这根铁丝的长度,再把这根铁丝围成一个圆时,即已知周长,根据圆周长计算公式“C=πd”求出围成的圆的直径即可。
【详解】6.28×4=25.12(米)
25.12÷3.14=8(米)
这个圆的直径是8米。
【点睛】解答此题的关键一是弄清题意;二是正方形周长、圆周长计算公式的灵活运用。
12.9.42×3=28.26(平方厘米)
【分析】第一步求的是圆的周长,将圆拼成一个长方形,这个时候长方形的长等于圆周长的一半,长方形的宽等于半径,圆的面积等于长方形的面积,第二步求的是圆周长的一半,也就是长方形的长,第三步求面积,长×宽=面积,据此解答即可。
【详解】由分析可得:
第一步求圆的周长:2×3.14×3=18.84(厘米)
第二步求圆的周长的一半:18.84÷2=9.42(厘米)
第三步求面积:9.42×3=28.26(平方厘米)
【点睛】考查圆的面积推导过程,重点是能够知道圆的周长一半等于长方形的长,圆的半径等于长方形的宽。
13.9.42
【分析】把圆转化成近似的长方形,所以这个长方形的面积就等于圆的面积,,据此解答。
【详解】(1-)×3.14×
=
=9.42(平方厘米)
所以阴影部分的面积是9.42平方厘米。
【点睛】本题考查圆面积公式的灵活运用,转化思想是关键。
14.31.4平方厘米/31.4cm2
【分析】如下图:
在圆内画一个最大的正方形,以圆的直径为正方形的对角线;设圆的半径为r厘米,则这个图形中的正方形的面积为2r2平方厘米,已知这个正方形的面积是20平方厘米,用20÷2即可求出r2;然后根据圆面积公式:S=πr2,用3.14×(20÷2)即可求出圆面积。据此解答。
【详解】解:设圆的半径为r厘米,
2r2=20
2r2÷2=20÷2
r2=10
3.14×10=31.4(平方厘米)
这个圆的面积是31.4平方厘米。
【点睛】本题考查方外圆的面积计算,明确半径和正方形面积之间的关系是解答本题的关键。
15.×
【分析】在同圆或等圆中,所有的直径(或半径)都相等;如果不限定是什么样的圆,那么这句话是错的,据此解答。
【详解】在同圆或等圆中,所有的直径(或半径)都相等;在不等的圆中,所有的直径(或半径)都不相等,因此这句话是错的。
故答案为:×
16.×
【分析】我国魏晋时期数学家刘徽求得圆周率的近似值是3.14。我国南北朝科学家祖冲之算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后7位的人。
【详解】世界上第一个把圆周率的值精确到小数点后7位的科学家是祖冲之。即原题说法错误。
故答案为:×
17.×
【分析】由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,是扇形。据此概念分析解题即可。
【详解】这两条半径可能长度不相等,也可能长度相等,如果和这条弧对应的半径长度不相等。那么任意的两条半径可能和指定的一条弧没有关系。所以一条弧和两条半径不一定能组成扇形。
故答案为:×
【点睛】本题考查了扇形,掌握扇形的定义是解题的关键。
18.√
【分析】根据圆的周长公式:C=2πr,根据圆的面积公式:S=πr2,由于当半径相等,π是固定值,所以周长相等,也就是形状相同;半径相等,那么半径的平方也是相同,所以大小也是一样,据此即可判断。
【详解】由分析可知:
两个圆只要半径相等就可以说它的形状和大小完全一样,说法正确。
故答案为:√
【点睛】本题主要考查圆的周长和面积公式,熟练掌握它的公式并灵活运用。
19.×
【分析】圆周率是指圆的周长与它直径的比值,叫做圆周率,圆周率用字母“π”表示,圆周率是一个无限不循环小数,它的取值即3.1415926到3.1415927之间,π≈3.14,据此解答。
【详解】圆的周长÷直接≈3.14。
原题干说法错误。
故答案为:×
【点睛】明确圆周率的意义是解答本题的关键。
20.周长:37.7厘米;面积:20.75平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-直径是10厘米圆的面积的一半;阴影部分的周长=长方形的两条宽+长方形的一条长+直径是10厘米圆的周长的一半,根据圆的面积公式:S=πr2,圆的周长公式:C=πd,长方形的面积=长×宽,据此进行计算即可。
【详解】阴影部分的周长:
6×2+10+3.14×10÷2
=12+10+15.7
=22+15.7
=37.7(厘米)
阴影部分的面积:
10×6-3.14×(10÷2)2÷2
=60-3.14×25÷2
=60-39.25
=20.75(平方厘米)
21.29.76cm2
【分析】观察图形可知,阴影部分面积=上底是6cm,下底是14cm,高是8cm的梯形面积-半径是(8÷2)cm的圆的面积,根据梯形面积公式:面积=(上底+下底)×高÷2;圆的面积公式:面积=π×半径2;代入数据,即可解答。
【详解】(6+14)×8÷2-3.14×(8÷2)2
=20×8÷2-3.14×16
=160÷2-50.24
=80-50.24
=29.76(cm2)
22.16.42分米
【分析】因为长方形的长为6分米,而要求剪下的是最大的半圆,所以根据长方形内最大的半圆的半径特点可知:这个半圆的直径就等于长方形的长,半径为6÷2=3(分米),3分米<4分米,所以最大的半圆的直径为6分米,则半圆的周长根据圆的周长公式:C=πd,即可求解。
【详解】6÷2=3(分米)
3<4
3×3.14+3×2+1
=9.42+6+1
=15.42+1
=16.42(分米)
答:至少要买16.42分米的花边。
【点睛】解答此题的关键是明白:这个半圆的直径是6分米。
23.157盆
【分析】在封闭线路上植树,棵数与段数相等,即:棵数=间隔数。圆形广场就是封闭图形,有几个4米,就摆几盆花。根据圆的周长=,求出圆的周长即可解答。
【详解】3.14×200÷4
=628÷4
=157(盆)
答:一共需要摆157盆花。
【点睛】本题考查圆的周长,公式要重点掌握。
24.24.56分米
【分析】如图所示,这种捆扎方式所用绳子的长度刚好是1个圆的周长加上3条直径的长,根据圆的周长=πd,代入数值计算即可解答。
【详解】3.14×2×2+2×2×3
=3.14×4+4×3
=12.56+12
=24.56(分米)
答:这种捆扎方式所用绳子的长度是24.56分米。
【点睛】解答本题的关键是观察分析圆柱钢管放置的特征,再结合圆的周长计算公式来求解。
25.(1)
【分析】(1)用每步的长度乘步数,即可求出总长度,即为圆的周长,根据圆环的植树问题可知,棵数=间隔数,用总长度除以间隔的长度,即可解答;
(2)根据“圆的周长公式:”,求出圆的半径,再根据“圆的面积公式:”代入数值,即可求出这个花圃的占地面积。
【详解】(1)314×0.6÷1.2
=188.4÷1.2
=157(棵)
答:一共要栽157棵。
(2)314×0.6÷3.14÷2
=188.4÷3.14÷2
=60÷2
=30(米)
3.14×302
=3.14×900
=2826(平方米)
答:这个花圃的占地面积是2826平方米。
【点睛】本题考查植树问题的计算及圆的周长和面积公式的应用。理解题意,找出数量关系,列式计算即可。
26.942平方厘米
【分析】每个扇形的圆心角都是90°,那么每个这样的扇形的面积相当于半径是20厘米的圆面积的四分之一,根据圆的面积公式:,求出圆的面积再除以4即可计算出一层的面积,再乘3即可。
【详解】3.14×202÷4×3
=3.14×400÷4×3
=1256÷4×3
=314×3
=942(平方厘米)
答:这个角柜可以放置物品的面积是942平方厘米。
【点睛】此题主要考查圆的面积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(期末大通关)第六单元简易方程必考题检测卷(单元测试)2023-2024学年数学五年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.面积最接近100平方厘米的是( )。
A.一个成人的手掌面 B.一本六年级数学课本的封面
C.一枚1元硬币的正面 D.一张课桌的桌面
2.在如图的图形中,共有( )对称轴。
A.2条 B.4条 C.8条 D.无数条
3.如果一个圆面积扩大到原来的25倍,则它的周长随着扩大到原来的( )。
A.2倍 B.25倍 C.5倍 D.无法确定
4.要剪一张周长是12.56厘米的圆形纸片,至少需要面积是( )平方厘米的正方形纸片。
A.12.56 B.14 C.16 D.20
5.小明从A地到B地有两条路线可走(如图),( )。
A.走①号路线近 B.走②号路线近 C.①号路线和②号路线一样近 D.无法比较
6.用一张长是8厘米,宽5厘米的长方形纸最多可以剪( )个直径是2厘米的圆。
A.4 B.2 C.6 D.8
7.星期天,小林去游乐场游玩,摩天轮的半径是50米,小林坐着它转动一周,大约在空中转过( )米。(π取3.14)
A.157 B.314 C.78.5 D.7850
8.公园管理处要在一棵大榕树周围安装围树环形座椅(见示意图)。他们用一根绳子绕树干10圈,量得结果是18.84米。应选购下面( )种座椅。
A.内圆直径50厘米,外圆直径130厘米 B.内圆直径60厘米,外圆直径1.4米
C.内圆直径1米,外圆直径1.8米 D.内圆直径6米,外圆直径6.8米
二、填空题
9.一个半圆的半径是4厘米,那么它的周长是( )厘米。
10.如果大圆直径是小圆半径的4倍,那么大圆周长是小圆周长的( )倍。
11.用一根铁丝正好可以围成一个边长为6.28米的正方形,如果用这根铁丝围成一个圆,这个圆的直径是( )米。
12.在解决“已知圆的半径为3厘米,求圆的面积”这个问题时,有一位同学忘记了圆的面积计算公式,他便回忆圆的面积公式推导过程,分步求出了结果。第一步:2×3.14×3=18.84(厘米),第二步:18.84÷2=9.42(厘米),第三步:( )。
13.如图,把一个圆切拼成一个近似的长方形,已知圆的半径是2厘米,阴影部分的面积是( )平方厘米。
14.在一个圆中画一个最大的正方形,这个正方形的面积是20平方厘米,这个圆的面积是( )。
三、判断题
15.所有的直径(或半径)都相等。( )
16.世界上第一个把圆周率的值精确到小数点后7位的科学家是刘徽。( )
17.一条弧和两条半径就能组成一个扇形。( )
18.两个圆只要半径相等就可以说它的形状和大小完全一样。( )
19.圆的周长÷直径=3.14。( )
四、计算题
20.求图形中阴影部分的周长和面积。(单位:厘米)
21.求阴影部分的面积。
五、解答题
22.将一张长6分米、宽4分米的长方形花布剪成一个最大的半圆,再给这个半圆花布缝个花边,花边耗损1分米,至少要买多长的花边?
23.一个圆形广场,直径是200米。在广场的四周每隔4米摆一盆花,一共需要摆多少盆花?
24.有三根圆柱形的钢管,横截面的半径都为2分米。现在用绳子进行捆扎。如图为捆扎的横截面示意图,请你算一算这种捆扎方式所用绳子的长度是多少分米?(接头处忽略不计。〕
25.一个圆形花圃,小强沿着它的边线走一圈,一共走了314步。已知小强的平均步长是0.6米。
(1)如果沿着花圃边线每隔1.2米栽一棵杜鹃花,一共要栽多少棵?
(2)这个花圃的占地面积是多少平方米?
26.琴琴妈妈在淘宝上买了一个三层角柜(如图),正好可以摆放在客厅的90°墙角处,这个角柜可以放置物品的面积是多少平方厘米?
参考答案:
1.A
【分析】边长为10厘米的正方形的面积是100平方厘米,联系生活实际情况,结合数值的大小进行判断。
【详解】A.一个成人的手掌面的面积接近100平方厘米,符合题意;
B.一本六年级数学课本的封面近似看作是一个长方形,其长和宽均大于10厘米,因此面积大于100平方厘米,不符合题意;
C.一枚1元硬币的正面是一个圆形,其直径不到3厘米,因此面积远小于100平方厘米,不符合题意;
D.一张课桌的桌面看作是一个长方形,其长和宽均超过10厘米,因此面积超过100平方厘米,不符合题意。
故答案为:A
2.B
【分析】轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线就是其对称轴。圆的对称轴有无数条,正方形的对称轴有4条,圆和正方形组合后,只有4条对称轴。据此解答。
【详解】
有4对称轴。
故答案为:B
【点睛】此题考查了轴对称的意义及在实际当中的运用。
3.C
【分析】由圆半径与直径的关系“”、圆周长计算公式“”、圆面积计算公式“”可知,一个圆的半径扩大到原来的多少倍,它的直径、周长也扩大相同的倍数,面积则扩大这个倍数的平方倍,据此可解答。
【详解】因为,
所以一个圆面积扩大到原来的25倍,则它的周长随着扩大到原来的5倍;
故答案为:C
【点睛】一个圆的半径扩大多少倍,它的直径、周长也扩大相同的倍数,面积则扩大这个倍数的平方倍。
4.C
【分析】当圆的直径是正方形的边长时,此时正方形的面积最小。根据圆的周长=πd,计算出圆的直径,此时圆的直径即为正方形的边长;根据正方形的面积=边长×边长,代入数值计算即可。
【详解】圆的直径:12.56÷3.14=4(厘米)
正方形的面积:4×4=16(平方厘米)
因此要剪一张周长是12.56厘米的圆形纸片,至少需要面积是16平方厘米的正方形纸片。
故答案为:C
5.C
【分析】如图,假设三条直径分别是d1、d2、d3,根据圆周长的一半=π×直径÷2,分别表示出两条路线的长度,比较即可。
【详解】①号路线:3.14×(d1+d2+d3)÷2=1.57×(d1+d2+d3)
②号路线:3.14×d1÷2+3.14×d2÷2+3.14×d3÷2
=3.14÷2×(d1+d2+d3)
=1.57×(d1+d2+d3)
比较可知,①号路线和②号路线一样近。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
6.D
【分析】根据题意,沿着长方形的长能剪(10÷2=5) 个圆;5÷2=2 (个) ……1(厘米),沿着长方形的宽能剪2个圆, 所以共剪( 5×2=10 )个圆,据此解答。
【详解】8÷2=4(个)
5÷2=2 (个) ……1(厘米)
4×2=8(个)
所以,用一张长是8厘米,宽5厘米的长方形纸最多可以剪8个直径是2厘米的圆。
故答案为:D
【点睛】抓住在长方形内剪切圆的方法即可解答此类问题。
7.B
【分析】求摩天轮在空中转过的米数,就是求半径为50米的圆的周长;根据圆的周长公式C=2πr,代入数据计算即可。
【详解】2×3.14×50=314(米)
大约在空中转过314米。
故答案为:B
【点睛】本题考查圆的周长公式的运用,明白摩天轮旋转一周的距离即是圆的周长。
8.C
【分析】绳子长度÷10=大榕树周长,根据圆的直径=周长÷圆周率,求出榕树直径,安装的环形座椅的内圆应该比树的周长大一点,给大榕树成长的空间,据此选择。
【详解】18.84÷10=1.884(米)
1.884÷3.14=0.6(米)=60(厘米)
A.直径小于大榕树直径,安装不上,排除;
B.直径刚好等于大榕树直径,没有留出一定距离,排除;
C.直径大于大榕树直径一些,可以;
D.直径大于大榕树直径太多,不合适,排除。
应选购内圆直径1米,外圆直径1.8米种座椅。
故答案为:C
【点睛】关键是掌握并灵活运用圆的周长公式。
9.20.56
【分析】根据半圆的周长=圆周长的一半+两条半径,圆的周长=,代入求解即可。
【详解】2×3.14×4÷2+2×4
=6.28×4÷2+2×4
=25.12÷2+8
=12.56+8
=20.56(厘米)
即它的周长是20.56厘米。
【点睛】本题考查半圆的周长,注意加上2条半径。
10.2
【分析】根据圆的周长==,假设小圆半径是1,则大圆直径是4,分别求出周长即可解答。
【详解】假设小圆半径是1,则大圆直径是4
2×3.14×1
=6.28×1
=6.28
4×3.14=12.56
12.56÷6.28=2
即大圆周长是小圆周长的2倍。
【点睛】本题考查圆的周长,公式要重点掌握。
11.8
【分析】根据正方形边长计算公式“C=4a”即可求出这根铁丝的长度,再把这根铁丝围成一个圆时,即已知周长,根据圆周长计算公式“C=πd”求出围成的圆的直径即可。
【详解】6.28×4=25.12(米)
25.12÷3.14=8(米)
这个圆的直径是8米。
【点睛】解答此题的关键一是弄清题意;二是正方形周长、圆周长计算公式的灵活运用。
12.9.42×3=28.26(平方厘米)
【分析】第一步求的是圆的周长,将圆拼成一个长方形,这个时候长方形的长等于圆周长的一半,长方形的宽等于半径,圆的面积等于长方形的面积,第二步求的是圆周长的一半,也就是长方形的长,第三步求面积,长×宽=面积,据此解答即可。
【详解】由分析可得:
第一步求圆的周长:2×3.14×3=18.84(厘米)
第二步求圆的周长的一半:18.84÷2=9.42(厘米)
第三步求面积:9.42×3=28.26(平方厘米)
【点睛】考查圆的面积推导过程,重点是能够知道圆的周长一半等于长方形的长,圆的半径等于长方形的宽。
13.9.42
【分析】把圆转化成近似的长方形,所以这个长方形的面积就等于圆的面积,,据此解答。
【详解】(1-)×3.14×
=
=9.42(平方厘米)
所以阴影部分的面积是9.42平方厘米。
【点睛】本题考查圆面积公式的灵活运用,转化思想是关键。
14.31.4平方厘米/31.4cm2
【分析】如下图:
在圆内画一个最大的正方形,以圆的直径为正方形的对角线;设圆的半径为r厘米,则这个图形中的正方形的面积为2r2平方厘米,已知这个正方形的面积是20平方厘米,用20÷2即可求出r2;然后根据圆面积公式:S=πr2,用3.14×(20÷2)即可求出圆面积。据此解答。
【详解】解:设圆的半径为r厘米,
2r2=20
2r2÷2=20÷2
r2=10
3.14×10=31.4(平方厘米)
这个圆的面积是31.4平方厘米。
【点睛】本题考查方外圆的面积计算,明确半径和正方形面积之间的关系是解答本题的关键。
15.×
【分析】在同圆或等圆中,所有的直径(或半径)都相等;如果不限定是什么样的圆,那么这句话是错的,据此解答。
【详解】在同圆或等圆中,所有的直径(或半径)都相等;在不等的圆中,所有的直径(或半径)都不相等,因此这句话是错的。
故答案为:×
16.×
【分析】我国魏晋时期数学家刘徽求得圆周率的近似值是3.14。我国南北朝科学家祖冲之算出圆周率大约在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后7位的人。
【详解】世界上第一个把圆周率的值精确到小数点后7位的科学家是祖冲之。即原题说法错误。
故答案为:×
17.×
【分析】由顶点在圆心的角的两边和这两边所截一段圆弧围成的图形,是扇形。据此概念分析解题即可。
【详解】这两条半径可能长度不相等,也可能长度相等,如果和这条弧对应的半径长度不相等。那么任意的两条半径可能和指定的一条弧没有关系。所以一条弧和两条半径不一定能组成扇形。
故答案为:×
【点睛】本题考查了扇形,掌握扇形的定义是解题的关键。
18.√
【分析】根据圆的周长公式:C=2πr,根据圆的面积公式:S=πr2,由于当半径相等,π是固定值,所以周长相等,也就是形状相同;半径相等,那么半径的平方也是相同,所以大小也是一样,据此即可判断。
【详解】由分析可知:
两个圆只要半径相等就可以说它的形状和大小完全一样,说法正确。
故答案为:√
【点睛】本题主要考查圆的周长和面积公式,熟练掌握它的公式并灵活运用。
19.×
【分析】圆周率是指圆的周长与它直径的比值,叫做圆周率,圆周率用字母“π”表示,圆周率是一个无限不循环小数,它的取值即3.1415926到3.1415927之间,π≈3.14,据此解答。
【详解】圆的周长÷直接≈3.14。
原题干说法错误。
故答案为:×
【点睛】明确圆周率的意义是解答本题的关键。
20.周长:37.7厘米;面积:20.75平方厘米
【分析】观察图形可知,阴影部分的面积=长方形的面积-直径是10厘米圆的面积的一半;阴影部分的周长=长方形的两条宽+长方形的一条长+直径是10厘米圆的周长的一半,根据圆的面积公式:S=πr2,圆的周长公式:C=πd,长方形的面积=长×宽,据此进行计算即可。
【详解】阴影部分的周长:
6×2+10+3.14×10÷2
=12+10+15.7
=22+15.7
=37.7(厘米)
阴影部分的面积:
10×6-3.14×(10÷2)2÷2
=60-3.14×25÷2
=60-39.25
=20.75(平方厘米)
21.29.76cm2
【分析】观察图形可知,阴影部分面积=上底是6cm,下底是14cm,高是8cm的梯形面积-半径是(8÷2)cm的圆的面积,根据梯形面积公式:面积=(上底+下底)×高÷2;圆的面积公式:面积=π×半径2;代入数据,即可解答。
【详解】(6+14)×8÷2-3.14×(8÷2)2
=20×8÷2-3.14×16
=160÷2-50.24
=80-50.24
=29.76(cm2)
22.16.42分米
【分析】因为长方形的长为6分米,而要求剪下的是最大的半圆,所以根据长方形内最大的半圆的半径特点可知:这个半圆的直径就等于长方形的长,半径为6÷2=3(分米),3分米<4分米,所以最大的半圆的直径为6分米,则半圆的周长根据圆的周长公式:C=πd,即可求解。
【详解】6÷2=3(分米)
3<4
3×3.14+3×2+1
=9.42+6+1
=15.42+1
=16.42(分米)
答:至少要买16.42分米的花边。
【点睛】解答此题的关键是明白:这个半圆的直径是6分米。
23.157盆
【分析】在封闭线路上植树,棵数与段数相等,即:棵数=间隔数。圆形广场就是封闭图形,有几个4米,就摆几盆花。根据圆的周长=,求出圆的周长即可解答。
【详解】3.14×200÷4
=628÷4
=157(盆)
答:一共需要摆157盆花。
【点睛】本题考查圆的周长,公式要重点掌握。
24.24.56分米
【分析】如图所示,这种捆扎方式所用绳子的长度刚好是1个圆的周长加上3条直径的长,根据圆的周长=πd,代入数值计算即可解答。
【详解】3.14×2×2+2×2×3
=3.14×4+4×3
=12.56+12
=24.56(分米)
答:这种捆扎方式所用绳子的长度是24.56分米。
【点睛】解答本题的关键是观察分析圆柱钢管放置的特征,再结合圆的周长计算公式来求解。
25.(1)
【分析】(1)用每步的长度乘步数,即可求出总长度,即为圆的周长,根据圆环的植树问题可知,棵数=间隔数,用总长度除以间隔的长度,即可解答;
(2)根据“圆的周长公式:”,求出圆的半径,再根据“圆的面积公式:”代入数值,即可求出这个花圃的占地面积。
【详解】(1)314×0.6÷1.2
=188.4÷1.2
=157(棵)
答:一共要栽157棵。
(2)314×0.6÷3.14÷2
=188.4÷3.14÷2
=60÷2
=30(米)
3.14×302
=3.14×900
=2826(平方米)
答:这个花圃的占地面积是2826平方米。
【点睛】本题考查植树问题的计算及圆的周长和面积公式的应用。理解题意,找出数量关系,列式计算即可。
26.942平方厘米
【分析】每个扇形的圆心角都是90°,那么每个这样的扇形的面积相当于半径是20厘米的圆面积的四分之一,根据圆的面积公式:,求出圆的面积再除以4即可计算出一层的面积,再乘3即可。
【详解】3.14×202÷4×3
=3.14×400÷4×3
=1256÷4×3
=314×3
=942(平方厘米)
答:这个角柜可以放置物品的面积是942平方厘米。
【点睛】此题主要考查圆的面积公式的灵活运用,关键是熟记公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
