(期末必刷好题)第5单元解决问题的策略检测卷2023-2024学年数学四年级下册苏教版(含答案)
文档属性
| 名称 | (期末必刷好题)第5单元解决问题的策略检测卷2023-2024学年数学四年级下册苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 361.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 21:07:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
(期末必刷好题)第5单元解决问题的策略检测卷2023-2024学年数学四年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
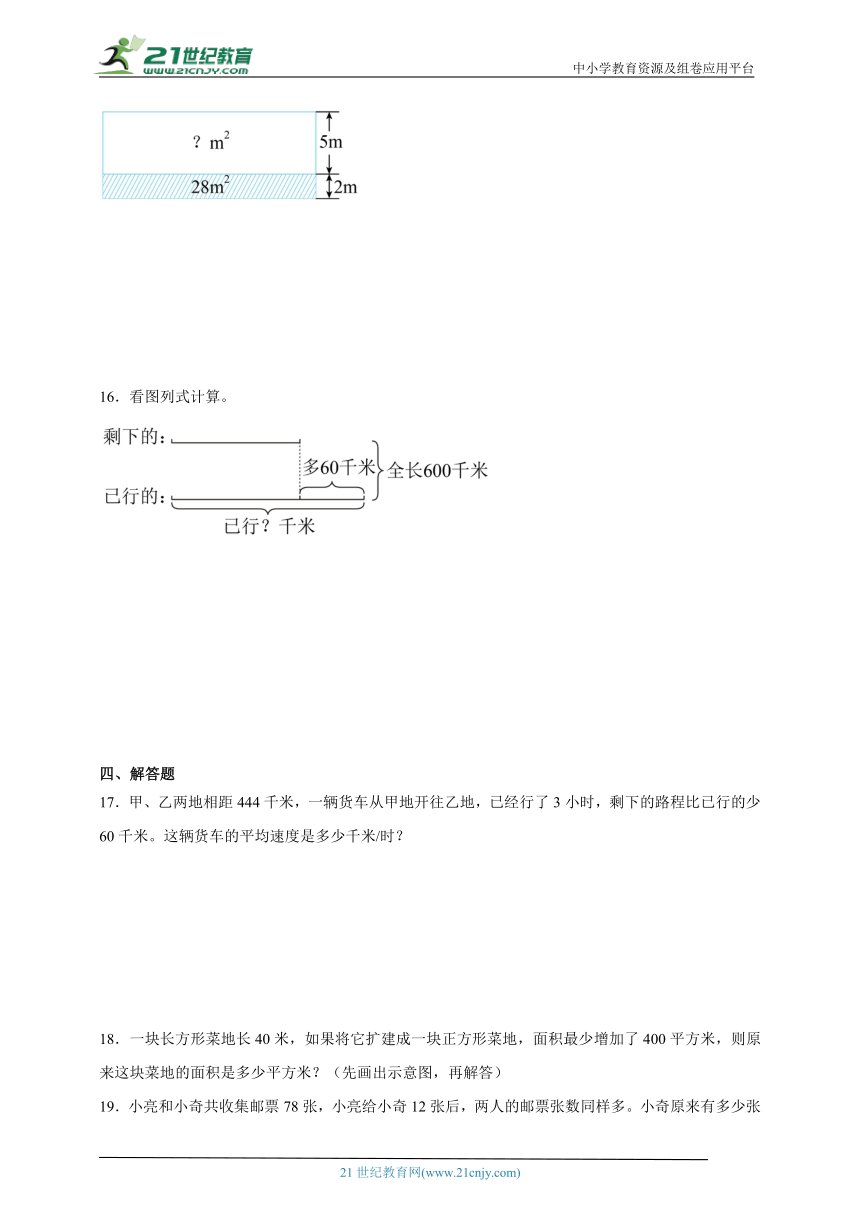
1.小羽和小彤去文具店买同样的笔记本,小羽买了5本,小彤买了8本,____________。笔记本的单价是多少元?选择下面( )条件不能解决这个问题。
A.小羽比小彤少花21元 B.小彤用去56元
C.他们一共用去91元 D.他们各自带了80元
2.甲、乙两个长方形完全相同,甲长方形的长减少6米,宽不变:乙长方形的宽减少6米,长不变。变化后甲、乙两个长方形剩下的面积相比,( )。
A.甲剩下的面积大 B.乙剩下的面积大 C.一样大 D.无法比较
3.学校运动会上,四年级同学组成3个表演方阵,每个方阵6行,每行6人。最外面一圈的学生穿红色表演服,其余学生穿黄色表演服,穿红色表演服的有( )人。
A.108 B.72 C.48 D.60
4.张阿姨买一套衣服用了88元,上衣比裤子贵12元,上衣( )元。
A.50 B.38 C.76 D.100
5.把一些长20厘米、宽16厘米的长方形纸片按下图所示的方法摆一摆,摆10层后形成的图形的周长是( )厘米。
A.360 B.720 C.1080 D.520
6.一个边长12米的正方形池塘周围有一条宽2米的小路,小路的面积是( )平方米。
A.52 B.112 C.88 D.100
7.如图所示,A点是甲乙两地的中点。一辆汽车从甲地开往乙地,已经行了3小时,这辆汽车的平均速度是( )千米/时。
A.70 B.80 C.155 D.145
8.姐姐和弟弟共写了86个大字,弟弟比姐姐少写14个。弟弟写了( )个。
A.29 B.36 C.50 D.57
二、填空题
9.学校健美操队排成一个8×8的方阵(每排8人,有8排),给最外面一圈的同学每人发一束花,一共要发( )束。
10.垃圾混放是垃圾,垃圾分类是资源。据研究表明每1千克的厨余垃圾经过处理大约能转化为200克有机肥。下表记录了小雨家一个月(4周)中分类出的厨余垃圾情况,这个月她们家的厨余垃圾大约能转化为( )千克的有机肥。
时间 第1周 第2周 第3周 第4周
厨余垃圾的质量/千克 14 17 18 16
11.果园里桃树和李树一共有305棵,李树比桃树少45棵,果园里桃树有( )棵,李树有( )棵。
12.已知图中大正方形的边长是10厘米,阴影部分的面积是( )平方厘米。
13.小红和小丽一共有46本课外书,小红比小丽多6本,小红有( )本课外书,小丽有( )本课外书。
14.包装240瓶墨水,每6瓶装一盒,10盒装一箱。如果先算240÷6,求的是( );如果先算10×6,求的是( )。
三、计算题
15.看图列式计算。
16.看图列式计算。
四、解答题
17.甲、乙两地相距444千米,一辆货车从甲地开往乙地,已经行了3小时,剩下的路程比已行的少60千米。这辆货车的平均速度是多少千米/时?
18.一块长方形菜地长40米,如果将它扩建成一块正方形菜地,面积最少增加了400平方米,则原来这块菜地的面积是多少平方米?(先画出示意图,再解答)
19.小亮和小奇共收集邮票78张,小亮给小奇12张后,两人的邮票张数同样多。小奇原来有多少张邮票?(先画线段图,再解答。)
20.甲、乙两地相距525千米,一辆汽车从甲地开往乙地,已经行了3小时,剩下的路程比已经行的少15千米。这辆汽车平均每小时行多少千米?
21.小兔白白和小猫咪咪同时从同一地点出发,白白向东走,速度是80米/分,咪咪向西走,速度是120米/分。经过5分钟,它们相距多少米?(先画图整理,再用两种方法解答)
参考答案:
1.D
【分析】单价=总价÷数量,只要知道笔记本的总价和数量就可以求出笔记本的单价,据此即可解答。
【详解】A.小羽比小彤少买8-5=3本,小羽比小彤少花21元,用21除以3即等于笔记本的单价。
B.小彤买了8本,小彤用去56元,用56除以8即等于笔记本的单价。
C.他们一共用去91元,他们一共买了5+8=13本,用91除以13即等于笔记本的单价。
D.他们各自带了80元,并没有说买笔记本用了多少元,不知笔记本总价,所以不能求出笔记本的单价。
故答案为:D
【点睛】熟练掌握总价、单价和数量三者之间的关系是解答本题的关键。
2.A
【分析】先表示出原来长方形的面积,再表示出减少的面积,原来的面积减减少的面积即可得剩下的面积,因甲乙两个长方形完全相同,所以哪个减少的面积小,剩下的面积就大。
【详解】甲剩下的面积=长×宽-6×宽;
乙剩下的面积=长×宽-6×长;
6×宽<6×长,所以甲剩下的面积大。
故答案为:A
【点睛】长方形面积=长×宽,剩下的面积=原来的面积-减少的面积。
3.D
【分析】每行人数减1,再乘4等于方阵最外面一圈的人数,再乘方阵个数即可解答。
【详解】(6-1)×4×3
=5×4×3
=20×3
=60(人)
故答案为:D
【点睛】明确方阵最外面一圈的人数等于每行人数减1的差乘4是解答本题的关键。
4.A
【分析】可用和差问题公式“(和+差)÷2=大数,(和-差)÷2=小数”解答。
【详解】上衣:(88+12)÷2
=100÷2
=50(元)
故答案为:A
【点睛】分析题中数量之间的关系,根据数量之间的关系解决问题。
5.B
【分析】一层有一个长方形,周长是2个宽与2个长的和,即1个长方形的周长。两层有3个长方形,周长是4个宽与4个长的和,即2个长方形的周长。三层有6个长方形,周长是6个宽与6个长的和,即3个长方形的周长。据此可知,摆几层,周长就是几个长方形的周长。据此解答。
【详解】(20+16)×2×10
=36×2×10
=72×10
=720(厘米)
则摆10层后形成的图形的周长是720厘米。
故答案为:B
【点睛】本题先根据已知图形明确摆的层数与图形周长之间的关系,再根据这个关系解决问题。
6.B
【分析】先求出小路的边长,再求出小路四条边所包围的总面积,最后用总面积减去正方形池塘的面积就是小路的面积。
【详解】12+2+2=16(米)
16×16-12×12
=256-144
=112(平方米)
故答案为:B
【点睛】掌握正方形的面积公式,求出小路边长所包围的总面积是关键。
7.B
【分析】根据图意,要求汽车的平均速度,根据速度=路程÷时间,甲汽车行驶的路程为两地距离的一半多15千米,时间为3小时,代入数据计算即可解答。
【详解】450÷2+15
=225+15
=240(千米)
240÷3=80(千米/时)
【点睛】解决此题的关键是理解题意求出已行的路程,利用好路程、速度和时间三者间的关系。
8.B
【分析】根据题意:姐姐和弟弟共写了86个大字,弟弟和姐姐相差14个,根据和差公式:(和-差)÷2=小数,计算出弟弟写字的个数。
【详解】(86-14)÷2
=72÷2
=36(个)
故答案为:B
【点睛】此题考查了和差问题的公式:(和-差)÷2=小数,(和+差)÷2=大数。
9.28
【分析】每排有8人,给最外面一圈的同学每人发一束花,需要(8×4)束花,因为方阵四个角上同学重复计算了,如图中黑圆所示,要减去重复计算的4个同学,一共要发(8×4-4)束花。
【详解】8×4-4
=32-4
=28(束)
学校健美操队排成一个8×8的方阵(每排8人,有8排),给最外面一圈的同学每人发一束花,一共要发(28)束。
【点睛】画图整理已知条件,能使题目一目了然,是解决问题的好策略。
10.13
【分析】由题意可得,先算出4周的厨余垃圾,再算出转化成多少克的有机肥,最后根据1000克=1千克换算单位。
【详解】(14+17+18+16)×200
=(31+18+16)×200
=(49+16)×200
=65×200
=13000(克)
13000克=13千克
【点睛】解决此题的关键在于明确质量单位进率:1000克=1千克。
11. 175 130
【分析】桃树和李树的总棵数是305棵,桃树和李树的棵数差是45棵,则数量较少的李树有(305-45)÷2棵。用总棵数减去李树的棵数,求出桃树的棵数。
【详解】(305-45)÷2
=260÷2
=130(棵)
130+45=175(棵)
果园里桃树有175棵,李树有130棵。
【点睛】本题考查和差问题,即已知大小两个数的和与它们的差,求大、小两个数的问题。小数=(和-差)÷2,大数=和-小数。
12.25
【分析】将图中阴影部分三角形平移可得到,阴影部分是正方形面积的,正方形面积=边长×边长,把数据代入计算出正方形面积,再除以4即是阴影部分面积。
【详解】10×10÷4
=100÷4
=25(平方厘米)
已知图中大正方形的边长是10厘米,阴影部分的面积是(25)平方厘米。
【点睛】用平移的方法可以巧妙地解决图形面积计算。
13. 26 20
【分析】由于小红比小丽多6本课外书,所以如果增加6本,则总数为小红的两倍,即小红有课外书(46+6)÷2=26(本);小丽比小红少6本,即小丽有课外书26-6=20(本)。
【详解】(46+6)÷2
=52÷2
=26(本)
26-6=20(本)
小红和小丽一共有46本课外书,小红比小丽多6本,小红有26本课外书,小丽有20本课外书。
【点睛】本题考查和差问题,灵活运用和差公式是解题关键。
已知两数的和及它们的差:
先求大数
大数=(和+差)÷2
小数=和-大数或小数=大数-差
先求小数
小数=(和-差)÷2
大数=和-小数或大数=小数+差
14. 可以装的盒数 一箱装的瓶数
【分析】包装240瓶墨水,每6瓶装一盒,所以240÷6求的是可以装的盒数;每6瓶装一盒,10盒装一箱,所以10×6求的是一箱有多少瓶。
【详解】根据分析可知,包装240瓶墨水,每6瓶装一盒,10盒装一箱。如果先算240÷6,求的是可以装的盒数;如果先算10×6,求的是一箱装的瓶数。。
【点睛】本题主要考查学生的综合分析能力。
15.70平方米
【分析】根据长方形的面积÷宽=长,用28除以2,计算出这个长方形的长是多少米,再根据长方形的面积=长×宽,用这个长方形的长乘空白部分的宽(5米),即可算出这个图形空白部分的面积是多少平方米。据此解答。
【详解】28÷2×5
=14×5
=70(平方米)
这个图形空白部分的面积是70平方米。
16.330千米
【分析】根据题意,已经行驶的路程=剩下的路程+60千米;其中,剩下的路程=(总路程-60千米)÷2。
【详解】(600-60)÷2+60
=540÷2+60
=270+60
=330(千米)
故已经行了330千米。
17.84千米/时
【分析】
首先,我们知道甲、乙两地相距444千米。货车已经行驶了3小时,剩下的路程比已经行驶的路程少了60千米。这意味着,如果我们将剩下的路程加上60千米,那么剩下的路程和已经行驶的路程就会相等。因此,我们可以将444千米分成两段相等的路程,每段长度为:(444+60)÷2=252千米,其中,252千米是货车已经行驶的路程,接下来,我们计算货车的平均速度。平均速度等于行驶的路程除以行驶的时间,所以货车的平均速度为:252÷3=84千米/时。
【详解】
(444+60)÷2÷3
=504÷2÷3
=252÷3
=84(千米/时)
答:这辆货车的平均速度是84千米/时。
18.1200平方米;示意图见详解
【分析】
将长方形扩建为正方形以后,正方形的边长为40米,面积最少增加了400平方米,根据长方形的面积=长×宽,用400除以40,即可求出增加的宽,然后再用40减去增加的宽,即为原来长方形菜地的宽;原来这块菜地的面积=原来长方形菜地的长×原来长方形菜地的宽,据此作答。
【详解】
根据上述分析,示意图如下:
原来长方形菜地的宽:
40-400÷40
=40-10
=30(米)
原来长方形菜地的面积:
40×30=1200(平方米)
答:原来这块菜地的面积是1200平方米。
19.27张;图见详解
【分析】小亮给小奇12张后,两人邮票的张数同样多,说明小亮比小奇多(12×2)张,小奇邮票的数量=(两人邮票数量和-两人邮票数量差)÷2,代入数据计算即可求出小奇邮票张数。
【详解】
(78-12×2)÷2
=(78-24)÷2
=54÷2
=27(张)
答:小奇原来有27张邮票。
20.90千米
【分析】甲、乙两相距525千米,剩下的路程比已经行的少15千米,所以525加15等于已经行的路程的2倍,再除以2即等于已经行了的路程,然后除以行驶的时间,即等于这辆汽车平均每小时行的路程,据此即可解答。
【详解】(525+15)÷2÷3
=540÷2÷3
=270÷3
=90(千米)
答:这辆汽车平均每小时行90千米。
21.1000米
【分析】根据题意可知,两只小兔向相反方向走,则两人的距离就等于两人的路程和。根据路程=速度×时间,分别求出两个的路程,再相加。也可以先求出两人速度和,再用速度和乘时间,求出总路程。
【详解】
方法一:80×5+120×5
=400+600
=1000(米)
方法二:(80+120)×5
=200×5
=1000(米)
答:它们相距1000米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
(期末必刷好题)第5单元解决问题的策略检测卷2023-2024学年数学四年级下册苏教版
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.小羽和小彤去文具店买同样的笔记本,小羽买了5本,小彤买了8本,____________。笔记本的单价是多少元?选择下面( )条件不能解决这个问题。
A.小羽比小彤少花21元 B.小彤用去56元
C.他们一共用去91元 D.他们各自带了80元
2.甲、乙两个长方形完全相同,甲长方形的长减少6米,宽不变:乙长方形的宽减少6米,长不变。变化后甲、乙两个长方形剩下的面积相比,( )。
A.甲剩下的面积大 B.乙剩下的面积大 C.一样大 D.无法比较
3.学校运动会上,四年级同学组成3个表演方阵,每个方阵6行,每行6人。最外面一圈的学生穿红色表演服,其余学生穿黄色表演服,穿红色表演服的有( )人。
A.108 B.72 C.48 D.60
4.张阿姨买一套衣服用了88元,上衣比裤子贵12元,上衣( )元。
A.50 B.38 C.76 D.100
5.把一些长20厘米、宽16厘米的长方形纸片按下图所示的方法摆一摆,摆10层后形成的图形的周长是( )厘米。
A.360 B.720 C.1080 D.520
6.一个边长12米的正方形池塘周围有一条宽2米的小路,小路的面积是( )平方米。
A.52 B.112 C.88 D.100
7.如图所示,A点是甲乙两地的中点。一辆汽车从甲地开往乙地,已经行了3小时,这辆汽车的平均速度是( )千米/时。
A.70 B.80 C.155 D.145
8.姐姐和弟弟共写了86个大字,弟弟比姐姐少写14个。弟弟写了( )个。
A.29 B.36 C.50 D.57
二、填空题
9.学校健美操队排成一个8×8的方阵(每排8人,有8排),给最外面一圈的同学每人发一束花,一共要发( )束。
10.垃圾混放是垃圾,垃圾分类是资源。据研究表明每1千克的厨余垃圾经过处理大约能转化为200克有机肥。下表记录了小雨家一个月(4周)中分类出的厨余垃圾情况,这个月她们家的厨余垃圾大约能转化为( )千克的有机肥。
时间 第1周 第2周 第3周 第4周
厨余垃圾的质量/千克 14 17 18 16
11.果园里桃树和李树一共有305棵,李树比桃树少45棵,果园里桃树有( )棵,李树有( )棵。
12.已知图中大正方形的边长是10厘米,阴影部分的面积是( )平方厘米。
13.小红和小丽一共有46本课外书,小红比小丽多6本,小红有( )本课外书,小丽有( )本课外书。
14.包装240瓶墨水,每6瓶装一盒,10盒装一箱。如果先算240÷6,求的是( );如果先算10×6,求的是( )。
三、计算题
15.看图列式计算。
16.看图列式计算。
四、解答题
17.甲、乙两地相距444千米,一辆货车从甲地开往乙地,已经行了3小时,剩下的路程比已行的少60千米。这辆货车的平均速度是多少千米/时?
18.一块长方形菜地长40米,如果将它扩建成一块正方形菜地,面积最少增加了400平方米,则原来这块菜地的面积是多少平方米?(先画出示意图,再解答)
19.小亮和小奇共收集邮票78张,小亮给小奇12张后,两人的邮票张数同样多。小奇原来有多少张邮票?(先画线段图,再解答。)
20.甲、乙两地相距525千米,一辆汽车从甲地开往乙地,已经行了3小时,剩下的路程比已经行的少15千米。这辆汽车平均每小时行多少千米?
21.小兔白白和小猫咪咪同时从同一地点出发,白白向东走,速度是80米/分,咪咪向西走,速度是120米/分。经过5分钟,它们相距多少米?(先画图整理,再用两种方法解答)
参考答案:
1.D
【分析】单价=总价÷数量,只要知道笔记本的总价和数量就可以求出笔记本的单价,据此即可解答。
【详解】A.小羽比小彤少买8-5=3本,小羽比小彤少花21元,用21除以3即等于笔记本的单价。
B.小彤买了8本,小彤用去56元,用56除以8即等于笔记本的单价。
C.他们一共用去91元,他们一共买了5+8=13本,用91除以13即等于笔记本的单价。
D.他们各自带了80元,并没有说买笔记本用了多少元,不知笔记本总价,所以不能求出笔记本的单价。
故答案为:D
【点睛】熟练掌握总价、单价和数量三者之间的关系是解答本题的关键。
2.A
【分析】先表示出原来长方形的面积,再表示出减少的面积,原来的面积减减少的面积即可得剩下的面积,因甲乙两个长方形完全相同,所以哪个减少的面积小,剩下的面积就大。
【详解】甲剩下的面积=长×宽-6×宽;
乙剩下的面积=长×宽-6×长;
6×宽<6×长,所以甲剩下的面积大。
故答案为:A
【点睛】长方形面积=长×宽,剩下的面积=原来的面积-减少的面积。
3.D
【分析】每行人数减1,再乘4等于方阵最外面一圈的人数,再乘方阵个数即可解答。
【详解】(6-1)×4×3
=5×4×3
=20×3
=60(人)
故答案为:D
【点睛】明确方阵最外面一圈的人数等于每行人数减1的差乘4是解答本题的关键。
4.A
【分析】可用和差问题公式“(和+差)÷2=大数,(和-差)÷2=小数”解答。
【详解】上衣:(88+12)÷2
=100÷2
=50(元)
故答案为:A
【点睛】分析题中数量之间的关系,根据数量之间的关系解决问题。
5.B
【分析】一层有一个长方形,周长是2个宽与2个长的和,即1个长方形的周长。两层有3个长方形,周长是4个宽与4个长的和,即2个长方形的周长。三层有6个长方形,周长是6个宽与6个长的和,即3个长方形的周长。据此可知,摆几层,周长就是几个长方形的周长。据此解答。
【详解】(20+16)×2×10
=36×2×10
=72×10
=720(厘米)
则摆10层后形成的图形的周长是720厘米。
故答案为:B
【点睛】本题先根据已知图形明确摆的层数与图形周长之间的关系,再根据这个关系解决问题。
6.B
【分析】先求出小路的边长,再求出小路四条边所包围的总面积,最后用总面积减去正方形池塘的面积就是小路的面积。
【详解】12+2+2=16(米)
16×16-12×12
=256-144
=112(平方米)
故答案为:B
【点睛】掌握正方形的面积公式,求出小路边长所包围的总面积是关键。
7.B
【分析】根据图意,要求汽车的平均速度,根据速度=路程÷时间,甲汽车行驶的路程为两地距离的一半多15千米,时间为3小时,代入数据计算即可解答。
【详解】450÷2+15
=225+15
=240(千米)
240÷3=80(千米/时)
【点睛】解决此题的关键是理解题意求出已行的路程,利用好路程、速度和时间三者间的关系。
8.B
【分析】根据题意:姐姐和弟弟共写了86个大字,弟弟和姐姐相差14个,根据和差公式:(和-差)÷2=小数,计算出弟弟写字的个数。
【详解】(86-14)÷2
=72÷2
=36(个)
故答案为:B
【点睛】此题考查了和差问题的公式:(和-差)÷2=小数,(和+差)÷2=大数。
9.28
【分析】每排有8人,给最外面一圈的同学每人发一束花,需要(8×4)束花,因为方阵四个角上同学重复计算了,如图中黑圆所示,要减去重复计算的4个同学,一共要发(8×4-4)束花。
【详解】8×4-4
=32-4
=28(束)
学校健美操队排成一个8×8的方阵(每排8人,有8排),给最外面一圈的同学每人发一束花,一共要发(28)束。
【点睛】画图整理已知条件,能使题目一目了然,是解决问题的好策略。
10.13
【分析】由题意可得,先算出4周的厨余垃圾,再算出转化成多少克的有机肥,最后根据1000克=1千克换算单位。
【详解】(14+17+18+16)×200
=(31+18+16)×200
=(49+16)×200
=65×200
=13000(克)
13000克=13千克
【点睛】解决此题的关键在于明确质量单位进率:1000克=1千克。
11. 175 130
【分析】桃树和李树的总棵数是305棵,桃树和李树的棵数差是45棵,则数量较少的李树有(305-45)÷2棵。用总棵数减去李树的棵数,求出桃树的棵数。
【详解】(305-45)÷2
=260÷2
=130(棵)
130+45=175(棵)
果园里桃树有175棵,李树有130棵。
【点睛】本题考查和差问题,即已知大小两个数的和与它们的差,求大、小两个数的问题。小数=(和-差)÷2,大数=和-小数。
12.25
【分析】将图中阴影部分三角形平移可得到,阴影部分是正方形面积的,正方形面积=边长×边长,把数据代入计算出正方形面积,再除以4即是阴影部分面积。
【详解】10×10÷4
=100÷4
=25(平方厘米)
已知图中大正方形的边长是10厘米,阴影部分的面积是(25)平方厘米。
【点睛】用平移的方法可以巧妙地解决图形面积计算。
13. 26 20
【分析】由于小红比小丽多6本课外书,所以如果增加6本,则总数为小红的两倍,即小红有课外书(46+6)÷2=26(本);小丽比小红少6本,即小丽有课外书26-6=20(本)。
【详解】(46+6)÷2
=52÷2
=26(本)
26-6=20(本)
小红和小丽一共有46本课外书,小红比小丽多6本,小红有26本课外书,小丽有20本课外书。
【点睛】本题考查和差问题,灵活运用和差公式是解题关键。
已知两数的和及它们的差:
先求大数
大数=(和+差)÷2
小数=和-大数或小数=大数-差
先求小数
小数=(和-差)÷2
大数=和-小数或大数=小数+差
14. 可以装的盒数 一箱装的瓶数
【分析】包装240瓶墨水,每6瓶装一盒,所以240÷6求的是可以装的盒数;每6瓶装一盒,10盒装一箱,所以10×6求的是一箱有多少瓶。
【详解】根据分析可知,包装240瓶墨水,每6瓶装一盒,10盒装一箱。如果先算240÷6,求的是可以装的盒数;如果先算10×6,求的是一箱装的瓶数。。
【点睛】本题主要考查学生的综合分析能力。
15.70平方米
【分析】根据长方形的面积÷宽=长,用28除以2,计算出这个长方形的长是多少米,再根据长方形的面积=长×宽,用这个长方形的长乘空白部分的宽(5米),即可算出这个图形空白部分的面积是多少平方米。据此解答。
【详解】28÷2×5
=14×5
=70(平方米)
这个图形空白部分的面积是70平方米。
16.330千米
【分析】根据题意,已经行驶的路程=剩下的路程+60千米;其中,剩下的路程=(总路程-60千米)÷2。
【详解】(600-60)÷2+60
=540÷2+60
=270+60
=330(千米)
故已经行了330千米。
17.84千米/时
【分析】
首先,我们知道甲、乙两地相距444千米。货车已经行驶了3小时,剩下的路程比已经行驶的路程少了60千米。这意味着,如果我们将剩下的路程加上60千米,那么剩下的路程和已经行驶的路程就会相等。因此,我们可以将444千米分成两段相等的路程,每段长度为:(444+60)÷2=252千米,其中,252千米是货车已经行驶的路程,接下来,我们计算货车的平均速度。平均速度等于行驶的路程除以行驶的时间,所以货车的平均速度为:252÷3=84千米/时。
【详解】
(444+60)÷2÷3
=504÷2÷3
=252÷3
=84(千米/时)
答:这辆货车的平均速度是84千米/时。
18.1200平方米;示意图见详解
【分析】
将长方形扩建为正方形以后,正方形的边长为40米,面积最少增加了400平方米,根据长方形的面积=长×宽,用400除以40,即可求出增加的宽,然后再用40减去增加的宽,即为原来长方形菜地的宽;原来这块菜地的面积=原来长方形菜地的长×原来长方形菜地的宽,据此作答。
【详解】
根据上述分析,示意图如下:
原来长方形菜地的宽:
40-400÷40
=40-10
=30(米)
原来长方形菜地的面积:
40×30=1200(平方米)
答:原来这块菜地的面积是1200平方米。
19.27张;图见详解
【分析】小亮给小奇12张后,两人邮票的张数同样多,说明小亮比小奇多(12×2)张,小奇邮票的数量=(两人邮票数量和-两人邮票数量差)÷2,代入数据计算即可求出小奇邮票张数。
【详解】
(78-12×2)÷2
=(78-24)÷2
=54÷2
=27(张)
答:小奇原来有27张邮票。
20.90千米
【分析】甲、乙两相距525千米,剩下的路程比已经行的少15千米,所以525加15等于已经行的路程的2倍,再除以2即等于已经行了的路程,然后除以行驶的时间,即等于这辆汽车平均每小时行的路程,据此即可解答。
【详解】(525+15)÷2÷3
=540÷2÷3
=270÷3
=90(千米)
答:这辆汽车平均每小时行90千米。
21.1000米
【分析】根据题意可知,两只小兔向相反方向走,则两人的距离就等于两人的路程和。根据路程=速度×时间,分别求出两个的路程,再相加。也可以先求出两人速度和,再用速度和乘时间,求出总路程。
【详解】
方法一:80×5+120×5
=400+600
=1000(米)
方法二:(80+120)×5
=200×5
=1000(米)
答:它们相距1000米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
