新疆生产建设兵团第六师奇台农场中学(人教版)高中数学必修4教学设计:2-4-1平面向量数量积的物理背景及其含义
文档属性
| 名称 | 新疆生产建设兵团第六师奇台农场中学(人教版)高中数学必修4教学设计:2-4-1平面向量数量积的物理背景及其含义 |  | |
| 格式 | zip | ||
| 文件大小 | 57.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-08 21:59:25 | ||
图片预览

文档简介
2.4.1平面向量数量积的物理背景及其含义(教学设计)
一、教学目标
1.知识与技能目标
理解平面向量的数量积的定义及几何意义;熟练掌握平面向量数量积的性质;掌握关于平面向量数量积的几类重要题型.
2.过程与能力目标
通过对数量积的定义及运算性质的应用,加深学生对知识的理解与掌握,同时,通过对数量积的几类重要问题的解答,培养学生的归纳能力,运算能力,应用所学知识解决问题的能力.
3.情感与态度目标
通过本节课的学习,激发学生学习数学的兴趣和善于发现、勇于探索的精神,体会学习的快乐.体会各学科之间是密不可分的.培养学生思考问题认真严谨的学习态度.
二、教学重、难点
1.教学重点
平面向量的数量积的定义、几何意义及其性质.
2.教学难点
平面向量数量积的定义及运算性质的理解和平面向量数量积的应用.
三、教学准备
多媒体、彩色粉笔
四、教学过程新课
(一)创设情景,引入新课
问题:如图所示,一辆小车,在力F的作用下,
产生位移S,那么请问力F在这个运动过程中所做的功?
(1)力F所做的功W:W=
(2)这个公式有什么特点?请完成下列填空:
W(功)是 量,F(力)是 量,S(位移)是 量,θ是 .
(3)你能用文字语言表述“功的计算公式”吗?
答:功是力与位移的大小及其夹角余弦的乘积.
思考:如果我们将公式中的力与位移推广到一般向量,能否把“功”看成这两个向量的一种运算的结果呢?
(二)探究新知
探究一:明晰向量数量积的定义
数量积的定义:
已知两个非零向量和,把数量叫做与数量积(或内积),记作
规定:零向量与任意向量的数量积都为零,即
注意: “”中间的“· ”不可以省略,也不可以用“ ”代替.
2、提出问题
(1)向量数量积是一个向量还是一个数量?
(2)影响数量积大小的因素有哪些?
(3)学生讨论完成下表
θ的范围
0°≤θ<90°
θ=90°
90°<θ≤180°
·的与0的关系
探究二:向量数量积的几何意义
给出“投影”定义
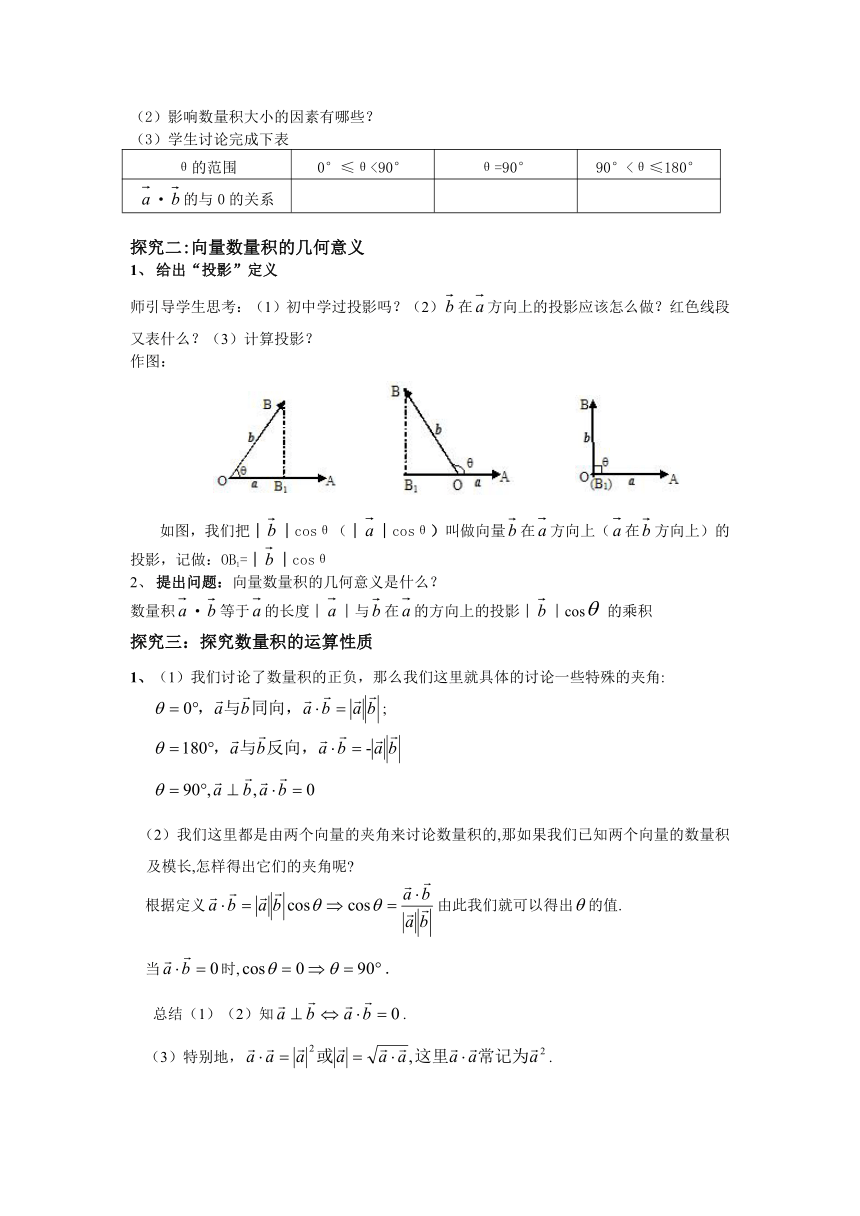
师引导学生思考:(1)初中学过投影吗?(2)在方向上的投影应该怎么做?红色线段又表什么?(3)计算投影?
作图:
如图,我们把││cosθ(││cosθ)叫做向量在方向上(在方向上)的投影,记做:OB1=││cosθ
提出问题:向量数量积的几何意义是什么?
数量积·等于的长度︱︱与在的方向上的投影︱︱cos 的乘积
探究三:探究数量积的运算性质
1、(1)我们讨论了数量积的正负,那么我们这里就具体的讨论一些特殊的夹角:
;
(2)我们这里都是由两个向量的夹角来讨论数量积的,那如果我们已知两个向量的数量积及模长,怎样得出它们的夹角呢?
根据定义由此我们就可以得出的值.
当时,.
总结(1)(2)知.
(3)特别地,.
(4)请判断.
分析: ,
.
这些就是数量积的性质.在课堂上以上性质以探究形式出现,让同学们积极思考,踊跃回答并总结其各自的应用。
2、小结数量积的性质
性质:若和均为非零向量
(1)⊥·=0 (垂直)
(2)与同向时,· =︱︱·︱︱,
与反向 时,· =-︱︱·︱︱
特别地:·=︱︱2 ,= (长度)
(3)cosθ=(夹角)
(4)︱·︱ ≤︱︱·︱︱(注意等号成立的条件)
(三)巩固新知
例1已知,的夹角=120°,求.
解:根据数量积的定义:
=
=5
=-10.
例2已知求与的夹角.
注意:例2中强调θ的取值范围
例3已知△ABC中,=, =,当· <0或·=0时,试判断
△ABC的形状.
∴ΔABC是钝角三角形
∴ΔABC是直角三角形
(四)巩固练习
1、在△ABC中BC=8,CA=7,求
2、︱︱=4,与的夹角为30°,求在方向上的投影
(五)归纳小结
(1)平面向量的数量积;
(2)平面向量的数量积的几何意义;
(3)平面向量数量积的重要性质
(六)布置作业
课本:习题2.4 第1、2、3题
一、教学目标
1.知识与技能目标
理解平面向量的数量积的定义及几何意义;熟练掌握平面向量数量积的性质;掌握关于平面向量数量积的几类重要题型.
2.过程与能力目标
通过对数量积的定义及运算性质的应用,加深学生对知识的理解与掌握,同时,通过对数量积的几类重要问题的解答,培养学生的归纳能力,运算能力,应用所学知识解决问题的能力.
3.情感与态度目标
通过本节课的学习,激发学生学习数学的兴趣和善于发现、勇于探索的精神,体会学习的快乐.体会各学科之间是密不可分的.培养学生思考问题认真严谨的学习态度.
二、教学重、难点
1.教学重点
平面向量的数量积的定义、几何意义及其性质.
2.教学难点
平面向量数量积的定义及运算性质的理解和平面向量数量积的应用.
三、教学准备
多媒体、彩色粉笔
四、教学过程新课
(一)创设情景,引入新课
问题:如图所示,一辆小车,在力F的作用下,
产生位移S,那么请问力F在这个运动过程中所做的功?
(1)力F所做的功W:W=
(2)这个公式有什么特点?请完成下列填空:
W(功)是 量,F(力)是 量,S(位移)是 量,θ是 .
(3)你能用文字语言表述“功的计算公式”吗?
答:功是力与位移的大小及其夹角余弦的乘积.
思考:如果我们将公式中的力与位移推广到一般向量,能否把“功”看成这两个向量的一种运算的结果呢?
(二)探究新知
探究一:明晰向量数量积的定义
数量积的定义:
已知两个非零向量和,把数量叫做与数量积(或内积),记作
规定:零向量与任意向量的数量积都为零,即
注意: “”中间的“· ”不可以省略,也不可以用“ ”代替.
2、提出问题
(1)向量数量积是一个向量还是一个数量?
(2)影响数量积大小的因素有哪些?
(3)学生讨论完成下表
θ的范围
0°≤θ<90°
θ=90°
90°<θ≤180°
·的与0的关系
探究二:向量数量积的几何意义
给出“投影”定义
师引导学生思考:(1)初中学过投影吗?(2)在方向上的投影应该怎么做?红色线段又表什么?(3)计算投影?
作图:
如图,我们把││cosθ(││cosθ)叫做向量在方向上(在方向上)的投影,记做:OB1=││cosθ
提出问题:向量数量积的几何意义是什么?
数量积·等于的长度︱︱与在的方向上的投影︱︱cos 的乘积
探究三:探究数量积的运算性质
1、(1)我们讨论了数量积的正负,那么我们这里就具体的讨论一些特殊的夹角:
;
(2)我们这里都是由两个向量的夹角来讨论数量积的,那如果我们已知两个向量的数量积及模长,怎样得出它们的夹角呢?
根据定义由此我们就可以得出的值.
当时,.
总结(1)(2)知.
(3)特别地,.
(4)请判断.
分析: ,
.
这些就是数量积的性质.在课堂上以上性质以探究形式出现,让同学们积极思考,踊跃回答并总结其各自的应用。
2、小结数量积的性质
性质:若和均为非零向量
(1)⊥·=0 (垂直)
(2)与同向时,· =︱︱·︱︱,
与反向 时,· =-︱︱·︱︱
特别地:·=︱︱2 ,= (长度)
(3)cosθ=(夹角)
(4)︱·︱ ≤︱︱·︱︱(注意等号成立的条件)
(三)巩固新知
例1已知,的夹角=120°,求.
解:根据数量积的定义:
=
=5
=-10.
例2已知求与的夹角.
注意:例2中强调θ的取值范围
例3已知△ABC中,=, =,当· <0或·=0时,试判断
△ABC的形状.
∴ΔABC是钝角三角形
∴ΔABC是直角三角形
(四)巩固练习
1、在△ABC中BC=8,CA=7,求
2、︱︱=4,与的夹角为30°,求在方向上的投影
(五)归纳小结
(1)平面向量的数量积;
(2)平面向量的数量积的几何意义;
(3)平面向量数量积的重要性质
(六)布置作业
课本:习题2.4 第1、2、3题
