北师大版七年级数学下册第五章生活中的轴对称单元测试卷(含解析)
文档属性
| 名称 | 北师大版七年级数学下册第五章生活中的轴对称单元测试卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 533.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览


文档简介
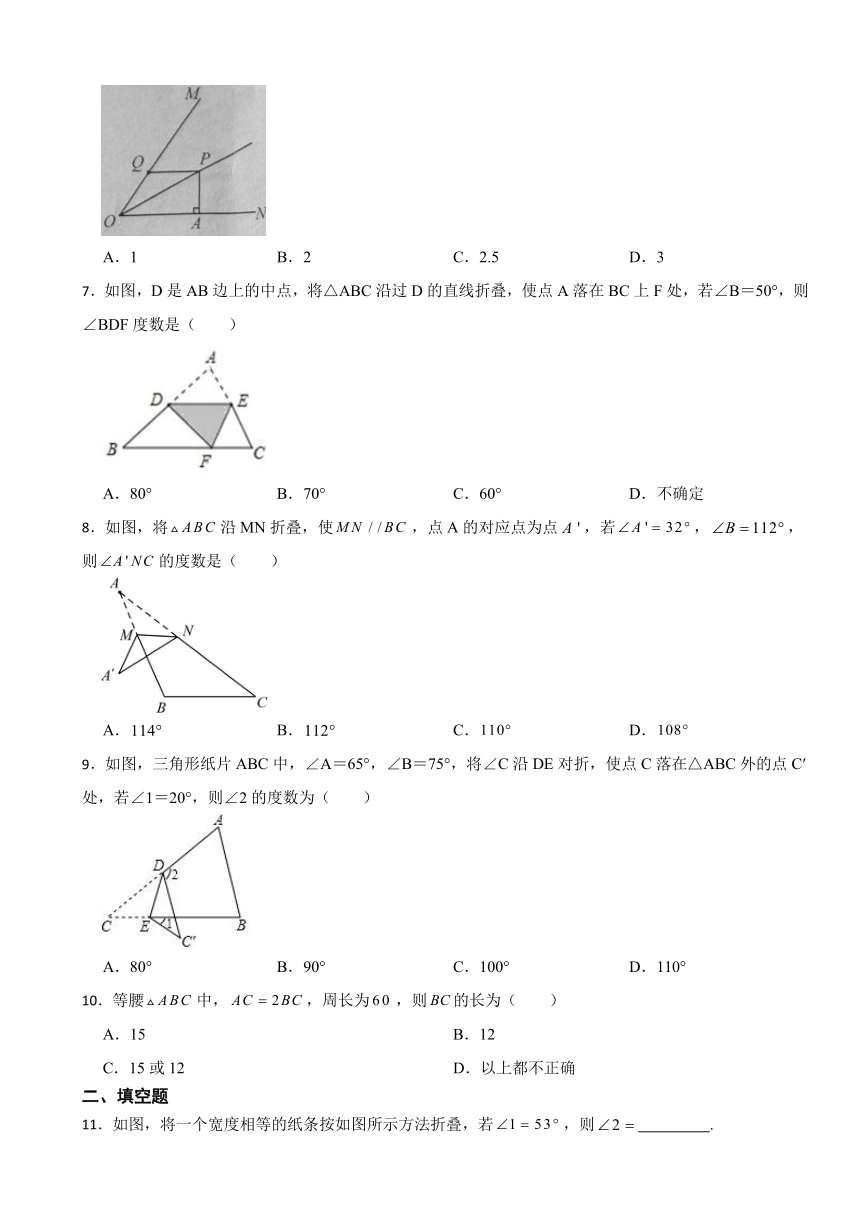
北师大版七年级数学下册第五章生活中的轴对称单元测试卷
一、单选题
1.下列运动图标中,属于轴对称图形的是( )
A. B. C. D.
2.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12 B.13 C.14 D.15
3.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
4.如图,将一张长方形纸片折叠,如果,则等于( )
A. B. C. D.
5.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
6.如图,平分,于点A,点Q是射线上的一个动点,若,则的最小值为( )
A.1 B.2 C.2.5 D.3
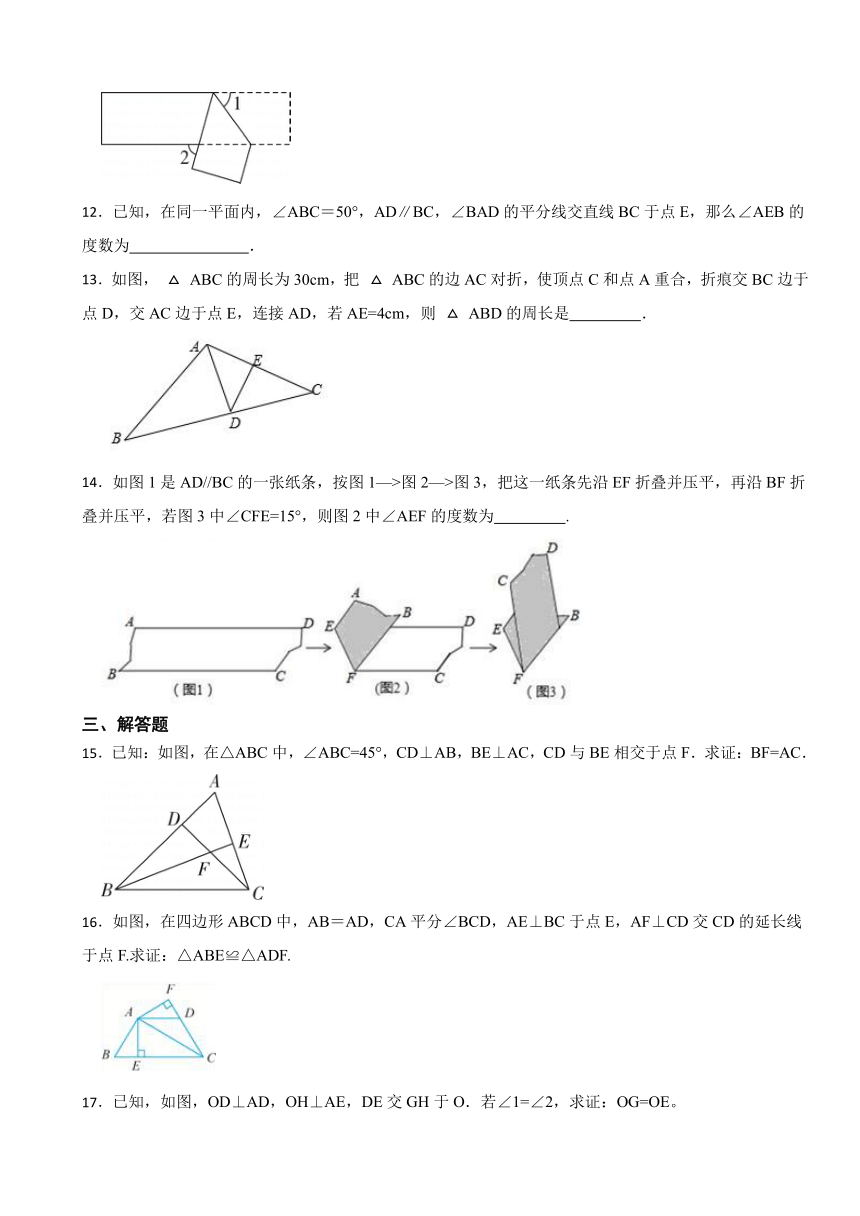
7.如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF度数是( )
A.80° B.70° C.60° D.不确定
8.如图,将沿MN折叠,使,点A的对应点为点,若,,则的度数是( )
A. B. C. D.
9.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( )
A.80° B.90° C.100° D.110°
10.等腰中,,周长为,则的长为( )
A.15 B.12
C.15或12 D.以上都不正确
二、填空题
11.如图,将一个宽度相等的纸条按如图所示方法折叠,若,则 .
12.已知,在同一平面内,∠ABC=50°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .
13.如图, ABC的周长为30cm,把 ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4cm,则 ABD的周长是 .
14.如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为 .
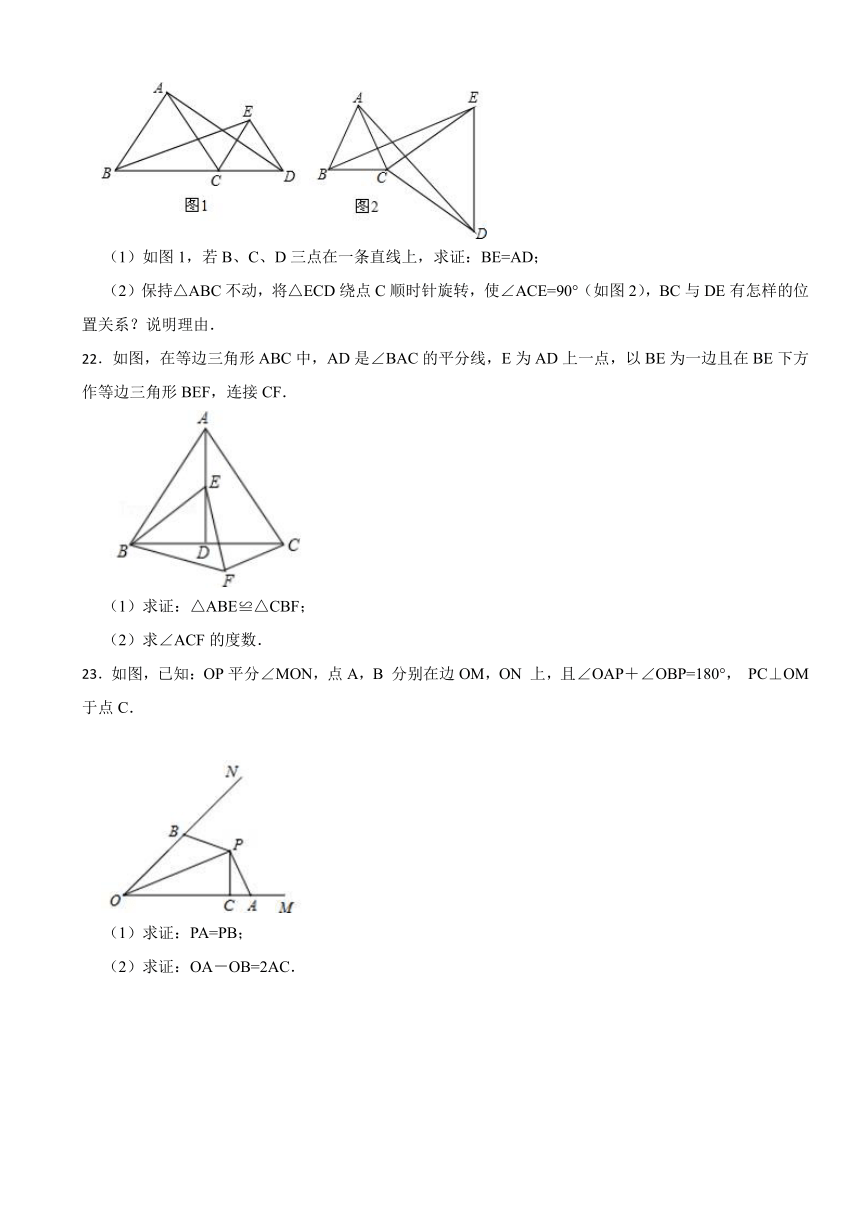
三、解答题
15.已知:如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,CD与BE相交于点F.求证:BF=AC.
16.如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.
17.已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE。
18.两个城镇、与两条公路,位置如图所示,其中是东西方向的公路.现电信部门需在处修建一座信号发射塔,要求发射塔到两个城镇、的距离必须相等,到两条公路,的距离也必须相等,且在的内部,请在图中,用尺规作图找出符合条件的点.(不写已知、求作、作法,只保留作图痕迹)
19.某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子。BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短
四、综合题
20.用一条长为20cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成一条边是5cm的等腰三角形吗?若能,求出其他两边;若不能,说明理由.
21.△ABC和△ECD都是等边三角形
(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
22.如图,在等边三角形ABC中,AD是∠BAC的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接CF.
(1)求证:△ABE≌△CBF;
(2)求∠ACF的度数.
23.如图,已知:OP平分∠MON,点A,B 分别在边OM,ON 上,且∠OAP+∠OBP=180°, PC⊥OM于点C.
(1)求证:PA=PB;
(2)求证:OA-OB=2AC.
答案解析部分
1.【答案】B
【解析】【解答】解:A、不是轴对称图形,此选项不符合题意;
B、是轴对称图形,此选项符合题意;
C、不是轴对称图形,此选项不符合题意;
D、不是轴对称图形,此选项不符合题意.
故答案为:B.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,据此一一判断得出答案.
2.【答案】A
【解析】【解答】解:∵D为BC的中点,且BC=6,
∴BD= BC=3,
由折叠性质知NA=ND,
则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,
故答案为:A.
【分析】由折叠性质知NA=ND,根据中点定义BD= BC=3,根据三角形的周长计算方法及等量代换即可得出答案。
3.【答案】D
【解析】【解答】解:A、此标志不是轴对称图形,故A不符合题意;
B、此标志不是轴对称图形,故B不符合题意;
C、此标志不是轴对称图形,故C不符合题意;
D、此标志是轴对称图形,故D符合题意;
故答案为:D
【分析】轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】C
【解析】【解答】解:如图:
∵AB∥CD,∠1=50°,∴∠CEH=∠1=50°,
∴∠HED=180°-∠CEH=180°-50°=130°,
由折叠得:∠HEF=∠FED=∠HED=65°,
∴∠α=∠FED=65°.
故选:C.
【分析】由平行线的性质可得∠CEH=∠1,由邻补角的定义可求得∠HED的度数,根据折叠的性质得∠HEF=∠FED=∠HED,然后根据平行线的性质可求解.
5.【答案】B
【解析】【解答】解:∵OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,
∴PC=PD,故A正确;
在Rt△OCP与Rt△ODP中,
,
∴△OCP≌△ODP,
∴∠CPO=∠DPO,OC=OD,故C、D正确.
不能得出∠CPD=∠DOP,故B错误.
故选B.
【分析】先根据角平分线的性质得出PC=PD,再利用HL证明△OCP≌△ODP,根据全等三角形的性质得出∠CPO=∠DPO,OC=OD.
6.【答案】D
【解析】【解答】解:由题意得当时将有最小值,
∵平分,于点A,,
∴,
故答案为:D
【分析】先根据题意得到当时将有最小值,进而根据角平分线的性质即可求解。
7.【答案】A
【解析】【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,∴AD=DF,∵D是AB边的中点,∴AD=BD,∴BD=DF,∴∠B=∠BFD,∵∠B=50°,∴∠BDF=180°-∠B-∠BFD=180°-50°-50°=80°,
故答案为:A.
【分析】根据点D是AB的中点结合翻折的性质可得到BD=DF,所以得到∠B=∠BFD,再利用三角形的内角和求解即可。
8.【答案】D
【解析】【解答】解:∵
∵,
,
由折叠的性质可知 ,
,
,
故答案为:D.
【分析】由平行线的性质可得∠MNC=180°-∠C=144°,由折叠可得 , ,结合三角形的内角和求出 ,从而求出 ,根据 即可求解.
9.【答案】C
【解析】【解答】解:∠A=65°,∠B=75°,∴∠C=∠C’=180°-∠A-∠B=40°,
由翻折变换的性质可得:∠DEC=∠DEC’,
∠DEC+∠DEB=∠DEC+∠DEC’-∠1=180°,
∴∠DEC=100°,
∴∠CDE=∠EDC’=180°-∠C-∠DEC=40°,
∴∠2=180°-∠CDE-∠EDC’=100°.
故答案为:C.
【分析】根据三角形的内角和定理及折叠的性质求出∠C=∠C’=180°-∠A-∠B=40°,∠DEC=∠DEC’,由图可知∠DEC+∠DEB=∠DEC+∠DEC’-∠1=180°,从中求出∠DEC=100°,进而可得∠CDE=∠EDC=40°,再根据平角的定义即可求出答案.
10.【答案】B
【解析】【解答】解:当时,,则;
当时,,但,故构不成三角形.
故答案为:B.
【分析】当AC=AB时,根据△ABC的周长为60可得BC的值;当BC=AB时,同理求出BC,然后结合三角形的三边关系进行判断.
11.【答案】74°
【解析】【解答】解:如图:
依题意得:AC∥DE,
∴∠2=∠CAD,
∵∠1=∠BAD=53°,
∴∠CAD=180°-(∠1+∠BAD)=74°,
∴∠2=74°.
故答案为:74°.
【分析】首先根据两直线平行,同位角相等可得∠2=∠CAD,再由翻折的性质可得∠1=∠BAD=53°,然后根据平角的定义可求出∠CAD=74°,据此可得出∠2的度数.
12.【答案】65°或25°
【解析】【解答】解:分情况讨论:(1)∵AE平分∠BAD,
∴∠EAD=∠EAB,
∵AD∥BC,
∴∠EAD=∠AEB,
∴∠BAD=∠AEB,
∵∠ABC=50°,
∴∠AEB= (180°-50°)=65°.(2)∵AE平分∠BAD,
∴∠EAD=∠EAB= ,
∵AD∥BC,
∴∠AEB=∠DAE= ,∠DAB=∠ABC,
∵∠ABC=50°,
∴∠AEB= ×50°=25°.
故答案为:65°或25°.
【分析】首先根据角平分线的定义得出∠EAD=∠EAB,再分情况讨论计算即可.
13.【答案】22cm
【解析】【解答】解:根据折叠方法可得AE=CE,AD=CD,
∵AE=4cm,
∴CE=4cm,
∵△ABC的周长为30cm,
∴AB+CB=30-8=22(cm),
△ABD的周长是:AB+BD+AD=AB+BC=22cm
【分析】由折叠的性质可得AE=CE=4cm,AD=CD,利用△ABC的周长求出AB+BC的长,从而求出△ABD的周长.
14.【答案】115°
【解析】【解答】解:如图,设∠B'FE=x,
当纸条沿EF折叠时,
∴∠BFE=∠B'FE=x,∠AEF=∠A'EF,
∴∠BFC=∠BFE-∠CFE=x-15°,
当纸条沿BF折叠时,
∴∠C'FB=∠CFB=x-15°,
∵∠B'FE+∠BFE+∠CFB=180°,
∴x+x+x-15°=180°,
解得x=65°,
∵A'D'∥B'C',
∴∠A'EF=180°-∠B'FE=180°-65°=115°,
∴∠AEF=115°.
故答案为:115°.
【分析】设∠B'FE=x,根据折叠的性质得∠BFE=∠B'FE=x,∠AEF=∠A'EF, 则∠BFC=x-15°, 再由两次折叠后得到∠CFB=∠BFC=x-15°,然后根据平角定义列方程求解,再根据平行线的性质得∠A'EF=180°-∠B'FE=115°,最后根据折叠的性质得出∠AEF=115°.
15.【答案】证明:CD⊥AB,BE⊥AC,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠ACD+∠EFC=90°,∠DBF+∠DFB=90°,
∵∠EFC=∠DFB,
∴∠DBF=∠ACD,
∵∠ABC=45°,
∴∠DCB=180°-90°-45°=45°,
∴∠DBC=∠DCB,
∴BD=CD,
在△BDF和△CDA中
∴△BDF≌△CDA(ASA)
∴BF=AC
【解析】【分析】利用垂直的定义可证得∠ADC=∠BDF=∠BEC=90°,利用三角形的内角和定理和余角的性质可证得∠DBF=∠ACD,再证明∠DBC=∠DCB,利用等角对等边,可证得BD=CD;再利用ASA证明△BDF≌△CDA,利用全等三角形的性质可证得结论.
16.【答案】证明:∵CA平分∠BCD,AE⊥BC,AF⊥CD,∴AE=AF.
在Rt△ABE和Rt△ADF中,∵
∴△ABE≌△ADF(HL).
【解析】【分析】由CA平分∠BCD,AE⊥BC于E,AF⊥CD,可得AE=AF,再由HL判定Rt△AEB≌Rt△AFD,即可得出结论.
17.【答案】解:∵∠1=∠2,OD⊥AD,OH⊥AE,∴OD=OH,在△DOG和△HOE中, ,∴△DOG≌△HOE,∴OG=OE
【解析】【分析】根据角平分线上的点到角两边的距离相等,得到OD=OH,再根据ASA,得到△DOG≌△HOE,得到OG=OE.
18.【答案】如图所示:
∴点C就是所求的点.
【解析】【分析】根据要求作出图象即可。
19.【答案】解:如图,作C关于OA的对称点C′,作D关于OB的对称点D′,连接C′D′交OA、OB于E、F;
∴AO垂直平分CC′,BO垂直平分DD′
∴CE=C′E,DF=D′F
∴小明走过的路线是:CE+EF+DF=C′E+EF+D′F=C′D′
根据两点之间线段最短可知:
小明所走的最短路线为C→E→F→D。
【解析】【分析】先作C关于OA的对称点C′,作D关于OB的对称点D′,连接C′D′交OA、OB于E、F,再根据垂直平分线的性质证出小明走过的路线是线段C′D′的长,根据两点之间线段最短可知此路线最短。
20.【答案】(1)解:设等腰三角形的地边长为x厘米,则腰长为2x厘米,由题意得:
x+2x+2x=20,解得:x=4,
∴该等腰三角形的各边的长为8cm、8cm、4cm;
(2)解:由题意可分:
①当5cm为该等腰三角形的腰长时,则底边长为20-2×5=10cm,
∵5+5=10,
∴不符合三角形三边关系;
②当5cm为该等腰三角形的底边长时,则腰长为(20-5)÷2=7.5cm,
∵5+7.5=12.5>7.5,
∴符合三角形的三边关系,
综上所述:能围成一条边是5cm的等腰三角形,其他两边长分别为7.5cm,7.5cm.
【解析】【分析】(1)设等腰三角形的地边长为x厘米,则腰长为2x厘米,根据题意列出方程x+2x+2x=20, 求解即可;
(2)分两种情况,再利用等腰三角形的性质及三角形三边的关系求解即可。
21.【答案】(1)解:∵△ABC和△ECD都是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°. ∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE. ∴△ACD≌△BCE. ∴AD=BE.
(2)解:BC垂直平分DE,理由如下: 如图,延长BC交DE于M, ∵∠ACB=60°,∠ACE=90°,∴∠ECM=180°-∠ACB-∠ACE=30°. ∵∠DCM=∠ECD-∠ECM=30°,∴∠ECM=∠DCM. ∵△ECD是等边三角形,∴CM垂直平分DE,即BC垂直平分DE.
【解析】【分析】(1)由等边三角形的性质易证∠BCE=∠ACD,然后用边角边可证 △ACD≌△BCE ,根据全等三角形的性质即可求得AD=BE;
(2) 延长BC交DE于M, 由等边三角形的性质和平角的性质可求得 ∠DCM=∠ECD-∠ECM=30°, 再根据等边三角形的三线合一即可求得CM是DE的垂直平分线。
22.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60°,
∵△BEF是等边三角形,
∴BE=BF,∠CBF+∠EBC=60°,
∴∠ABE=∠CBF,
在△ABE和△CBF, ,
∴△ABE≌△CBF(SAS);
(2)解:∵等边△ABC中,AD是∠BAC的角平分线,
∴∠BAE=30°,∠ACB=60°,
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30°,
∴∠ACF=∠BCF+∠ACB=30°+60°=90°
【解析】【分析】(1)根据等边三角形的性质得出AB=BC,∠ABE+∠EBC=60°,BE=BF,∠CBF+∠EBC=60°,从而得出∠ABE=∠CBF,利用SAS即可证出△ABE≌△CBF;
(2)根据等边三角形的性质得出∠BAE=30°,∠ACB=60°,再根据全等三角形的性质得出∠BCF=∠BAE=30°,利用∠ACF=∠BCF+∠ACB即可得出∠ACF的度数.
23.【答案】(1)证明: 如图,作PD⊥ON,
∵∠OAP+∠OBP=180° ,
∴∠PBD+∠OBP=180°,
∴∠OAP=∠PBD,
∵OP为∠MON的平分线,PD⊥ON,PC⊥OM,
∴PC=PD,
∴△PCA≌△PDB(AAS),
∴PA=PB;
(2)证明: ∵△PCA≌△PDB,
∴BD=AC,
∵PC=PD,OP=OP,
∴Rt△ODP≌Rt△OCP(HL),
∴OC=OD,
∴OA-OB=OC+AC-OB=OD-OB+AC=BD+AC=AC+AC=2AC.
【解析】【分析】(1)根据同角的补角相等得∠OAP=∠PBD,结合角平分线的性质,利用角角边定理证出△PCA≌△PDB,则对应边PA=PB;
(2)由△PCA≌△PDB,得出BD=AC,再利用斜边直角边定理证得Rt△ODP≌Rt△OCP,得出OC=OD,从而根据线段之间的关系推出OA-OB=2AC.
一、单选题
1.下列运动图标中,属于轴对称图形的是( )
A. B. C. D.
2.如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为( )
A.12 B.13 C.14 D.15
3.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
4.如图,将一张长方形纸片折叠,如果,则等于( )
A. B. C. D.
5.如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
A.PC=PD B.∠CPD=∠DOP C.∠CPO=∠DPO D.OC=OD
6.如图,平分,于点A,点Q是射线上的一个动点,若,则的最小值为( )
A.1 B.2 C.2.5 D.3
7.如图,D是AB边上的中点,将△ABC沿过D的直线折叠,使点A落在BC上F处,若∠B=50°,则∠BDF度数是( )
A.80° B.70° C.60° D.不确定
8.如图,将沿MN折叠,使,点A的对应点为点,若,,则的度数是( )
A. B. C. D.
9.如图,三角形纸片ABC中,∠A=65°,∠B=75°,将∠C沿DE对折,使点C落在△ABC外的点C′处,若∠1=20°,则∠2的度数为( )
A.80° B.90° C.100° D.110°
10.等腰中,,周长为,则的长为( )
A.15 B.12
C.15或12 D.以上都不正确
二、填空题
11.如图,将一个宽度相等的纸条按如图所示方法折叠,若,则 .
12.已知,在同一平面内,∠ABC=50°,AD∥BC,∠BAD的平分线交直线BC于点E,那么∠AEB的度数为 .
13.如图, ABC的周长为30cm,把 ABC的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC边于点E,连接AD,若AE=4cm,则 ABD的周长是 .
14.如图1是AD//BC的一张纸条,按图1—>图2—>图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=15°,则图2中∠AEF的度数为 .
三、解答题
15.已知:如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,CD与BE相交于点F.求证:BF=AC.
16.如图,在四边形ABCD中,AB=AD,CA平分∠BCD,AE⊥BC于点E,AF⊥CD交CD的延长线于点F.求证:△ABE≌△ADF.
17.已知,如图,OD⊥AD,OH⊥AE,DE交GH于O.若∠1=∠2,求证:OG=OE。
18.两个城镇、与两条公路,位置如图所示,其中是东西方向的公路.现电信部门需在处修建一座信号发射塔,要求发射塔到两个城镇、的距离必须相等,到两条公路,的距离也必须相等,且在的内部,请在图中,用尺规作图找出符合条件的点.(不写已知、求作、作法,只保留作图痕迹)
19.某班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子。BO桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到空座位D上.请你帮助他设计一条行走路线,使其所走的总路程最短
四、综合题
20.用一条长为20cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成一条边是5cm的等腰三角形吗?若能,求出其他两边;若不能,说明理由.
21.△ABC和△ECD都是等边三角形
(1)如图1,若B、C、D三点在一条直线上,求证:BE=AD;
(2)保持△ABC不动,将△ECD绕点C顺时针旋转,使∠ACE=90°(如图2),BC与DE有怎样的位置关系?说明理由.
22.如图,在等边三角形ABC中,AD是∠BAC的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接CF.
(1)求证:△ABE≌△CBF;
(2)求∠ACF的度数.
23.如图,已知:OP平分∠MON,点A,B 分别在边OM,ON 上,且∠OAP+∠OBP=180°, PC⊥OM于点C.
(1)求证:PA=PB;
(2)求证:OA-OB=2AC.
答案解析部分
1.【答案】B
【解析】【解答】解:A、不是轴对称图形,此选项不符合题意;
B、是轴对称图形,此选项符合题意;
C、不是轴对称图形,此选项不符合题意;
D、不是轴对称图形,此选项不符合题意.
故答案为:B.
【分析】把一个平面图形,沿着某一条直线折叠,直线两旁的部分能完全重合的平面图形就是轴对称图形,据此一一判断得出答案.
2.【答案】A
【解析】【解答】解:∵D为BC的中点,且BC=6,
∴BD= BC=3,
由折叠性质知NA=ND,
则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,
故答案为:A.
【分析】由折叠性质知NA=ND,根据中点定义BD= BC=3,根据三角形的周长计算方法及等量代换即可得出答案。
3.【答案】D
【解析】【解答】解:A、此标志不是轴对称图形,故A不符合题意;
B、此标志不是轴对称图形,故B不符合题意;
C、此标志不是轴对称图形,故C不符合题意;
D、此标志是轴对称图形,故D符合题意;
故答案为:D
【分析】轴对称图形是将一个图形沿某直线折叠后直线两旁的部分互相重合,再对各选项逐一判断.
4.【答案】C
【解析】【解答】解:如图:
∵AB∥CD,∠1=50°,∴∠CEH=∠1=50°,
∴∠HED=180°-∠CEH=180°-50°=130°,
由折叠得:∠HEF=∠FED=∠HED=65°,
∴∠α=∠FED=65°.
故选:C.
【分析】由平行线的性质可得∠CEH=∠1,由邻补角的定义可求得∠HED的度数,根据折叠的性质得∠HEF=∠FED=∠HED,然后根据平行线的性质可求解.
5.【答案】B
【解析】【解答】解:∵OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,
∴PC=PD,故A正确;
在Rt△OCP与Rt△ODP中,
,
∴△OCP≌△ODP,
∴∠CPO=∠DPO,OC=OD,故C、D正确.
不能得出∠CPD=∠DOP,故B错误.
故选B.
【分析】先根据角平分线的性质得出PC=PD,再利用HL证明△OCP≌△ODP,根据全等三角形的性质得出∠CPO=∠DPO,OC=OD.
6.【答案】D
【解析】【解答】解:由题意得当时将有最小值,
∵平分,于点A,,
∴,
故答案为:D
【分析】先根据题意得到当时将有最小值,进而根据角平分线的性质即可求解。
7.【答案】A
【解析】【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,∴AD=DF,∵D是AB边的中点,∴AD=BD,∴BD=DF,∴∠B=∠BFD,∵∠B=50°,∴∠BDF=180°-∠B-∠BFD=180°-50°-50°=80°,
故答案为:A.
【分析】根据点D是AB的中点结合翻折的性质可得到BD=DF,所以得到∠B=∠BFD,再利用三角形的内角和求解即可。
8.【答案】D
【解析】【解答】解:∵
∵,
,
由折叠的性质可知 ,
,
,
故答案为:D.
【分析】由平行线的性质可得∠MNC=180°-∠C=144°,由折叠可得 , ,结合三角形的内角和求出 ,从而求出 ,根据 即可求解.
9.【答案】C
【解析】【解答】解:∠A=65°,∠B=75°,∴∠C=∠C’=180°-∠A-∠B=40°,
由翻折变换的性质可得:∠DEC=∠DEC’,
∠DEC+∠DEB=∠DEC+∠DEC’-∠1=180°,
∴∠DEC=100°,
∴∠CDE=∠EDC’=180°-∠C-∠DEC=40°,
∴∠2=180°-∠CDE-∠EDC’=100°.
故答案为:C.
【分析】根据三角形的内角和定理及折叠的性质求出∠C=∠C’=180°-∠A-∠B=40°,∠DEC=∠DEC’,由图可知∠DEC+∠DEB=∠DEC+∠DEC’-∠1=180°,从中求出∠DEC=100°,进而可得∠CDE=∠EDC=40°,再根据平角的定义即可求出答案.
10.【答案】B
【解析】【解答】解:当时,,则;
当时,,但,故构不成三角形.
故答案为:B.
【分析】当AC=AB时,根据△ABC的周长为60可得BC的值;当BC=AB时,同理求出BC,然后结合三角形的三边关系进行判断.
11.【答案】74°
【解析】【解答】解:如图:
依题意得:AC∥DE,
∴∠2=∠CAD,
∵∠1=∠BAD=53°,
∴∠CAD=180°-(∠1+∠BAD)=74°,
∴∠2=74°.
故答案为:74°.
【分析】首先根据两直线平行,同位角相等可得∠2=∠CAD,再由翻折的性质可得∠1=∠BAD=53°,然后根据平角的定义可求出∠CAD=74°,据此可得出∠2的度数.
12.【答案】65°或25°
【解析】【解答】解:分情况讨论:(1)∵AE平分∠BAD,
∴∠EAD=∠EAB,
∵AD∥BC,
∴∠EAD=∠AEB,
∴∠BAD=∠AEB,
∵∠ABC=50°,
∴∠AEB= (180°-50°)=65°.(2)∵AE平分∠BAD,
∴∠EAD=∠EAB= ,
∵AD∥BC,
∴∠AEB=∠DAE= ,∠DAB=∠ABC,
∵∠ABC=50°,
∴∠AEB= ×50°=25°.
故答案为:65°或25°.
【分析】首先根据角平分线的定义得出∠EAD=∠EAB,再分情况讨论计算即可.
13.【答案】22cm
【解析】【解答】解:根据折叠方法可得AE=CE,AD=CD,
∵AE=4cm,
∴CE=4cm,
∵△ABC的周长为30cm,
∴AB+CB=30-8=22(cm),
△ABD的周长是:AB+BD+AD=AB+BC=22cm
【分析】由折叠的性质可得AE=CE=4cm,AD=CD,利用△ABC的周长求出AB+BC的长,从而求出△ABD的周长.
14.【答案】115°
【解析】【解答】解:如图,设∠B'FE=x,
当纸条沿EF折叠时,
∴∠BFE=∠B'FE=x,∠AEF=∠A'EF,
∴∠BFC=∠BFE-∠CFE=x-15°,
当纸条沿BF折叠时,
∴∠C'FB=∠CFB=x-15°,
∵∠B'FE+∠BFE+∠CFB=180°,
∴x+x+x-15°=180°,
解得x=65°,
∵A'D'∥B'C',
∴∠A'EF=180°-∠B'FE=180°-65°=115°,
∴∠AEF=115°.
故答案为:115°.
【分析】设∠B'FE=x,根据折叠的性质得∠BFE=∠B'FE=x,∠AEF=∠A'EF, 则∠BFC=x-15°, 再由两次折叠后得到∠CFB=∠BFC=x-15°,然后根据平角定义列方程求解,再根据平行线的性质得∠A'EF=180°-∠B'FE=115°,最后根据折叠的性质得出∠AEF=115°.
15.【答案】证明:CD⊥AB,BE⊥AC,
∴∠ADC=∠BDF=∠BEC=90°,
∴∠ACD+∠EFC=90°,∠DBF+∠DFB=90°,
∵∠EFC=∠DFB,
∴∠DBF=∠ACD,
∵∠ABC=45°,
∴∠DCB=180°-90°-45°=45°,
∴∠DBC=∠DCB,
∴BD=CD,
在△BDF和△CDA中
∴△BDF≌△CDA(ASA)
∴BF=AC
【解析】【分析】利用垂直的定义可证得∠ADC=∠BDF=∠BEC=90°,利用三角形的内角和定理和余角的性质可证得∠DBF=∠ACD,再证明∠DBC=∠DCB,利用等角对等边,可证得BD=CD;再利用ASA证明△BDF≌△CDA,利用全等三角形的性质可证得结论.
16.【答案】证明:∵CA平分∠BCD,AE⊥BC,AF⊥CD,∴AE=AF.
在Rt△ABE和Rt△ADF中,∵
∴△ABE≌△ADF(HL).
【解析】【分析】由CA平分∠BCD,AE⊥BC于E,AF⊥CD,可得AE=AF,再由HL判定Rt△AEB≌Rt△AFD,即可得出结论.
17.【答案】解:∵∠1=∠2,OD⊥AD,OH⊥AE,∴OD=OH,在△DOG和△HOE中, ,∴△DOG≌△HOE,∴OG=OE
【解析】【分析】根据角平分线上的点到角两边的距离相等,得到OD=OH,再根据ASA,得到△DOG≌△HOE,得到OG=OE.
18.【答案】如图所示:
∴点C就是所求的点.
【解析】【分析】根据要求作出图象即可。
19.【答案】解:如图,作C关于OA的对称点C′,作D关于OB的对称点D′,连接C′D′交OA、OB于E、F;
∴AO垂直平分CC′,BO垂直平分DD′
∴CE=C′E,DF=D′F
∴小明走过的路线是:CE+EF+DF=C′E+EF+D′F=C′D′
根据两点之间线段最短可知:
小明所走的最短路线为C→E→F→D。
【解析】【分析】先作C关于OA的对称点C′,作D关于OB的对称点D′,连接C′D′交OA、OB于E、F,再根据垂直平分线的性质证出小明走过的路线是线段C′D′的长,根据两点之间线段最短可知此路线最短。
20.【答案】(1)解:设等腰三角形的地边长为x厘米,则腰长为2x厘米,由题意得:
x+2x+2x=20,解得:x=4,
∴该等腰三角形的各边的长为8cm、8cm、4cm;
(2)解:由题意可分:
①当5cm为该等腰三角形的腰长时,则底边长为20-2×5=10cm,
∵5+5=10,
∴不符合三角形三边关系;
②当5cm为该等腰三角形的底边长时,则腰长为(20-5)÷2=7.5cm,
∵5+7.5=12.5>7.5,
∴符合三角形的三边关系,
综上所述:能围成一条边是5cm的等腰三角形,其他两边长分别为7.5cm,7.5cm.
【解析】【分析】(1)设等腰三角形的地边长为x厘米,则腰长为2x厘米,根据题意列出方程x+2x+2x=20, 求解即可;
(2)分两种情况,再利用等腰三角形的性质及三角形三边的关系求解即可。
21.【答案】(1)解:∵△ABC和△ECD都是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD=60°. ∴∠ACB+∠ACE=∠ECD+∠ACE,即∠ACD=∠BCE. ∴△ACD≌△BCE. ∴AD=BE.
(2)解:BC垂直平分DE,理由如下: 如图,延长BC交DE于M, ∵∠ACB=60°,∠ACE=90°,∴∠ECM=180°-∠ACB-∠ACE=30°. ∵∠DCM=∠ECD-∠ECM=30°,∴∠ECM=∠DCM. ∵△ECD是等边三角形,∴CM垂直平分DE,即BC垂直平分DE.
【解析】【分析】(1)由等边三角形的性质易证∠BCE=∠ACD,然后用边角边可证 △ACD≌△BCE ,根据全等三角形的性质即可求得AD=BE;
(2) 延长BC交DE于M, 由等边三角形的性质和平角的性质可求得 ∠DCM=∠ECD-∠ECM=30°, 再根据等边三角形的三线合一即可求得CM是DE的垂直平分线。
22.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=BC,∠ABE+∠EBC=60°,
∵△BEF是等边三角形,
∴BE=BF,∠CBF+∠EBC=60°,
∴∠ABE=∠CBF,
在△ABE和△CBF, ,
∴△ABE≌△CBF(SAS);
(2)解:∵等边△ABC中,AD是∠BAC的角平分线,
∴∠BAE=30°,∠ACB=60°,
∵△ABE≌△CBF,
∴∠BCF=∠BAE=30°,
∴∠ACF=∠BCF+∠ACB=30°+60°=90°
【解析】【分析】(1)根据等边三角形的性质得出AB=BC,∠ABE+∠EBC=60°,BE=BF,∠CBF+∠EBC=60°,从而得出∠ABE=∠CBF,利用SAS即可证出△ABE≌△CBF;
(2)根据等边三角形的性质得出∠BAE=30°,∠ACB=60°,再根据全等三角形的性质得出∠BCF=∠BAE=30°,利用∠ACF=∠BCF+∠ACB即可得出∠ACF的度数.
23.【答案】(1)证明: 如图,作PD⊥ON,
∵∠OAP+∠OBP=180° ,
∴∠PBD+∠OBP=180°,
∴∠OAP=∠PBD,
∵OP为∠MON的平分线,PD⊥ON,PC⊥OM,
∴PC=PD,
∴△PCA≌△PDB(AAS),
∴PA=PB;
(2)证明: ∵△PCA≌△PDB,
∴BD=AC,
∵PC=PD,OP=OP,
∴Rt△ODP≌Rt△OCP(HL),
∴OC=OD,
∴OA-OB=OC+AC-OB=OD-OB+AC=BD+AC=AC+AC=2AC.
【解析】【分析】(1)根据同角的补角相等得∠OAP=∠PBD,结合角平分线的性质,利用角角边定理证出△PCA≌△PDB,则对应边PA=PB;
(2)由△PCA≌△PDB,得出BD=AC,再利用斜边直角边定理证得Rt△ODP≌Rt△OCP,得出OC=OD,从而根据线段之间的关系推出OA-OB=2AC.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
