2024年上海市建平实验学校九年级下学期月考数学试卷(含解析)
文档属性
| 名称 | 2024年上海市建平实验学校九年级下学期月考数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 11:17:47 | ||
图片预览



文档简介
上海市建平实验中学2023学年第二学期阶段练习(2)
初三数学
一、选择题:本题共6小题,每小题4分,共24分.每题只有一项是符合题目要求的.
1. 下列实数中,无理数的是( )
A. 5 B. C. D.
2. 下列计算正确是( )
A. B. C. D.
3. 下列用于证明勾股定理的图形中,是轴对称图形的是( )
A. B. C. D.
4. 若反比例函数,y随x增大而增大,则的图像大致是( )
A. B. C. D.
5. 下列四个命题:①平行四边形的两组对角分别相等;②对角线互相垂直且平分的四边形是菱形;③矩形是轴对称图形;④对角线相等的菱形是正方形;其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
6. 如图,是的直径,若,连接,,则的度数是( )
A. B. C. D.
二、填空题:本题共12小题,每小题4分,共48分.
7. 的相反数是_________________;
8. 在函数中,自变量x的取值范围为_______.
9. 方程 =0解是_______.
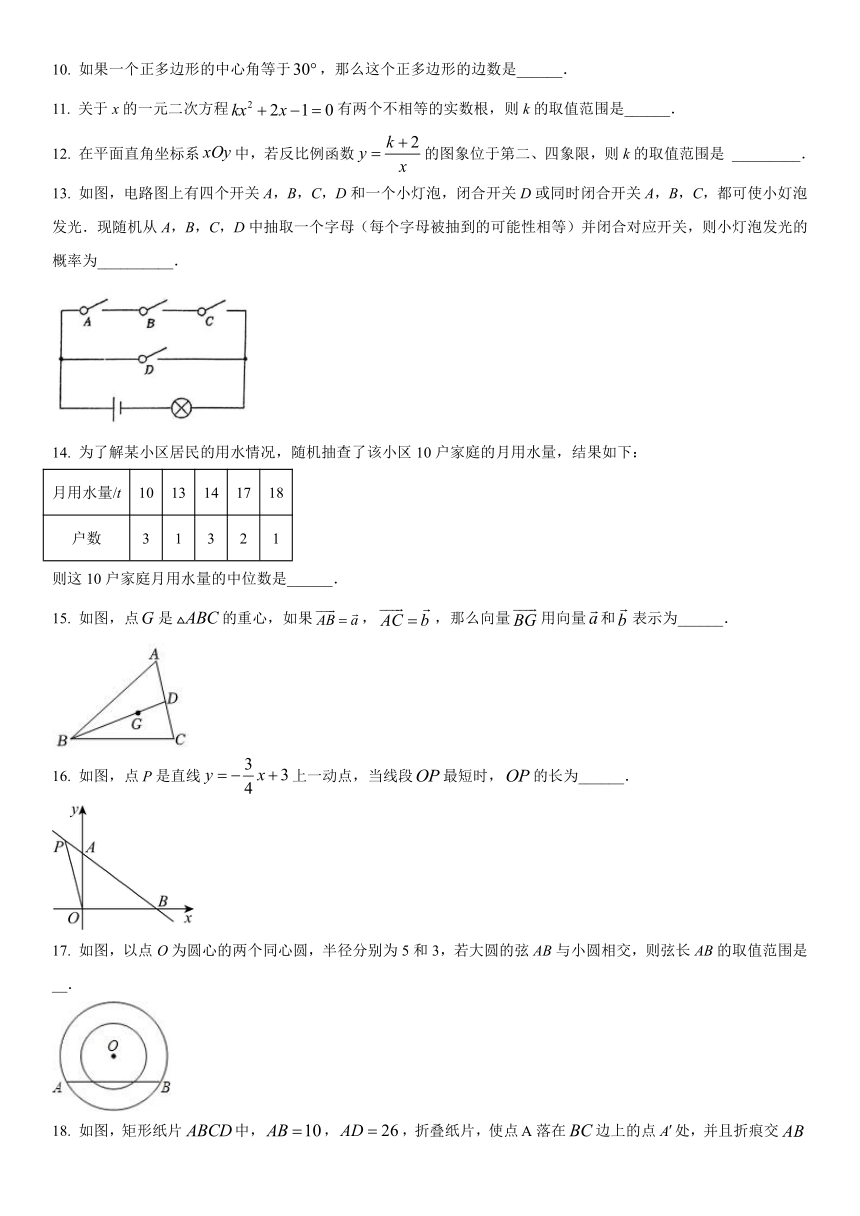
10. 如果一个正多边形的中心角等于,那么这个正多边形的边数是______.
11. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
12. 在平面直角坐标系中,若反比例函数的图象位于第二、四象限,则k的取值范围是 _________.
13. 如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小奵泡发光.现随机从A,B,C,D中抽取一个字母(每个字母被抽到的可能性相等)并闭合对应开关,则小灯泡发光的概率为__________.
14. 为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量/t 10 13 14 17 18
户数 3 1 3 2 1
则这10户家庭月用水量的中位数是______.
15. 如图,点是的重心,如果,,那么向量用向量和表示为______.
16. 如图,点是直线上一动点,当线段最短时,的长为______.
17. 如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是 __.
18. 如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为______.
三、解答题:本题共7小题,共78分.解答应写出文字说明,证明过程或演算步骤.
19. 计算;(-)-1+tan30°+|1-|-
20. 解不等式组:
21. 如图,在中,,以点O为圆心,长为半径的圆交于点C,点D在边上,且.
(1)判断直线与位置关系,并说明理由;
(2)若,求的半径.
22. 阅读理解:七年级一班数学学习兴趣小组在解决下列问题中,发现该类问题可以“建立直角坐标系、应用一次函数”解决问题.请先阅读下列解决问题的方法,然后再应用此方法解决后续问题.
问题:如图①,直立在点处标杆长,站立在点处的观察者从点处看到标杆顶、旗杆顶在一条直线上.已知,,,求旗杆高.
解:建立如图②所示直角坐标系,则线段可看作一个一次函数的图象
由题意可得各点坐标为:点,,,且所求高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得
∴
当时,,即.
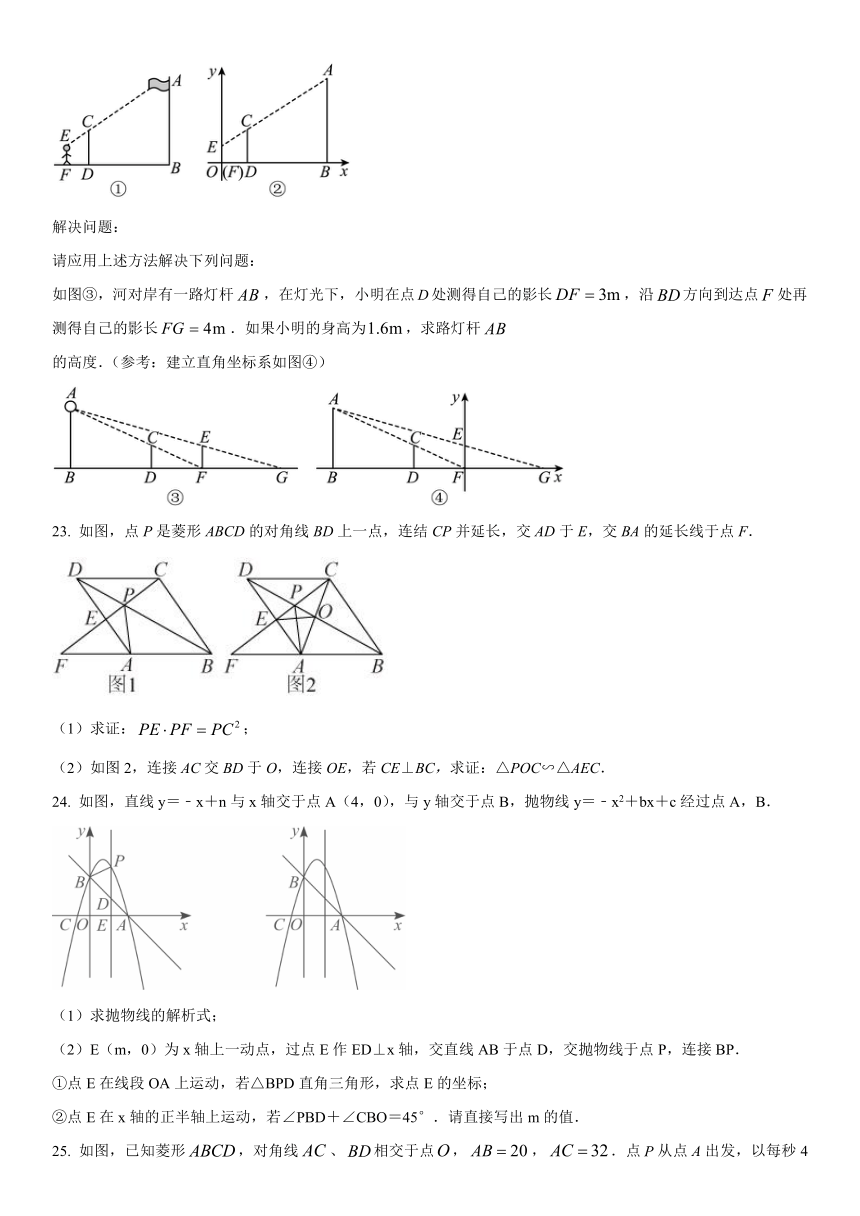
解决问题:
请应用上述方法解决下列问题:
如图③,河对岸有一路灯杆,在灯光下,小明在点处测得自己的影长,沿方向到达点处再测得自己的影长.如果小明的身高为,求路灯杆
的高度.(参考:建立直角坐标系如图④)
23. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:;
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
24. 如图,直线y=﹣x+n与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求抛物线的解析式;
(2)E(m,0)为x轴上一动点,过点E作ED⊥x轴,交直线AB于点D,交抛物线于点P,连接BP.
①点E在线段OA上运动,若△BPD直角三角形,求点E的坐标;
②点E在x轴的正半轴上运动,若∠PBD+∠CBO=45°.请直接写出m的值.
25. 如图,已知菱形,对角线、相交于点,,.点从点A出发,以每秒4个单位的速度沿线段向点运动,同付,点从点出发,以每秒3个单位的速度沿折线向点运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接、、,设点的运动时间为秒.
(1)求线段的长;
(2)在整个运动过程中,能否成为直角三角形?若能,请求出符合题意的t的值;若不能,请说明理由;
(3)以为圆心,为半径作,当与线段只有一个公共点时,求的值或的取值范围.
上海市建平实验中学2023学年第二学期阶段练习(2)
初三数学
一、选择题:本题共6小题,每小题4分,共24分.每题只有一项是符合题目要求的.
1. 下列实数中,无理数的是( )
A. 5 B. C. D.
【答案】C
【分析】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,等;开方开不尽得到的数;以及像0.1010010001…(两个1之间依次多一个0),等有这样规律的数.
根据无限不循环小数是无理数判定即可.
【详解】解:A、5是整数,不是无理数,故此选项不符合题意;
B、是分数,不是无理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、整数,不是无理数,故此选项不符合题意;
故选:C.
2. 下列计算正确的是( )
A B. C. D.
【答案】C
【分析】本题考查合并同类项、同底数幂的除法、积的乘方、完全平方公式,根据相关运算法则逐项计算即可.
【详解】解:A,,计算错误;
B,,计算错误;
C,,计算正确;
D,,计算错误;
故选C.
3. 下列用于证明勾股定理的图形中,是轴对称图形的是( )
A. B. C. D.
【答案】C
【分析】本题考查轴对称图形,关键是掌握轴对称图形的定义.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
【详解】解:A、B、D中的图形不是轴对称图形,故A、B、D不符合题意;
C中的图形是轴对称图形,故C符合题意;
故选:C.
4. 若反比例函数,y随x增大而增大,则的图像大致是( )
A. B. C. D.
【答案】D
【分析】根据反比例函数,y随x增大而增大,得出,则中,y随x的增大而减小,结合得出与y轴交于负半轴,即可得出结论.
【详解】解:∵反比例函数,y随x增大而增大,
∴,
∴中,y随x的增大而减小,
∵,
∴与y轴交于负半轴,
故选:D.
【点睛】本题主要考查了一次函数和反比例函数的性质,解题的关键是熟练掌握一次函数和反比例函数的增减性.
5. 下列四个命题:①平行四边形的两组对角分别相等;②对角线互相垂直且平分的四边形是菱形;③矩形是轴对称图形;④对角线相等的菱形是正方形;其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【分析】根据平行四边形、矩形的性质定理以及菱形、正方形的判定定理进行判断即可.
【详解】解:由题意知,平行四边形的两组对角分别相等是真命题,故①符合要求;
对角线互相垂直且平分的四边形是菱形是真命题;故②符合要求;
矩形是轴对称图形是真命题;故③符合要求;
对角线相等的菱形是正方形是真命题;故④符合要求;
∴真命题有4个,
故选:D.
【点睛】本题考查了平行四边形、矩形的性质定理以及菱形、正方形的判定定理,真命题等知识.解题的关键在于对知识的熟练掌握.
6. 如图,是的直径,若,连接,,则的度数是( )
A. B. C. D.
【答案】C
【分析】本题考查了圆心角的性质,圆的内接四边形互补,等边三角形的判定,解题的关键是求出.
【详解】解:如下图,连结,
,
,
,
,
故选:C.
二、填空题:本题共12小题,每小题4分,共48分.
7. 的相反数是_________________;
【答案】2
【分析】根据只有符号不同的两个数叫做互为相反数解答即可.
【详解】2的相反数是2.
故答案为2.
【点睛】本题考查了实数的性质,熟记概念与性质是解题的关键.
8. 在函数中,自变量x的取值范围为_______.
【答案】
【分析】本题考查了函数的取值范围,解题的关键是知晓分式有意义的条件.
根据函数中分式的分母不为0即可得到答案.
【详解】当分式的分母为零时,分式才没有意义,故.
即自变量x的取值范围为.
故答案为:.
9. 方程 =0的解是_______.
【答案】1
【分析】首先根据二次根式有意义的条件,判定x的取值范围,然后方程两边同时平方,解一元二次方程即可得解.
【详解】根据题意,得
解得
将方程两边平方,得
解得
综上,
【点睛】此题主要考查二次根式有意义的条件以及一元二次方程的求解,熟练掌握,即可解题.
10. 如果一个正多边形的中心角等于,那么这个正多边形的边数是______.
【答案】12
【分析】本题考查正多边形的中心角与边数之间的关系,根据正边形的中心角为,即可解题.
【详解】解:设这个正多边形的边数是,且一个正多边形的中心角等于,
有,解得,
故答案为:12.
11. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
【答案】且
【分析】本题考查了根的判别式,根据方程的根的判别式且计算即可.
【详解】∵一元二次方程有两个不相等的实数根,
∴且,
解得且,
故答案为:且.
12. 在平面直角坐标系中,若反比例函数的图象位于第二、四象限,则k的取值范围是 _________.
【答案】
【分析】本题考查反比例函数的性质,解题的关键是掌握当时,的图象位于第二、四象限.根据反比例函数的性质列不等式即可解得答案.
【详解】解:反比例函数的图象位于第二、四象限,
,
解得,
故答案为:
13. 如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小奵泡发光.现随机从A,B,C,D中抽取一个字母(每个字母被抽到的可能性相等)并闭合对应开关,则小灯泡发光的概率为__________.
【答案】
【分析】本题考查用概率公式计算事件发生的概率,熟练掌握概率公式:是解题的关键.
所有可能的结果共有4种可能,而让小灯泡发光的只有抽到D,一种可能,由概率公式即可求解.
【详解】解:小灯泡发光的概率为.
故答案为:.
14. 为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量/t 10 13 14 17 18
户数 3 1 3 2 1
则这10户家庭月用水量的中位数是______.
【答案】14吨
【分析】本题考查了求中位数,正确理解中位数的定义是解题的关键.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.根据中位数的定义,即得答案.
【详解】将表中数据为从小到大排列,处在第5位、第6位的是14吨,
所以这10户家庭月用水量的中位数是14吨.
故答案为:14吨..
15. 如图,点是的重心,如果,,那么向量用向量和表示为______.
【答案】##
【分析】由是的重心,推出,,求出,可得结论.
【详解】解:∵G是的重心,
∴,,
∵,
∴,
故答案为:.
【点睛】本题考查三角形的重心,三角形法则等知识,解题的关键是掌握重心的性质,学会利用三角形法则解决问题.
16. 如图,点是直线上一动点,当线段最短时,的长为______.
【答案】
【分析】根据直线解析式求出点A、B的坐标,再根据勾股定理求出AB的长度,根据点到直线的所有线段中,垂线段最短,利用三角形的面积列式即可求解.
【详解】解:当时,,
当时,,
解得,
∴点A、B的坐标是,,
∴,
根据垂线段最短性质,时,最短,如点所示
此时,,
即,
解得,即.
故答案为:.
【点睛】本题综合考查了一次函数的问题,主要利用勾股定理,垂线段最短的性质,根据直线解析式求出点A、B的坐标是解题的关键.
17. 如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是 __.
【答案】
【分析】此题可以首先计算出当AB与小圆相切的时候的弦长.连接过切点的半径和大圆的一条半径,根据勾股定理和垂径定理,得AB=8.若大圆的弦AB与小圆有两个公共点,即相交,此时AB>8;又因为大圆最长的弦是直径10,则8<AB≤10.
【详解】解:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴.
当AB过圆心时最长即为大圆的直径10,
∴8<AB≤10.
故答案为:8<AB≤10.
【点睛】本题综合运用了切线的性质、勾股定理和垂径定理.此题可以首先计算出和小圆相切时的弦长,再进一步分析相交时的弦长.
18. 如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为______.
【答案】
【分析】设,则,当与重合时,证得即,进而利用勾股定理得,当与重合时,,即可得解.
【详解】解:设,则,
当与重合时,如下图,
∵四边形是矩形,
∴,,,
由折叠的性质可得,,
,
∴,
∴,
∴,
∴即,
解得,
∵,
∴即,
解得或(舍去),
当与重合时,如下图,
此时,
∴,
故答案为:.
【点睛】本题主要考查了勾股定理,相似三角形的判定及性质,折叠的性质,矩形的性质,熟练掌握矩形的性质及相似三角形的判定及性质是解题的关键.
三、解答题:本题共7小题,共78分.解答应写出文字说明,证明过程或演算步骤.
19. 计算;(-)-1+tan30°+|1-|-
【答案】-2-
【分析】直接利用绝对值的性质以及二次根式的性质、特殊角的三角函数值分别化简得出答案.
【详解】解:原式=-2+×+-1-2
=-2-.
【点睛】此题主要考查了实数运算,正确化简各数是解题关键.
20. 解不等式组:
【答案】
【分析】本题主要考查了解一元一次不等式组,先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:
解不等式①,得,
解不等式②,得,
∴不等式组的解集为.
21. 如图,在中,,以点O为圆心,长为半径的圆交于点C,点D在边上,且.
(1)判断直线与的位置关系,并说明理由;
(2)若,求半径.
【答案】(1)直线与相切,理由见解析
(2)
【分析】本题考查了切线的证明、正切的应用等知识点,掌握相关几何结论是解题关键.
(1)连接,由得,结合,即可求解;
(2)设的半径为,可得,根据可得,即可求解;
【小问1详解】
解:直线与相切,理由如下:
连接,如图所示:
则
∴
∵
∴
∵
∴
∴
∵为半径,
∴直线与相切
【小问2详解】
解:设的半径为,
∵
∴,
∴
∵
∴,
解得:
22. 阅读理解:七年级一班数学学习兴趣小组在解决下列问题中,发现该类问题可以“建立直角坐标系、应用一次函数”解决问题.请先阅读下列解决问题的方法,然后再应用此方法解决后续问题.
问题:如图①,直立在点处的标杆长,站立在点处的观察者从点处看到标杆顶、旗杆顶在一条直线上.已知,,,求旗杆高.
解:建立如图②所示直角坐标系,则线段可看作一个一次函数的图象
由题意可得各点坐标为:点,,,且所求的高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得
∴
当时,,即.
解决问题:
请应用上述方法解决下列问题:
如图③,河对岸有一路灯杆,在灯光下,小明在点处测得自己的影长,沿方向到达点处再测得自己的影长.如果小明的身高为,求路灯杆
的高度.(参考:建立直角坐标系如图④)
【答案】
【分析】根据题中的例题过程连求两次一次函数解析式作答即可.
【详解】由题意可得各点坐标为:,,且所求的高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得.
∴直线的函数关系式为①.
∵直线过点,,
同理可得直线的解析式为②,
联立①②解得,,
答:路灯杆的高度.
【点睛】本题考查了求两直线的交点和对例题的理解应用能力,题目不难,但注意做题时需要运用题目所给方式做题而不能用其他的解答方法.
23. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:;
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)根据菱形的性质,首先利用SAS证明△CDP≌△ADP,得PC=PA,∠DCP=∠DAP,再说明△PAE∽△PFA,得,即可证明结论;
(2)根据菱形的性质可说明∠COP=∠CEA,从而证明结论.
【小问1详解】
证明:∵四边形ABCD菱形,
∴AD=CD,∠CDP=∠ADP,,
在△CDP和△ADP中,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP,
∵,
∴∠DCP=∠F,
∴∠DAP=∠F,
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴,
∴PA2=PE PF,
∴PE PF=PC2;
【小问2详解】
∵CE⊥BC,
∴∠ECB=90°,
∵,
∴∠CEA=∠BCE=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COP=90°,
∴∠COP=∠CEA,
∵∠OCP=∠ECA,
∴△POC∽△AEC.
【点睛】本题主要考查了菱形的性质,相似三角形的判定与性质,全等三角形的判定与性质,证明PA=PC是解决问题(1)的关键.
24. 如图,直线y=﹣x+n与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求抛物线解析式;
(2)E(m,0)为x轴上一动点,过点E作ED⊥x轴,交直线AB于点D,交抛物线于点P,连接BP.
①点E在线段OA上运动,若△BPD直角三角形,求点E的坐标;
②点E在x轴的正半轴上运动,若∠PBD+∠CBO=45°.请直接写出m的值.
【答案】(1)y=﹣x2+3x+4;(2)① E(2,0)或(3,0);②m=7或.
【分析】(1)将点A坐标代入直线解析式可求n的值,可求点B坐标,利用待定系数法可求解;
(2)①分两种情况讨论,勾股定理可求解;②分两种情况讨论,由相似三角形的性质和等腰三角形的性质,可求BP解析式,联立方程可求解.
【详解】解:(1)∵直线y=﹣x+n与x轴交于点A(4,0),
∴0=﹣4+n,
∴n=4,
∴直线解析式为:y=﹣x+4,
当x=0时,y=4,
∴点B(0,4),
∵抛物线y=﹣x2+bx+c经过点A,B,则,解得,
∴抛物线的解析式为:y=﹣x2+3x+4①;
(2)①∵ED⊥x轴,
∴∠PEA=90°,
∴∠BDP=∠ADE<90°,
设点E(m,0),点P(m,﹣m2+3m+4),则点D(m,﹣m+4),
∴PD2=(﹣m2+4m)2,BP2=m2+(﹣m2+3m)2,BD2=m2+(﹣m+4﹣4)2=2m2,
当∠PBD=90°时,BP2+BD2=PD2,
∴m2+(﹣m2+3m)2+2m2=(﹣m2+4m)2,
∴m=2,m=0(舍去)
∴点E的坐标为(2,0),
当∠BPD=90°时,BP2+PD2=BD2,
同理可得:m=0(舍去)或3或4(舍去),
∴点E的坐标为(3,0),
综上所述:点E的坐标为(2,0)或(3,0);
②当点P在x轴上方时,如图1,连接BC,延长BP交x轴于N,
∵点A(4,0),点B(0,4),
∴OA=OB=4,
∴∠BAO=∠ABO=45°,
∵抛物线y=﹣x2+3x+4与x轴交于点A,点C,
∴0=﹣x2+3x+4,
∴x1=4,x2=﹣1,
∴点C(﹣1,0),
∴OC=1,
∵∠PBD+∠CBO=45°,∠BAO=∠PBD+∠BNO=45°,
∴∠CBO=∠BNO,
又∵∠BOC=∠BON=90°,
∴△BCO∽△NBO,
∴,
∴,
∴ON=16,
∴点N(16,0),
∴直线BN解析式为:yx+4②,
联立①②并解得:x=0(舍去)或,
∴m;
当点P在x轴下方时,如图2,连接BC,设BP与x轴交于点H,
∵∠PBD+∠CBO=45°,∠OBH+∠PBD=45°,
∴∠CBO=∠OBH,
又∵OB=OB,∠COB=∠BOH,
∴△BOH≌△BOC(ASA),
∴OC=OH=1,
∴点H(1,0),
∴直线BH解析式为:y=﹣4x+4③,
联立①③并解得:x=0(舍去)或7,
∴点P的横坐标为7,
∴m=7,
综上所述:m=7或.
【点睛】本题是二次函数综合题,考查了二次函数的性质,待定系数法求解析式,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.
25. 如图,已知菱形,对角线、相交于点,,.点从点A出发,以每秒4个单位的速度沿线段向点运动,同付,点从点出发,以每秒3个单位的速度沿折线向点运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接、、,设点的运动时间为秒.
(1)求线段的长;
(2)在整个运动过程中,能否成为直角三角形?若能,请求出符合题意的t的值;若不能,请说明理由;
(3)以为圆心,为半径作,当与线段只有一个公共点时,求的值或的取值范围.
【答案】(1)12 (2)能,或
(3)或
【分析】(1)首先根据四边形是菱形,可得,,,利用勾股定理即可求出.
(2)情形1:如图1中,当时,,利用得列出方程求解;情形2:如图2,当时,,作垂足为,利用得到列出方程即可解决.
(3)情形1:如图3,当点在线段上时,与线段相切于,连接,此时与线段只有一个交点,利用得到列出方程解决.
情形2:如图4,当时,作垂足为,由得到列出方程求解.
【小问1详解】
解: 四边形是菱形,
,,,
,
,
在中,,,
.
【小问2详解】
解:能.理由如下:
如图1,当时,,
,,
,
,
,
,
,
或不合题意舍弃)
.
如图2,当时,,作垂足为,
,
,
,
,,,,
,,
,
,
,
,
,
解得或不合题意舍弃)
综上所述或时是直角三角形.
【小问3详解】
解:①如图3,当点在线段上时,与线段相切于,连接,
此时与线段只有一个交点,
在中,,,
,
,,
,
,
,解得或不合题意舍弃).
②如图4,当时,作垂足为,
,,
,
,
,解得.
时与线段只有一个交点.
综上所述或时与线段只有一个交点.
【点睛】本题考查菱形的性质、勾股定理、相似三角形的判定和性质、圆的有关知识,学会分类讨论是解题的关键,解题中培养动手画图能力,利用转化的数学思想去思考问题.
初三数学
一、选择题:本题共6小题,每小题4分,共24分.每题只有一项是符合题目要求的.
1. 下列实数中,无理数的是( )
A. 5 B. C. D.
2. 下列计算正确是( )
A. B. C. D.
3. 下列用于证明勾股定理的图形中,是轴对称图形的是( )
A. B. C. D.
4. 若反比例函数,y随x增大而增大,则的图像大致是( )
A. B. C. D.
5. 下列四个命题:①平行四边形的两组对角分别相等;②对角线互相垂直且平分的四边形是菱形;③矩形是轴对称图形;④对角线相等的菱形是正方形;其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
6. 如图,是的直径,若,连接,,则的度数是( )
A. B. C. D.
二、填空题:本题共12小题,每小题4分,共48分.
7. 的相反数是_________________;
8. 在函数中,自变量x的取值范围为_______.
9. 方程 =0解是_______.
10. 如果一个正多边形的中心角等于,那么这个正多边形的边数是______.
11. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
12. 在平面直角坐标系中,若反比例函数的图象位于第二、四象限,则k的取值范围是 _________.
13. 如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小奵泡发光.现随机从A,B,C,D中抽取一个字母(每个字母被抽到的可能性相等)并闭合对应开关,则小灯泡发光的概率为__________.
14. 为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量/t 10 13 14 17 18
户数 3 1 3 2 1
则这10户家庭月用水量的中位数是______.
15. 如图,点是的重心,如果,,那么向量用向量和表示为______.
16. 如图,点是直线上一动点,当线段最短时,的长为______.
17. 如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是 __.
18. 如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为______.
三、解答题:本题共7小题,共78分.解答应写出文字说明,证明过程或演算步骤.
19. 计算;(-)-1+tan30°+|1-|-
20. 解不等式组:
21. 如图,在中,,以点O为圆心,长为半径的圆交于点C,点D在边上,且.
(1)判断直线与位置关系,并说明理由;
(2)若,求的半径.
22. 阅读理解:七年级一班数学学习兴趣小组在解决下列问题中,发现该类问题可以“建立直角坐标系、应用一次函数”解决问题.请先阅读下列解决问题的方法,然后再应用此方法解决后续问题.
问题:如图①,直立在点处标杆长,站立在点处的观察者从点处看到标杆顶、旗杆顶在一条直线上.已知,,,求旗杆高.
解:建立如图②所示直角坐标系,则线段可看作一个一次函数的图象
由题意可得各点坐标为:点,,,且所求高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得
∴
当时,,即.
解决问题:
请应用上述方法解决下列问题:
如图③,河对岸有一路灯杆,在灯光下,小明在点处测得自己的影长,沿方向到达点处再测得自己的影长.如果小明的身高为,求路灯杆
的高度.(参考:建立直角坐标系如图④)
23. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:;
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
24. 如图,直线y=﹣x+n与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求抛物线的解析式;
(2)E(m,0)为x轴上一动点,过点E作ED⊥x轴,交直线AB于点D,交抛物线于点P,连接BP.
①点E在线段OA上运动,若△BPD直角三角形,求点E的坐标;
②点E在x轴的正半轴上运动,若∠PBD+∠CBO=45°.请直接写出m的值.
25. 如图,已知菱形,对角线、相交于点,,.点从点A出发,以每秒4个单位的速度沿线段向点运动,同付,点从点出发,以每秒3个单位的速度沿折线向点运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接、、,设点的运动时间为秒.
(1)求线段的长;
(2)在整个运动过程中,能否成为直角三角形?若能,请求出符合题意的t的值;若不能,请说明理由;
(3)以为圆心,为半径作,当与线段只有一个公共点时,求的值或的取值范围.
上海市建平实验中学2023学年第二学期阶段练习(2)
初三数学
一、选择题:本题共6小题,每小题4分,共24分.每题只有一项是符合题目要求的.
1. 下列实数中,无理数的是( )
A. 5 B. C. D.
【答案】C
【分析】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,等;开方开不尽得到的数;以及像0.1010010001…(两个1之间依次多一个0),等有这样规律的数.
根据无限不循环小数是无理数判定即可.
【详解】解:A、5是整数,不是无理数,故此选项不符合题意;
B、是分数,不是无理数,故此选项不符合题意;
C、是无理数,故此选项符合题意;
D、整数,不是无理数,故此选项不符合题意;
故选:C.
2. 下列计算正确的是( )
A B. C. D.
【答案】C
【分析】本题考查合并同类项、同底数幂的除法、积的乘方、完全平方公式,根据相关运算法则逐项计算即可.
【详解】解:A,,计算错误;
B,,计算错误;
C,,计算正确;
D,,计算错误;
故选C.
3. 下列用于证明勾股定理的图形中,是轴对称图形的是( )
A. B. C. D.
【答案】C
【分析】本题考查轴对称图形,关键是掌握轴对称图形的定义.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,由此即可判断.
【详解】解:A、B、D中的图形不是轴对称图形,故A、B、D不符合题意;
C中的图形是轴对称图形,故C符合题意;
故选:C.
4. 若反比例函数,y随x增大而增大,则的图像大致是( )
A. B. C. D.
【答案】D
【分析】根据反比例函数,y随x增大而增大,得出,则中,y随x的增大而减小,结合得出与y轴交于负半轴,即可得出结论.
【详解】解:∵反比例函数,y随x增大而增大,
∴,
∴中,y随x的增大而减小,
∵,
∴与y轴交于负半轴,
故选:D.
【点睛】本题主要考查了一次函数和反比例函数的性质,解题的关键是熟练掌握一次函数和反比例函数的增减性.
5. 下列四个命题:①平行四边形的两组对角分别相等;②对角线互相垂直且平分的四边形是菱形;③矩形是轴对称图形;④对角线相等的菱形是正方形;其中真命题的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【分析】根据平行四边形、矩形的性质定理以及菱形、正方形的判定定理进行判断即可.
【详解】解:由题意知,平行四边形的两组对角分别相等是真命题,故①符合要求;
对角线互相垂直且平分的四边形是菱形是真命题;故②符合要求;
矩形是轴对称图形是真命题;故③符合要求;
对角线相等的菱形是正方形是真命题;故④符合要求;
∴真命题有4个,
故选:D.
【点睛】本题考查了平行四边形、矩形的性质定理以及菱形、正方形的判定定理,真命题等知识.解题的关键在于对知识的熟练掌握.
6. 如图,是的直径,若,连接,,则的度数是( )
A. B. C. D.
【答案】C
【分析】本题考查了圆心角的性质,圆的内接四边形互补,等边三角形的判定,解题的关键是求出.
【详解】解:如下图,连结,
,
,
,
,
故选:C.
二、填空题:本题共12小题,每小题4分,共48分.
7. 的相反数是_________________;
【答案】2
【分析】根据只有符号不同的两个数叫做互为相反数解答即可.
【详解】2的相反数是2.
故答案为2.
【点睛】本题考查了实数的性质,熟记概念与性质是解题的关键.
8. 在函数中,自变量x的取值范围为_______.
【答案】
【分析】本题考查了函数的取值范围,解题的关键是知晓分式有意义的条件.
根据函数中分式的分母不为0即可得到答案.
【详解】当分式的分母为零时,分式才没有意义,故.
即自变量x的取值范围为.
故答案为:.
9. 方程 =0的解是_______.
【答案】1
【分析】首先根据二次根式有意义的条件,判定x的取值范围,然后方程两边同时平方,解一元二次方程即可得解.
【详解】根据题意,得
解得
将方程两边平方,得
解得
综上,
【点睛】此题主要考查二次根式有意义的条件以及一元二次方程的求解,熟练掌握,即可解题.
10. 如果一个正多边形的中心角等于,那么这个正多边形的边数是______.
【答案】12
【分析】本题考查正多边形的中心角与边数之间的关系,根据正边形的中心角为,即可解题.
【详解】解:设这个正多边形的边数是,且一个正多边形的中心角等于,
有,解得,
故答案为:12.
11. 关于x的一元二次方程有两个不相等的实数根,则k的取值范围是______.
【答案】且
【分析】本题考查了根的判别式,根据方程的根的判别式且计算即可.
【详解】∵一元二次方程有两个不相等的实数根,
∴且,
解得且,
故答案为:且.
12. 在平面直角坐标系中,若反比例函数的图象位于第二、四象限,则k的取值范围是 _________.
【答案】
【分析】本题考查反比例函数的性质,解题的关键是掌握当时,的图象位于第二、四象限.根据反比例函数的性质列不等式即可解得答案.
【详解】解:反比例函数的图象位于第二、四象限,
,
解得,
故答案为:
13. 如图,电路图上有四个开关A,B,C,D和一个小灯泡,闭合开关D或同时闭合开关A,B,C,都可使小奵泡发光.现随机从A,B,C,D中抽取一个字母(每个字母被抽到的可能性相等)并闭合对应开关,则小灯泡发光的概率为__________.
【答案】
【分析】本题考查用概率公式计算事件发生的概率,熟练掌握概率公式:是解题的关键.
所有可能的结果共有4种可能,而让小灯泡发光的只有抽到D,一种可能,由概率公式即可求解.
【详解】解:小灯泡发光的概率为.
故答案为:.
14. 为了解某小区居民的用水情况,随机抽查了该小区10户家庭的月用水量,结果如下:
月用水量/t 10 13 14 17 18
户数 3 1 3 2 1
则这10户家庭月用水量的中位数是______.
【答案】14吨
【分析】本题考查了求中位数,正确理解中位数的定义是解题的关键.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.根据中位数的定义,即得答案.
【详解】将表中数据为从小到大排列,处在第5位、第6位的是14吨,
所以这10户家庭月用水量的中位数是14吨.
故答案为:14吨..
15. 如图,点是的重心,如果,,那么向量用向量和表示为______.
【答案】##
【分析】由是的重心,推出,,求出,可得结论.
【详解】解:∵G是的重心,
∴,,
∵,
∴,
故答案为:.
【点睛】本题考查三角形的重心,三角形法则等知识,解题的关键是掌握重心的性质,学会利用三角形法则解决问题.
16. 如图,点是直线上一动点,当线段最短时,的长为______.
【答案】
【分析】根据直线解析式求出点A、B的坐标,再根据勾股定理求出AB的长度,根据点到直线的所有线段中,垂线段最短,利用三角形的面积列式即可求解.
【详解】解:当时,,
当时,,
解得,
∴点A、B的坐标是,,
∴,
根据垂线段最短性质,时,最短,如点所示
此时,,
即,
解得,即.
故答案为:.
【点睛】本题综合考查了一次函数的问题,主要利用勾股定理,垂线段最短的性质,根据直线解析式求出点A、B的坐标是解题的关键.
17. 如图,以点O为圆心的两个同心圆,半径分别为5和3,若大圆的弦AB与小圆相交,则弦长AB的取值范围是 __.
【答案】
【分析】此题可以首先计算出当AB与小圆相切的时候的弦长.连接过切点的半径和大圆的一条半径,根据勾股定理和垂径定理,得AB=8.若大圆的弦AB与小圆有两个公共点,即相交,此时AB>8;又因为大圆最长的弦是直径10,则8<AB≤10.
【详解】解:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴.
当AB过圆心时最长即为大圆的直径10,
∴8<AB≤10.
故答案为:8<AB≤10.
【点睛】本题综合运用了切线的性质、勾股定理和垂径定理.此题可以首先计算出和小圆相切时的弦长,再进一步分析相交时的弦长.
18. 如图,矩形纸片中,,,折叠纸片,使点落在边上的点处,并且折痕交边于点,交边于点,把纸片展平,则线段长度的取值范围为______.
【答案】
【分析】设,则,当与重合时,证得即,进而利用勾股定理得,当与重合时,,即可得解.
【详解】解:设,则,
当与重合时,如下图,
∵四边形是矩形,
∴,,,
由折叠的性质可得,,
,
∴,
∴,
∴,
∴即,
解得,
∵,
∴即,
解得或(舍去),
当与重合时,如下图,
此时,
∴,
故答案为:.
【点睛】本题主要考查了勾股定理,相似三角形的判定及性质,折叠的性质,矩形的性质,熟练掌握矩形的性质及相似三角形的判定及性质是解题的关键.
三、解答题:本题共7小题,共78分.解答应写出文字说明,证明过程或演算步骤.
19. 计算;(-)-1+tan30°+|1-|-
【答案】-2-
【分析】直接利用绝对值的性质以及二次根式的性质、特殊角的三角函数值分别化简得出答案.
【详解】解:原式=-2+×+-1-2
=-2-.
【点睛】此题主要考查了实数运算,正确化简各数是解题关键.
20. 解不等式组:
【答案】
【分析】本题主要考查了解一元一次不等式组,先求出每个不等式的解集,再根据 “同大取大,同小取小,大小小大中间找,大大小小找不到(无解)”求出不等式组的解集即可.
【详解】解:
解不等式①,得,
解不等式②,得,
∴不等式组的解集为.
21. 如图,在中,,以点O为圆心,长为半径的圆交于点C,点D在边上,且.
(1)判断直线与的位置关系,并说明理由;
(2)若,求半径.
【答案】(1)直线与相切,理由见解析
(2)
【分析】本题考查了切线的证明、正切的应用等知识点,掌握相关几何结论是解题关键.
(1)连接,由得,结合,即可求解;
(2)设的半径为,可得,根据可得,即可求解;
【小问1详解】
解:直线与相切,理由如下:
连接,如图所示:
则
∴
∵
∴
∵
∴
∴
∵为半径,
∴直线与相切
【小问2详解】
解:设的半径为,
∵
∴,
∴
∵
∴,
解得:
22. 阅读理解:七年级一班数学学习兴趣小组在解决下列问题中,发现该类问题可以“建立直角坐标系、应用一次函数”解决问题.请先阅读下列解决问题的方法,然后再应用此方法解决后续问题.
问题:如图①,直立在点处的标杆长,站立在点处的观察者从点处看到标杆顶、旗杆顶在一条直线上.已知,,,求旗杆高.
解:建立如图②所示直角坐标系,则线段可看作一个一次函数的图象
由题意可得各点坐标为:点,,,且所求的高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得
∴
当时,,即.
解决问题:
请应用上述方法解决下列问题:
如图③,河对岸有一路灯杆,在灯光下,小明在点处测得自己的影长,沿方向到达点处再测得自己的影长.如果小明的身高为,求路灯杆
的高度.(参考:建立直角坐标系如图④)
【答案】
【分析】根据题中的例题过程连求两次一次函数解析式作答即可.
【详解】由题意可得各点坐标为:,,且所求的高度就为点的纵坐标.
设直线的函数关系式为.
把,代入得,解得.
∴直线的函数关系式为①.
∵直线过点,,
同理可得直线的解析式为②,
联立①②解得,,
答:路灯杆的高度.
【点睛】本题考查了求两直线的交点和对例题的理解应用能力,题目不难,但注意做题时需要运用题目所给方式做题而不能用其他的解答方法.
23. 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.
(1)求证:;
(2)如图2,连接AC交BD于O,连接OE,若CE⊥BC,求证:△POC∽△AEC.
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)根据菱形的性质,首先利用SAS证明△CDP≌△ADP,得PC=PA,∠DCP=∠DAP,再说明△PAE∽△PFA,得,即可证明结论;
(2)根据菱形的性质可说明∠COP=∠CEA,从而证明结论.
【小问1详解】
证明:∵四边形ABCD菱形,
∴AD=CD,∠CDP=∠ADP,,
在△CDP和△ADP中,
∴△CDP≌△ADP(SAS),
∴PC=PA,∠DCP=∠DAP,
∵,
∴∠DCP=∠F,
∴∠DAP=∠F,
∵∠APE=∠FPA,
∴△PAE∽△PFA,
∴,
∴PA2=PE PF,
∴PE PF=PC2;
【小问2详解】
∵CE⊥BC,
∴∠ECB=90°,
∵,
∴∠CEA=∠BCE=90°,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠COP=90°,
∴∠COP=∠CEA,
∵∠OCP=∠ECA,
∴△POC∽△AEC.
【点睛】本题主要考查了菱形的性质,相似三角形的判定与性质,全等三角形的判定与性质,证明PA=PC是解决问题(1)的关键.
24. 如图,直线y=﹣x+n与x轴交于点A(4,0),与y轴交于点B,抛物线y=﹣x2+bx+c经过点A,B.
(1)求抛物线解析式;
(2)E(m,0)为x轴上一动点,过点E作ED⊥x轴,交直线AB于点D,交抛物线于点P,连接BP.
①点E在线段OA上运动,若△BPD直角三角形,求点E的坐标;
②点E在x轴的正半轴上运动,若∠PBD+∠CBO=45°.请直接写出m的值.
【答案】(1)y=﹣x2+3x+4;(2)① E(2,0)或(3,0);②m=7或.
【分析】(1)将点A坐标代入直线解析式可求n的值,可求点B坐标,利用待定系数法可求解;
(2)①分两种情况讨论,勾股定理可求解;②分两种情况讨论,由相似三角形的性质和等腰三角形的性质,可求BP解析式,联立方程可求解.
【详解】解:(1)∵直线y=﹣x+n与x轴交于点A(4,0),
∴0=﹣4+n,
∴n=4,
∴直线解析式为:y=﹣x+4,
当x=0时,y=4,
∴点B(0,4),
∵抛物线y=﹣x2+bx+c经过点A,B,则,解得,
∴抛物线的解析式为:y=﹣x2+3x+4①;
(2)①∵ED⊥x轴,
∴∠PEA=90°,
∴∠BDP=∠ADE<90°,
设点E(m,0),点P(m,﹣m2+3m+4),则点D(m,﹣m+4),
∴PD2=(﹣m2+4m)2,BP2=m2+(﹣m2+3m)2,BD2=m2+(﹣m+4﹣4)2=2m2,
当∠PBD=90°时,BP2+BD2=PD2,
∴m2+(﹣m2+3m)2+2m2=(﹣m2+4m)2,
∴m=2,m=0(舍去)
∴点E的坐标为(2,0),
当∠BPD=90°时,BP2+PD2=BD2,
同理可得:m=0(舍去)或3或4(舍去),
∴点E的坐标为(3,0),
综上所述:点E的坐标为(2,0)或(3,0);
②当点P在x轴上方时,如图1,连接BC,延长BP交x轴于N,
∵点A(4,0),点B(0,4),
∴OA=OB=4,
∴∠BAO=∠ABO=45°,
∵抛物线y=﹣x2+3x+4与x轴交于点A,点C,
∴0=﹣x2+3x+4,
∴x1=4,x2=﹣1,
∴点C(﹣1,0),
∴OC=1,
∵∠PBD+∠CBO=45°,∠BAO=∠PBD+∠BNO=45°,
∴∠CBO=∠BNO,
又∵∠BOC=∠BON=90°,
∴△BCO∽△NBO,
∴,
∴,
∴ON=16,
∴点N(16,0),
∴直线BN解析式为:yx+4②,
联立①②并解得:x=0(舍去)或,
∴m;
当点P在x轴下方时,如图2,连接BC,设BP与x轴交于点H,
∵∠PBD+∠CBO=45°,∠OBH+∠PBD=45°,
∴∠CBO=∠OBH,
又∵OB=OB,∠COB=∠BOH,
∴△BOH≌△BOC(ASA),
∴OC=OH=1,
∴点H(1,0),
∴直线BH解析式为:y=﹣4x+4③,
联立①③并解得:x=0(舍去)或7,
∴点P的横坐标为7,
∴m=7,
综上所述:m=7或.
【点睛】本题是二次函数综合题,考查了二次函数的性质,待定系数法求解析式,相似三角形的判定和性质,全等三角形的判定和性质,勾股定理等知识,灵活运用这些性质解决问题是本题的关键.
25. 如图,已知菱形,对角线、相交于点,,.点从点A出发,以每秒4个单位的速度沿线段向点运动,同付,点从点出发,以每秒3个单位的速度沿折线向点运动,当点P、Q中有一个点达到终点时,两点同时停止运动.连接、、,设点的运动时间为秒.
(1)求线段的长;
(2)在整个运动过程中,能否成为直角三角形?若能,请求出符合题意的t的值;若不能,请说明理由;
(3)以为圆心,为半径作,当与线段只有一个公共点时,求的值或的取值范围.
【答案】(1)12 (2)能,或
(3)或
【分析】(1)首先根据四边形是菱形,可得,,,利用勾股定理即可求出.
(2)情形1:如图1中,当时,,利用得列出方程求解;情形2:如图2,当时,,作垂足为,利用得到列出方程即可解决.
(3)情形1:如图3,当点在线段上时,与线段相切于,连接,此时与线段只有一个交点,利用得到列出方程解决.
情形2:如图4,当时,作垂足为,由得到列出方程求解.
【小问1详解】
解: 四边形是菱形,
,,,
,
,
在中,,,
.
【小问2详解】
解:能.理由如下:
如图1,当时,,
,,
,
,
,
,
,
或不合题意舍弃)
.
如图2,当时,,作垂足为,
,
,
,
,,,,
,,
,
,
,
,
,
解得或不合题意舍弃)
综上所述或时是直角三角形.
【小问3详解】
解:①如图3,当点在线段上时,与线段相切于,连接,
此时与线段只有一个交点,
在中,,,
,
,,
,
,
,解得或不合题意舍弃).
②如图4,当时,作垂足为,
,,
,
,
,解得.
时与线段只有一个交点.
综上所述或时与线段只有一个交点.
【点睛】本题考查菱形的性质、勾股定理、相似三角形的判定和性质、圆的有关知识,学会分类讨论是解题的关键,解题中培养动手画图能力,利用转化的数学思想去思考问题.
同课章节目录
