2015-2016学年高一物理人教版必修1配套课件:第二章 第3讲 匀变速直线运动的位移与时间的关系(47张PPT)
文档属性
| 名称 | 2015-2016学年高一物理人教版必修1配套课件:第二章 第3讲 匀变速直线运动的位移与时间的关系(47张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 821.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-12-09 06:34:34 | ||
图片预览









文档简介
课件47张PPT。第二章——匀变速直线运动的研究第3讲 匀变速直线运动的位移与时间的关系目标定位
1.了解位移公式的推导过程,理解公式的含义,知道位移对应v-t图象与坐标轴围成的面积.
2.会利用公式x=v0t+ at2和匀变速直线运动的v-t图象解决有关问题.
3.了解匀速直线运动的x-t图象的意义、特点,了解匀变速直线运动的x-t图象的特点.预习导学 梳理·识记·点拨 一、匀速直线运动的位移
做匀速直线运动的物体在时间t内的位移x= ,在速度图象中,位移在数值上等于v-t图象与对应的时间轴所围的_____
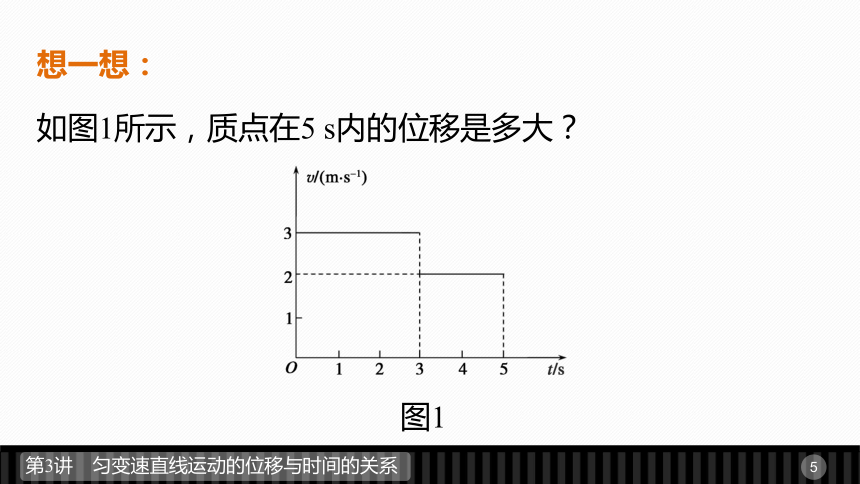
.vt矩形面积想一想:
如图1所示,质点在5 s内的位移是多大?图1答案 v-t图象中矩形的面积表示质点的位移,由图可知质点3秒内的位移为3×3 m=9 m,后2秒的位移为2×2 m=4 m,
5秒内的位移是9 m+4 m=13 m.二、匀变速直线运动的位移
1.由v-t图象求位移:
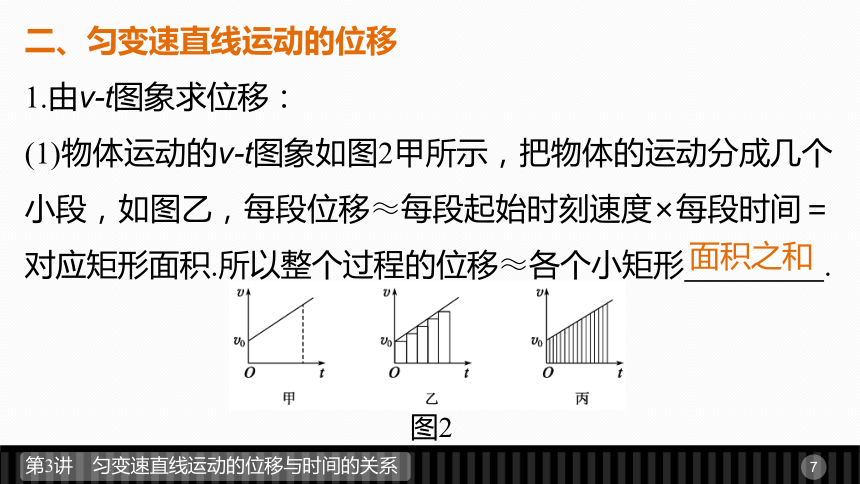
(1)物体运动的v-t图象如图2甲所示,把物体的运动分成几个小段,如图乙,每段位移≈每段起始时刻速度×每段时间=对应矩形面积.所以整个过程的位移≈各个小矩形 .图2面积之和(2)把运动分成更多的小段,如图丙,各小矩形的 ,
可以更精确地表示物体在整个过程的位移.
(3)把整个过程分得非常非常细,小矩形合在一起形成了一个梯形, 就代表物体在相应时间间隔内的位移.面积之和梯形的面积(4)结论:匀变速直线运动的v-t图象与t轴 代表匀变速直线运动相应时间内的位移.
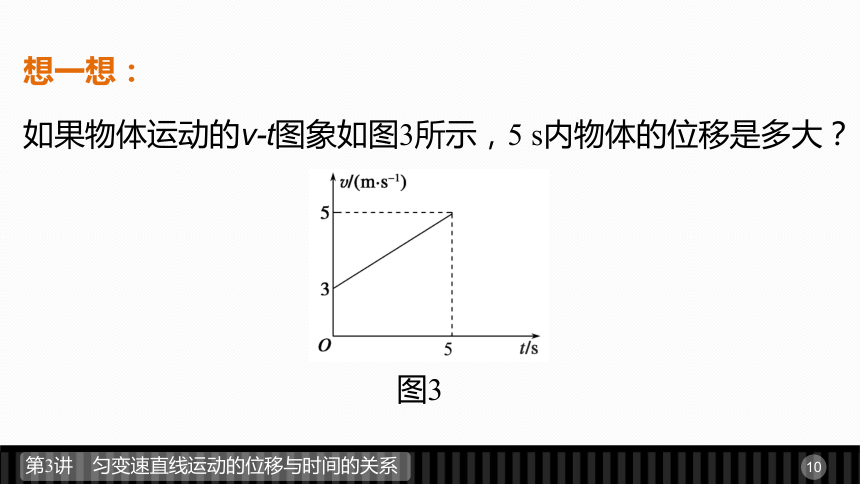
2.位移与时间关系式:x= .包围的面积想一想:
如果物体运动的v-t图象如图3所示,5 s内物体的位移是多大?图3答案 根据v-t图象与t轴所围的面积表示位移,可知物体
t 时间内的位移等于梯形的面积:x=S= m=
20 m.三、用图象表示位移(x-t 图象)
1.定义:以 为横坐标,以 为纵坐标,描述位移随时间变化情况的图象叫位移—时间图象.
2.静止物体的x-t图象:是一条 的直线.
3.匀速直线运动的x-t图象:是一条 的直线.时间位移平行于时间轴倾斜课堂讲义 理解·深化·探究一、匀变速直线运动的位移公式及有关计算
1.位移公式 x=v0t+ at2的推导
如图2所示,在匀变速直线运动中运用“无限分割、逐步逼近”的微分思想可得v-t图象与时间轴所围成的“面积”表示位移.如图4所示,速度图线和时间轴所包围的梯形面积为S=
(OC+AB)·OA.图42.对位移公式x=v0t+ at2的理解
(1)适用条件:匀变速直线运动.
(2)公式x=v0t+ at2为矢量式,其中的x、v0、a 都是矢量,应用时必须选取统一的正方向,一般选初速度v0的方向为正方向:
①匀加速直线运动,a取正值;匀减速直线运动,a取负值.②若位移为正值,位移的方向与规定的正方向相同;若位移为负值,位移的方向与规定的正方向相反.
(3)两种特殊形式:
①当a=0时,x=v0t(匀速直线运动).
②当v0=0时,x= at2(由静止开始的匀变速直线运动).3.用v-t图象求位移
图线与时间轴所围成的“面积”表示位移.“面积”在时间轴上方表示位移为正,在时间轴下方表示位移为负;通过的路程为时间轴上、下方“面积”绝对值之和.例1 一辆汽车以1 m/s2的加速度加速行驶了12 s,驶过了180 m,汽车开始加速时的速度为多少?
解析 以汽车初速度方向为正方向,运动示意图如图所示答案 9 m/s例2 物体由静止开始在水平面上行驶,0~6 s内的加速度随时间变化的图线如图5甲所示.图5(1)在图乙中画出物体在0~6 s内的v-t图线;
解析 第1秒内为初速度0的匀加速直线运动,末速度v1=at=4 m/s,v-t 图象是倾斜的直线,1~4 s加速度为0,速度不变为匀速直线运动,4~6 s初速度为第1秒的末速度v1=4 m/s,加速度a′=-2 m/s2,末速度v6=v1+a′t=0,图象如图所示:答案 见解析图(2)求在这6 s内物体的位移.答案 18 m二、位移-时间图象(x-t图象)
1.对x-t图象的理解
(1)斜率:斜率的绝对值表示速度的大小;斜率的正负表示速度的方向.
(2)截距:纵截距表示物体起始位置,横截距表示物体开始运动的时刻.
(3)交点:交点表示两物体在同一时刻处于同一位置,即相遇.2.几种常见的位移-时间图象
(1)静止物体的x-t图象是平行于时间轴的直线,如图6直线a.
(2)匀速直线运动的x-t图象是一条倾斜的直线,如图直线b,斜率表示速度.(3)匀变速直线运动的x-t图象是抛物线,如图曲线c,曲线上某点切线的斜率表示那一时刻的速度.图63.注意:(1)无论是v-t图象还是x-t图象都不是物体的运动轨迹.
(2)v-t图象和x-t图象都只能描述直线运动,不能描述曲线运动.例3 如图7是在同一条直线上运动的A、B两质点的x-t图象,由图可知( )
A.t=0时,A在B后面
B.B质点在t2秒末追上A并在此后跑在
A的前面
C.在0~t1时间内B的运动速度比A大图7D.A质点在0~t1做加速运动,之后做匀速运动
解析 由图象可知,t=0时,B在A后面,故A不对;
B质点在t2秒末追上A并在此后跑在A的前面,B正确;
在0~t1时间内B的斜率小于A,故B的运动速度比A小,C不对;
A质点在0~t1做匀速运动,故D不对.
答案 B三、刹车类问题
实际交通工具刹车后可认为是做匀减速直线运动,当速度减小到零时,车辆就会停止.解答此类问题的思路是:先求出它们从刹车到静止的刹车时间 ,再比较所给时间与刹车时间的关系确定运动时间,最后再利用运动学公式求解.注意:对于末速度为零的匀减速直线运动,也可采用逆向思维法,即把运动倒过来看成是初速度为零的匀加速直线运动.例4 一辆汽车以108 km/h的速度行驶,现因紧急事故急刹车并最终停止运动.已知汽车刹车过程的加速度大小为6 m/s2,则从开始刹车经过7 s汽车通过的距离是多少?
解析 设从刹车开始至汽车停止所用的时间为t0,选v0的方向为正方向.方法一:因为汽车刹车时间为5 s,之后汽车是静止的.故刹车7 s内通过的距离等于刹车5 s内经过的位移,答案 75 m对点练习 巩固·应用·反馈匀变速直线运动的位移及有关计算
1.某质点的位移随时间变化的关系是x=4t+4t2,x与t的单位分别为m和s,下列说法正确的是( )
A.v0=4 m/s,a=4 m/s2 B.v0=4 m/s,a=8 m/s2
C.2 s内的位移为24 m D.2 s末的速度为24 m/s解析 将位移随时间变化的关系与位移公式x=v0t+ at2相对照即可判定v0=4 m/s,a=8 m/s2,A错误,B正确.
把t=2 s代入公式可得x=24 m,C正确.
由于v=v0+at,即v=4+8t,把t=2 s代入可得v=20 m/s,D错误.
答案 BC2.某物体运动的v-t图象如图8所示,根据图象可知,该物体( )
A.在0到2 s末的时间内,加速度为1 m/s2
B.在0到5 s末的时间内,位移为10 m
C.在0到6 s末的时间内,位移为7.5 m
D.在0到6 s末的时间内,位移为6.5 m图8在 5~6 s内物体的位移等于t轴下面三角形面积x2=-( ×1
×1) m=-0.5 m,故0~6 s内物体的位移x=x1+x2=6.5 m,D正确,C错误.答案 AD位移-时间图象(x-t图象)
3.甲、乙两质点同时开始做直线运动,它们的位移x与时间t 的图象如图9所示,则( )
A.甲物体做匀加速直线运动,乙物体做曲线
运动
B.甲、乙两物体从同一地点出发图9C.出发时乙在甲前x0处
D.甲、乙两物体有两次相遇
解析 由于图象是x-t图象,过原点的直线表示物体做匀速直线运动,所以甲做匀速直线运动,A不对;
甲从原点出发,乙从x0处出发,故B不对、C对;由图看出,甲、乙有两个交点,故两物体有两次相遇,D是正确的.
答案 CD刹车类问题
4.一辆卡车紧急刹车过程加速度的大小是5 m/s2,如果在刚刹车时卡车的速度为10 m/s,求:
(1)刹车开始后1 s内的位移大小;答案 7.5 m (2)刹车开始后3 s内的位移大小和3 s内的平均速度大小.t2=3 s的位移大小等于前2 s内的位移大小
1.了解位移公式的推导过程,理解公式的含义,知道位移对应v-t图象与坐标轴围成的面积.
2.会利用公式x=v0t+ at2和匀变速直线运动的v-t图象解决有关问题.
3.了解匀速直线运动的x-t图象的意义、特点,了解匀变速直线运动的x-t图象的特点.预习导学 梳理·识记·点拨 一、匀速直线运动的位移
做匀速直线运动的物体在时间t内的位移x= ,在速度图象中,位移在数值上等于v-t图象与对应的时间轴所围的_____
.vt矩形面积想一想:
如图1所示,质点在5 s内的位移是多大?图1答案 v-t图象中矩形的面积表示质点的位移,由图可知质点3秒内的位移为3×3 m=9 m,后2秒的位移为2×2 m=4 m,
5秒内的位移是9 m+4 m=13 m.二、匀变速直线运动的位移
1.由v-t图象求位移:
(1)物体运动的v-t图象如图2甲所示,把物体的运动分成几个小段,如图乙,每段位移≈每段起始时刻速度×每段时间=对应矩形面积.所以整个过程的位移≈各个小矩形 .图2面积之和(2)把运动分成更多的小段,如图丙,各小矩形的 ,
可以更精确地表示物体在整个过程的位移.
(3)把整个过程分得非常非常细,小矩形合在一起形成了一个梯形, 就代表物体在相应时间间隔内的位移.面积之和梯形的面积(4)结论:匀变速直线运动的v-t图象与t轴 代表匀变速直线运动相应时间内的位移.
2.位移与时间关系式:x= .包围的面积想一想:
如果物体运动的v-t图象如图3所示,5 s内物体的位移是多大?图3答案 根据v-t图象与t轴所围的面积表示位移,可知物体
t 时间内的位移等于梯形的面积:x=S= m=
20 m.三、用图象表示位移(x-t 图象)
1.定义:以 为横坐标,以 为纵坐标,描述位移随时间变化情况的图象叫位移—时间图象.
2.静止物体的x-t图象:是一条 的直线.
3.匀速直线运动的x-t图象:是一条 的直线.时间位移平行于时间轴倾斜课堂讲义 理解·深化·探究一、匀变速直线运动的位移公式及有关计算
1.位移公式 x=v0t+ at2的推导
如图2所示,在匀变速直线运动中运用“无限分割、逐步逼近”的微分思想可得v-t图象与时间轴所围成的“面积”表示位移.如图4所示,速度图线和时间轴所包围的梯形面积为S=
(OC+AB)·OA.图42.对位移公式x=v0t+ at2的理解
(1)适用条件:匀变速直线运动.
(2)公式x=v0t+ at2为矢量式,其中的x、v0、a 都是矢量,应用时必须选取统一的正方向,一般选初速度v0的方向为正方向:
①匀加速直线运动,a取正值;匀减速直线运动,a取负值.②若位移为正值,位移的方向与规定的正方向相同;若位移为负值,位移的方向与规定的正方向相反.
(3)两种特殊形式:
①当a=0时,x=v0t(匀速直线运动).
②当v0=0时,x= at2(由静止开始的匀变速直线运动).3.用v-t图象求位移
图线与时间轴所围成的“面积”表示位移.“面积”在时间轴上方表示位移为正,在时间轴下方表示位移为负;通过的路程为时间轴上、下方“面积”绝对值之和.例1 一辆汽车以1 m/s2的加速度加速行驶了12 s,驶过了180 m,汽车开始加速时的速度为多少?
解析 以汽车初速度方向为正方向,运动示意图如图所示答案 9 m/s例2 物体由静止开始在水平面上行驶,0~6 s内的加速度随时间变化的图线如图5甲所示.图5(1)在图乙中画出物体在0~6 s内的v-t图线;
解析 第1秒内为初速度0的匀加速直线运动,末速度v1=at=4 m/s,v-t 图象是倾斜的直线,1~4 s加速度为0,速度不变为匀速直线运动,4~6 s初速度为第1秒的末速度v1=4 m/s,加速度a′=-2 m/s2,末速度v6=v1+a′t=0,图象如图所示:答案 见解析图(2)求在这6 s内物体的位移.答案 18 m二、位移-时间图象(x-t图象)
1.对x-t图象的理解
(1)斜率:斜率的绝对值表示速度的大小;斜率的正负表示速度的方向.
(2)截距:纵截距表示物体起始位置,横截距表示物体开始运动的时刻.
(3)交点:交点表示两物体在同一时刻处于同一位置,即相遇.2.几种常见的位移-时间图象
(1)静止物体的x-t图象是平行于时间轴的直线,如图6直线a.
(2)匀速直线运动的x-t图象是一条倾斜的直线,如图直线b,斜率表示速度.(3)匀变速直线运动的x-t图象是抛物线,如图曲线c,曲线上某点切线的斜率表示那一时刻的速度.图63.注意:(1)无论是v-t图象还是x-t图象都不是物体的运动轨迹.
(2)v-t图象和x-t图象都只能描述直线运动,不能描述曲线运动.例3 如图7是在同一条直线上运动的A、B两质点的x-t图象,由图可知( )
A.t=0时,A在B后面
B.B质点在t2秒末追上A并在此后跑在
A的前面
C.在0~t1时间内B的运动速度比A大图7D.A质点在0~t1做加速运动,之后做匀速运动
解析 由图象可知,t=0时,B在A后面,故A不对;
B质点在t2秒末追上A并在此后跑在A的前面,B正确;
在0~t1时间内B的斜率小于A,故B的运动速度比A小,C不对;
A质点在0~t1做匀速运动,故D不对.
答案 B三、刹车类问题
实际交通工具刹车后可认为是做匀减速直线运动,当速度减小到零时,车辆就会停止.解答此类问题的思路是:先求出它们从刹车到静止的刹车时间 ,再比较所给时间与刹车时间的关系确定运动时间,最后再利用运动学公式求解.注意:对于末速度为零的匀减速直线运动,也可采用逆向思维法,即把运动倒过来看成是初速度为零的匀加速直线运动.例4 一辆汽车以108 km/h的速度行驶,现因紧急事故急刹车并最终停止运动.已知汽车刹车过程的加速度大小为6 m/s2,则从开始刹车经过7 s汽车通过的距离是多少?
解析 设从刹车开始至汽车停止所用的时间为t0,选v0的方向为正方向.方法一:因为汽车刹车时间为5 s,之后汽车是静止的.故刹车7 s内通过的距离等于刹车5 s内经过的位移,答案 75 m对点练习 巩固·应用·反馈匀变速直线运动的位移及有关计算
1.某质点的位移随时间变化的关系是x=4t+4t2,x与t的单位分别为m和s,下列说法正确的是( )
A.v0=4 m/s,a=4 m/s2 B.v0=4 m/s,a=8 m/s2
C.2 s内的位移为24 m D.2 s末的速度为24 m/s解析 将位移随时间变化的关系与位移公式x=v0t+ at2相对照即可判定v0=4 m/s,a=8 m/s2,A错误,B正确.
把t=2 s代入公式可得x=24 m,C正确.
由于v=v0+at,即v=4+8t,把t=2 s代入可得v=20 m/s,D错误.
答案 BC2.某物体运动的v-t图象如图8所示,根据图象可知,该物体( )
A.在0到2 s末的时间内,加速度为1 m/s2
B.在0到5 s末的时间内,位移为10 m
C.在0到6 s末的时间内,位移为7.5 m
D.在0到6 s末的时间内,位移为6.5 m图8在 5~6 s内物体的位移等于t轴下面三角形面积x2=-( ×1
×1) m=-0.5 m,故0~6 s内物体的位移x=x1+x2=6.5 m,D正确,C错误.答案 AD位移-时间图象(x-t图象)
3.甲、乙两质点同时开始做直线运动,它们的位移x与时间t 的图象如图9所示,则( )
A.甲物体做匀加速直线运动,乙物体做曲线
运动
B.甲、乙两物体从同一地点出发图9C.出发时乙在甲前x0处
D.甲、乙两物体有两次相遇
解析 由于图象是x-t图象,过原点的直线表示物体做匀速直线运动,所以甲做匀速直线运动,A不对;
甲从原点出发,乙从x0处出发,故B不对、C对;由图看出,甲、乙有两个交点,故两物体有两次相遇,D是正确的.
答案 CD刹车类问题
4.一辆卡车紧急刹车过程加速度的大小是5 m/s2,如果在刚刹车时卡车的速度为10 m/s,求:
(1)刹车开始后1 s内的位移大小;答案 7.5 m (2)刹车开始后3 s内的位移大小和3 s内的平均速度大小.t2=3 s的位移大小等于前2 s内的位移大小
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
