六年级数学上册试题 第1章《数的整除》单元复习题 -沪教版(含解析)
文档属性
| 名称 | 六年级数学上册试题 第1章《数的整除》单元复习题 -沪教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 575.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览




文档简介
第1章《数的整除》单元复习题
一、单选题
1.下列说法中正确的是( )
①能够除尽的算式,被除数一定能被除数整除
②最小的素数是
③合数一定是偶数
④没有最大的素数
A.①、② B.②、③ C.②、④ D.③、④
2.下面四个数都是六位数,N为非0且比10小的自然数,S是0,一定能被3和5整除的数是( )
A. B. C. D.
3.正整数N的各个数位上的数字之积为20,则下列哪一项不可能是的各个数位上数字的乘积( )
A.35 B.25 C.40 D.30 E.24
4.有一个三位数,百位数字是最小的奇数,十位上是0,个位上是一位数中最大的偶数.这个数是( )
A.102 B.201 C.801 D.108
5.下列说法错误的是( ).
A.负整数和自然数统称为整数
B.数a能被数b除尽,则数a一定能被数b整除
C.一个大于1的整数,至少能被两个数整除
D.在10以内只能被两个数整除的最大数是7
6.若a、b为正整数,且,则下列何者不可能为a、b的最大公因数?( )
A.1 B.6 C.8 D.12
7.下列说法:①,n一定能整除m;②24和36公有的素因数是2,3;③整数a的最大因数正好等于整数b的最小倍数,则a一定大于b;④因为,所以6.3是7的倍数,错误的个数是( )
A.1个 B.2个 C.3个 D.4个
8.一筐苹果,平均分给2个小朋友或3个小朋友或4个小朋友或5个小朋友,都正好分完,这筐苹果最少应有( )
A.60个 B.120个 C.900个 D.30个
9.我国数学家陈景润证明:任何充分大的偶数可以写成一个质数加上不超过两个质数的乘积的形式例如:,,那么( )
A. B. C. D.
10.x是正整数,表示不超过x的素数的个数.如:,不超过7的素数有2、3、5、7共4个,那么的值是( )
A.9 B.10 C.11 D.12
二、填空题
11.,都是整数,大于,且,那么的最大值为( ),最小值为( ).
12.一列数1,1,2,3,5,8,13,21,…,从第三项开始每一项是前两项的和,第2021个数是 数(填“奇”或“偶”);第2021个数除以3的余数是 .
13.一个三位数,被17除余5,被18除余12,那么它可能是 ;一个四位数,被131除余112,被132除余98,那么它可能是 ;
14.已知甲乙丙三个数,甲和乙的最大公约数是12,甲和丙的最大公约数是15,而三个数的最小公倍数是120,则甲、乙、丙三个数分别是 .
15.一个五位数能被3整除,且能被2整除,这样的五位数有 个.
16.m是小于400的奇数,m名学生排成一排,自左到右报数三次,第一次从1到3报数,第二次从1到7报数,第三次从1到11报数.如果位于中间的三名学生从左到右依次报了3、7、11,那么 .
17.某汽车公司同时建成两条生产线,第一条生产线第一个月生产了1000辆汽车,以后每个月比前一个月多生产100辆;第二条生产线第一个月的前半个月与后半个月各生产了500辆汽车,以后每半个月比前半个月多生产50辆,那么,这两条生产线共生产20000辆汽车需 个月.
18.桌上放有多于4堆的糖块,每堆数量均不相同,而且都是不大于100的质数,其中任意三堆糖块可以平分给三位小朋友,任意四堆糖块可以平分给四位小朋友,已知其中有一堆是17块糖,则这桌子上放的糖块最多的一堆是 块.
三、解答题
19.计算
(1) (2)
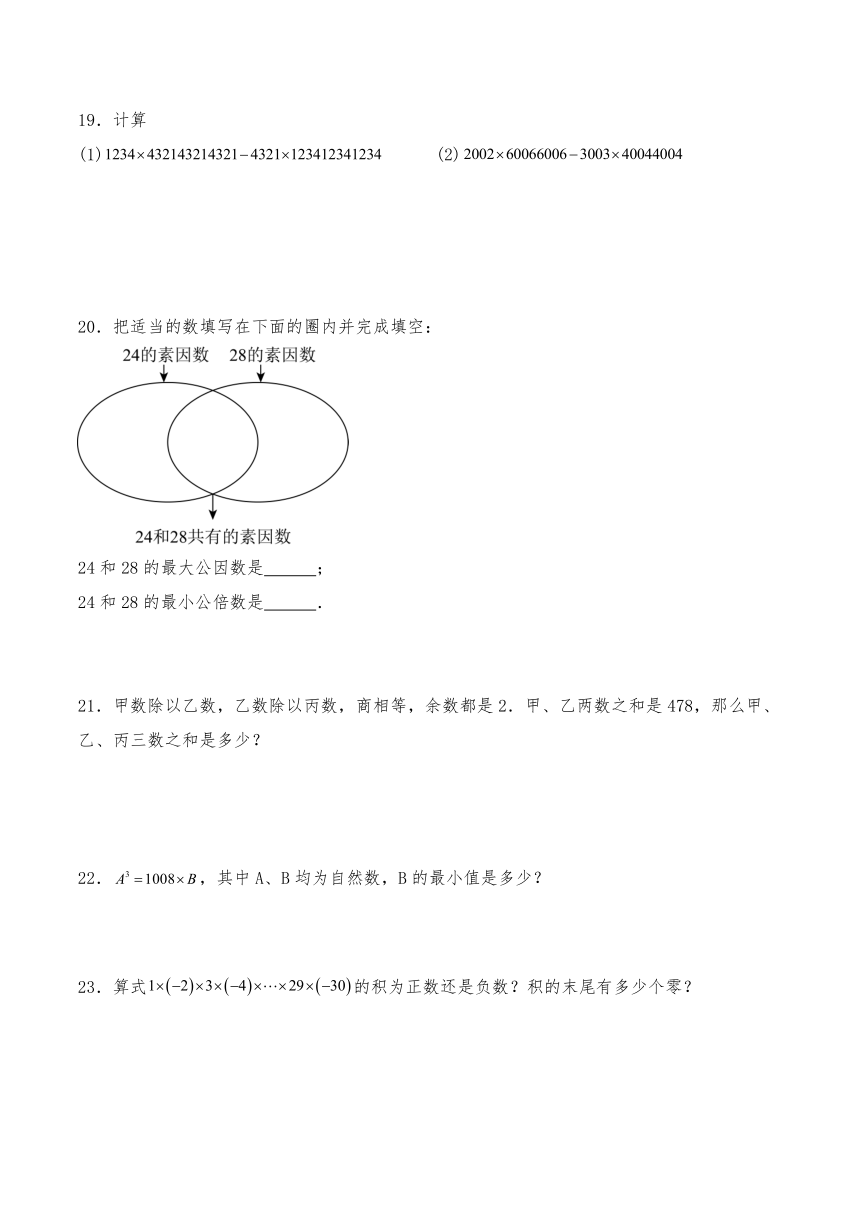
20.把适当的数填写在下面的圈内并完成填空:
24和28的最大公因数是 ;
24和28的最小公倍数是 .
21.甲数除以乙数,乙数除以丙数,商相等,余数都是2.甲、乙两数之和是478,那么甲、乙、丙三数之和是多少?
22.,其中A、B均为自然数,B的最小值是多少?
23.算式的积为正数还是负数?积的末尾有多少个零?
24.在欢庆中华人民共和国成立七十周年之际,学校在一块长80米,宽24米的长方形绿地四周插上彩旗,长方形的四个角各插一面彩旗,并且要求相邻两面彩旗间的距离相等.
(1)在各个方案中,相邻两面彩旗之间最大距离是多少米?
(2)在所有方案中,至少要在绿地四周插多少面彩旗?
25.某校预初年级开展了古诗文大赛,设有一、二、三等奖.其中获得一等奖的人数占参赛人数的,获得二等奖的人数占参赛人数的,获得三等奖的人数占参赛人数的.已知该年级共有学生400人.
(1)求这次评选参赛的同学有多少名?
(2)求这次评选获得一等奖的同学有多少名?
26.一个两位数的十位上的数为a,个位上的数为b,这个两位数记作;一个三位数的百位上的数为x,十位上的数为y,个位上的数为z,这个三位数记作.
(1)(+)能被11整除吗?请说明理由;
(2)小明发现:如果能被3整除, 那么就能被3整除.请补全小明的证明思路.
27.阅读材料:的末尾数字是3,的末尾数字是9,的末尾数字是7,的末尾数字是1,的末尾数字是3,......,观察规律,,∵的末尾数字是1,∴的末尾数字是1,∴的末尾数字是3,同理可知,的末尾数字是9,的末尾数字是7.解答下列问题:
(1)的末尾数字是 ,的末尾数字是 ;
(2)求的末尾数字;
(3)求证:能被5整除.
答案
一、单选题
1.C
【分析】利用整除的定义、素数定义及合数定义判断即可
【解析】解:能够除尽的算式,商为整数,叫做被除数能被除数整除,故①错误;
最小的素数是,故②正确;
合数不一定是偶数,例如:是合数但是不是偶数,故③错误;
没有最大的素数,故④正确,
故选:C
2.B
【分析】根据能被3和5整除的数的特点,进行判断即可.
【解析】解:A.,尾数不一定是0,5,不一定能被5整除,不符合题意;
B.,尾数为0,一定能被5整除,也一定能被整除,符合题意;
C.,尾数为0,一定能被5整除,不一定能被3整除,不符合题意;
D.尾数不一定是0,5,不一定能被5整除,不符合题意;
故选B.
3.A
【分析】根据,可知,当正整数为两位数时,为或,当正整数为三位或三位以上数时,有两种情况,一种是有一个数位上的数字为4,一个数位上的数字为5,剩余数位上的数字均为1,第二种是有2个数位上的数字为2,一个数位上的数字为5,当是四位或四位以上时,剩余数位上的数字均为1,逐一进行分析即可得出结论.
【解析】解:因为,所以当正整数为两位数时,为或,或,的各个数位上数字的乘积为或;
当正整数为三位或三位以上数时:
①有一个数位上的数字为4,一个数位上的数字为5,剩余数位上的数字均为1,当尾数为1时,的尾数变为2,的各个数位上数字的乘积为:;当尾数为5时,的尾数变为6,的各个数位上数字的乘积为:;当尾数为4时,的尾数变为5,的各个数位上数字的乘积为:;
②有2个数位上的数字为2,一个数位上的数字为5,当为四位或四位以上时,剩余数位上的数字均为1,当尾数为1时,的尾数变为2,的各个数位上数字的乘积为:;当尾数为2时,的尾数变为3,的各个数位上数字的乘积为:;当尾数为5时,的尾数变为6,的各个数位上数字的乘积为:;
综上:的各个数位上数字的乘积可能为:;故均有可能,不符合题意;不可能,符合题意;
故选A.
4.D
【分析】最小的奇数为1一位数中最大的偶数为8,代入三位数中即可求解.
【解析】最小的奇数为1,所以百位数为1
一位数中最大的偶数为8,所以个位数为8
所以这个百位数是108
故答案为D.
5.B
【分析】根据整数、整除的性质分析,即可得到答案.
【解析】∵数a能被数b除尽,结果可能是整数,也可能是分数
∴数a不一定能被数b整除
∴选项B错误;
又∵其他选项均正确
故选:B.
6.C
【分析】根据,取a、b的不同值解题即可.
【解析】解:最大公因数为a、b都有的因数,
而,,
a、b不可能都含有,
不可能为a、b的最大公因数.
故选:C.
7.D
【分析】根据整除的定义可对①进行判断;分别找出24和36的素因数,得出公有的素因数可对②进行判断;根据一个整数的最大因数是它本身,一个整数的最小倍数是它本身可对③进行判断;根据整除的定义可对④进行判断;综上即可得答案.
【解析】,不能确定m、n是整数,故①错误,
24=2×2×2×3,
36=2×2×3×3,
∴24和36公有的素因数是2、2、3,故②错误,
∵一个整数的最大因数是它本身,一个整数的最小倍数是它本身,
∴整数a的最大因数正好等于整数b的最小倍数,则a=b;故③错误,
是除进不是整除,故④错误,
综上所述:错误的有①②③④,共4个,
故选:D.
8.A
【分析】要求这框苹果最少有多少个,即要求2,3,4,5的最小公倍数.
【解析】因为2,3,4和5的最小公倍数是:,
所以这筐苹果最少应有60个.
故选:A.
9.C
【分析】根据“1+2”定理:一个偶数=一个质数+一个质数×一个质数,选出符合题意的算式即可.
【解析】解析:,9是合数,所以不符合题意;
,所以不符合题意;
,三个数都是素数,符合题意;
,1不是质数,77是合数,所以不符合题意,
故选C.
10.C
【分析】根据题意所给定义新运算及素数与合数的概念直接进行求解.
【解析】解:表示不超过23的素数有2、3、5、7、11、13、17、19、23共九个,则;
表示不超过95的素数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89共24个,则有,
由可得;
;
故选C.
二、填空题
11. 2008 8
【分析】都是2009的因数,先找出2009的所有因数,要使得最大,那么取最大的因数2009,取最小因数1即可;求的最小值,则两个因数最接近即可.
【解析】解:因为,都是整数,大于,,
所以的最大值为,最小值为,
故答案为:2008,8.
12. 奇 2
【分析】这个数列从左到右每3个数为一组,每一组循环中前两个是奇数,第三个为偶数,,余数是2,余下的这个数是奇数;由题意知:这串数的规律是1、1、2、3、5、8…,从第三个数是前面两个数的和,分别计算这些数除以3的余数,找出规律:每8个为一循环,用2021除以8,看看有多少个循环,余数是几则看循环数里第几个数,是几就余几.
【解析】∵,
∴余数是2,所以余下的这个数是奇数;
∵一串数是:1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987…,
∴这些数除以3余数是1、1、2、0、2、2、1、0、1、1、2、0、2、2、1、0…,
∴余数中每8个为一循环,循环1、1、2、0、2、2、1、0,
∵,
∴这串数的第2021个数除以3的余数是2.
故答案为:奇,2.
13. 192,498,804 1946
【分析】设此三位数为,可得一定能被17整除,据此求出b的值即可;
设此四位数为,可得一定能被131整除,据此求出y的值即可.
【解析】设此三位数为, 可得到,所以一定能被17整除,,27,44.
这个三位数为192,498,804.
设此四位数为,可得到,所以一定能被131整除,,145(太大),
这个四位数是1946.
故答案为:192,498,804;1946
14.60,24,15或120,12,15
【分析】根据题意得甲是60或120,然后将120分解质因数,分情况讨论即可.
【解析】解:根据题意得:甲的因数有12也有15,那么甲最小是12与15的最小公倍数,即甲最小是60,又因为三个数最小公倍数是120,所以甲一定是120的因数,
∴甲是60或120,
把他们的最小公倍数120分解质因数,
,
当甲是60时 ,
所以丙为,
乙为 ,
当甲为120时,乙为 ,
丙为,
∴甲乙丙分别为 60,24,15或120,12,15.
15.16
【分析】根据能够被2整除的数的个位为偶数,先确定个位数,再根据能够被3整除的数的特征确定A,B即可.
【解析】解:能被2整除,则为0、2、4、6、8;
能被3整除,则能
被3整除.当时,A可为1、4、7;
当时,A可为2、5、8;
当时,A可为0、3、6、9;
当时,A可为1、4、7;
当时,A可为2、5、8;
所以这样的五位数有16个.
故答案为:16
16.
【分析】设位于中间的三名学生是第n名,名,名,由题意可知n能被3整除,能被7整除,能被11整除,先找出最小的两个连续自然数分别能被7和11整除,确定出前面的连续自然数,再加上7和11的最小公倍数使得结果能被3整除即可得到这三个连续自然数中最小的自然数,然后可得答案.
【解析】解:设位于中间的三名学生是第n名,名,名,则,
由题意得:n能被3整除,能被7整除,能被11整除,
分别能被7和11整除的两个连续自然数为21和22,前面的连续自然数是20,
7和11的最小公倍数是77,考虑20加上77的整数倍,使得结果能被3整除,
当时,97不能被3整数,不符合题意;
当时,174能被3整数,符合题意,
所以位于中间的三名学生是第174名,175名,176名,
所以,
故答案为:.
17.7.
18.89
【分析】各堆糖块数被3除都余2,被4除余1,则每堆糖块的数量都是块且是不大于100的质数,这些质数只有5,17,29,41,53,89,据此即可求解.
【解析】解:因为任意3堆数量之和能被3整除,所以每堆被3除的余数相同,又因为17被3除余2,所以各堆糖块数被3除都余2;同理,各堆糖块数被4除余1,所以每堆糖块的数量都是块,且是小于100的质数,这些质数只有5,17,29,41,53,89,
即这桌子上放的糖块最多的一堆是89,
故答案为:89.
三、解答题
19.(1)
(2)
20.解:如图所示:
∵24=2×2×2×3,
∴24 和 28 的最大公因数:4;
24 和 28 的最小公倍数:168.
21.解:由“余数是2,甲、乙两数之和是478”,因此是乙的倍数,因为,
甲数除以乙数,乙数除以丙数,商相等,余数都是2,则剔除商比乙大或商小于3的组合.
容易得到:(,,),
则甲、乙、丙三数之和:;
同理:(,,),
甲、乙、丙三数之和为:;
(,,),
甲、乙、丙三数之和为:.
答:甲、乙、丙三数之和是或或.
22.解:因为,
所以,
所以,
所以.
23.解:由题意知,算式中有15个负数,所以根据有理数的乘法法则,积为负数;
又5与任何一个偶数相乘的得数末尾必为0,且在1-30的30个数里面末尾为5的数有5,15,25,
∴5,15与偶数乘,各得1个0,25与4乘可得2个0,又10、20、30各有1个0,
所以,积的末尾共有7个0.
24.(1)解:∵,,
∴80与24的最大公因数是8,
∵相邻两面彩旗间的距离相等,
∴即相邻两面彩旗间最大距离是8米;
(2)解:要使得使用的彩旗数量最少,则要求相邻两面彩旗之间的距离最大,
根据(1)结果可知相邻两面彩旗间最大距离是8米,
即:,,
∴长方形的长边植树11棵,宽边植树4棵,
∴则总的彩旗数量为:(面).
答:至少在绿地四周插26面彩旗.
25.(1)∵,
∴、、的最小公倍数是,
答:这次评选参赛的同学有名;
(2)由(1)可知这次评选参赛的同学有名,
∴评选获得一等奖的同学有名,
答:这次评选获得一等奖的同学有名.
26.(1)解:能被整除,理由为:
,
∴能被整除.
(2)解:
,
∵,都能被3整除,
∴就能被3整除,
故答案为:,.
27.(1)解:,
的末尾数字为3;
的末尾数字是4,的末尾数字是6,的末尾数字是4,…
的末尾数字是4,的末尾数字是6,
的末尾数字是6;
故答案为:3,6;
(2)解:,
∵的末尾数字是6,
∴的末尾数字是4;
(3)证明:∵的末尾数字是2,的末尾数字是4,的末尾数字是8,的末尾数字是6,的末尾数字是2,…
的末尾数字是2,的末尾数字是4,的末尾数字是8,的末尾数字是6,
的末尾数字为6;
同理可得:
的末尾数字7,的末尾数字9,的末尾数字3,的末尾数字1;
的末尾数字9,
∴的末尾数字是5,
∴能被5整除.
一、单选题
1.下列说法中正确的是( )
①能够除尽的算式,被除数一定能被除数整除
②最小的素数是
③合数一定是偶数
④没有最大的素数
A.①、② B.②、③ C.②、④ D.③、④
2.下面四个数都是六位数,N为非0且比10小的自然数,S是0,一定能被3和5整除的数是( )
A. B. C. D.
3.正整数N的各个数位上的数字之积为20,则下列哪一项不可能是的各个数位上数字的乘积( )
A.35 B.25 C.40 D.30 E.24
4.有一个三位数,百位数字是最小的奇数,十位上是0,个位上是一位数中最大的偶数.这个数是( )
A.102 B.201 C.801 D.108
5.下列说法错误的是( ).
A.负整数和自然数统称为整数
B.数a能被数b除尽,则数a一定能被数b整除
C.一个大于1的整数,至少能被两个数整除
D.在10以内只能被两个数整除的最大数是7
6.若a、b为正整数,且,则下列何者不可能为a、b的最大公因数?( )
A.1 B.6 C.8 D.12
7.下列说法:①,n一定能整除m;②24和36公有的素因数是2,3;③整数a的最大因数正好等于整数b的最小倍数,则a一定大于b;④因为,所以6.3是7的倍数,错误的个数是( )
A.1个 B.2个 C.3个 D.4个
8.一筐苹果,平均分给2个小朋友或3个小朋友或4个小朋友或5个小朋友,都正好分完,这筐苹果最少应有( )
A.60个 B.120个 C.900个 D.30个
9.我国数学家陈景润证明:任何充分大的偶数可以写成一个质数加上不超过两个质数的乘积的形式例如:,,那么( )
A. B. C. D.
10.x是正整数,表示不超过x的素数的个数.如:,不超过7的素数有2、3、5、7共4个,那么的值是( )
A.9 B.10 C.11 D.12
二、填空题
11.,都是整数,大于,且,那么的最大值为( ),最小值为( ).
12.一列数1,1,2,3,5,8,13,21,…,从第三项开始每一项是前两项的和,第2021个数是 数(填“奇”或“偶”);第2021个数除以3的余数是 .
13.一个三位数,被17除余5,被18除余12,那么它可能是 ;一个四位数,被131除余112,被132除余98,那么它可能是 ;
14.已知甲乙丙三个数,甲和乙的最大公约数是12,甲和丙的最大公约数是15,而三个数的最小公倍数是120,则甲、乙、丙三个数分别是 .
15.一个五位数能被3整除,且能被2整除,这样的五位数有 个.
16.m是小于400的奇数,m名学生排成一排,自左到右报数三次,第一次从1到3报数,第二次从1到7报数,第三次从1到11报数.如果位于中间的三名学生从左到右依次报了3、7、11,那么 .
17.某汽车公司同时建成两条生产线,第一条生产线第一个月生产了1000辆汽车,以后每个月比前一个月多生产100辆;第二条生产线第一个月的前半个月与后半个月各生产了500辆汽车,以后每半个月比前半个月多生产50辆,那么,这两条生产线共生产20000辆汽车需 个月.
18.桌上放有多于4堆的糖块,每堆数量均不相同,而且都是不大于100的质数,其中任意三堆糖块可以平分给三位小朋友,任意四堆糖块可以平分给四位小朋友,已知其中有一堆是17块糖,则这桌子上放的糖块最多的一堆是 块.
三、解答题
19.计算
(1) (2)
20.把适当的数填写在下面的圈内并完成填空:
24和28的最大公因数是 ;
24和28的最小公倍数是 .
21.甲数除以乙数,乙数除以丙数,商相等,余数都是2.甲、乙两数之和是478,那么甲、乙、丙三数之和是多少?
22.,其中A、B均为自然数,B的最小值是多少?
23.算式的积为正数还是负数?积的末尾有多少个零?
24.在欢庆中华人民共和国成立七十周年之际,学校在一块长80米,宽24米的长方形绿地四周插上彩旗,长方形的四个角各插一面彩旗,并且要求相邻两面彩旗间的距离相等.
(1)在各个方案中,相邻两面彩旗之间最大距离是多少米?
(2)在所有方案中,至少要在绿地四周插多少面彩旗?
25.某校预初年级开展了古诗文大赛,设有一、二、三等奖.其中获得一等奖的人数占参赛人数的,获得二等奖的人数占参赛人数的,获得三等奖的人数占参赛人数的.已知该年级共有学生400人.
(1)求这次评选参赛的同学有多少名?
(2)求这次评选获得一等奖的同学有多少名?
26.一个两位数的十位上的数为a,个位上的数为b,这个两位数记作;一个三位数的百位上的数为x,十位上的数为y,个位上的数为z,这个三位数记作.
(1)(+)能被11整除吗?请说明理由;
(2)小明发现:如果能被3整除, 那么就能被3整除.请补全小明的证明思路.
27.阅读材料:的末尾数字是3,的末尾数字是9,的末尾数字是7,的末尾数字是1,的末尾数字是3,......,观察规律,,∵的末尾数字是1,∴的末尾数字是1,∴的末尾数字是3,同理可知,的末尾数字是9,的末尾数字是7.解答下列问题:
(1)的末尾数字是 ,的末尾数字是 ;
(2)求的末尾数字;
(3)求证:能被5整除.
答案
一、单选题
1.C
【分析】利用整除的定义、素数定义及合数定义判断即可
【解析】解:能够除尽的算式,商为整数,叫做被除数能被除数整除,故①错误;
最小的素数是,故②正确;
合数不一定是偶数,例如:是合数但是不是偶数,故③错误;
没有最大的素数,故④正确,
故选:C
2.B
【分析】根据能被3和5整除的数的特点,进行判断即可.
【解析】解:A.,尾数不一定是0,5,不一定能被5整除,不符合题意;
B.,尾数为0,一定能被5整除,也一定能被整除,符合题意;
C.,尾数为0,一定能被5整除,不一定能被3整除,不符合题意;
D.尾数不一定是0,5,不一定能被5整除,不符合题意;
故选B.
3.A
【分析】根据,可知,当正整数为两位数时,为或,当正整数为三位或三位以上数时,有两种情况,一种是有一个数位上的数字为4,一个数位上的数字为5,剩余数位上的数字均为1,第二种是有2个数位上的数字为2,一个数位上的数字为5,当是四位或四位以上时,剩余数位上的数字均为1,逐一进行分析即可得出结论.
【解析】解:因为,所以当正整数为两位数时,为或,或,的各个数位上数字的乘积为或;
当正整数为三位或三位以上数时:
①有一个数位上的数字为4,一个数位上的数字为5,剩余数位上的数字均为1,当尾数为1时,的尾数变为2,的各个数位上数字的乘积为:;当尾数为5时,的尾数变为6,的各个数位上数字的乘积为:;当尾数为4时,的尾数变为5,的各个数位上数字的乘积为:;
②有2个数位上的数字为2,一个数位上的数字为5,当为四位或四位以上时,剩余数位上的数字均为1,当尾数为1时,的尾数变为2,的各个数位上数字的乘积为:;当尾数为2时,的尾数变为3,的各个数位上数字的乘积为:;当尾数为5时,的尾数变为6,的各个数位上数字的乘积为:;
综上:的各个数位上数字的乘积可能为:;故均有可能,不符合题意;不可能,符合题意;
故选A.
4.D
【分析】最小的奇数为1一位数中最大的偶数为8,代入三位数中即可求解.
【解析】最小的奇数为1,所以百位数为1
一位数中最大的偶数为8,所以个位数为8
所以这个百位数是108
故答案为D.
5.B
【分析】根据整数、整除的性质分析,即可得到答案.
【解析】∵数a能被数b除尽,结果可能是整数,也可能是分数
∴数a不一定能被数b整除
∴选项B错误;
又∵其他选项均正确
故选:B.
6.C
【分析】根据,取a、b的不同值解题即可.
【解析】解:最大公因数为a、b都有的因数,
而,,
a、b不可能都含有,
不可能为a、b的最大公因数.
故选:C.
7.D
【分析】根据整除的定义可对①进行判断;分别找出24和36的素因数,得出公有的素因数可对②进行判断;根据一个整数的最大因数是它本身,一个整数的最小倍数是它本身可对③进行判断;根据整除的定义可对④进行判断;综上即可得答案.
【解析】,不能确定m、n是整数,故①错误,
24=2×2×2×3,
36=2×2×3×3,
∴24和36公有的素因数是2、2、3,故②错误,
∵一个整数的最大因数是它本身,一个整数的最小倍数是它本身,
∴整数a的最大因数正好等于整数b的最小倍数,则a=b;故③错误,
是除进不是整除,故④错误,
综上所述:错误的有①②③④,共4个,
故选:D.
8.A
【分析】要求这框苹果最少有多少个,即要求2,3,4,5的最小公倍数.
【解析】因为2,3,4和5的最小公倍数是:,
所以这筐苹果最少应有60个.
故选:A.
9.C
【分析】根据“1+2”定理:一个偶数=一个质数+一个质数×一个质数,选出符合题意的算式即可.
【解析】解析:,9是合数,所以不符合题意;
,所以不符合题意;
,三个数都是素数,符合题意;
,1不是质数,77是合数,所以不符合题意,
故选C.
10.C
【分析】根据题意所给定义新运算及素数与合数的概念直接进行求解.
【解析】解:表示不超过23的素数有2、3、5、7、11、13、17、19、23共九个,则;
表示不超过95的素数有2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89共24个,则有,
由可得;
;
故选C.
二、填空题
11. 2008 8
【分析】都是2009的因数,先找出2009的所有因数,要使得最大,那么取最大的因数2009,取最小因数1即可;求的最小值,则两个因数最接近即可.
【解析】解:因为,都是整数,大于,,
所以的最大值为,最小值为,
故答案为:2008,8.
12. 奇 2
【分析】这个数列从左到右每3个数为一组,每一组循环中前两个是奇数,第三个为偶数,,余数是2,余下的这个数是奇数;由题意知:这串数的规律是1、1、2、3、5、8…,从第三个数是前面两个数的和,分别计算这些数除以3的余数,找出规律:每8个为一循环,用2021除以8,看看有多少个循环,余数是几则看循环数里第几个数,是几就余几.
【解析】∵,
∴余数是2,所以余下的这个数是奇数;
∵一串数是:1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987…,
∴这些数除以3余数是1、1、2、0、2、2、1、0、1、1、2、0、2、2、1、0…,
∴余数中每8个为一循环,循环1、1、2、0、2、2、1、0,
∵,
∴这串数的第2021个数除以3的余数是2.
故答案为:奇,2.
13. 192,498,804 1946
【分析】设此三位数为,可得一定能被17整除,据此求出b的值即可;
设此四位数为,可得一定能被131整除,据此求出y的值即可.
【解析】设此三位数为, 可得到,所以一定能被17整除,,27,44.
这个三位数为192,498,804.
设此四位数为,可得到,所以一定能被131整除,,145(太大),
这个四位数是1946.
故答案为:192,498,804;1946
14.60,24,15或120,12,15
【分析】根据题意得甲是60或120,然后将120分解质因数,分情况讨论即可.
【解析】解:根据题意得:甲的因数有12也有15,那么甲最小是12与15的最小公倍数,即甲最小是60,又因为三个数最小公倍数是120,所以甲一定是120的因数,
∴甲是60或120,
把他们的最小公倍数120分解质因数,
,
当甲是60时 ,
所以丙为,
乙为 ,
当甲为120时,乙为 ,
丙为,
∴甲乙丙分别为 60,24,15或120,12,15.
15.16
【分析】根据能够被2整除的数的个位为偶数,先确定个位数,再根据能够被3整除的数的特征确定A,B即可.
【解析】解:能被2整除,则为0、2、4、6、8;
能被3整除,则能
被3整除.当时,A可为1、4、7;
当时,A可为2、5、8;
当时,A可为0、3、6、9;
当时,A可为1、4、7;
当时,A可为2、5、8;
所以这样的五位数有16个.
故答案为:16
16.
【分析】设位于中间的三名学生是第n名,名,名,由题意可知n能被3整除,能被7整除,能被11整除,先找出最小的两个连续自然数分别能被7和11整除,确定出前面的连续自然数,再加上7和11的最小公倍数使得结果能被3整除即可得到这三个连续自然数中最小的自然数,然后可得答案.
【解析】解:设位于中间的三名学生是第n名,名,名,则,
由题意得:n能被3整除,能被7整除,能被11整除,
分别能被7和11整除的两个连续自然数为21和22,前面的连续自然数是20,
7和11的最小公倍数是77,考虑20加上77的整数倍,使得结果能被3整除,
当时,97不能被3整数,不符合题意;
当时,174能被3整数,符合题意,
所以位于中间的三名学生是第174名,175名,176名,
所以,
故答案为:.
17.7.
18.89
【分析】各堆糖块数被3除都余2,被4除余1,则每堆糖块的数量都是块且是不大于100的质数,这些质数只有5,17,29,41,53,89,据此即可求解.
【解析】解:因为任意3堆数量之和能被3整除,所以每堆被3除的余数相同,又因为17被3除余2,所以各堆糖块数被3除都余2;同理,各堆糖块数被4除余1,所以每堆糖块的数量都是块,且是小于100的质数,这些质数只有5,17,29,41,53,89,
即这桌子上放的糖块最多的一堆是89,
故答案为:89.
三、解答题
19.(1)
(2)
20.解:如图所示:
∵24=2×2×2×3,
∴24 和 28 的最大公因数:4;
24 和 28 的最小公倍数:168.
21.解:由“余数是2,甲、乙两数之和是478”,因此是乙的倍数,因为,
甲数除以乙数,乙数除以丙数,商相等,余数都是2,则剔除商比乙大或商小于3的组合.
容易得到:(,,),
则甲、乙、丙三数之和:;
同理:(,,),
甲、乙、丙三数之和为:;
(,,),
甲、乙、丙三数之和为:.
答:甲、乙、丙三数之和是或或.
22.解:因为,
所以,
所以,
所以.
23.解:由题意知,算式中有15个负数,所以根据有理数的乘法法则,积为负数;
又5与任何一个偶数相乘的得数末尾必为0,且在1-30的30个数里面末尾为5的数有5,15,25,
∴5,15与偶数乘,各得1个0,25与4乘可得2个0,又10、20、30各有1个0,
所以,积的末尾共有7个0.
24.(1)解:∵,,
∴80与24的最大公因数是8,
∵相邻两面彩旗间的距离相等,
∴即相邻两面彩旗间最大距离是8米;
(2)解:要使得使用的彩旗数量最少,则要求相邻两面彩旗之间的距离最大,
根据(1)结果可知相邻两面彩旗间最大距离是8米,
即:,,
∴长方形的长边植树11棵,宽边植树4棵,
∴则总的彩旗数量为:(面).
答:至少在绿地四周插26面彩旗.
25.(1)∵,
∴、、的最小公倍数是,
答:这次评选参赛的同学有名;
(2)由(1)可知这次评选参赛的同学有名,
∴评选获得一等奖的同学有名,
答:这次评选获得一等奖的同学有名.
26.(1)解:能被整除,理由为:
,
∴能被整除.
(2)解:
,
∵,都能被3整除,
∴就能被3整除,
故答案为:,.
27.(1)解:,
的末尾数字为3;
的末尾数字是4,的末尾数字是6,的末尾数字是4,…
的末尾数字是4,的末尾数字是6,
的末尾数字是6;
故答案为:3,6;
(2)解:,
∵的末尾数字是6,
∴的末尾数字是4;
(3)证明:∵的末尾数字是2,的末尾数字是4,的末尾数字是8,的末尾数字是6,的末尾数字是2,…
的末尾数字是2,的末尾数字是4,的末尾数字是8,的末尾数字是6,
的末尾数字为6;
同理可得:
的末尾数字7,的末尾数字9,的末尾数字3,的末尾数字1;
的末尾数字9,
∴的末尾数字是5,
∴能被5整除.
