专题九旋转模型 课件 (共30张PPT)2024年中考数学专题突破
文档属性
| 名称 | 专题九旋转模型 课件 (共30张PPT)2024年中考数学专题突破 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 19:17:40 | ||
图片预览








文档简介
(共30张PPT)
专题九
旋转模型
思维指导
SI WEI ZHI DAO
PART ONE
01
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
旋转常常出现在等腰三角形、等边三角形、正方形中,是重点也是难点.我们要抓住旋转的本质——全等. 压轴题中需要学生做旋转变换,难度较大.
题型突破
TI XING TU PO
PART TWO
02
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
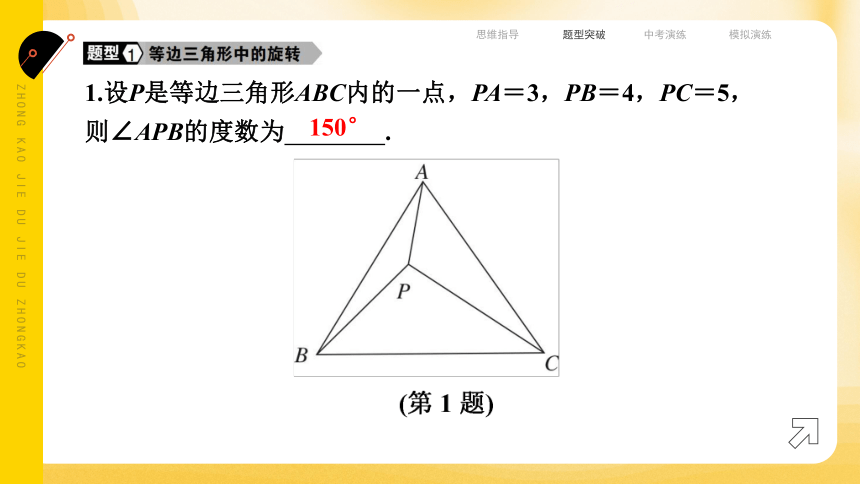
1.设P是等边三角形ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数为 .
150°
解析:∵△ABC为等边三角形,∴BA=BC,∠ABC=60°.
将△BPC绕点B逆时针旋转60°得到△BEA,连接EP.
∴BE=BP=4,AE=PC=5,∠PBE=60°.
∴△BPE为等边三角形.
∴PE=PB=4,∠BPE=60°.
在△AEP中,AE=5,AP=3,PE=4,∴AE2=PE2+PA2.
∴△APE为直角三角形,且∠APE=90°.
∴∠APB=∠APE+∠BPE=90°+60°=150°.
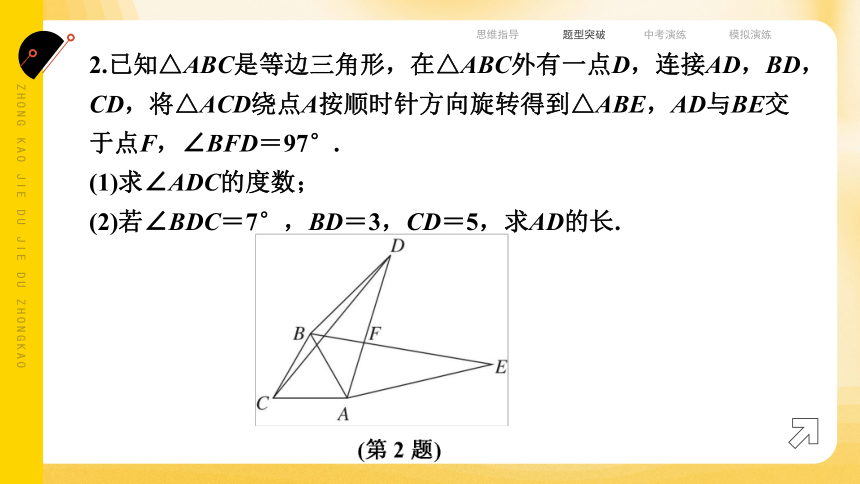
2.已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°.
(1)求∠ADC的度数;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠DAE=∠CAB=60°.
∵∠BFD=97°=∠AFE,∴∠E=180°-97°-60°=23°.
∴∠ADC=∠E=23°.
(2)连接DE.
∵AD=AE,∠DAE=60°,∴△AED是等边三角形.
∴∠ADE=60°,AD=DE.
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE.∴CD=BE=5.
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,DE=.
∴DE=4.∴AD=DE=4.
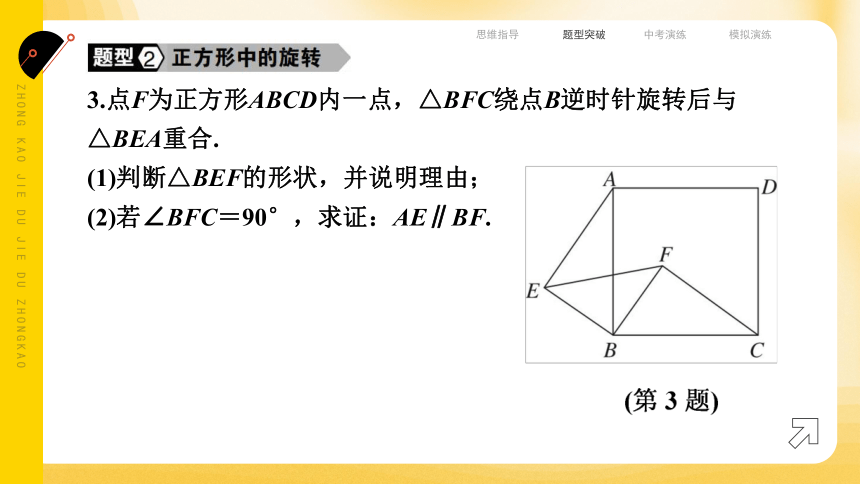
3.点F为正方形ABCD内一点,△BFC绕点B逆时针旋转后与△BEA重合.
(1)判断△BEF的形状,并说明理由;
(2)若∠BFC=90°,求证:AE∥BF.
(1)解:△BEF是等腰直角三角形.理由如下:
∵四边形ABCD是正方形,∴∠ABC=90°.
∵△BFC绕点B逆时针旋转后与△BEA重合,
∴∠EBF=∠ABC=90°,BE=BF.
∴△BEF是等腰直角三角形.
(2)证明:∵△BFC绕点B逆时针旋转后与△BEA重合,
∴∠AEB=∠BFC=90°.
又∵∠EBF=90°,∴∠AEB+∠EBF=90°+90°=180°.
∴AE∥BF.
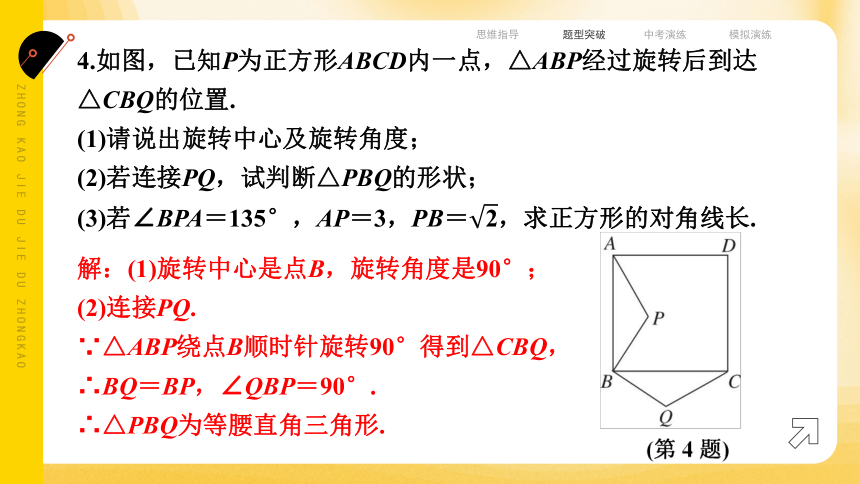
4.如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
(1)请说出旋转中心及旋转角度;
(2)若连接PQ,试判断△PBQ的形状;
(3)若∠BPA=135°,AP=3,PB=,求正方形的对角线长.
解:(1)旋转中心是点B,旋转角度是90°;
(2)连接PQ.
∵△ABP绕点B顺时针旋转90°得到△CBQ,
∴BQ=BP,∠QBP=90°.
∴△PBQ为等腰直角三角形.
(3)连接AC.
∵△ABP绕点B顺时针旋转90°得到△CBQ,
∴∠BQC=∠BPA=135°,CQ=AP=3.
∵△PBQ为等腰直角三角形,∴∠BPQ=∠BQP=45°.
又∵∠BPA=135°,
∴∠BPA+∠BPQ=135°+45°=180°.
∴点A,P,Q三点在同一条直线上.
∵PQ==2,
∴AQ=AP+PQ=3+2=5.
∵∠AQC=∠BQC-∠BQP=135°-45°=90°,
∴在Rt△AQC中,AC=.
5.如图,在等腰直角三角形MNC中,∠CNM=90°且CN=MN,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,
(1)判断△CAM的形状并证明;
(2)若AB=3,求AM的长.
解:(1)△CAM是等边三角形.理由如下:
∵将△MNC绕点C顺时针旋转60°得到△ABC,
∴CM=AC,∠ACM=60°.
∴△ACM是等边三角形.
(2)∵将△MNC绕点C顺时针旋转60°得到△ABC,
∴AB=MN=3,∠ABC=∠CNM=90°.
∴AC=AB=6.
又∵△ACM是等边三角形,∴AM=AC=6.
6.两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25. 保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)在图2中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一条直线上(如图3)时,若AC=7,求CD的长.
(1)证明:延长BD交OA于点G,交AC于点E.
∵∠AOB=∠COD=90°,∴∠AOC=∠BOD.
在△AOC和△BOD中, OA=OB, ∠AOC=∠BOD, OC=OD,
∴△AOC≌△BOD(SAS).
∴AC=BD,∠CAO=∠DBO.
又∵∠DBO+∠OGB=90°,∠OGB=∠AGE,
∴∠CAO+∠AGE=90°.
∴∠AEG=90°,即BD⊥AC.
(2)解:∵∠OCD=∠ODC=45°,
BD与CD在同一条直线上,
∴∠ODB=180°-∠ODC=180°-45°=135°.
∵△AOC≌△BOD,
∴∠ACO=∠ODB=135°,AC=BD=7,
由(1)知∠ACB=90°.
∴BC==24.
∴CD=BC-BD=24-7=17.
中考演练
ZHONG KAO YAN LIAN
PART THREE
03
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
【例】(2023·白云二模)
(1)【问题发现】如图1,△ABC和△ADE均为正三角形,B,D,E三点共线. 猜想线段BD,CE之间的数量关系为 ;∠BEC= °.
60
BD=CE
(2)【类比探究】如图2,△ABC和△ADE均为等腰直角三角形,∠ACB=∠AED=90°,AC=BC,AE=DE,B,D,E三点共线,线段BE,AC交于点F.此时,线段BD,CE之间的数量关系是什么?请写出证明过程并求出∠BEC的度数.
(2)解:结论:BD=CE,∠BEC=45°.理由如下:
∵△ABC和△ADE均为等腰直角三角形,
∴∠BAC=∠ABC=∠ADE=∠DAE=45°,∠ACB=∠AED=90°.
∴∠BAD=∠CAE,∠ADB=135°.在Rt△ABC中,sin∠ABC=
∴. 又∵∠BAD=∠CAE,∴△ABD∽△ACE.
∴∠ADB=∠AEC=135°,∴
,∴ ∴
∴CE.
(3)【拓展延伸】如图3,在△ABC中,∠BAC=90°,∠B=30°,BC=8,DE为△ABC的中位线,将△ADE绕点A顺时针方向旋转,当DE所在直线经过点B时,请直接写出CE的长.
(3)∵∠BAC=90°,∠ABC=30°,BC=8,∴AC=
∴.
∵DE为△ABC的中位线,∴DE=
AB.
∴∠ADE=∠ABC=30°,.
图4
根据题意,将△ADE绕点A顺时针方向旋转,当DE所在直线经过点B时,
分两种情况讨论:
①如图4所示.
由旋转的性质,得∠BAD=∠CAE.
∵ ,∴△BAD∽△CAE.
∴ ,∠ADB=∠AEC=180°-∠ADE=150°.
∵∠AED=90°-∠ADE=60°,
∴∠CEB=∠AEC-∠AED=150°-60°=90°.
设CE=x,则BD=x+4.
在Rt△BCE中,由勾股定理,得x2+(
(舍去).
∴CE=.
②如图5所示.由旋转的性质,得∠BAD=∠CAE.
∵ ,∴ △AEC∽△ADB.
∴
y-4.
在Rt△BCE中,由勾股定理,得y2+(
(舍去).
∴CE=
.
图5
模拟演练
MO NI YAN LIAN
PART FOUR
04
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
1.(2023·执信中学二模节选)如图1,点D是边长为4的等边三角形ABC内部一点,满足BD=DC,且∠BDC=120°,点E为BD延长线与边AC的交点.
(1)求DE的长;
(2)若△BDC绕点C顺时针旋转至△B'D'C处,如图2,点B的对应点为点B',点D对应点为点D',连接AB'并取AB'的中点G,连接BG,D'G.试探究BG与D'G的关系,并说明理由.
(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.
∵DB=DC,∠BDC=120°,∴∠DBC=∠DCB=30°.
∴∠ABD=∠ACD=30°.
∴∠EBC+∠ECB=90°.∴∠BEC=90°.
∴DE=
∵∴
∴.
(2)解:BG⊥GD',BG=GD'.理由如下:
如图2,延长BG到点T,使得GT=GB,连接B'T,TD',延长BA交D'B'于点K.
∵AG=B'G,∠AGB=∠B'GT,BG=TG,∴△AGB≌△B'GT(SAS).
∴AB=TB',∠ABG=∠GTB'.
∴BK∥TB'.∴∠K=∠KB'T.
∵∠ABC=60°,BC=AB,∠CD'B'=120°,
∴BC=TB',∠KBC+∠CD'K=180°.
∴∠K+∠BCD'=180°.
∵∠KB'T+∠TB'D'=180°,∴∠BCD'=∠TB'D'.
∵CD'=B'D',∴△BCD'≌△TB'D'(SAS).
∴D'B=D'T,∠CD'B=∠TD'B'.
∴∠BD'T=∠CD'B'=120°.
∵GB=GT,∴D'G⊥BT,∠BD'G=∠TD'G=60°.
∴∠BGD'=90°,∠D'BG=30°.∴BG=GD'.
∴BG⊥GD',BG=GD'.
图2
专题九
旋转模型
思维指导
SI WEI ZHI DAO
PART ONE
01
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
旋转常常出现在等腰三角形、等边三角形、正方形中,是重点也是难点.我们要抓住旋转的本质——全等. 压轴题中需要学生做旋转变换,难度较大.
题型突破
TI XING TU PO
PART TWO
02
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
1.设P是等边三角形ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数为 .
150°
解析:∵△ABC为等边三角形,∴BA=BC,∠ABC=60°.
将△BPC绕点B逆时针旋转60°得到△BEA,连接EP.
∴BE=BP=4,AE=PC=5,∠PBE=60°.
∴△BPE为等边三角形.
∴PE=PB=4,∠BPE=60°.
在△AEP中,AE=5,AP=3,PE=4,∴AE2=PE2+PA2.
∴△APE为直角三角形,且∠APE=90°.
∴∠APB=∠APE+∠BPE=90°+60°=150°.
2.已知△ABC是等边三角形,在△ABC外有一点D,连接AD,BD,CD,将△ACD绕点A按顺时针方向旋转得到△ABE,AD与BE交于点F,∠BFD=97°.
(1)求∠ADC的度数;
(2)若∠BDC=7°,BD=3,CD=5,求AD的长.
解:(1)∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴AB=AC,∠ADC=∠E,∠DAE=∠CAB=60°.
∵∠BFD=97°=∠AFE,∴∠E=180°-97°-60°=23°.
∴∠ADC=∠E=23°.
(2)连接DE.
∵AD=AE,∠DAE=60°,∴△AED是等边三角形.
∴∠ADE=60°,AD=DE.
∵将△ACD绕点A按顺时针方向旋转得到△ABE,
∴△ACD≌△ABE.∴CD=BE=5.
∵∠BDC=7°,∠ADC=23°,∠ADE=60°,
∴∠BDE=90°,DE=.
∴DE=4.∴AD=DE=4.
3.点F为正方形ABCD内一点,△BFC绕点B逆时针旋转后与△BEA重合.
(1)判断△BEF的形状,并说明理由;
(2)若∠BFC=90°,求证:AE∥BF.
(1)解:△BEF是等腰直角三角形.理由如下:
∵四边形ABCD是正方形,∴∠ABC=90°.
∵△BFC绕点B逆时针旋转后与△BEA重合,
∴∠EBF=∠ABC=90°,BE=BF.
∴△BEF是等腰直角三角形.
(2)证明:∵△BFC绕点B逆时针旋转后与△BEA重合,
∴∠AEB=∠BFC=90°.
又∵∠EBF=90°,∴∠AEB+∠EBF=90°+90°=180°.
∴AE∥BF.
4.如图,已知P为正方形ABCD内一点,△ABP经过旋转后到达△CBQ的位置.
(1)请说出旋转中心及旋转角度;
(2)若连接PQ,试判断△PBQ的形状;
(3)若∠BPA=135°,AP=3,PB=,求正方形的对角线长.
解:(1)旋转中心是点B,旋转角度是90°;
(2)连接PQ.
∵△ABP绕点B顺时针旋转90°得到△CBQ,
∴BQ=BP,∠QBP=90°.
∴△PBQ为等腰直角三角形.
(3)连接AC.
∵△ABP绕点B顺时针旋转90°得到△CBQ,
∴∠BQC=∠BPA=135°,CQ=AP=3.
∵△PBQ为等腰直角三角形,∴∠BPQ=∠BQP=45°.
又∵∠BPA=135°,
∴∠BPA+∠BPQ=135°+45°=180°.
∴点A,P,Q三点在同一条直线上.
∵PQ==2,
∴AQ=AP+PQ=3+2=5.
∵∠AQC=∠BQC-∠BQP=135°-45°=90°,
∴在Rt△AQC中,AC=.
5.如图,在等腰直角三角形MNC中,∠CNM=90°且CN=MN,将△MNC绕点C顺时针旋转60°,得到△ABC,连接AM,
(1)判断△CAM的形状并证明;
(2)若AB=3,求AM的长.
解:(1)△CAM是等边三角形.理由如下:
∵将△MNC绕点C顺时针旋转60°得到△ABC,
∴CM=AC,∠ACM=60°.
∴△ACM是等边三角形.
(2)∵将△MNC绕点C顺时针旋转60°得到△ABC,
∴AB=MN=3,∠ABC=∠CNM=90°.
∴AC=AB=6.
又∵△ACM是等边三角形,∴AM=AC=6.
6.两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25. 保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)在图2中,求证:AC=BD,且AC⊥BD;
(2)当BD与CD在同一条直线上(如图3)时,若AC=7,求CD的长.
(1)证明:延长BD交OA于点G,交AC于点E.
∵∠AOB=∠COD=90°,∴∠AOC=∠BOD.
在△AOC和△BOD中, OA=OB, ∠AOC=∠BOD, OC=OD,
∴△AOC≌△BOD(SAS).
∴AC=BD,∠CAO=∠DBO.
又∵∠DBO+∠OGB=90°,∠OGB=∠AGE,
∴∠CAO+∠AGE=90°.
∴∠AEG=90°,即BD⊥AC.
(2)解:∵∠OCD=∠ODC=45°,
BD与CD在同一条直线上,
∴∠ODB=180°-∠ODC=180°-45°=135°.
∵△AOC≌△BOD,
∴∠ACO=∠ODB=135°,AC=BD=7,
由(1)知∠ACB=90°.
∴BC==24.
∴CD=BC-BD=24-7=17.
中考演练
ZHONG KAO YAN LIAN
PART THREE
03
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
【例】(2023·白云二模)
(1)【问题发现】如图1,△ABC和△ADE均为正三角形,B,D,E三点共线. 猜想线段BD,CE之间的数量关系为 ;∠BEC= °.
60
BD=CE
(2)【类比探究】如图2,△ABC和△ADE均为等腰直角三角形,∠ACB=∠AED=90°,AC=BC,AE=DE,B,D,E三点共线,线段BE,AC交于点F.此时,线段BD,CE之间的数量关系是什么?请写出证明过程并求出∠BEC的度数.
(2)解:结论:BD=CE,∠BEC=45°.理由如下:
∵△ABC和△ADE均为等腰直角三角形,
∴∠BAC=∠ABC=∠ADE=∠DAE=45°,∠ACB=∠AED=90°.
∴∠BAD=∠CAE,∠ADB=135°.在Rt△ABC中,sin∠ABC=
∴. 又∵∠BAD=∠CAE,∴△ABD∽△ACE.
∴∠ADB=∠AEC=135°,∴
,∴ ∴
∴CE.
(3)【拓展延伸】如图3,在△ABC中,∠BAC=90°,∠B=30°,BC=8,DE为△ABC的中位线,将△ADE绕点A顺时针方向旋转,当DE所在直线经过点B时,请直接写出CE的长.
(3)∵∠BAC=90°,∠ABC=30°,BC=8,∴AC=
∴.
∵DE为△ABC的中位线,∴DE=
AB.
∴∠ADE=∠ABC=30°,.
图4
根据题意,将△ADE绕点A顺时针方向旋转,当DE所在直线经过点B时,
分两种情况讨论:
①如图4所示.
由旋转的性质,得∠BAD=∠CAE.
∵ ,∴△BAD∽△CAE.
∴ ,∠ADB=∠AEC=180°-∠ADE=150°.
∵∠AED=90°-∠ADE=60°,
∴∠CEB=∠AEC-∠AED=150°-60°=90°.
设CE=x,则BD=x+4.
在Rt△BCE中,由勾股定理,得x2+(
(舍去).
∴CE=.
②如图5所示.由旋转的性质,得∠BAD=∠CAE.
∵ ,∴ △AEC∽△ADB.
∴
y-4.
在Rt△BCE中,由勾股定理,得y2+(
(舍去).
∴CE=
.
图5
模拟演练
MO NI YAN LIAN
PART FOUR
04
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
1.(2023·执信中学二模节选)如图1,点D是边长为4的等边三角形ABC内部一点,满足BD=DC,且∠BDC=120°,点E为BD延长线与边AC的交点.
(1)求DE的长;
(2)若△BDC绕点C顺时针旋转至△B'D'C处,如图2,点B的对应点为点B',点D对应点为点D',连接AB'并取AB'的中点G,连接BG,D'G.试探究BG与D'G的关系,并说明理由.
(1)证明:∵△ABC是等边三角形,∴∠ABC=∠ACB=60°.
∵DB=DC,∠BDC=120°,∴∠DBC=∠DCB=30°.
∴∠ABD=∠ACD=30°.
∴∠EBC+∠ECB=90°.∴∠BEC=90°.
∴DE=
∵∴
∴.
(2)解:BG⊥GD',BG=GD'.理由如下:
如图2,延长BG到点T,使得GT=GB,连接B'T,TD',延长BA交D'B'于点K.
∵AG=B'G,∠AGB=∠B'GT,BG=TG,∴△AGB≌△B'GT(SAS).
∴AB=TB',∠ABG=∠GTB'.
∴BK∥TB'.∴∠K=∠KB'T.
∵∠ABC=60°,BC=AB,∠CD'B'=120°,
∴BC=TB',∠KBC+∠CD'K=180°.
∴∠K+∠BCD'=180°.
∵∠KB'T+∠TB'D'=180°,∴∠BCD'=∠TB'D'.
∵CD'=B'D',∴△BCD'≌△TB'D'(SAS).
∴D'B=D'T,∠CD'B=∠TD'B'.
∴∠BD'T=∠CD'B'=120°.
∵GB=GT,∴D'G⊥BT,∠BD'G=∠TD'G=60°.
∴∠BGD'=90°,∠D'BG=30°.∴BG=GD'.
∴BG⊥GD',BG=GD'.
图2
同课章节目录
