专题十 几何综合 课件(共35张PPT) 2024年中考数学专题突破
文档属性
| 名称 | 专题十 几何综合 课件(共35张PPT) 2024年中考数学专题突破 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
专题十
几何综合
思维指导
SI WEI ZHI DAO
PART ONE
01
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
几何综合题型一般以基本图形(正方形、特殊平行四边形、等边、等腰、直角三角形等)为载体,考查运用图形变换分析图形中基本量之间的数量关系的探究过程.解决这类问题的思路是从复杂的图形中“抽”出简单图形,在简单图形中进行逻辑推导,应用相关几何模型,找到解题思路.
题型突破
TI XING TU PO
PART TWO
02
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
1.(2022·越秀一模)如图,在直角梯形ABCD中,∠D=∠C=90°,AB=4,BC=6,AD=8.点P,Q同时从点A出发,分别做匀速运动.其中点P沿AB,BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一个点到达自己的终点时,另一个点也停止运动,设这两点从出发运动了t s.
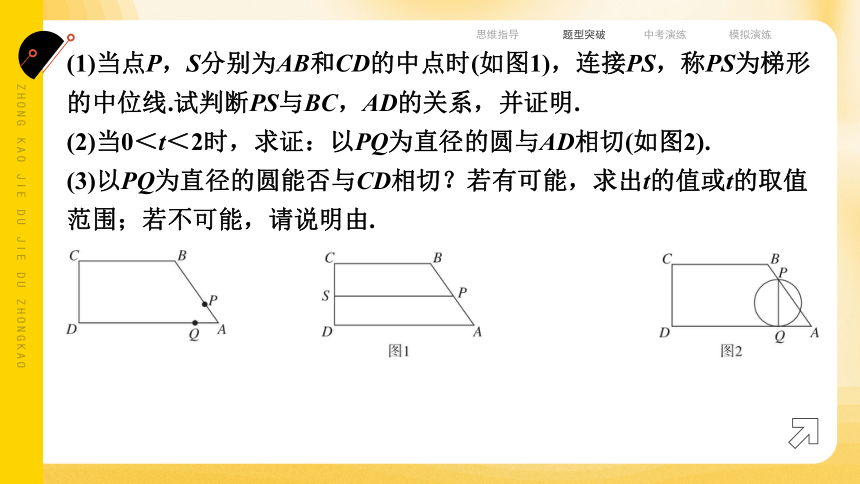
(1)当点P,S分别为AB和CD的中点时(如图1),连接PS,称PS为梯形的中位线.试判断PS与BC,AD的关系,并证明.
(2)当0<t<2时,求证:以PQ为直径的圆与AD相切(如图2).
(3)以PQ为直径的圆能否与CD相切?若有可能,求出t的值或t的取值范围;若不可能,请说明由.
(1)解:结论:PS∥AD∥BC,PS=(AD+BC).
理由:连接CP并延长,交DA的延长线于点E,∵CB∥DE,
∴∠B=∠PAE.∵PS是梯形的中位线,∴CS=SD,BP=PA.
在△CBP和△EAP中,
∴△CBP ≌△EAP(ASA).∴CP=PE,BC=AE.
∴SP∥DE,SP=(AD+BC).
∴PS∥AD∥BC,PS=(AD+BC).
(2)证明:当0<t<2时,过点B作BE⊥AD,垂足为E.
∵在直角梯形ABCD中,∠D=∠C=90°,
AB=4,BC=6,AD=8.∴AE=AD-BC=8-6=2.
∴.
∵∠A=∠A,∴△APQ ∽△ABE.∴∠PQA=∠BEA=90°.
∵PQ为直径,∴以PQ为直径的圆与AD相切.
(3)当0<t<2时,以PQ为直径的圆与CD不可能相切.当2≤t≤5时,
t=时,以PQ为直径的圆与CD相切.
设以PQ为直径的☉O与CD相切于点K,如图.
则有PC=10-2t,DQ=8-t,OK⊥DC.
∵OK是梯形PCDQ的中位线,∴PQ=2OK=PC+DQ=18-3t.
在直角梯形PCDQ中,PQ2=CD2+(DQ-CP)2,解得t=.
∵<5,
因此,当t=时,以PQ为直径的圆与CD相切.
2.四边形ABCD是边长为2的正方形,E是AB的中点,连接DE,F是射线BC上一动点(不与点B重合),连接AF,交DE于点G.
(1)如图1,当F是BC的中点时,求证:△ABF≌△DAE.
(2)如图2,当点F与点C重合时,求AG的长.
(3)在点F运动的过程中,当线段BF为何值时,AG=AE?请说明理由.
(1)证明:∵四边形ABCD是正方形,∴∠B=∠DAE=90°,
AB=AD=BC.
∵E,F分别是AB,BC的中点,∴AE=BC.∴AE=BF.
在△ABF和△PAE中,
∴△ABF≌△DAE(SAS).
(2)解:∵在正方形ABCD中,AB∥CD,∠ADC=90°,
AD=CD=2,
∴AC=.∵AB∥CD,
∴△AGE∽△CGD.
∴.
(3)解:当BF=时,AG=AE.理由如下:如图,设AF交CD于点M.
若使AG=AE=1,则有∠1=∠2,∵AB∥CD,∴∠1=∠4.
又∵∠2=∠3,∴∠3=∠4.∴DM=MG.
在Rt△ADM中,AM2-DM2=AD2,即(DM+1)2-DM2=22,
解得DM=∴.
∵AB∥CD,∴△ABF∽△MCF.
∴.
解得BF=∴时,AG=AE.
3.如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4. E是AD的中点,以DE为边作正方形DEFG,连接AG,CE. 将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).
(1)如图2,在旋转过程中,
①判断△AGD与△CED是否全等,并说明理由.
②当CE=CD时,AG与EF交于点H,求GH的长.
(2)如图3,延长CE交直线AG于点P.
①求证:AG⊥CP.
②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(1)解:①△AGD≌△CED. 理由如下:∵四边形EFGD是正方形,
∴DG=DE,∠GDE=90°.
∵DA=DC,∠ADC=90°,∴∠GDE=∠ADC.
∴∠GDE-∠ADE=∠ADC-∠ADE,即∠ADG=∠CDE.
在△AGD和△CED中,
∴△AGD≌△CED(SAS).
②如图1,过点A作AT⊥GD于点T.∵△AGD≌△CED,CD=CE,
∴AD=AG=4.∵AT⊥GD,∴TG=TD=1.
∴AT=.
∵EF∥DG,∴∠GHF=∠AGT.∵∠F=∠ATG=90°,∴△GFH∽△ATG.
∴ ∴
∴.
(2)①证明:如图2,设AD交PC于点O.
∵△AGD≌△CED,∴∠DAG=∠DCE.
∵∠DCE+∠COD=90°,∠COD=∠AOP,
∴∠AOP+∠DAG=90°.
∴∠APO=90°.∴CP⊥AG.
②解:∵∠CPA=90°,AC是定值,
∴当∠ACP最小时,PC的值最大.
∴当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与点P重合(如图3所示).
∵∠CED=90°,CD=4,DE=2,
∴EC=.
∵EF=DE=2,∴CP=CE+EF=2+2.
∴PC的最大值为2+2.
中考演练
ZHONG KAO YAN LIAN
PART THREE
03
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
【例】(2022·南沙一模)如图1,在正方形ABCD中,E为AD边上的一点,连接CE,过点D作DF⊥CE于点G,DF交AB于点F.已知DG=4,CG=16.
(1)EG的长是 1 ;
(2)如图2,以点G为圆心,GD为半径的圆与线段DF,CE分别交于M,N两点.
①连接CM,BM,若P为BM的中点,连接CP,
求证:∠BCP=∠MCP;
②连接BN,若Q为BN的中点,连接CQ,求线段CQ的长.
(2)①证明:连接CM,BM,CP.
∵G为DM的中点,CG⊥DM,∴CM=CD.
∵CD=CB,∴CB=CM.
∵P为BM的中点,∴∠BCP=∠MCP.
②解:过点Q作QH⊥CD于点H,
连接NH并延长交BC的延长线于点L,
过点N作NK⊥CD于点K.
在Rt△CGD中,DG=4,CG=16,
则CD=.
∵CG=16,GN=4,∴CN=16-4=12.
∵∠CGD=∠CKN=90°,∠NCK=∠DCG,
∴△CKN ∽△CGD.
∴.
解得CK=.
∵QH⊥CD,∠DCB=90°,
NK⊥CD,
∴NK∥QH∥BC.
∵NQ=QB,
∴KH=HC=.
易证QH=.
∴CQ=.
模拟演练
MO NI YAN LIAN
PART FOUR
04
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
1.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接BE,M,N,P分别为DE,BE,BC的中点.
(1)【观察猜想】
图1中,线段NM,NP的数量关系是 ,∠MNP的度数为 ;
60°
NM=NP
(2)【探究证明】
把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP,BD,CE,判断△MNP的形状,并说明理由;
(3)【拓展延伸】
把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请求出△MNP面积的最大值.
(2)解:△MNP是等边三角形.理由如下:
由旋转可得,∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴BD=CE,∠ABD=∠ACE.
∵M,N,P分别为DE,BE,BC的中点.
∴MN=CE,MN∥BD,PN∥CE.
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE.
∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB.
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE=∠ENM,
∴∠MNP=∠ENP+∠ENM=(∠EBC+∠ACE)+(∠ABE+∠ECB)=180°-∠BAC=60°.
∴△MNP是等边三角形.
(3)根据题意,得BD≤AB+AD,即BD≤4.∴MN≤2.
∴△MNP的面积=MN2.
∴△MNP的面积的最大值为.
2.如图1,四边形ABCD的对角线AC,BD相交于点O,OA=OC,
OB=OD+CD.
(1)过点A作AE∥DC交BD于点E,
①求证:△AOE≌△COD;
②求证:AE=BE;
(2)如图2,将△ABD沿AB翻折得到△ABD',若AD'∥BC,
求证:CD2=2OD·BD.
证明:(1)①∵AE∥DC,
∴∠CDO=∠AEO,∠DCO=∠EAO.
在△AOE和△COD中,
∴△AOE≌△COD(AAS).
②∵△AOE≌△COD,∴CD=AE,OD=OE.
∵OB=OE+BE,OB=OD+CD,
∴BE=CD. ∴AE=BE.
(2)过点A作AF∥DC交BD于点E,交BC于点F.
∵AD'∥BC,∴∠D'AB=∠ABC.
由翻折可知,∠D'AB=∠DAB,∴∠ABC=∠DAB.
∵AE=BE,∴∠ABD=∠EAB.
∴∠ABC-∠ABD=∠DAB-∠EAB,
即∠DBC=∠DAE.
∵AE∥DC,∴∠AED=∠CDB. ∴△ADE∽△BCD.
∴.∴AE·CD=DE·BD.
由②可知,AE=CD,OD=EO.
∴DE=2OD.∴CD2=2OD·BD.
3.(2022·南沙一模)如图,在△ABC中,∠ABC=90°,过点B作BD⊥AC于点D.
(1)尺规作图:作边BC的垂直平分线,交边AC于点E;
(2)若AD∶BD=3∶4,求sin C的值;
(3)已知BC=10,BD=6.若点P为平面内任意一动点,且保持∠BPC=90°,求线段AP的最大值.
解:(1)如图1即为所求,
(2)设AD=3x,BD=4x.
∴AB==5x.
∵∠ABC=90°,∴∠ABD+∠DBC=90°.
∵BD⊥AC,∴∠DBC+∠C=90°.
∴∠C=∠ABD.
∴sin C=sin∠ABD=.
(3)如图2,以BC为直径作圆O,连接AO交圆于两点P1,P2,
当P与P2重合时,AP取最大值AP2.连接BP1,BP2.
∵sin∠ABD=,
∴sin∠BAD=
∴.
在Rt△ABO中,AO2=AB2+OB2.
∴AO=.
∴线段AP的最大值是AP2=+5.
专题十
几何综合
思维指导
SI WEI ZHI DAO
PART ONE
01
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
几何综合题型一般以基本图形(正方形、特殊平行四边形、等边、等腰、直角三角形等)为载体,考查运用图形变换分析图形中基本量之间的数量关系的探究过程.解决这类问题的思路是从复杂的图形中“抽”出简单图形,在简单图形中进行逻辑推导,应用相关几何模型,找到解题思路.
题型突破
TI XING TU PO
PART TWO
02
SPORT
中考解读 解读中考
2024
题型突破
中考演练
思维指导
模拟演练
1.(2022·越秀一模)如图,在直角梯形ABCD中,∠D=∠C=90°,AB=4,BC=6,AD=8.点P,Q同时从点A出发,分别做匀速运动.其中点P沿AB,BC向终点C运动,速度为每秒2个单位,点Q沿AD向终点D运动,速度为每秒1个单位.当这两点中有一个点到达自己的终点时,另一个点也停止运动,设这两点从出发运动了t s.
(1)当点P,S分别为AB和CD的中点时(如图1),连接PS,称PS为梯形的中位线.试判断PS与BC,AD的关系,并证明.
(2)当0<t<2时,求证:以PQ为直径的圆与AD相切(如图2).
(3)以PQ为直径的圆能否与CD相切?若有可能,求出t的值或t的取值范围;若不可能,请说明由.
(1)解:结论:PS∥AD∥BC,PS=(AD+BC).
理由:连接CP并延长,交DA的延长线于点E,∵CB∥DE,
∴∠B=∠PAE.∵PS是梯形的中位线,∴CS=SD,BP=PA.
在△CBP和△EAP中,
∴△CBP ≌△EAP(ASA).∴CP=PE,BC=AE.
∴SP∥DE,SP=(AD+BC).
∴PS∥AD∥BC,PS=(AD+BC).
(2)证明:当0<t<2时,过点B作BE⊥AD,垂足为E.
∵在直角梯形ABCD中,∠D=∠C=90°,
AB=4,BC=6,AD=8.∴AE=AD-BC=8-6=2.
∴.
∵∠A=∠A,∴△APQ ∽△ABE.∴∠PQA=∠BEA=90°.
∵PQ为直径,∴以PQ为直径的圆与AD相切.
(3)当0<t<2时,以PQ为直径的圆与CD不可能相切.当2≤t≤5时,
t=时,以PQ为直径的圆与CD相切.
设以PQ为直径的☉O与CD相切于点K,如图.
则有PC=10-2t,DQ=8-t,OK⊥DC.
∵OK是梯形PCDQ的中位线,∴PQ=2OK=PC+DQ=18-3t.
在直角梯形PCDQ中,PQ2=CD2+(DQ-CP)2,解得t=.
∵<5,
因此,当t=时,以PQ为直径的圆与CD相切.
2.四边形ABCD是边长为2的正方形,E是AB的中点,连接DE,F是射线BC上一动点(不与点B重合),连接AF,交DE于点G.
(1)如图1,当F是BC的中点时,求证:△ABF≌△DAE.
(2)如图2,当点F与点C重合时,求AG的长.
(3)在点F运动的过程中,当线段BF为何值时,AG=AE?请说明理由.
(1)证明:∵四边形ABCD是正方形,∴∠B=∠DAE=90°,
AB=AD=BC.
∵E,F分别是AB,BC的中点,∴AE=BC.∴AE=BF.
在△ABF和△PAE中,
∴△ABF≌△DAE(SAS).
(2)解:∵在正方形ABCD中,AB∥CD,∠ADC=90°,
AD=CD=2,
∴AC=.∵AB∥CD,
∴△AGE∽△CGD.
∴.
(3)解:当BF=时,AG=AE.理由如下:如图,设AF交CD于点M.
若使AG=AE=1,则有∠1=∠2,∵AB∥CD,∴∠1=∠4.
又∵∠2=∠3,∴∠3=∠4.∴DM=MG.
在Rt△ADM中,AM2-DM2=AD2,即(DM+1)2-DM2=22,
解得DM=∴.
∵AB∥CD,∴△ABF∽△MCF.
∴.
解得BF=∴时,AG=AE.
3.如图1,在等腰直角三角形ADC中,∠ADC=90°,AD=4. E是AD的中点,以DE为边作正方形DEFG,连接AG,CE. 将正方形DEFG绕点D顺时针旋转,旋转角为α(0°<α<90°).
(1)如图2,在旋转过程中,
①判断△AGD与△CED是否全等,并说明理由.
②当CE=CD时,AG与EF交于点H,求GH的长.
(2)如图3,延长CE交直线AG于点P.
①求证:AG⊥CP.
②在旋转过程中,线段PC的长度是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(1)解:①△AGD≌△CED. 理由如下:∵四边形EFGD是正方形,
∴DG=DE,∠GDE=90°.
∵DA=DC,∠ADC=90°,∴∠GDE=∠ADC.
∴∠GDE-∠ADE=∠ADC-∠ADE,即∠ADG=∠CDE.
在△AGD和△CED中,
∴△AGD≌△CED(SAS).
②如图1,过点A作AT⊥GD于点T.∵△AGD≌△CED,CD=CE,
∴AD=AG=4.∵AT⊥GD,∴TG=TD=1.
∴AT=.
∵EF∥DG,∴∠GHF=∠AGT.∵∠F=∠ATG=90°,∴△GFH∽△ATG.
∴ ∴
∴.
(2)①证明:如图2,设AD交PC于点O.
∵△AGD≌△CED,∴∠DAG=∠DCE.
∵∠DCE+∠COD=90°,∠COD=∠AOP,
∴∠AOP+∠DAG=90°.
∴∠APO=90°.∴CP⊥AG.
②解:∵∠CPA=90°,AC是定值,
∴当∠ACP最小时,PC的值最大.
∴当DE⊥PC时,∠ACP的值最小,此时PC的值最大,此时点F与点P重合(如图3所示).
∵∠CED=90°,CD=4,DE=2,
∴EC=.
∵EF=DE=2,∴CP=CE+EF=2+2.
∴PC的最大值为2+2.
中考演练
ZHONG KAO YAN LIAN
PART THREE
03
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
【例】(2022·南沙一模)如图1,在正方形ABCD中,E为AD边上的一点,连接CE,过点D作DF⊥CE于点G,DF交AB于点F.已知DG=4,CG=16.
(1)EG的长是 1 ;
(2)如图2,以点G为圆心,GD为半径的圆与线段DF,CE分别交于M,N两点.
①连接CM,BM,若P为BM的中点,连接CP,
求证:∠BCP=∠MCP;
②连接BN,若Q为BN的中点,连接CQ,求线段CQ的长.
(2)①证明:连接CM,BM,CP.
∵G为DM的中点,CG⊥DM,∴CM=CD.
∵CD=CB,∴CB=CM.
∵P为BM的中点,∴∠BCP=∠MCP.
②解:过点Q作QH⊥CD于点H,
连接NH并延长交BC的延长线于点L,
过点N作NK⊥CD于点K.
在Rt△CGD中,DG=4,CG=16,
则CD=.
∵CG=16,GN=4,∴CN=16-4=12.
∵∠CGD=∠CKN=90°,∠NCK=∠DCG,
∴△CKN ∽△CGD.
∴.
解得CK=.
∵QH⊥CD,∠DCB=90°,
NK⊥CD,
∴NK∥QH∥BC.
∵NQ=QB,
∴KH=HC=.
易证QH=.
∴CQ=.
模拟演练
MO NI YAN LIAN
PART FOUR
04
SPORT
2024
题型突破
中考演练
思维指导
模拟演练
1.如图1,在等腰三角形ABC中,∠A=120°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接BE,M,N,P分别为DE,BE,BC的中点.
(1)【观察猜想】
图1中,线段NM,NP的数量关系是 ,∠MNP的度数为 ;
60°
NM=NP
(2)【探究证明】
把△ADE绕点A顺时针方向旋转到如图2所示的位置,连接MP,BD,CE,判断△MNP的形状,并说明理由;
(3)【拓展延伸】
把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请求出△MNP面积的最大值.
(2)解:△MNP是等边三角形.理由如下:
由旋转可得,∠BAD=∠CAE.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS).
∴BD=CE,∠ABD=∠ACE.
∵M,N,P分别为DE,BE,BC的中点.
∴MN=CE,MN∥BD,PN∥CE.
∴MN=PN,∠ENM=∠EBD,∠BPN=∠BCE.
∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB.
∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE=∠ENM,
∴∠MNP=∠ENP+∠ENM=(∠EBC+∠ACE)+(∠ABE+∠ECB)=180°-∠BAC=60°.
∴△MNP是等边三角形.
(3)根据题意,得BD≤AB+AD,即BD≤4.∴MN≤2.
∴△MNP的面积=MN2.
∴△MNP的面积的最大值为.
2.如图1,四边形ABCD的对角线AC,BD相交于点O,OA=OC,
OB=OD+CD.
(1)过点A作AE∥DC交BD于点E,
①求证:△AOE≌△COD;
②求证:AE=BE;
(2)如图2,将△ABD沿AB翻折得到△ABD',若AD'∥BC,
求证:CD2=2OD·BD.
证明:(1)①∵AE∥DC,
∴∠CDO=∠AEO,∠DCO=∠EAO.
在△AOE和△COD中,
∴△AOE≌△COD(AAS).
②∵△AOE≌△COD,∴CD=AE,OD=OE.
∵OB=OE+BE,OB=OD+CD,
∴BE=CD. ∴AE=BE.
(2)过点A作AF∥DC交BD于点E,交BC于点F.
∵AD'∥BC,∴∠D'AB=∠ABC.
由翻折可知,∠D'AB=∠DAB,∴∠ABC=∠DAB.
∵AE=BE,∴∠ABD=∠EAB.
∴∠ABC-∠ABD=∠DAB-∠EAB,
即∠DBC=∠DAE.
∵AE∥DC,∴∠AED=∠CDB. ∴△ADE∽△BCD.
∴.∴AE·CD=DE·BD.
由②可知,AE=CD,OD=EO.
∴DE=2OD.∴CD2=2OD·BD.
3.(2022·南沙一模)如图,在△ABC中,∠ABC=90°,过点B作BD⊥AC于点D.
(1)尺规作图:作边BC的垂直平分线,交边AC于点E;
(2)若AD∶BD=3∶4,求sin C的值;
(3)已知BC=10,BD=6.若点P为平面内任意一动点,且保持∠BPC=90°,求线段AP的最大值.
解:(1)如图1即为所求,
(2)设AD=3x,BD=4x.
∴AB==5x.
∵∠ABC=90°,∴∠ABD+∠DBC=90°.
∵BD⊥AC,∴∠DBC+∠C=90°.
∴∠C=∠ABD.
∴sin C=sin∠ABD=.
(3)如图2,以BC为直径作圆O,连接AO交圆于两点P1,P2,
当P与P2重合时,AP取最大值AP2.连接BP1,BP2.
∵sin∠ABD=,
∴sin∠BAD=
∴.
在Rt△ABO中,AO2=AB2+OB2.
∴AO=.
∴线段AP的最大值是AP2=+5.
同课章节目录
