21.2 二次函数y=ax?的图象和性质(第1课时) 课件(共61张PPT)
文档属性
| 名称 | 21.2 二次函数y=ax?的图象和性质(第1课时) 课件(共61张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 20:36:24 | ||
图片预览





文档简介
(共61张PPT)
九年级沪科版数学上册 第二十一章二次函数与反比例函数
21.2 二次函数的图象和性质
第一课时 二次函数y=ax 的图象和性质
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.正确理解抛物线的有关概念.(重点)
2.会用描点法画出二次函数y=ax 的图象,概括出图象的特点.(难点)
3.掌握形如y=ax 的二次函数图象的性质,并会应用.(难点)
情景导入
探究二次函数 y=ax2 的图象和性质
课本例1.画出二次函数 y=x2 的图象.
观察y=x2的表达式,选择适当x值,并计算相应的y值.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
1.列表
你会用描点法画二次函数y=x2的图象吗
新知探究
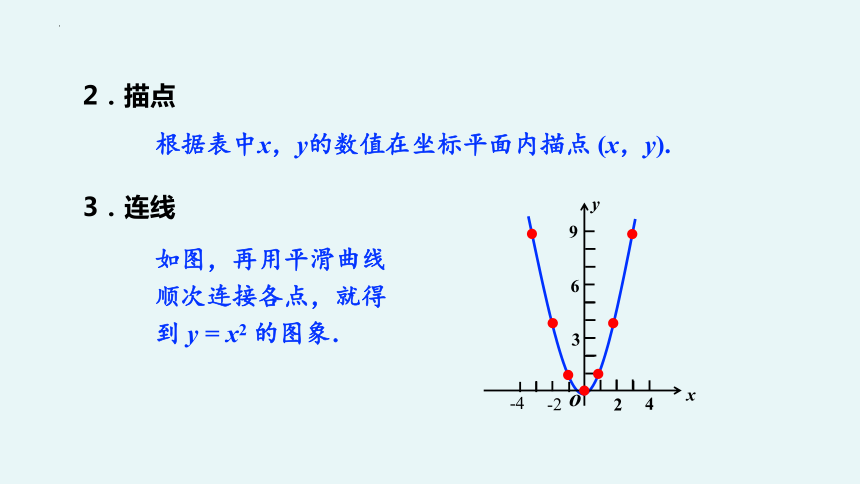
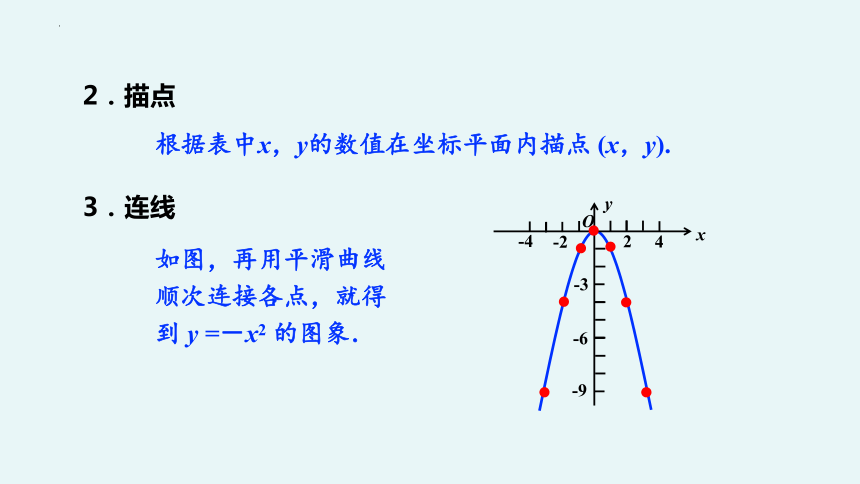
2.描点
根据表中x,y的数值在坐标平面内描点 (x,y).
3.连线
如图,再用平滑曲线顺次连接各点,就得到 y = x2 的图象.
2
4
-2
-4
o
3
6
9
x
y
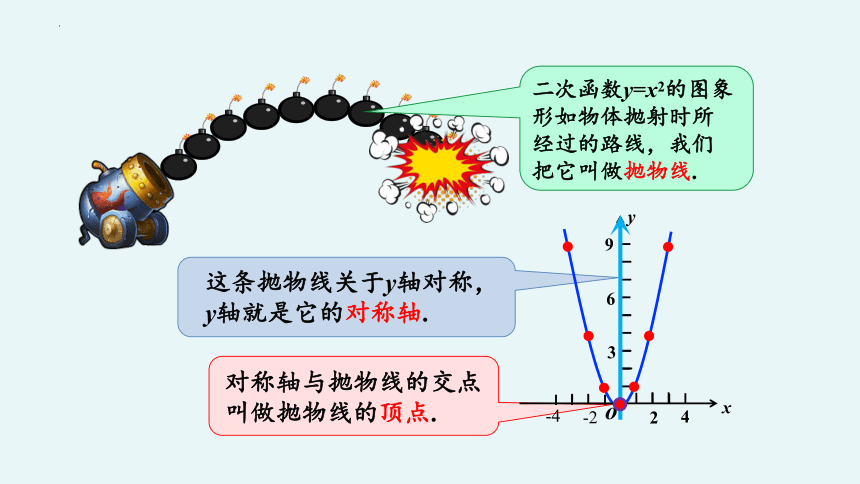
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
2
4
-2
-4
o
3
6
9
x
y
1
4
-1
-3
O
1
x
y
-2
-4
3
2
2
3
4
5
6
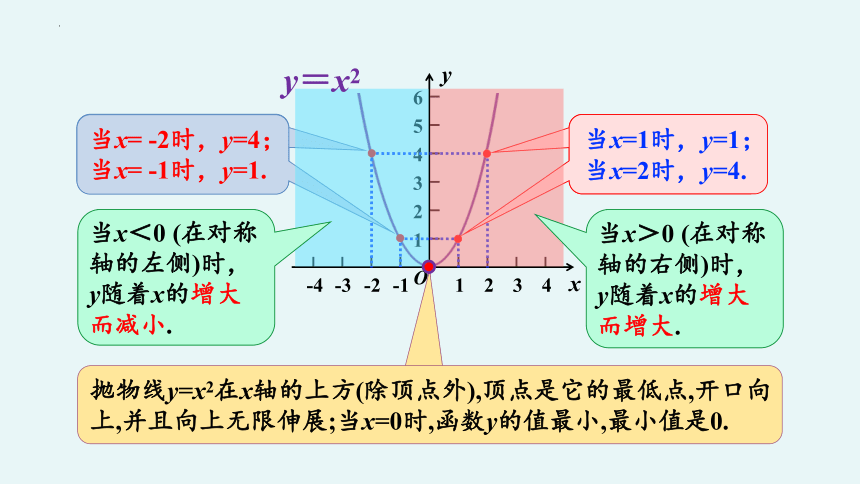
当x= -2时,y=4;
当x= -1时,y=1.
当x=1时,y=1;
当x=2时,y=4.
y=x2
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时,y随着x的增大而增大.
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
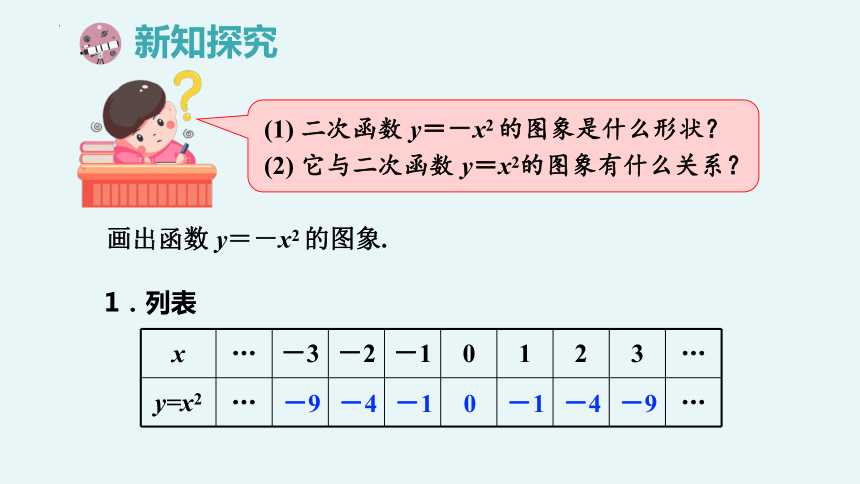
画出函数 y=-x2 的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
-9
-4
-1
0
-1
-9
-4
1.列表
(1) 二次函数 y=-x2 的图象是什么形状?
(2) 它与二次函数 y=x2的图象有什么关系?
新知探究
2.描点
根据表中x,y的数值在坐标平面内描点 (x,y).
3.连线
如图,再用平滑曲线顺次连接各点,就得到 y =-x2 的图象.
y
2
4
-2
-4
O
-3
-6
-9
x
1
4
-1
-3
O
-5
x
y
-2
-4
3
2
-4
-3
-2
-1
-6
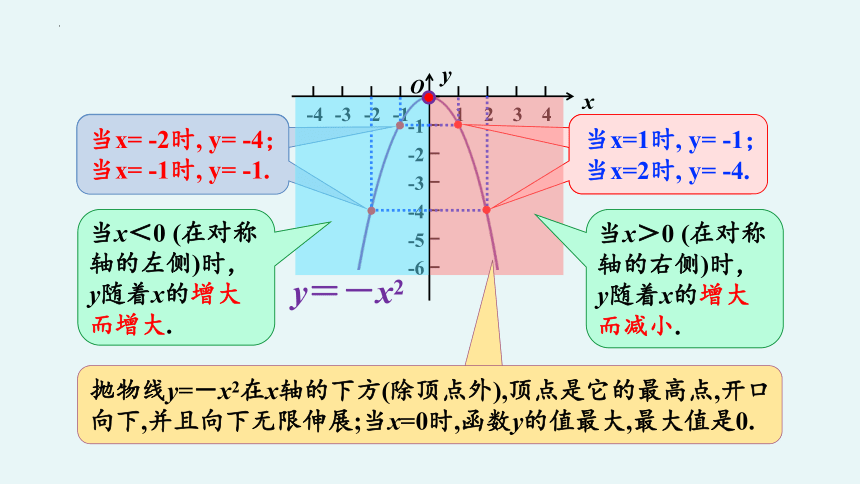
当x= -2时, y= -4;
当x= -1时, y= -1.
当x=1时, y= -1;
当x=2时, y= -4.
y=-x2
当x<0 (在对称轴的左侧)时,y随着x的增大而增大.
当x>0 (在对称轴的右侧)时,y随着x的增大而减小.
抛物线y=-x2在x轴的下方(除顶点外),顶点是它的最高点,开口向下,并且向下无限伸展;当x=0时,函数y的值最大,最大值是0.
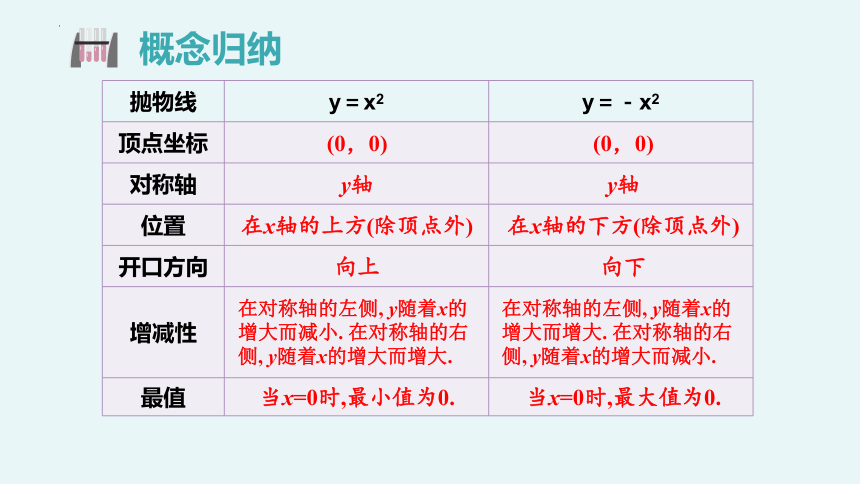
抛物线 y=x2 y=-x2
顶点坐标
对称轴
位置
开口方向
增减性
最值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧, y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧, y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
概念归纳
例2.在同一直角坐标系中,画出函数 y= x2 ,y=2x2 的图象.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2 … …
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2 … …
列表
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
课本例题
描点、连线
如图,即得这两个函数的图象.
-2
2
2
4
6
4
-4
8
O
x
y
y=2x2
y= x2
y=x2
如图可知,当 a>0 时,a 越大,开口越小.
1.在同一直角坐标系中,画出函数 y=- x2 ,y=-2x2
的图象.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= - x2 … …
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y= -2x2 … …
列表
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
练一练
描点、连线
如图,即得这两个函数的图象.
-2
2
-2
-4
-6
4
-4
-8
x
y
O
y=- x2
y=-2x2
y=-x2
如图可知,当a<0时,a 越大,开口越大.
y=ax2 a>0 a<0
图象
位置开 口方向
对称性 顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
概念归纳
3.函数y= x2的图象的开口 ,对称轴是 ,
顶点是 ;顶点是抛物线的最 点
2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 顶点是抛物线的最 点
1.函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
4.函数y= -0.2x2的图象的开口 ,对称轴是___,顶点是 ;
向上
y轴
(0,0)
向下
y轴
(0,0)
高
低
练一练
例 3: 已知 y =(m+1)x 是二次函数,且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2.
典例剖析
例 4 :已知二次函数y=x2.
(1)判断点A(2,4)在二次函数图象上吗?
(2)请分别写出点A关于x轴的对称点B的坐标,关于y轴的对称点C的坐标,关于原点O的对称点D的坐标;
(3)点B、C、D在二次函数y=x2的图象上吗?在二次函数y=-x2的图象上吗?
典例剖析
(1)判断点A(2,4)在二次函数图象上吗?
解:(1)当x=2时,y=x2=4,
所以A(2,4)在二次函数图象上;
(2)请分别写出点A关于x轴的对称点B的坐标,关于y轴的对称点C的坐标,关于原点O的对称点D的坐标;
(2)点A关于x轴的对称点B的坐标为(2,-4),点A关于y轴的对称点C的坐标为(-2,4),点A关于原点O的对称点D的坐标为(-2,-4);
(3)点B、C、D在二次函数y=x2的图象上吗?在二次函数y=-x2的图象上吗?
当x=-2时,y=x2=4,
所以C点在二次函数y=x2的图象上;
当x=2时,y=-x2=-4,
所以B点在二次函数y=-x2的图象上;
当x=-2时,y=-x2=-4,
所以D点在二次函数y=-x2的图象上.
已知 是二次函数,且当x>0时,y随x增大而增大,则k= .
分析: 是二次函数,即二次项的系数不为0,x的指数等于2.又因当x>0时,y随x增大而增大,即说明二次项的系数大于0.因此,
解得k=2
2
练一练
例 5. 已知二次函数y=2x2.
(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,
则 y1_____ y2;(填“>”“=”或“<”);
(2)如图,此二次函数的图象经过点(0,0),长方形
ABCD的顶点A、B在x轴上,C、D恰好在二次函数的
图象上,B点的横坐标为2,求图中阴影部分的面积
之和.
<
典例剖析
(2)解:∵二次函数y=2x2的图象经过点B,
∴当x=2时,y=2×22=8.
∵抛物线和长方形都是轴对称图形,且y轴为它
们的对称轴,
∴OA=OB,
∴在长方形ABCD内,左边阴影部分面积等于右边空白部分面积,
∴S阴影部分面积之和=2×8=16.
二次函数y=ax2的图象关于y轴对称,因此左右两部分折叠可以重合,在二次函数比较大小中,我们根据图象中点具有的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较;对于求不规则的图形面积,采用等面积割补法,将不规则图形转化为规则图形以方便求解.
总结归纳
1.函数y=2x2的图象的开口 ,
对称轴 ,顶点是 ;
在对称轴的左侧,y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .
2.函数y=-3x2的图象的开口 ,
对称轴 ,顶点是 ;
在对称轴的左侧, y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .
向上
向下
y轴
y轴
(0,0)
(0,0)
减小
减小
增大
增大
x
x
y
y
O
O
练一练
3.已知二次函数y=x2,若x≥m时,y最小值为0,求实数m的取值范围.
解:∵二次函数y=x2,
∴当x=0时,y有最小值,且y最小值=0,
∵当x≥m时,y最小值=0,
∴m≤0.
练一练
4.已知:如图,直线y=3x+4与抛物线y=x2交于A、B两点,求出A、B两点的坐标,并求出两交点与原点所围成的三角形的面积.
解:由题意得
解得
所以此两函数的交点坐标为A(4,16)和B(-1,1).
∵直线y=3x+4与y轴相交于点C(0,4),即CO=4.
∴S△ACO= ·CO·4=8,S△BOC= ×4×1=2,
∴S△ABO=S△ACO+S△BOC=10.
练一练
课本练习
1.(1)在同一平面直角坐标系中,画出画数的图象;
-2 -1 0 1 2
0
12 3 0 3 12
0
-12 -3 0 -3 -12
解:(1)描点、连线,即得函数图象,如图所示.
(2)观察上述图象,并说出图象的顶点坐标、开口方向、对称轴;
(3)说出各图象中的最高点或最低点的坐标;
解:(2)由图象可知,函数,的开口都向上,对称轴都是y轴,顶点坐标为(0,0),抛物线,的开口向下,对称轴是y轴,顶点坐标为(0,0).
解:(3)由图象可知,函数,都有最低点,当x=0时, 0,所以最低点坐标为(0,0),函数,都有最高点,当x=0时, 0,所以最高点坐标为(0,0).
解:(4)由图象可知,函数,的图象在x<0时,y随x的增大而减小,在x>0时,y随x的增大而增大,函数,的图象,在x<0时,y随x的增大而增大,在x>0时,y随x的增大而减小.
(4)说明各函数图象在对称轴两侧部分,函数y随x增大而变化的情况.
课本练习
2.在下列抛物线中,开口最大、最小的各是哪一个?
解:因为,所以抛物线的开口最大,抛物线 的开口最小.
课本练习
3,在同一平面直角坐标系中,下列各组中两个函数的图象有怎样的位置关系?
(1)与 y;(2)与;
(3)与.
解:(1)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
(2)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
(3)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
课本练习
4.画出函数的图象,并根据图象求:
(1)当 x=2,-1.7 时的 y 值(精确到 0.1);
(2)当y =2,5.8时的 x 值(精确到 0.1);
(3)图象上最低点的坐标.
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
在平面直角坐标系中描点,然后用平滑的曲线连接,得图象,如图所示.
由图象可知:
(1)当x=2时,y=4.0;当x=-1.7时,y=2.9.
(2)当y=2时,x=±1.4;当y=5.8时,x=±2.4.
(3)(0,0).
课本练习
5.二次函数的图象经过点(2,-2).
(1)求这个函数的表达式;
(2)当x为何值时,函数y随x的增大而增大?
解:(1)把点(2,-2)代人,解得,所以这个二次函数的表达式为.
(2)因为的顶点坐标是(0,0),开口向下,所以当x<0时,y随x的增大而增大.
y轴(或x=0)
(0,0)
上
最小
下
最大
|a|
小
大
C
分层练习-基础
D
m<2
不同
相同
相同
相同
x轴
y1>y2>y3
分层练习-基础
减小
增大
最小
0
增大
减小
最大
0
B
分层练习-基础
C
>
m>0
分层练习-基础
0
a<-1
-4
±2
分层练习-基础
分层练习-基础
分层练习-基础
D
B
3
分层练习-巩固
2
③
②
①
④
分层练习-巩固
2π
分层练习-巩固
分层练习-巩固
分层练习-巩固
C
B
分层练习-巩固
C
D
4
-4
0
0
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
-2
课堂反馈
课堂反馈
C
课堂反馈
0
0
4
8
课堂反馈
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
课堂小结
九年级沪科版数学上册 第二十一章二次函数与反比例函数
21.2 二次函数的图象和性质
第一课时 二次函数y=ax 的图象和性质
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1.正确理解抛物线的有关概念.(重点)
2.会用描点法画出二次函数y=ax 的图象,概括出图象的特点.(难点)
3.掌握形如y=ax 的二次函数图象的性质,并会应用.(难点)
情景导入
探究二次函数 y=ax2 的图象和性质
课本例1.画出二次函数 y=x2 的图象.
观察y=x2的表达式,选择适当x值,并计算相应的y值.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
9
4
1
0
1
9
4
1.列表
你会用描点法画二次函数y=x2的图象吗
新知探究
2.描点
根据表中x,y的数值在坐标平面内描点 (x,y).
3.连线
如图,再用平滑曲线顺次连接各点,就得到 y = x2 的图象.
2
4
-2
-4
o
3
6
9
x
y
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,y轴就是它的对称轴.
对称轴与抛物线的交点叫做抛物线的顶点.
2
4
-2
-4
o
3
6
9
x
y
1
4
-1
-3
O
1
x
y
-2
-4
3
2
2
3
4
5
6
当x= -2时,y=4;
当x= -1时,y=1.
当x=1时,y=1;
当x=2时,y=4.
y=x2
当x<0 (在对称轴的左侧)时,y随着x的增大而减小.
当x>0 (在对称轴的右侧)时,y随着x的增大而增大.
抛物线y=x2在x轴的上方(除顶点外),顶点是它的最低点,开口向上,并且向上无限伸展;当x=0时,函数y的值最小,最小值是0.
画出函数 y=-x2 的图象.
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
-9
-4
-1
0
-1
-9
-4
1.列表
(1) 二次函数 y=-x2 的图象是什么形状?
(2) 它与二次函数 y=x2的图象有什么关系?
新知探究
2.描点
根据表中x,y的数值在坐标平面内描点 (x,y).
3.连线
如图,再用平滑曲线顺次连接各点,就得到 y =-x2 的图象.
y
2
4
-2
-4
O
-3
-6
-9
x
1
4
-1
-3
O
-5
x
y
-2
-4
3
2
-4
-3
-2
-1
-6
当x= -2时, y= -4;
当x= -1时, y= -1.
当x=1时, y= -1;
当x=2时, y= -4.
y=-x2
当x<0 (在对称轴的左侧)时,y随着x的增大而增大.
当x>0 (在对称轴的右侧)时,y随着x的增大而减小.
抛物线y=-x2在x轴的下方(除顶点外),顶点是它的最高点,开口向下,并且向下无限伸展;当x=0时,函数y的值最大,最大值是0.
抛物线 y=x2 y=-x2
顶点坐标
对称轴
位置
开口方向
增减性
最值
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方(除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧, y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧, y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
概念归纳
例2.在同一直角坐标系中,画出函数 y= x2 ,y=2x2 的图象.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= x2 … …
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y=2x2 … …
列表
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
课本例题
描点、连线
如图,即得这两个函数的图象.
-2
2
2
4
6
4
-4
8
O
x
y
y=2x2
y= x2
y=x2
如图可知,当 a>0 时,a 越大,开口越小.
1.在同一直角坐标系中,画出函数 y=- x2 ,y=-2x2
的图象.
x … -4 -3 -2 -1 0 1 2 3 4 …
y= - x2 … …
x … -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 …
y= -2x2 … …
列表
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
-8
-4.5
-2
-0.5
0
-8
-4.5
-2
-0.5
练一练
描点、连线
如图,即得这两个函数的图象.
-2
2
-2
-4
-6
4
-4
-8
x
y
O
y=- x2
y=-2x2
y=-x2
如图可知,当a<0时,a 越大,开口越大.
y=ax2 a>0 a<0
图象
位置开 口方向
对称性 顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于y轴对称,对称轴是直线x=0
顶点坐标是原点(0,0)
当x=0时,y最小值=0
当x=0时,y最大值=0
在对称轴左侧递减
在对称轴右侧递增
在对称轴左侧递增
在对称轴右侧递减
y
O
x
y
O
x
概念归纳
3.函数y= x2的图象的开口 ,对称轴是 ,
顶点是 ;顶点是抛物线的最 点
2.函数y=-3x2的图象的开口 ,对称轴是 ,顶点是 顶点是抛物线的最 点
1.函数y=4x2的图象的开口 ,对称轴是 ,顶点是 ;
向上
向下
y轴
y轴
(0,0)
(0,0)
4.函数y= -0.2x2的图象的开口 ,对称轴是___,顶点是 ;
向上
y轴
(0,0)
向下
y轴
(0,0)
高
低
练一练
例 3: 已知 y =(m+1)x 是二次函数,且其图象开口向上,求m的值和函数解析式
m2+m
解: 依题意有:
m+1>0 ①
m2+m=2 ②
解②得:m1=-2, m2=1
由①得:m>-1
∴ m=1
此时,二次函数为: y=2x2.
典例剖析
例 4 :已知二次函数y=x2.
(1)判断点A(2,4)在二次函数图象上吗?
(2)请分别写出点A关于x轴的对称点B的坐标,关于y轴的对称点C的坐标,关于原点O的对称点D的坐标;
(3)点B、C、D在二次函数y=x2的图象上吗?在二次函数y=-x2的图象上吗?
典例剖析
(1)判断点A(2,4)在二次函数图象上吗?
解:(1)当x=2时,y=x2=4,
所以A(2,4)在二次函数图象上;
(2)请分别写出点A关于x轴的对称点B的坐标,关于y轴的对称点C的坐标,关于原点O的对称点D的坐标;
(2)点A关于x轴的对称点B的坐标为(2,-4),点A关于y轴的对称点C的坐标为(-2,4),点A关于原点O的对称点D的坐标为(-2,-4);
(3)点B、C、D在二次函数y=x2的图象上吗?在二次函数y=-x2的图象上吗?
当x=-2时,y=x2=4,
所以C点在二次函数y=x2的图象上;
当x=2时,y=-x2=-4,
所以B点在二次函数y=-x2的图象上;
当x=-2时,y=-x2=-4,
所以D点在二次函数y=-x2的图象上.
已知 是二次函数,且当x>0时,y随x增大而增大,则k= .
分析: 是二次函数,即二次项的系数不为0,x的指数等于2.又因当x>0时,y随x增大而增大,即说明二次项的系数大于0.因此,
解得k=2
2
练一练
例 5. 已知二次函数y=2x2.
(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,
则 y1_____ y2;(填“>”“=”或“<”);
(2)如图,此二次函数的图象经过点(0,0),长方形
ABCD的顶点A、B在x轴上,C、D恰好在二次函数的
图象上,B点的横坐标为2,求图中阴影部分的面积
之和.
<
典例剖析
(2)解:∵二次函数y=2x2的图象经过点B,
∴当x=2时,y=2×22=8.
∵抛物线和长方形都是轴对称图形,且y轴为它
们的对称轴,
∴OA=OB,
∴在长方形ABCD内,左边阴影部分面积等于右边空白部分面积,
∴S阴影部分面积之和=2×8=16.
二次函数y=ax2的图象关于y轴对称,因此左右两部分折叠可以重合,在二次函数比较大小中,我们根据图象中点具有的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较;对于求不规则的图形面积,采用等面积割补法,将不规则图形转化为规则图形以方便求解.
总结归纳
1.函数y=2x2的图象的开口 ,
对称轴 ,顶点是 ;
在对称轴的左侧,y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .
2.函数y=-3x2的图象的开口 ,
对称轴 ,顶点是 ;
在对称轴的左侧, y随x的增大而 ,
在对称轴的右侧, y随x的增大而 .
向上
向下
y轴
y轴
(0,0)
(0,0)
减小
减小
增大
增大
x
x
y
y
O
O
练一练
3.已知二次函数y=x2,若x≥m时,y最小值为0,求实数m的取值范围.
解:∵二次函数y=x2,
∴当x=0时,y有最小值,且y最小值=0,
∵当x≥m时,y最小值=0,
∴m≤0.
练一练
4.已知:如图,直线y=3x+4与抛物线y=x2交于A、B两点,求出A、B两点的坐标,并求出两交点与原点所围成的三角形的面积.
解:由题意得
解得
所以此两函数的交点坐标为A(4,16)和B(-1,1).
∵直线y=3x+4与y轴相交于点C(0,4),即CO=4.
∴S△ACO= ·CO·4=8,S△BOC= ×4×1=2,
∴S△ABO=S△ACO+S△BOC=10.
练一练
课本练习
1.(1)在同一平面直角坐标系中,画出画数的图象;
-2 -1 0 1 2
0
12 3 0 3 12
0
-12 -3 0 -3 -12
解:(1)描点、连线,即得函数图象,如图所示.
(2)观察上述图象,并说出图象的顶点坐标、开口方向、对称轴;
(3)说出各图象中的最高点或最低点的坐标;
解:(2)由图象可知,函数,的开口都向上,对称轴都是y轴,顶点坐标为(0,0),抛物线,的开口向下,对称轴是y轴,顶点坐标为(0,0).
解:(3)由图象可知,函数,都有最低点,当x=0时, 0,所以最低点坐标为(0,0),函数,都有最高点,当x=0时, 0,所以最高点坐标为(0,0).
解:(4)由图象可知,函数,的图象在x<0时,y随x的增大而减小,在x>0时,y随x的增大而增大,函数,的图象,在x<0时,y随x的增大而增大,在x>0时,y随x的增大而减小.
(4)说明各函数图象在对称轴两侧部分,函数y随x增大而变化的情况.
课本练习
2.在下列抛物线中,开口最大、最小的各是哪一个?
解:因为,所以抛物线的开口最大,抛物线 的开口最小.
课本练习
3,在同一平面直角坐标系中,下列各组中两个函数的图象有怎样的位置关系?
(1)与 y;(2)与;
(3)与.
解:(1)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
(2)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
(3)和的图象形状相同,顶点相同,对称轴相同,开口方向相反,两图象关于x轴对称.
课本练习
4.画出函数的图象,并根据图象求:
(1)当 x=2,-1.7 时的 y 值(精确到 0.1);
(2)当y =2,5.8时的 x 值(精确到 0.1);
(3)图象上最低点的坐标.
-3 -2 -1 0 1 2 3
9 4 1 0 1 4 9
在平面直角坐标系中描点,然后用平滑的曲线连接,得图象,如图所示.
由图象可知:
(1)当x=2时,y=4.0;当x=-1.7时,y=2.9.
(2)当y=2时,x=±1.4;当y=5.8时,x=±2.4.
(3)(0,0).
课本练习
5.二次函数的图象经过点(2,-2).
(1)求这个函数的表达式;
(2)当x为何值时,函数y随x的增大而增大?
解:(1)把点(2,-2)代人,解得,所以这个二次函数的表达式为.
(2)因为的顶点坐标是(0,0),开口向下,所以当x<0时,y随x的增大而增大.
y轴(或x=0)
(0,0)
上
最小
下
最大
|a|
小
大
C
分层练习-基础
D
m<2
不同
相同
相同
相同
x轴
y1>y2>y3
分层练习-基础
减小
增大
最小
0
增大
减小
最大
0
B
分层练习-基础
C
>
m>0
分层练习-基础
0
a<-1
-4
±2
分层练习-基础
分层练习-基础
分层练习-基础
D
B
3
分层练习-巩固
2
③
②
①
④
分层练习-巩固
2π
分层练习-巩固
分层练习-巩固
分层练习-巩固
C
B
分层练习-巩固
C
D
4
-4
0
0
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
-2
课堂反馈
课堂反馈
C
课堂反馈
0
0
4
8
课堂反馈
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
重点关注4个方面
开口方向及大小
对称轴
顶点坐标
增减性
课堂小结
