第20章 数据的分析复盘提升(单元复习课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 第20章 数据的分析复盘提升(单元复习课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 24.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
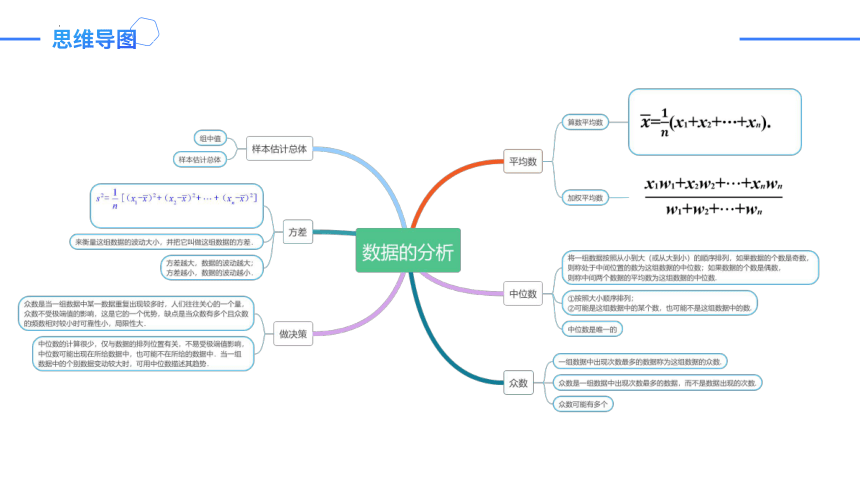
思维导图
知识串讲
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
知识串讲
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
知识串讲
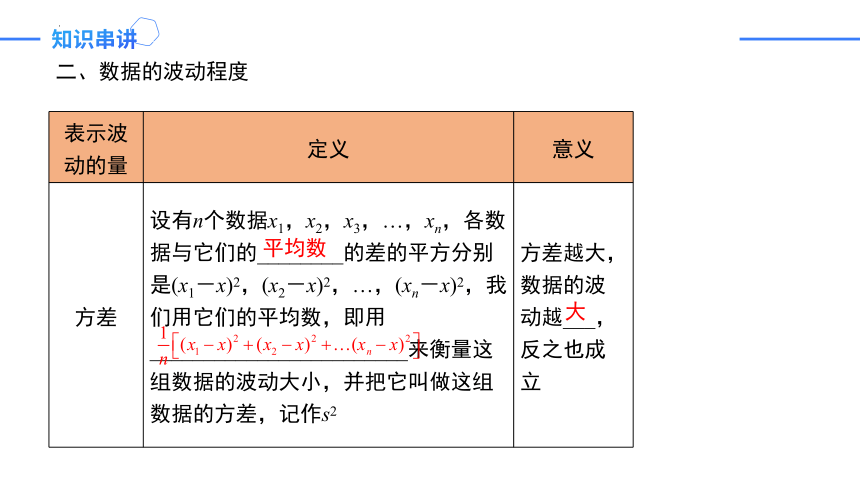
二、数据的波动程度
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
知识串讲
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
考点梳理
考点一:平均数、中位数、众数
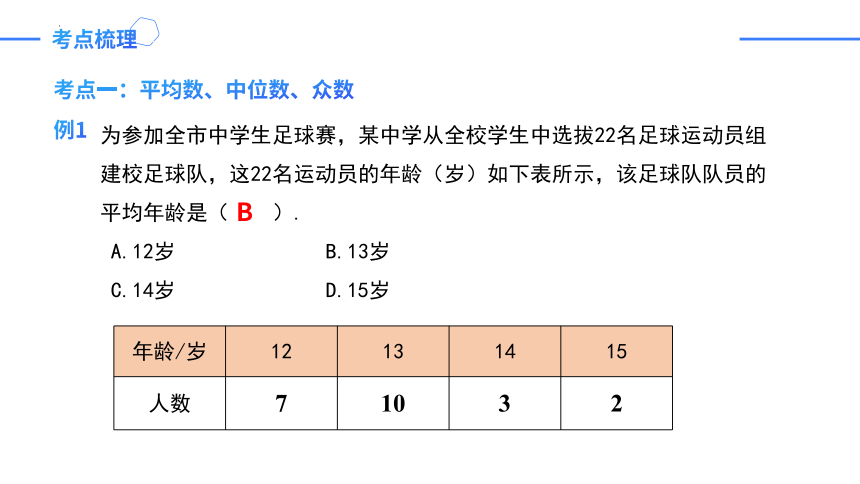
例1
为参加全市中学生足球赛,某中学从全校学生中选拔22名足球运动员组建校足球队,这22名运动员的年龄(岁)如下表所示,该足球队队员的平均年龄是( ).
A.12岁 B.13岁
C.14岁 D.15岁
年龄/岁 12 13 14 15
人数 7 10 3 2
B
考点梳理
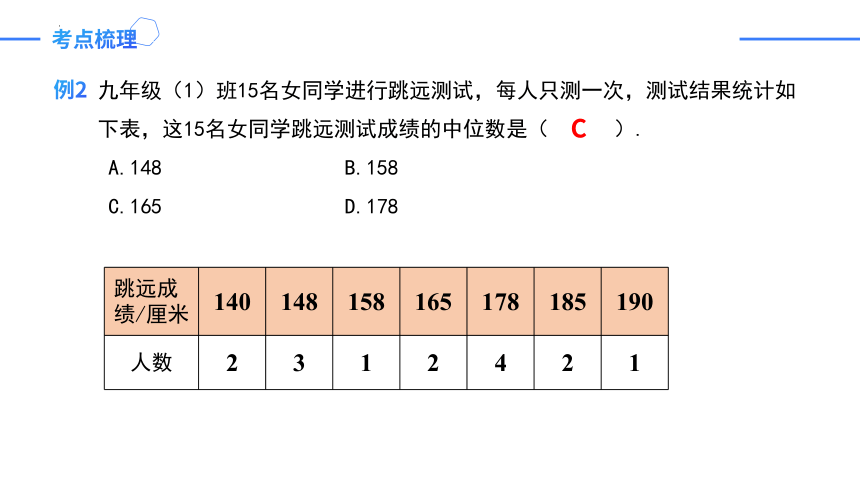
例2
九年级(1)班15名女同学进行跳远测试,每人只测一次,测试结果统计如下表,这15名女同学跳远测试成绩的中位数是( ).
A.148 B.158
C.165 D.178
跳远成绩/厘米 140 148 158 165 178 185 190
人数 2 3 1 2 4 2 1
C
考点梳理
例3
某单位组织职工开展植树活动,植树量与人数之间的关系如图,
下列说法不正确的是( ).
D
A.共有30人参加本次植树活动
B.每人植树量的众数为4棵
C.每人植树量的中位数是5棵
D.每人植树量的平均数是5棵
考点梳理
例4
C
如图为某班35名学生投篮成绩的条形统计图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5.则根据图形无法确定下列哪一选项中的数值.( )
0
2
4
6
8
10
A.4球以下的人数
B.5球以下的人数
C.6球以下的人数
D.7球以下的人数
1
2
3
4
5
6
7
投篮成绩
人数
刻意练习
练1
已知一组数据3,5,6,7,5.则其平均数为_____;
中位数是______;众数是_____.
某校4个绿化小组一天的植树棵树如下:8,10,x,10,已知这组数据的众数与平均数相同,则这组数据的中位数是_____.
5.2
5
5
10
练3
5
练2
刻意练习
练4
已知数据 3、5、6、x、7、2、8、4 的平均数是 5,求出这组数据的中位数和众数.
解:这组数据的平均数=5,
解得 x=5.
将这组数据从小到大排列得:2、3、4、5、5、6、7、8,
中位数为5,众数为5.
考点梳理
例1
12
一组数据6,4,a,3,2的平均数是4,则这组数据的方差为____.
学校为了选拔4名播音员,对20名学生进行了两次普通话测试,满分为10分.统计得,第一次测试的方差为1.2275分 ,第二次方差为1.3475分 .则第___次的测试结果对选拔播音员更要参考意义.
2
二
例2
例3
考点二:方差
考点梳理
例4
下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择____.
185
3.6
180
3.6
乙
甲
丙
丁
平均数(cm)
方差(cm )
180
185
7.4
8.1
甲
考点梳理
考点三:分析数据做决策
例1
生物工作者为了估计小山上山雀的数量,先捕了20只做上标记后放还,一星期后,又捕捉了40只山雀,发现带标记的有2只,由此估计小山上的山雀有____只.
400
考点梳理
例2
甲校和乙校九年级学生各有300名.为了解这两个学校九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据.从两个学校九年级中各随机抽取10名学生,进行英语单词测试.
成绩如下:(百分制,单位:分)
甲校:92 100 86 89 73 98 54 95 98 85
乙校:100 100 94 83 74 86 75 100 73 75
②根据数据,填写下表:
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
考点梳理
例2
(1)若成绩90分以上为优秀估计乙校九年级学生英语单词掌握优秀的人数.
300×40%=120
解:样本容量为10的样本中,优秀的人数为4,可得样本中的优秀率为40%,据此推断总体中优秀率为40%.
因此乙校九年级学生英语单词掌握优秀的人数为120.
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
考点梳理
例2
(2)你认为那个学校的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性).
解:乙校的九年级学生英语单词掌握得比较好.
理由:①乙校的九年级学生英语单词测试中,平均分高于甲校;②乙校的九年级学生在英语单词测试中,中位数较高,说明乙校英语单词测试成绩分数高的学生较多.
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
刻意练习
练1
某公司 33 名职工的月工资(以元为单位)如下:
(1)求该公司职工月工资的平均数、中位数、众数.(精确到个位)
职工 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
解析:(1)平均数
(元)
把这 33 个数据按照从小到大的顺序可得中位数为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了 20 次,所以众数为 1500.
刻意练习
练1
(2)假设副董事长的工资从 5000 元提升到 20000 元,董事长的工资从 5500 元提升到 30000 元,那么新的平均数、中位数、众数又是什么?(精确到个位)
(2)新的平均数
(元)
把这 33 个数据按照从小到大的顺序可得新的中位数仍为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了20 次,
所以新的众数仍为 1500.
第20章
数据的分析
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
单元复盘提升
思维导图
知识串讲
一、数据的集中趋势
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平 均数 一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
知识串讲
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
知识串讲
二、数据的波动程度
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越___,反之也成立
知识串讲
三、用样本估计总体
1.统计的基本思想:用样本的特征(平均数和方差)估计总体的特征.
2.统计的决策依据:利用数据做决策时,要全面、多角度地去分析已有数据,从数据的变化中发现它们的规律和变化趋势,减少人为因素的影响.
考点梳理
考点一:平均数、中位数、众数
例1
为参加全市中学生足球赛,某中学从全校学生中选拔22名足球运动员组建校足球队,这22名运动员的年龄(岁)如下表所示,该足球队队员的平均年龄是( ).
A.12岁 B.13岁
C.14岁 D.15岁
年龄/岁 12 13 14 15
人数 7 10 3 2
B
考点梳理
例2
九年级(1)班15名女同学进行跳远测试,每人只测一次,测试结果统计如下表,这15名女同学跳远测试成绩的中位数是( ).
A.148 B.158
C.165 D.178
跳远成绩/厘米 140 148 158 165 178 185 190
人数 2 3 1 2 4 2 1
C
考点梳理
例3
某单位组织职工开展植树活动,植树量与人数之间的关系如图,
下列说法不正确的是( ).
D
A.共有30人参加本次植树活动
B.每人植树量的众数为4棵
C.每人植树量的中位数是5棵
D.每人植树量的平均数是5棵
考点梳理
例4
C
如图为某班35名学生投篮成绩的条形统计图,其中上面部分数据破损导致数据不完全,已知此班学生投篮成绩的中位数是5.则根据图形无法确定下列哪一选项中的数值.( )
0
2
4
6
8
10
A.4球以下的人数
B.5球以下的人数
C.6球以下的人数
D.7球以下的人数
1
2
3
4
5
6
7
投篮成绩
人数
刻意练习
练1
已知一组数据3,5,6,7,5.则其平均数为_____;
中位数是______;众数是_____.
某校4个绿化小组一天的植树棵树如下:8,10,x,10,已知这组数据的众数与平均数相同,则这组数据的中位数是_____.
5.2
5
5
10
练3
5
练2
刻意练习
练4
已知数据 3、5、6、x、7、2、8、4 的平均数是 5,求出这组数据的中位数和众数.
解:这组数据的平均数=5,
解得 x=5.
将这组数据从小到大排列得:2、3、4、5、5、6、7、8,
中位数为5,众数为5.
考点梳理
例1
12
一组数据6,4,a,3,2的平均数是4,则这组数据的方差为____.
学校为了选拔4名播音员,对20名学生进行了两次普通话测试,满分为10分.统计得,第一次测试的方差为1.2275分 ,第二次方差为1.3475分 .则第___次的测试结果对选拔播音员更要参考意义.
2
二
例2
例3
考点二:方差
考点梳理
例4
下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数和方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择____.
185
3.6
180
3.6
乙
甲
丙
丁
平均数(cm)
方差(cm )
180
185
7.4
8.1
甲
考点梳理
考点三:分析数据做决策
例1
生物工作者为了估计小山上山雀的数量,先捕了20只做上标记后放还,一星期后,又捕捉了40只山雀,发现带标记的有2只,由此估计小山上的山雀有____只.
400
考点梳理
例2
甲校和乙校九年级学生各有300名.为了解这两个学校九年级学生的英语单词掌握情况,进行了抽样调查,过程如下:
①收集数据.从两个学校九年级中各随机抽取10名学生,进行英语单词测试.
成绩如下:(百分制,单位:分)
甲校:92 100 86 89 73 98 54 95 98 85
乙校:100 100 94 83 74 86 75 100 73 75
②根据数据,填写下表:
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
考点梳理
例2
(1)若成绩90分以上为优秀估计乙校九年级学生英语单词掌握优秀的人数.
300×40%=120
解:样本容量为10的样本中,优秀的人数为4,可得样本中的优秀率为40%,据此推断总体中优秀率为40%.
因此乙校九年级学生英语单词掌握优秀的人数为120.
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
考点梳理
例2
(2)你认为那个学校的九年级学生英语单词掌握得比较好?说明你的理由.(至少从两个不同的角度说明推断的合理性).
解:乙校的九年级学生英语单词掌握得比较好.
理由:①乙校的九年级学生英语单词测试中,平均分高于甲校;②乙校的九年级学生在英语单词测试中,中位数较高,说明乙校英语单词测试成绩分数高的学生较多.
87
90.5
86
中位数/分
平均数/分
众数/分
方差/分
甲校
179.4
121.6
学校
乙校
84.5
98
100
刻意练习
练1
某公司 33 名职工的月工资(以元为单位)如下:
(1)求该公司职工月工资的平均数、中位数、众数.(精确到个位)
职工 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 5500 5000 3500 3000 2500 2000 1500
解析:(1)平均数
(元)
把这 33 个数据按照从小到大的顺序可得中位数为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了 20 次,所以众数为 1500.
刻意练习
练1
(2)假设副董事长的工资从 5000 元提升到 20000 元,董事长的工资从 5500 元提升到 30000 元,那么新的平均数、中位数、众数又是什么?(精确到个位)
(2)新的平均数
(元)
把这 33 个数据按照从小到大的顺序可得新的中位数仍为 1500.
这 33 个数据中出现次数最多的数据是 1500,出现了20 次,
所以新的众数仍为 1500.
