第22章 四边形(单元复习课件)-八年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 第22章 四边形(单元复习课件)-八年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-03 09:53:25 | ||
图片预览









文档简介
(共38张PPT)
单元复习课件
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第22章 四边形
多边形
注意:
1.多边形的内角和随着边数的增加而增加;
2.多边形的外角和为一个定值,与边数无关;
多边形的概念 凸多边形和凹多边形的定义 多边形内角和 多边形的外角和
平面内由不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.
对于一个多边形画出它任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形,否则叫做凹多边形.
360
名 称 定 义 性 质 判 定 面
积
平 行 四 边 形 两组对边 分别平行 的四边形 叫做平行 四边形. ①对边平行; ②对边相等; ③对角相等; ④对角线互相平分; ⑤是中心对称图形. ①两组对边分别平行的四边形; ②两组对边分别相等的四边形; ③一组对边平行且相等的四边形; ④两组对角分别相等的四边形; ⑤对角线互相平分的四边形. S=ah
平行四边形
(1)平行四边形两组对边分别_____________.
平行
平行且相等
相等
平分
平行四边形
两组对边分别_____的四边形是平行四边形.
(2)平行四边形的对角_____________.
(3)平行四边形的对角线互相_____________.
(4)平行四边形是中心对称图形,对称中心是___________________.
两条对角线的交点
2.平行四边形的性质
1.平行四边形的定义
(1)两组对边分别 的四边形是平行四边形.
(2)两组对边分别 的四边形是平行四边形.
(3)一组对边 的四边形是平行四边形.
(4)两组对角分别 的四边形是平行四边形.
(5)两条对角线 的四边形是平行四边形.
相等
平行
平行且相等
相等
互相平分
3.平行四边形的判定
平行四边形
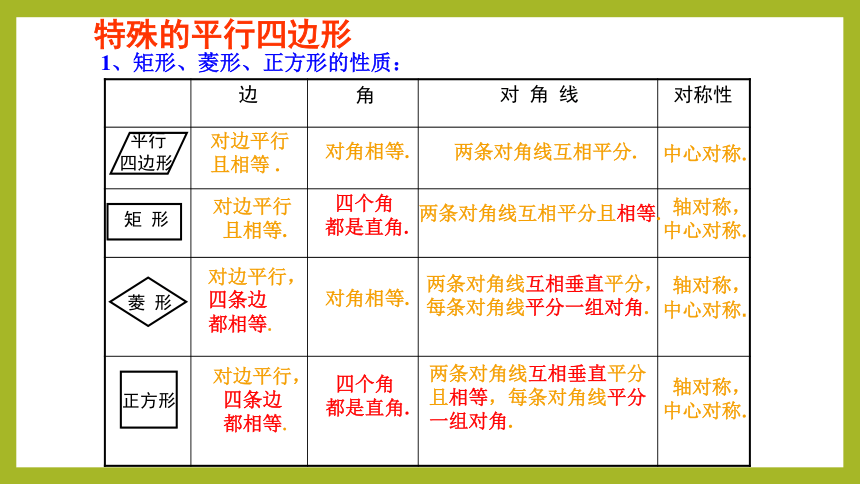
1、矩形、菱形、正方形的性质:
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角.
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等 .
对边平行
且相等.
对边平行,
四条边
都相等.
角
对角相等.
四个角
都是直角.
对角相等.
四个角
都是直角.
对 角 线
两条对角线互相平分.
两条对角线互相平分且相等.
两条对角线互相垂直平分,
每条对角线平分一组对角.
对称性
中心对称.
轴对称,
中心对称.
轴对称,
中心对称.
轴对称,
中心对称.
对边平行,
四条边
都相等.
特殊的平行四边形
四边形
四边形
平行四边形
矩 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
特殊的平行四边形
对角线相等
对角线互相垂直
菱形
三个内角都为90°
四条边都相等
一组对边平行而另一组对边不平行的四边形叫做梯形(trapezium).在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高(如图 22 -46(1)).
如图 22 - 46(2)(3),有一个角是直角的梯形叫做直角梯形(right-angled trapezium);两腰相等的梯形叫做等腰梯形(isoscelestrapezium),它们都是特殊的梯形.
梯形
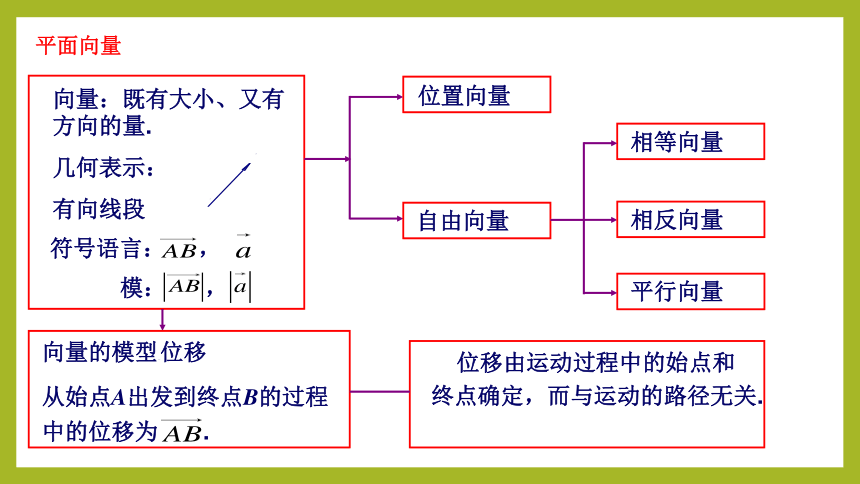
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
平面向量的加减
B
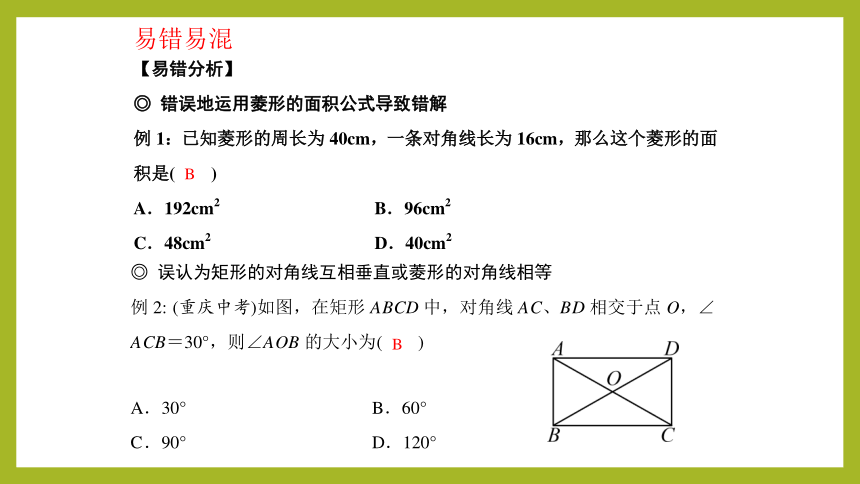
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
1.一个多边形的内角和是540°,这个多边形是( ____ )
A.五边形
B.六边形
C.七边形
D.八边形
【解析】解:设多边形的边数是n,则
(n-2) 180°=540°,
解得n=5,
∴这个多边形是五边形,
故选:A.
A
2.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
3.如图,已知四边形ABCD是平行四边形,那么添加下列条件能判定四边形ABCD是正方形的是( ____ )
A.AB=AD且AC⊥BD
B.AC⊥BD且AC和BD互相平分
C.∠BAD=∠ABC且AC=BD
D.AC=BD且AB=AD
【解析】解:A、AB=AD且AC⊥BD,是菱形,不符合题意;
B、对角线互直垂直且互相平分,是菱形,不符合题意;
C、∠BAD=∠ABC且AC=BD不能判断四边形ABCD是正方形,不符合题意;
D
D、AC=BD且AB=AD四边相等,是正方形,符合题意;
故选:D.
4.已知梯形的四条边长分别是4、5、7、8,则中位线长可以为( ____ )
A.4.5 B.5.5 C.6 D.6.5
【解析】解:如图,过D作DE∥AB,∴BE=AD,AB=DE,
∵梯形的四条边长分别是4、5、7、8,
当梯形的两底长分别为4和8,腰分别为5和7,
即DE=5,BE=4,
C
∴CE=4,
∵4+5>7,∴DE,CE,CD能构成三角形,
∴中位线长= (4+8)=6,
当梯形的两底长分别为5和8,腰分别为4和7,DE,CE,CD不能构成三角形,其他情况也是一样,
综上所述,中位线长可以为6,故选:C.
5.如果O是正方形ABCD对角线AC、BD的交点,那么向量 、 、 、 是( ____ )
A.相等向量 B.相反向量
C.平行向量 D.模相等的向量.
【解析】解:∵O是正方形ABCD对角线AC、BD的交点,
∴OA=OC=OB=OD,
∴| |=| |=| |=| |,
D
∵ 、 、 、 的方向不同,
∴ 、 、 、 是模相等的量,
故选:D.
6.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC′D′,如果∠DAD′=30°,那么菱形ABC′D′与正方形ABCD的面积之比是( ____ )
A. B. C. D.1
A
【解析】解:过D'作D'M⊥AB于M,如图所示:则∠D'MA=90°,
∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,∴∠D'AM=90°-30°=60°,∴∠AD'M=30°,
∴AM= AD',D'M= AM= AD',
∵四边形ABC′D′是菱形,∴AB=AD'=AD,菱形ABCD的面积=AB×D'M= AB2,
∴菱形ABC′D′与正方形ABCD的面积之比= = ,故选:A.
7.如图,菱形ABCD的对角线的长分别为12和15,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,那么阴影部分的面积是 ____ .
【解析】解:设AP与EF相交于O点.∵四边形ABCD为菱形,
45
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD,
∴PE∥AF,PF∥AE.
∴四边形AEFP是平行四边形.
∴阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
∴菱形ABCD的面积= AC BD=90,
∴图中阴影部分的面积为90÷2=45.
故答案为:45.
8.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
9.如图,在等腰梯形ABCD中,AB∥CD,对角线AC⊥BC,∠B=60°,BC=6cm,则梯形ABCD的周长为 ____ .
【解析】解:∵在等腰梯形ABCD中,AB∥CD,
∴AD=BC=6,
∵AC⊥BC,∠B=60°,
∴∠BAC=30°,∠DAB=∠B=60°,
∴AB=2BC=12,∠DAC=30°,
∵AB∥CD,
∴∠DCA=∠BAC=30°,
30
∴∠DAC=∠DCA,
∴AD=CD=6,
∴等腰梯形的周长为:AB+BC+CD+AD=12+6+6+6=30.
故答案为:30.
10.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
11.如图,在 ABCD中,AE⊥BC、AF⊥CD,垂足分别为E、F,若∠B=50°,则∠FAE的度数是 _____ .
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵∠B=50°,
∴∠C=180°-∠B=130°,
∵AE⊥BC、AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠FAE=360°-∠AEC-∠AFC-∠C=50°,
故答案为:50°.
50°
12.一个多边形的内角和是2880°,则这个多边形是 ____ 边形.
【解析】解:设这个多边形是n边形,根据题意,得
(n-2)×180°=2880°,
∴n=18.
故答案为:18.
18
13.我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为 和4,那么它的最大的内角为 _____ 度.
【解析】解:如图所示:
在平行四边形ABCD中,AB⊥AC,AB=2 ,BC=4时,∠BAD最大;
由勾股定理得:AC= =2 ,
∴AC=AB,
∴∠B=45°,
135
∴∠BAD=180°-∠B=135°.
故答案为:135.
14.如图,已知平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AC交AD边于点E,若△EDC的周长为15厘米,则平行四边形ABCD的周长为 ____ 厘米.
【解析】解:∵四边形ABCD是平行四边形,
∴O点为AC中点.
∵OE⊥AC,
∴AE=CE.
∴△EDC的周长=CD+CE+DE=CD+AE+DE=CD+AD=15.
∴平行四边形ABCD周长为2×15=30.
30
故答案为:30.
15.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,
∴AF= BC.
75
又∵DE=AF,
∴DE= BC= BD,
∴ = ,
∴sin∠1= ,
∴∠1=30°,
∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
16.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
17.如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 ____ .
【解析】解:∵点E,F分别是AD,AC的中点,
∴EF是△ACD的中位线,
∴ ,
∴CD=6,
∵∠BAC=90°,AD是△ABC的中线,
∴AD=CD=6.
故答案为:6.
6
18.如图,已知在△ABC中,AB=AC,点O是△ABC内任意一点,点D、G、E、F分别是AB,AC,OB,OC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)若∠A=2∠BDE,求证:四边形DEFG是矩形.
【解析】证明:(1)∵点D、G、E、F分别是AB,AC,OB,OC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,DG= BC,
同理:EF∥BC,EF= BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)∵点D、E、F、G分别是AB、AC、OB、OC的中点,
∴DG是△ABC的中位线,EF是△OBC的中位线,
∴DG∥BC,DG= BC,EF∥BC,EF= BC,
∴∠ADG=∠ABC,∠AGD=∠ACB,DG∥EF,DG=EF,
∴四边形DEGF是平行四边形,
∵AB=AC,∴∠ABC=∠ACB,
∴∠ADG=∠AGD,
∵∠ADG+∠AGD+∠A=180°,即2∠ADG+∠A=180°,
∴∠ADG+ ∠A=90°,
∵∠A=2∠BDE,∴∠BDE= ∠A,
∴∠ADG+∠BDE=90°,
∴∠EDG=180°-∠ADG-∠BDE=180°-90°=90°,
∴四边形DEFG是矩形.
解:由题意得:∠BDE=45o,
∴△BDE是等腰直角三角形.
过点A作AG⊥BC于点G.
可得四边形AGED为矩形(有三个角是直角的四边形是矩形).
∴AD=GE=2.
可得△ABG≌△DCE.
∴BG=CE=3.
∴BE=5.
45°
45°
2
8
┌
┌
G
2
3
3
F
E
D
C
B
A
19.已知:如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,将等腰梯形ABCD沿着折痕EF翻折,使点B与点D重合,折痕EF交边BC于E,边AB于F.若AD=2,BC=8.
求:BE的长.
20.已知:如图,正方形ABCD的边长为a,将正方形ABCD沿着折痕AE翻折,使点D落在对角线AC上点F处,联结EF,折痕AE交边CD于点E.求: FC的长.
∵AE平分∠DAC,
∴∠FAE=∠DAE.
又∵EF⊥AC,
∵四边形ABCD是正方形,
∠DCB=∠D=90°,
∴DE=FE.
又∵∠FCD=45°,
∴∠FEC=45°,
∴∠FCD=∠FEC,
∴EF=FC,
∴DE=FE=FC.
又∵EF2+FC2=EC2,
设FC=x,
∴EC= .
答:FC的长是 .
解:
A
B
C
D
E
F
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
∵△EBC,△FAC都是等边三角形,
∴AC=CF,BC=EC,
∠BCE=∠ACF= 60 .
∴∠1=∠2.
∴△ABC≌△FEC.
∴AB=FE.
∵△DBA是等边三角形,
∴AB=AD.
∴DA=FE.
同理 DE=AF,
∴四边形AFED是平行四边形
(两组对边分别相等的四边形是平行四边形).
证明:
(2)当△ABC满足什么条件时,平行四边形AFED是矩形?
满足什么条件的平行四边形是矩形?
有一个内角是直角的平行四边形是矩形.
找哪一个角是直角?
∠DAF=90 .又因为∠3=∠4=60 ,所以∠BAC=150 .
当∠BAC=150 时
∵∠3=∠4=60 ,
∴∠DAF=360 -150 -60 -60 =90 .
∴平行四边形AFED是矩形.
解:
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
满足什么条件的平行四边形是菱形?
有一组邻边相等的平行四边形是菱形.
(2)当△ABC满足什么条件时,平行四边形AFED是矩形?
找哪一组相等的邻边?
AF=AD,因而△ABC是等腰三角形,则AB=AC.
(3)当△ABC满足应什么条件时,平行四边形AFED是菱形?
当△ABC是等腰三角形,且AB=AC时,
∵AB=AD,AC=AF.
∴AF=AD .
又∵四边形AFED是平行四边形,
∴平行四边形AFED是菱形.
当AB=AC时,四边形AFED一定是菱形吗?
当△ABC是等腰三角形,且AB=AC、 ∠BAC≠60 时,
∵∠BAC ≠ 60 ,∠DAB=60 ,FAC=60 ,
∴∠DAB+∠BAC+∠CAF ≠180 ,
即点D、点A、点F不在同一直线上.
∴存在四边形AFED.
∵AB=AD,AC=AF.
∴AF=AD .
又∵四边形AFED是平行四边形,
∴平行四边形AFED是菱形.
解:
∴AE∥FC(平行四边形的对边平行).
∴∠1=∠2,
∵EF垂直平分AC,
∴AO=CO, ∠3=∠4=90°.
∵在△AOE和△COF中,
∴ △ AOE≌ △ COF(A.S.A).∴EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形). 又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).
∵四边形ABCD是平行四边形,
证明:
1
2
3
4
22.已知:如图,EF是□ABCD的对角线AC的垂直平分线,EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.
单元复习课件
2023-2024学年八年级下册数学同步精品课堂(沪教版)
第22章 四边形
多边形
注意:
1.多边形的内角和随着边数的增加而增加;
2.多边形的外角和为一个定值,与边数无关;
多边形的概念 凸多边形和凹多边形的定义 多边形内角和 多边形的外角和
平面内由不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.
对于一个多边形画出它任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形,否则叫做凹多边形.
360
名 称 定 义 性 质 判 定 面
积
平 行 四 边 形 两组对边 分别平行 的四边形 叫做平行 四边形. ①对边平行; ②对边相等; ③对角相等; ④对角线互相平分; ⑤是中心对称图形. ①两组对边分别平行的四边形; ②两组对边分别相等的四边形; ③一组对边平行且相等的四边形; ④两组对角分别相等的四边形; ⑤对角线互相平分的四边形. S=ah
平行四边形
(1)平行四边形两组对边分别_____________.
平行
平行且相等
相等
平分
平行四边形
两组对边分别_____的四边形是平行四边形.
(2)平行四边形的对角_____________.
(3)平行四边形的对角线互相_____________.
(4)平行四边形是中心对称图形,对称中心是___________________.
两条对角线的交点
2.平行四边形的性质
1.平行四边形的定义
(1)两组对边分别 的四边形是平行四边形.
(2)两组对边分别 的四边形是平行四边形.
(3)一组对边 的四边形是平行四边形.
(4)两组对角分别 的四边形是平行四边形.
(5)两条对角线 的四边形是平行四边形.
相等
平行
平行且相等
相等
互相平分
3.平行四边形的判定
平行四边形
1、矩形、菱形、正方形的性质:
两条对角线互相垂直平分
且相等,每条对角线平分
一组对角.
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等 .
对边平行
且相等.
对边平行,
四条边
都相等.
角
对角相等.
四个角
都是直角.
对角相等.
四个角
都是直角.
对 角 线
两条对角线互相平分.
两条对角线互相平分且相等.
两条对角线互相垂直平分,
每条对角线平分一组对角.
对称性
中心对称.
轴对称,
中心对称.
轴对称,
中心对称.
轴对称,
中心对称.
对边平行,
四条边
都相等.
特殊的平行四边形
四边形
四边形
平行四边形
矩 形
一角为90°
正方形
两组对边分别平行
一角为直角且一组邻边相等
一组邻边相等
一组邻边相等
一角为90°
特殊的平行四边形
对角线相等
对角线互相垂直
菱形
三个内角都为90°
四条边都相等
一组对边平行而另一组对边不平行的四边形叫做梯形(trapezium).在梯形中,平行的两边叫做梯形的底(通常把较短的底叫做上底,较长的底叫做下底);不平行的两边叫做梯形的腰;两底之间的距离叫做梯形的高(如图 22 -46(1)).
如图 22 - 46(2)(3),有一个角是直角的梯形叫做直角梯形(right-angled trapezium);两腰相等的梯形叫做等腰梯形(isoscelestrapezium),它们都是特殊的梯形.
梯形
向量:既有大小、又有方向的量.
几何表示:
有向线段
A
B
符号语言: ,
模: ,
位置向量
自由向量
相等向量
相反向量
平行向量
向量的模型——位移
从始点A出发到终点B的过程中的位移为 .
位移由运动过程中的始点和终点确定,而与运动的路径无关.
平面向量
一、向量加法的运算(作图)法则:
二、向量减法的运算(作图)法则:
1、三角形法则,(起点和终点重合)
2、多边形形法则(首尾依次相连接)
1、三角形法则(共起点,尾相连)
3、平行四边形法则(共起点,做平行四边形)
2、平行四边形法则(共起点,做平行四边形)
以共起点为起点的对角线向量,就是a,b的和向量;
与被减向量共终点的对角线向量,就是a,b的差向量。
平面向量的加减
B
易错易混
B
C
(3,2)或(-3,2)或(5,-2)
1.一个多边形的内角和是540°,这个多边形是( ____ )
A.五边形
B.六边形
C.七边形
D.八边形
【解析】解:设多边形的边数是n,则
(n-2) 180°=540°,
解得n=5,
∴这个多边形是五边形,
故选:A.
A
2.下列等式中不正确的是( ____ )
A.
B.-(- )=
C.( + )+ = +( + )
D. +(- )= -
【解析】解:A、 ,符合题意;
B、-(- )= ,不符合题意;
C、( + )+ = +( + ),不符合题意;
A
D、 +(- )= - ,不符合题意.
故选:A.
3.如图,已知四边形ABCD是平行四边形,那么添加下列条件能判定四边形ABCD是正方形的是( ____ )
A.AB=AD且AC⊥BD
B.AC⊥BD且AC和BD互相平分
C.∠BAD=∠ABC且AC=BD
D.AC=BD且AB=AD
【解析】解:A、AB=AD且AC⊥BD,是菱形,不符合题意;
B、对角线互直垂直且互相平分,是菱形,不符合题意;
C、∠BAD=∠ABC且AC=BD不能判断四边形ABCD是正方形,不符合题意;
D
D、AC=BD且AB=AD四边相等,是正方形,符合题意;
故选:D.
4.已知梯形的四条边长分别是4、5、7、8,则中位线长可以为( ____ )
A.4.5 B.5.5 C.6 D.6.5
【解析】解:如图,过D作DE∥AB,∴BE=AD,AB=DE,
∵梯形的四条边长分别是4、5、7、8,
当梯形的两底长分别为4和8,腰分别为5和7,
即DE=5,BE=4,
C
∴CE=4,
∵4+5>7,∴DE,CE,CD能构成三角形,
∴中位线长= (4+8)=6,
当梯形的两底长分别为5和8,腰分别为4和7,DE,CE,CD不能构成三角形,其他情况也是一样,
综上所述,中位线长可以为6,故选:C.
5.如果O是正方形ABCD对角线AC、BD的交点,那么向量 、 、 、 是( ____ )
A.相等向量 B.相反向量
C.平行向量 D.模相等的向量.
【解析】解:∵O是正方形ABCD对角线AC、BD的交点,
∴OA=OC=OB=OD,
∴| |=| |=| |=| |,
D
∵ 、 、 、 的方向不同,
∴ 、 、 、 是模相等的量,
故选:D.
6.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC′D′,如果∠DAD′=30°,那么菱形ABC′D′与正方形ABCD的面积之比是( ____ )
A. B. C. D.1
A
【解析】解:过D'作D'M⊥AB于M,如图所示:则∠D'MA=90°,
∵四边形ABCD是正方形,∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,∴∠D'AM=90°-30°=60°,∴∠AD'M=30°,
∴AM= AD',D'M= AM= AD',
∵四边形ABC′D′是菱形,∴AB=AD'=AD,菱形ABCD的面积=AB×D'M= AB2,
∴菱形ABC′D′与正方形ABCD的面积之比= = ,故选:A.
7.如图,菱形ABCD的对角线的长分别为12和15,P是对角线AC上任一点(点P不与点A、C重合)且PE∥BC交AB于E,PF∥CD交AD于F,那么阴影部分的面积是 ____ .
【解析】解:设AP与EF相交于O点.∵四边形ABCD为菱形,
45
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD,
∴PE∥AF,PF∥AE.
∴四边形AEFP是平行四边形.
∴阴影部分的面积等于△ABC的面积.
∵△ABC的面积等于菱形ABCD的面积的一半,
∴菱形ABCD的面积= AC BD=90,
∴图中阴影部分的面积为90÷2=45.
故答案为:45.
8.已知菱形的周长为40,一条对角线长为12,则这个菱形的面积是 ____ .
【解析】解:因为周长是40,所以边长是10.
如图所示:AB=10,AC=12.
根据菱形的性质,AC⊥BD,AO=6,
∴BO=8,BD=16.
∴面积S= AC×BD=12×16× =96.
故答案为96.
96
9.如图,在等腰梯形ABCD中,AB∥CD,对角线AC⊥BC,∠B=60°,BC=6cm,则梯形ABCD的周长为 ____ .
【解析】解:∵在等腰梯形ABCD中,AB∥CD,
∴AD=BC=6,
∵AC⊥BC,∠B=60°,
∴∠BAC=30°,∠DAB=∠B=60°,
∴AB=2BC=12,∠DAC=30°,
∵AB∥CD,
∴∠DCA=∠BAC=30°,
30
∴∠DAC=∠DCA,
∴AD=CD=6,
∴等腰梯形的周长为:AB+BC+CD+AD=12+6+6+6=30.
故答案为:30.
10.如图,已知在△ABC中,点D是边AC的中点,设 ,用向量 、 表示向量 = .
【解析】解:∵点D是边AC的中点,
∴ ,
又∵ ,
∴ =- ,
故答案为:- .
11.如图,在 ABCD中,AE⊥BC、AF⊥CD,垂足分别为E、F,若∠B=50°,则∠FAE的度数是 _____ .
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵∠B=50°,
∴∠C=180°-∠B=130°,
∵AE⊥BC、AF⊥CD,
∴∠AEC=∠AFC=90°,
∴∠FAE=360°-∠AEC-∠AFC-∠C=50°,
故答案为:50°.
50°
12.一个多边形的内角和是2880°,则这个多边形是 ____ 边形.
【解析】解:设这个多边形是n边形,根据题意,得
(n-2)×180°=2880°,
∴n=18.
故答案为:18.
18
13.我们把对角线与一边垂直的平行四边形叫做“优美平行四边形”.如果一个“优美平行四边形”的一组邻边长为 和4,那么它的最大的内角为 _____ 度.
【解析】解:如图所示:
在平行四边形ABCD中,AB⊥AC,AB=2 ,BC=4时,∠BAD最大;
由勾股定理得:AC= =2 ,
∴AC=AB,
∴∠B=45°,
135
∴∠BAD=180°-∠B=135°.
故答案为:135.
14.如图,已知平行四边形ABCD的对角线AC、BD相交于点O,OE⊥AC交AD边于点E,若△EDC的周长为15厘米,则平行四边形ABCD的周长为 ____ 厘米.
【解析】解:∵四边形ABCD是平行四边形,
∴O点为AC中点.
∵OE⊥AC,
∴AE=CE.
∴△EDC的周长=CD+CE+DE=CD+AE+DE=CD+AD=15.
∴平行四边形ABCD周长为2×15=30.
30
故答案为:30.
15.如图,梯形ABCD中,AD∥BC,∠BAC=90°,AB=AC,对角线AC与BD相交于点O,且BD=BC,那么∠AOB= ____ 度.
【解析】解:如图,作AF⊥BC于F,DE⊥BC于E,
在Rt△ABC中,
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴BC= AB,AF= AB,
∴AF= BC.
75
又∵DE=AF,
∴DE= BC= BD,
∴ = ,
∴sin∠1= ,
∴∠1=30°,
∴∠BOC=180°-30°-45°=105°,
∴∠AOB=180°-∠BOC=180°-105°=75°,
故答案为:75.
16.如图,在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,如果AB=2,EF=3,那么CD= ____ .
【解析】解:在梯形ABCD中,AB∥CD,点E、F分别是AD、BC的中点,
∴EF是梯形ABCD的中位线,
∴EF= (AB+CD),
∴CD=2EF-AB=6-2=4.
故答案为:4.
4
17.如图,在Rt△ABC中,∠BAC=90°,AD是△ABC的中线,点E,F分别是AD,AC的中点,连接EF,若EF=3,则AD的长为 ____ .
【解析】解:∵点E,F分别是AD,AC的中点,
∴EF是△ACD的中位线,
∴ ,
∴CD=6,
∵∠BAC=90°,AD是△ABC的中线,
∴AD=CD=6.
故答案为:6.
6
18.如图,已知在△ABC中,AB=AC,点O是△ABC内任意一点,点D、G、E、F分别是AB,AC,OB,OC的中点.
(1)求证:四边形DEFG是平行四边形;
(2)若∠A=2∠BDE,求证:四边形DEFG是矩形.
【解析】证明:(1)∵点D、G、E、F分别是AB,AC,OB,OC的中点,
∴DG是△ABC的中位线,
∴DG∥BC,DG= BC,
同理:EF∥BC,EF= BC,
∴DG∥EF,DG=EF,
∴四边形DEFG是平行四边形;
(2)∵点D、E、F、G分别是AB、AC、OB、OC的中点,
∴DG是△ABC的中位线,EF是△OBC的中位线,
∴DG∥BC,DG= BC,EF∥BC,EF= BC,
∴∠ADG=∠ABC,∠AGD=∠ACB,DG∥EF,DG=EF,
∴四边形DEGF是平行四边形,
∵AB=AC,∴∠ABC=∠ACB,
∴∠ADG=∠AGD,
∵∠ADG+∠AGD+∠A=180°,即2∠ADG+∠A=180°,
∴∠ADG+ ∠A=90°,
∵∠A=2∠BDE,∴∠BDE= ∠A,
∴∠ADG+∠BDE=90°,
∴∠EDG=180°-∠ADG-∠BDE=180°-90°=90°,
∴四边形DEFG是矩形.
解:由题意得:∠BDE=45o,
∴△BDE是等腰直角三角形.
过点A作AG⊥BC于点G.
可得四边形AGED为矩形(有三个角是直角的四边形是矩形).
∴AD=GE=2.
可得△ABG≌△DCE.
∴BG=CE=3.
∴BE=5.
45°
45°
2
8
┌
┌
G
2
3
3
F
E
D
C
B
A
19.已知:如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,将等腰梯形ABCD沿着折痕EF翻折,使点B与点D重合,折痕EF交边BC于E,边AB于F.若AD=2,BC=8.
求:BE的长.
20.已知:如图,正方形ABCD的边长为a,将正方形ABCD沿着折痕AE翻折,使点D落在对角线AC上点F处,联结EF,折痕AE交边CD于点E.求: FC的长.
∵AE平分∠DAC,
∴∠FAE=∠DAE.
又∵EF⊥AC,
∵四边形ABCD是正方形,
∠DCB=∠D=90°,
∴DE=FE.
又∵∠FCD=45°,
∴∠FEC=45°,
∴∠FCD=∠FEC,
∴EF=FC,
∴DE=FE=FC.
又∵EF2+FC2=EC2,
设FC=x,
∴EC= .
答:FC的长是 .
解:
A
B
C
D
E
F
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
∵△EBC,△FAC都是等边三角形,
∴AC=CF,BC=EC,
∠BCE=∠ACF= 60 .
∴∠1=∠2.
∴△ABC≌△FEC.
∴AB=FE.
∵△DBA是等边三角形,
∴AB=AD.
∴DA=FE.
同理 DE=AF,
∴四边形AFED是平行四边形
(两组对边分别相等的四边形是平行四边形).
证明:
(2)当△ABC满足什么条件时,平行四边形AFED是矩形?
满足什么条件的平行四边形是矩形?
有一个内角是直角的平行四边形是矩形.
找哪一个角是直角?
∠DAF=90 .又因为∠3=∠4=60 ,所以∠BAC=150 .
当∠BAC=150 时
∵∠3=∠4=60 ,
∴∠DAF=360 -150 -60 -60 =90 .
∴平行四边形AFED是矩形.
解:
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
21.已知:如图,以△ABC的三边为边在BC边的同侧作等边三角形△DBA,△EBC,△FAC.
(1)求证:四边形AFED是平行四边形.
满足什么条件的平行四边形是菱形?
有一组邻边相等的平行四边形是菱形.
(2)当△ABC满足什么条件时,平行四边形AFED是矩形?
找哪一组相等的邻边?
AF=AD,因而△ABC是等腰三角形,则AB=AC.
(3)当△ABC满足应什么条件时,平行四边形AFED是菱形?
当△ABC是等腰三角形,且AB=AC时,
∵AB=AD,AC=AF.
∴AF=AD .
又∵四边形AFED是平行四边形,
∴平行四边形AFED是菱形.
当AB=AC时,四边形AFED一定是菱形吗?
当△ABC是等腰三角形,且AB=AC、 ∠BAC≠60 时,
∵∠BAC ≠ 60 ,∠DAB=60 ,FAC=60 ,
∴∠DAB+∠BAC+∠CAF ≠180 ,
即点D、点A、点F不在同一直线上.
∴存在四边形AFED.
∵AB=AD,AC=AF.
∴AF=AD .
又∵四边形AFED是平行四边形,
∴平行四边形AFED是菱形.
解:
∴AE∥FC(平行四边形的对边平行).
∴∠1=∠2,
∵EF垂直平分AC,
∴AO=CO, ∠3=∠4=90°.
∵在△AOE和△COF中,
∴ △ AOE≌ △ COF(A.S.A).∴EO=FO.
∴四边形AFCE是平行四边形(对角线互相平分的四边形是平行四边形). 又∵EF⊥AC,
∴四边形AECF是菱形(对角线互相垂直的平行四边形是菱形).
∵四边形ABCD是平行四边形,
证明:
1
2
3
4
22.已知:如图,EF是□ABCD的对角线AC的垂直平分线,EF与边AD、BC分别交于点E、F.
求证:四边形AFCE是菱形.
