专题八:统计与概率复习课件(共31张PPT)六年级数学下学期期末核心考点集训(人教版)
文档属性
| 名称 | 专题八:统计与概率复习课件(共31张PPT)六年级数学下学期期末核心考点集训(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
专题08:统计与概率
期末专项考点复习
人教版·六年级下册
2023-2024学年
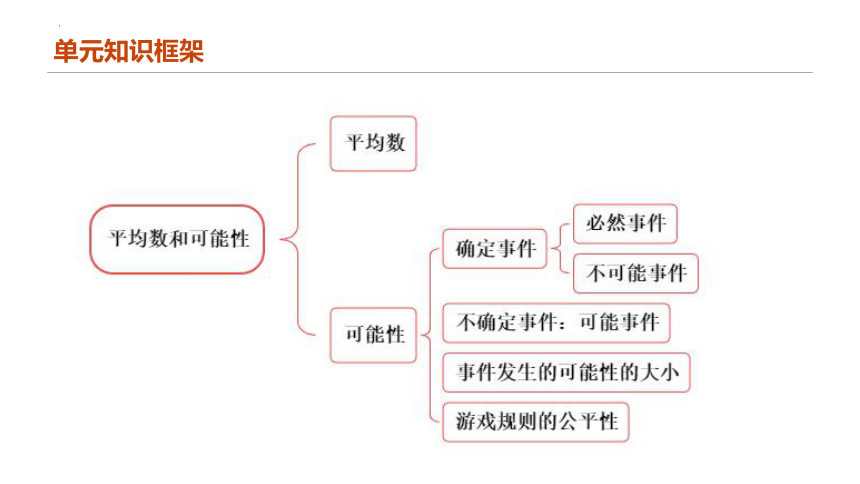
单元知识框架
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
中位数
众数
单元知识框架
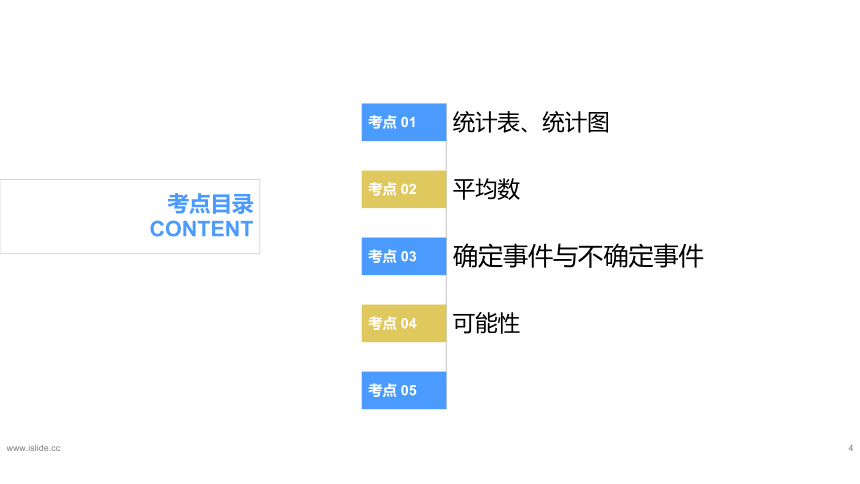
www.islide.cc考点目录CONTENT统计表、统计图平均数确定事件与不确定事件可能性考点01考点02考点03考点04考点05统计表、统计图
/01
知识梳理
(一)统计表
1.意义
把搜集到的资料进行数据整理后制成表格,用来分析情况,反映问题的这种表格叫做统计表。
2.分类
单式统计表:只有一个统计项目的统计表。
复式统计表:为了便于分析和比较,有时需要把几个有联系的统计表合编成一个统计表,含有两个或两个以上统计项目的统计表叫做复式统计表。
百分数统计表:不仅能表明统计项目的具体数量,而且可以表明比较某个量相当于标准量的百分比的统计表。
3.统计表的组成
包括表格内和表格外两部分。表格外部分包括总标题、单位说明、制表日期;
表格内部分包括表头、横栏目、纵栏目和数据四个方面。
4.制作步骤:收集数据,整理数据,设计草表,正式制表。
知识梳理
(二)统计图
1.意义
用点、线、面等来表示相关联的量之间的数量关系的图形叫做统计图。
用统计图表示有关数量之间的关系更为直接、具体、形象,使人耳目一新,印象深刻。
2.条形统计图
分类:单式条形统计图,复式条形统计图。
特点:用直条的长短表示数量的多少。
作用:从图中能直观地看出数量的多少,便于比较。
知识梳理
(二)统计图
3.折线统计图
分类:单式折线统计图,复式折线统计图。
特点:用不同位置的点表示数量的多少,并用折线的上升和下降来表示数量的增减变化情况。
作用:不仅能看清数量的多少,还能反映数量的增减变化情况。
4.扇形统计图
特点:以一个圆的面积表示物体的总数量,以相应的扇形面积表示各有关部分占总数量的百分数。
典型例题
【例1】根据统计图请制作一幅合适的统计表。
【解析】要制作一张合适的统计表,应按以下步骤:①整理数据; ②确定纵、横栏目的栏数; ③根据纸张大小制作表格;④填写数据;⑤写出总标题、说明和制表日期。
【解答】如下表
典型例题
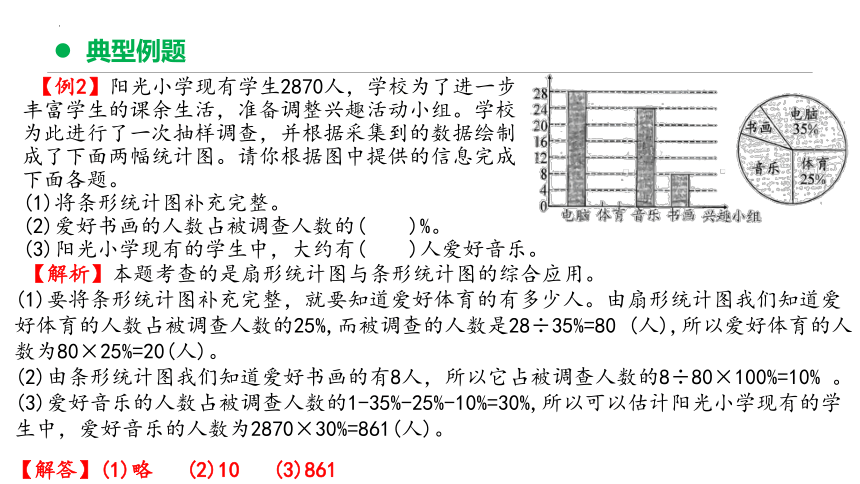
【例2】阳光小学现有学生2870人,学校为了进一步
丰富学生的课余生活,准备调整兴趣活动小组。学校
为此进行了一次抽样调查,并根据采集到的数据绘制
成了下面两幅统计图。请你根据图中提供的信息完成
下面各题。
(1)将条形统计图补充完整。
(2)爱好书画的人数占被调查人数的( )%。
(3)阳光小学现有的学生中,大约有( )人爱好音乐。
【解析】本题考查的是扇形统计图与条形统计图的综合应用。
(1)要将条形统计图补充完整,就要知道爱好体育的有多少人。由扇形统计图我们知道爱好体育的人数占被调查人数的25%,而被调查的人数是28÷35%=80 (人),所以爱好体育的人数为80×25%=20(人)。
(2)由条形统计图我们知道爱好书画的有8人,所以它占被调查人数的8÷80×100%=10% 。
(3)爱好音乐的人数占被调查人数的1-35%-25%-10%=30%,所以可以估计阳光小学现有的学生中,爱好音乐的人数为2870×30%=861(人)。
【解答】(1)略 (2)10 (3)861
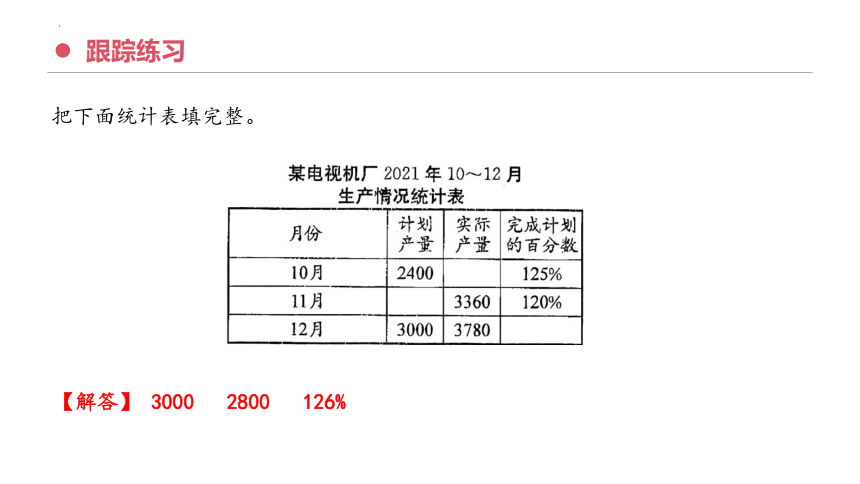
跟踪练习
把下面统计表填完整。
【解答】 3000 2800 126%
跟踪练习
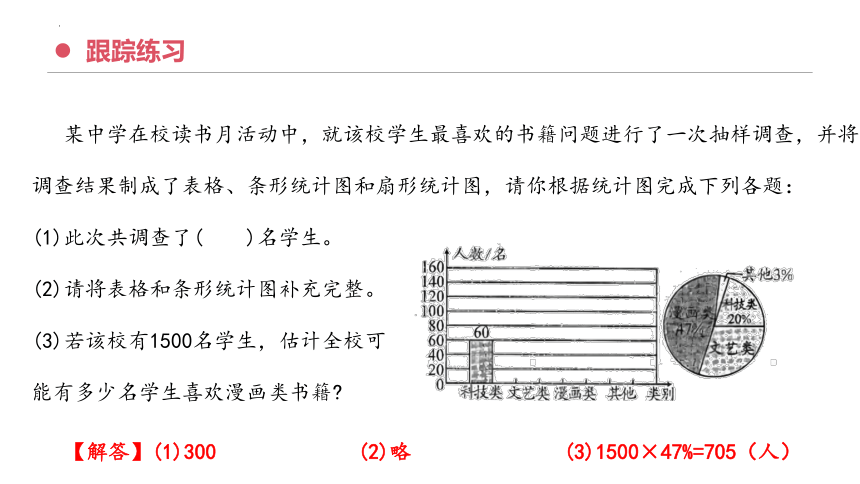
【解答】(1)300 (2)略 (3)1500×47%=705(人)
某中学在校读书月活动中,就该校学生最喜欢的书籍问题进行了一次抽样调查,并将调查结果制成了表格、条形统计图和扇形统计图,请你根据统计图完成下列各题:
(1)此次共调查了( )名学生。
(2)请将表格和条形统计图补充完整。
(3)若该校有1500名学生,估计全校可
能有多少名学生喜欢漫画类书籍
平均数
/02
知识梳理
1.定义
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。
平均数是表示数据集中程度的一个统计特征量。
2.求平均数的方法
根据平均教的意义,求平均数需要用几个数的和除以这些数量的总份数(总个数)。
平均数=总数÷总份数
总数=平均数×总份数
总份数=总数÷平均数
典型例题
【例】某班有40人,期末数学考试有1人缺考,其他同学的平均成绩是87.5分,后来缺考的同学补考后班级的平均成绩提高到87.7分,这个同学的成绩比其他同学的平均成绩高多少分
【解析】本题主要考查平均数的意义以及平均数的求法。因为补考的同学把高出全班平均成绩的部分移补给了其他39人,所以将班级平均成绩从87.5分提高到87.7分,平均成绩提高了87.7-87.5=0.2(分),说明补考的同学共移补给其他同学0.2×39=7.8(分),再加上自己比平均成绩高出的0.2分,则这个同学的成绩比其他同学的平均成绩高7.8+0.2=8(分)。
【解答】(87.7-87.5)×39+(87.7-87.5)=8(分)
答:这个同学的成绩比其他同学的平均成绩高8分。
跟踪练习
小李参加语文、数学、英语三门科目的测试,语文和英语两科的平均成绩是90分;数学和英语两科的平均成绩是91分;语文和数学两科的平均成绩是95分。小李三门科目的平均成绩是多少分
【解答】
(90×2+91×2+95×2)÷2÷ 3=92(分)
答:小李三门科目的平均成绩是92分。
确定事件与不确定事件
/03
知识梳理
典型例题
【例】判断。(对的打“√”,错的打“×”)。
(1)任意抛硬币4次,正面朝上的一定有2次。 ( )
(2)南京的夏天温度可能超过30℃。 ( )
(3)不遵守交通规则,发生事故的可能性很大。 ( )
【解析】(1)抛硬币,正面朝上和反面朝上的可能性是相等的,但发生次数不一定相等。
(2)南京夏天的气温是一个不确定现象,可能超过30℃,也可能不超过30℃。
(3)不遵守交通规则,容易导致交通事故,故发生事故的可能性很大。
【解答】(1)× (2)√ (3)√
跟踪练习
【解答】(1)一定 (2)不可能 (3)可能
在( )里填上“一定”“可能”或“不可能”。
(1)三角形的内角和( )是180°。
(2)妹妹的年龄( )比哥哥大。
(3)我们班连续三年运动会获总分第一名今年运动会我们班( )是第一名。
可能性
/04
知识梳理
可能性
1.可能性的大小
可能性的大小与事件的基本条件和发展过程等许多因素相关。
当条件对事件发生有利时,发生的可能性就大一些。
当条件对事件发生不利时,发生的可能性就小一些。
2.可能性大小的描述
一定>经常>可能>偶尔>不可能。
典型例题
【例】盒子里有10个红球、7个白球、3个黄球,球的大小和形状都相同,闭上眼睛从盒子中摸一个球,摸到什么颜色的球的可能性最大
【解析】根据在可能发生的事件中,如果出现该事件的情况较多,则该事件发生的可能性就大的原理,盒子中红球的个数多于白球和黄球的个数,即可作出判断。
【解答】答:摸到红球的可能性最大。
跟踪练习
【解答】A C
贝贝转动一个转盘20次,指针停在各区域的结果如下表。
贝贝最有可能转动的转盘是( ),
不可能转动的转盘是( )。
考点综合练习
【解答】1.条形统计图 折线统计图 扇形统计图 2.条形 折线 3. 24
4.(1)(1) (2) (2)113 77 36 (3)3 (4)17.7
一、填空
1.用统计图表示数量之间的关系比较直观。常用的统计图有三种,分别是( )、 ( )和( )。
2.要清楚地表示出小明每次考试的成绩,应该绘制( )统计图;若要表示出他成绩的变化趋势,绘制( )统计图比较好。
3.在一幅条形统计图中,如果用2cm长的直条表示16t,那么3cm长的直条表示( )t。
4.下面是六年级同学参加植树情况统计图。
(1)参加人数最多的是( )班,最少的是( )班。
(2)一共有( )人参加植树,其中男生有( )人,
女生有( )人。
(3)已知一共栽了339棵树,平均每人栽( )棵。
(4)六(3)班男生人数约占六年级植树总人数的( )%。
考点综合练习
学习时间分配统计图
5、上图是一个( )统计图,用直条的( ) 表示数量的( )。
6、条形统计图,可以看出数量的( ),还可以看出数量的( )情况。
条形
长短
多少
差异
多少
考点综合练习
在上面两组数据中,平均数、中位数和众数各是什么?
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
二、六(1)班同学身高、体重情况统计表
身高/m 1.40 1.43 1.46 1.49 1.52 1.55 1.58
人数 1 3 5 10 12 6 3
体重/kg 30 33 36 39 42 45 48
人数 2 4 5 12 10 4 3
考点综合练习
三、红星村农作物种植面积统计图。棉花种植了60公顷,农作物种植的总面积是多少公顷 其他粮食作物种植了多少公顷
农作物种植的总面积
解:60÷20%=300公顷
其他粮食作物种植
300×70%=210公顷
考点综合练习
四、据统计,2018年1月,某小学图书馆藏书中,故事书、科技书和连环画共20000本,请根据下面的统计图解决问题。
(1)故事书、科技书、连环画各有多少本
故:20000×30%=6000本
科:20000×45%=9000本
连:20000×25%=5000本
(2)故事书比科技书少多少本 连环画比科技书少多少本
(3)连环画是故事书的百分之几
9000-6000=3000本
9000-5000=4000本
5000÷6000≈83.3%
考点综合练习
五、某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”。游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元;若指 针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元。一天,前来玩游戏的人转动转盘80次,你认为该商人从中盈利的可能性大还是亏损的可能性大 为什么
【解答】
指向字母A的次数约为:80×50%=40(次)
指向字母B的次数约为:80×12.5%=10(次)
指向字母C 的次数约为:80×37.5%=30(次)
收入:40×2=80(元) 支出:10×3+30×1=60(元)
80>60,所以商人盈利的可能性大
乘风破浪会有时
直挂云帆济沧海
专题08:统计与概率
期末专项考点复习
人教版·六年级下册
2023-2024学年
单元知识框架
统计
数据的收集和整理
统计表
统计图
单式统计表
复式统计表
条形统计图(单式和复式)
折线统计图(单式和复式)
扇形统计图
统计量
平均数
中位数
众数
单元知识框架
www.islide.cc考点目录CONTENT统计表、统计图平均数确定事件与不确定事件可能性考点01考点02考点03考点04考点05统计表、统计图
/01
知识梳理
(一)统计表
1.意义
把搜集到的资料进行数据整理后制成表格,用来分析情况,反映问题的这种表格叫做统计表。
2.分类
单式统计表:只有一个统计项目的统计表。
复式统计表:为了便于分析和比较,有时需要把几个有联系的统计表合编成一个统计表,含有两个或两个以上统计项目的统计表叫做复式统计表。
百分数统计表:不仅能表明统计项目的具体数量,而且可以表明比较某个量相当于标准量的百分比的统计表。
3.统计表的组成
包括表格内和表格外两部分。表格外部分包括总标题、单位说明、制表日期;
表格内部分包括表头、横栏目、纵栏目和数据四个方面。
4.制作步骤:收集数据,整理数据,设计草表,正式制表。
知识梳理
(二)统计图
1.意义
用点、线、面等来表示相关联的量之间的数量关系的图形叫做统计图。
用统计图表示有关数量之间的关系更为直接、具体、形象,使人耳目一新,印象深刻。
2.条形统计图
分类:单式条形统计图,复式条形统计图。
特点:用直条的长短表示数量的多少。
作用:从图中能直观地看出数量的多少,便于比较。
知识梳理
(二)统计图
3.折线统计图
分类:单式折线统计图,复式折线统计图。
特点:用不同位置的点表示数量的多少,并用折线的上升和下降来表示数量的增减变化情况。
作用:不仅能看清数量的多少,还能反映数量的增减变化情况。
4.扇形统计图
特点:以一个圆的面积表示物体的总数量,以相应的扇形面积表示各有关部分占总数量的百分数。
典型例题
【例1】根据统计图请制作一幅合适的统计表。
【解析】要制作一张合适的统计表,应按以下步骤:①整理数据; ②确定纵、横栏目的栏数; ③根据纸张大小制作表格;④填写数据;⑤写出总标题、说明和制表日期。
【解答】如下表
典型例题
【例2】阳光小学现有学生2870人,学校为了进一步
丰富学生的课余生活,准备调整兴趣活动小组。学校
为此进行了一次抽样调查,并根据采集到的数据绘制
成了下面两幅统计图。请你根据图中提供的信息完成
下面各题。
(1)将条形统计图补充完整。
(2)爱好书画的人数占被调查人数的( )%。
(3)阳光小学现有的学生中,大约有( )人爱好音乐。
【解析】本题考查的是扇形统计图与条形统计图的综合应用。
(1)要将条形统计图补充完整,就要知道爱好体育的有多少人。由扇形统计图我们知道爱好体育的人数占被调查人数的25%,而被调查的人数是28÷35%=80 (人),所以爱好体育的人数为80×25%=20(人)。
(2)由条形统计图我们知道爱好书画的有8人,所以它占被调查人数的8÷80×100%=10% 。
(3)爱好音乐的人数占被调查人数的1-35%-25%-10%=30%,所以可以估计阳光小学现有的学生中,爱好音乐的人数为2870×30%=861(人)。
【解答】(1)略 (2)10 (3)861
跟踪练习
把下面统计表填完整。
【解答】 3000 2800 126%
跟踪练习
【解答】(1)300 (2)略 (3)1500×47%=705(人)
某中学在校读书月活动中,就该校学生最喜欢的书籍问题进行了一次抽样调查,并将调查结果制成了表格、条形统计图和扇形统计图,请你根据统计图完成下列各题:
(1)此次共调查了( )名学生。
(2)请将表格和条形统计图补充完整。
(3)若该校有1500名学生,估计全校可
能有多少名学生喜欢漫画类书籍
平均数
/02
知识梳理
1.定义
一组数据的和除以这组数据的个数所得的商叫做这组数据的平均数。
平均数是表示数据集中程度的一个统计特征量。
2.求平均数的方法
根据平均教的意义,求平均数需要用几个数的和除以这些数量的总份数(总个数)。
平均数=总数÷总份数
总数=平均数×总份数
总份数=总数÷平均数
典型例题
【例】某班有40人,期末数学考试有1人缺考,其他同学的平均成绩是87.5分,后来缺考的同学补考后班级的平均成绩提高到87.7分,这个同学的成绩比其他同学的平均成绩高多少分
【解析】本题主要考查平均数的意义以及平均数的求法。因为补考的同学把高出全班平均成绩的部分移补给了其他39人,所以将班级平均成绩从87.5分提高到87.7分,平均成绩提高了87.7-87.5=0.2(分),说明补考的同学共移补给其他同学0.2×39=7.8(分),再加上自己比平均成绩高出的0.2分,则这个同学的成绩比其他同学的平均成绩高7.8+0.2=8(分)。
【解答】(87.7-87.5)×39+(87.7-87.5)=8(分)
答:这个同学的成绩比其他同学的平均成绩高8分。
跟踪练习
小李参加语文、数学、英语三门科目的测试,语文和英语两科的平均成绩是90分;数学和英语两科的平均成绩是91分;语文和数学两科的平均成绩是95分。小李三门科目的平均成绩是多少分
【解答】
(90×2+91×2+95×2)÷2÷ 3=92(分)
答:小李三门科目的平均成绩是92分。
确定事件与不确定事件
/03
知识梳理
典型例题
【例】判断。(对的打“√”,错的打“×”)。
(1)任意抛硬币4次,正面朝上的一定有2次。 ( )
(2)南京的夏天温度可能超过30℃。 ( )
(3)不遵守交通规则,发生事故的可能性很大。 ( )
【解析】(1)抛硬币,正面朝上和反面朝上的可能性是相等的,但发生次数不一定相等。
(2)南京夏天的气温是一个不确定现象,可能超过30℃,也可能不超过30℃。
(3)不遵守交通规则,容易导致交通事故,故发生事故的可能性很大。
【解答】(1)× (2)√ (3)√
跟踪练习
【解答】(1)一定 (2)不可能 (3)可能
在( )里填上“一定”“可能”或“不可能”。
(1)三角形的内角和( )是180°。
(2)妹妹的年龄( )比哥哥大。
(3)我们班连续三年运动会获总分第一名今年运动会我们班( )是第一名。
可能性
/04
知识梳理
可能性
1.可能性的大小
可能性的大小与事件的基本条件和发展过程等许多因素相关。
当条件对事件发生有利时,发生的可能性就大一些。
当条件对事件发生不利时,发生的可能性就小一些。
2.可能性大小的描述
一定>经常>可能>偶尔>不可能。
典型例题
【例】盒子里有10个红球、7个白球、3个黄球,球的大小和形状都相同,闭上眼睛从盒子中摸一个球,摸到什么颜色的球的可能性最大
【解析】根据在可能发生的事件中,如果出现该事件的情况较多,则该事件发生的可能性就大的原理,盒子中红球的个数多于白球和黄球的个数,即可作出判断。
【解答】答:摸到红球的可能性最大。
跟踪练习
【解答】A C
贝贝转动一个转盘20次,指针停在各区域的结果如下表。
贝贝最有可能转动的转盘是( ),
不可能转动的转盘是( )。
考点综合练习
【解答】1.条形统计图 折线统计图 扇形统计图 2.条形 折线 3. 24
4.(1)(1) (2) (2)113 77 36 (3)3 (4)17.7
一、填空
1.用统计图表示数量之间的关系比较直观。常用的统计图有三种,分别是( )、 ( )和( )。
2.要清楚地表示出小明每次考试的成绩,应该绘制( )统计图;若要表示出他成绩的变化趋势,绘制( )统计图比较好。
3.在一幅条形统计图中,如果用2cm长的直条表示16t,那么3cm长的直条表示( )t。
4.下面是六年级同学参加植树情况统计图。
(1)参加人数最多的是( )班,最少的是( )班。
(2)一共有( )人参加植树,其中男生有( )人,
女生有( )人。
(3)已知一共栽了339棵树,平均每人栽( )棵。
(4)六(3)班男生人数约占六年级植树总人数的( )%。
考点综合练习
学习时间分配统计图
5、上图是一个( )统计图,用直条的( ) 表示数量的( )。
6、条形统计图,可以看出数量的( ),还可以看出数量的( )情况。
条形
长短
多少
差异
多少
考点综合练习
在上面两组数据中,平均数、中位数和众数各是什么?
身高:
平均数:(1.4+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3) ÷40
=60.17 ÷40
≈1.50(m)
体重:
平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3) ÷40
=1584 ÷40
=39.6(kg)
中位数:就是第20、21名之间的身高。所以中位数是1.52。
众数:1.52。
中位数:就是第20、21名之间的体重。所以中位数是39。
众数:39。
二、六(1)班同学身高、体重情况统计表
身高/m 1.40 1.43 1.46 1.49 1.52 1.55 1.58
人数 1 3 5 10 12 6 3
体重/kg 30 33 36 39 42 45 48
人数 2 4 5 12 10 4 3
考点综合练习
三、红星村农作物种植面积统计图。棉花种植了60公顷,农作物种植的总面积是多少公顷 其他粮食作物种植了多少公顷
农作物种植的总面积
解:60÷20%=300公顷
其他粮食作物种植
300×70%=210公顷
考点综合练习
四、据统计,2018年1月,某小学图书馆藏书中,故事书、科技书和连环画共20000本,请根据下面的统计图解决问题。
(1)故事书、科技书、连环画各有多少本
故:20000×30%=6000本
科:20000×45%=9000本
连:20000×25%=5000本
(2)故事书比科技书少多少本 连环画比科技书少多少本
(3)连环画是故事书的百分之几
9000-6000=3000本
9000-5000=4000本
5000÷6000≈83.3%
考点综合练习
五、某商人制成了一个如图所示的转盘游戏,取名为“开心大转盘”。游戏规定:参与者自由转动转盘,若指针指向字母“A”,则收费2元;若指 针指向字母“B”,则奖3元;若指针指向字母“C”,则奖1元。一天,前来玩游戏的人转动转盘80次,你认为该商人从中盈利的可能性大还是亏损的可能性大 为什么
【解答】
指向字母A的次数约为:80×50%=40(次)
指向字母B的次数约为:80×12.5%=10(次)
指向字母C 的次数约为:80×37.5%=30(次)
收入:40×2=80(元) 支出:10×3+30×1=60(元)
80>60,所以商人盈利的可能性大
乘风破浪会有时
直挂云帆济沧海
