2.1 气体实验定律Ⅰ 第二课时 课件(49张PPT)
文档属性
| 名称 | 2.1 气体实验定律Ⅰ 第二课时 课件(49张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-30 22:17:39 | ||
图片预览









文档简介
(共49张PPT)
第二章 气体、液体和固体
粤教版 选择性必修三
第一节 气体实验定律Ⅰ
——玻意耳定律的应用
Part 01
气体压强的计算方法
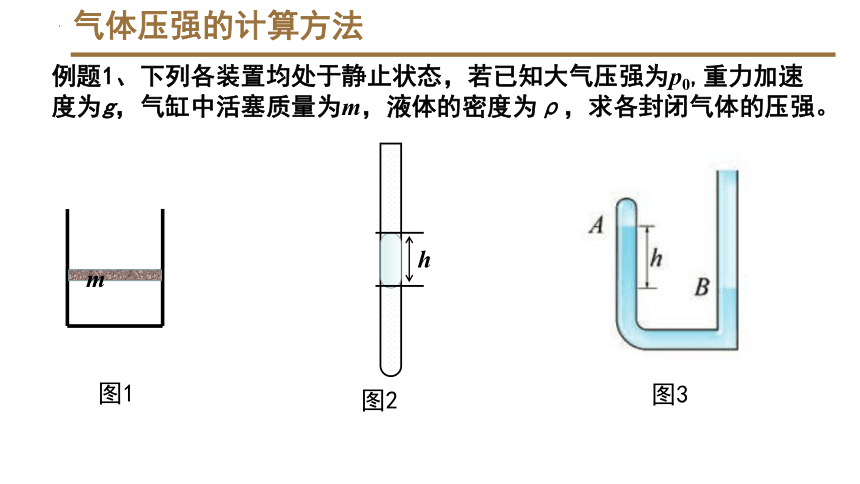
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
h
图1
图2
图3
m
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,气缸的横截面积为S,液体的密度为ρ,求各封闭气体的压强。
图1
mg
F0=p0S
F=pS
解:设气缸中气体的压强为p
根据活塞处于平衡状态,对活塞进行受力分析如图,列出平衡方程:
pS=p0S+mg
(1)力平衡法求气体压强
得:p=p0+mg/S
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图2
h
mg
F0=p0S
F=pS
列平衡方程:
pS=p0S+mg
设玻璃管的横截面积为S,封闭气体压强为p.
对液体:m=ρV ,V=Sh
p=p0+ρgh
h
p0
ph
p
同一液面两侧压强相等
(2)等压面法求压强
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图3
ph
pA
p1
p0
p2
对左边液面:pA+ph=p1
对右边液面:p0=p2
选择一合适的液面,如图所示
左右两边为同一液面深度p1=p2
联立方程:pA+ph=p0
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图3
ph
pA
p0
选择一合适的液面,如图所示
方程:pA+ph=p0
(2)等压面法求气体的压强
适用于在底部连通的容器中气体压强的计算
同种液体同一液面深度压强相等
气体压强的计算方法
封闭气体气体压强的计算方法总结
(1)求气缸中活塞封闭的气体压强:力平衡法
1.适用于玻璃直管中封闭的气体
2.适用于底部连通的容器中封闭的气体
(2)玻璃管中液柱封闭的气体压强:
等压面法
mg
F0=p0S
F1=p1S
h
p0
ph
p1
p0
ph
pA
p1S=p0S+mg
pA+ph=p0
特点:同种液体同一液面深度压强相等
p1=p0+ph
1.如图所示,活塞的质量为m,缸套的质量为m0,通过弹簧吊在天花板上,气缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强p为( )
A.p=p0+ B.p=p0+
C.p=p0- D.p=
C [以缸套为研究对象,根据受力平衡有pS+m0g=p0S,所以封闭气体的压强p=p0-,故应选C.]
C
课堂练习
课堂练习
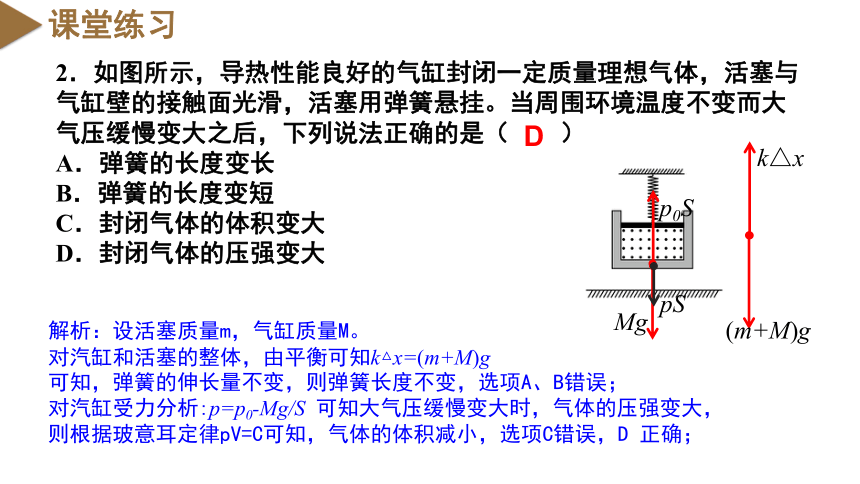
2.如图所示,导热性能良好的气缸封闭一定质量理想气体,活塞与气缸壁的接触面光滑,活塞用弹簧悬挂。当周围环境温度不变而大气压缓慢变大之后,下列说法正确的是( )
A.弹簧的长度变长
B.弹簧的长度变短
C.封闭气体的体积变大
D.封闭气体的压强变大
解析:设活塞质量m,气缸质量M。
对汽缸和活塞的整体,由平衡可知k△x=(m+M)g
可知,弹簧的伸长量不变,则弹簧长度不变,选项A、B错误;
对汽缸受力分析:p=p0-Mg/S 可知大气压缓慢变大时,气体的压强变大,则根据玻意耳定律pV=C可知,气体的体积减小,选项C错误,D 正确;
D
k△x
(m+M)g
p0S
Mg
pS
3、若已知大气压强为p0,在图中各装置均处于静止状态,图中液体密度均为ρ,求被封闭气体的压强.
课堂练习
课堂练习
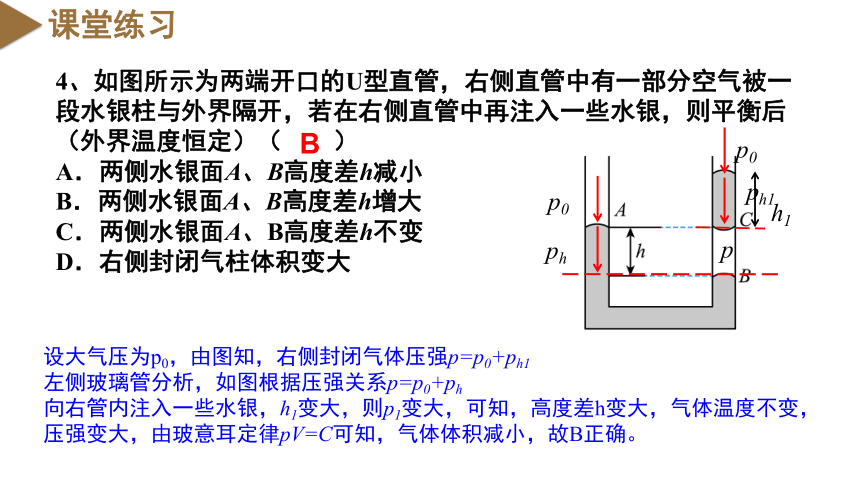
4、如图所示为两端开口的U型直管,右侧直管中有一部分空气被一段水银柱与外界隔开,若在右侧直管中再注入一些水银,则平衡后(外界温度恒定)( )
A.两侧水银面A、B高度差h减小
B.两侧水银面A、B高度差h增大
C.两侧水银面A、B高度差h不变
D.右侧封闭气柱体积变大
设大气压为p0,由图知,右侧封闭气体压强p=p0+ph1
左侧玻璃管分析,如图根据压强关系p=p0+ph
向右管内注入一些水银,h1变大,则p1变大,可知,高度差h变大,气体温度不变,压强变大,由玻意耳定律pV=C可知,气体体积减小,故B正确。
B
h1
p
p0
ph1
p0
ph
Part 02
玻意耳定律的应用
——气缸类问题
例题.导热性良好的圆柱形气缸内,面积为S=6×10-4m2,质量为m=2kg的活塞封闭了一定质量的理想气体,处在温度恒定,大气压强为p0=1.0×105Pa的环境中。如图甲,气缸开口向上放置时,活塞距缸底的高度为h1。重力加速度g取10 m/s2。不计活塞与气缸内壁的摩擦。先将气缸缓慢倒转,重新达到平衡后(如图乙),求活塞距缸底的距离h2。
图甲
图乙
考向1 气缸类问题
例题.导热性良好的圆柱形气缸内,面积为S=6×10-4m2,质量为m=2kg的活塞封闭了一定质量的理想气体,处在温度恒定,大气压强为p0=1.0×105Pa的环境中。如图甲,气缸开口向上放置时,活塞静止时距缸底的高度为h1=10cm。重力加速度g取10 m/s2。不计活塞与气缸内壁的摩擦。先将气缸缓慢倒转,重新达到平衡后(如图乙),求活塞距缸底的距离h2。
气体初态:活塞静止列平衡方程 p1S=p0S+mg
mg
F0=p0S
F1=p1S
气体末态:活塞重新平衡有 p0S=p2S+mg
解得:h2=20cm
mg
F2=p2S
F0=p0S
由玻意耳定律得:p1V1=p2V2
解:
V1=Sh1 ;
得:p1=p0+mg/S
得 p2=p0-mg/S
V2=Sh2 ;
图甲
图乙
考向1 气缸类问题
2、(2023年湖北卷高考真题)如图所示,竖直放置在水平桌面上的左右两汽缸粗细均匀,内壁光滑,横截面积分别为S、2S,由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质量的理想气体封闭左侧汽缸底部与活塞用轻质细弹簧相连。初始时,两汽缸内封闭气柱的高度均为H ,弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降1/2 H,左侧活塞上升2/3 H。已知大气压强为p0,重力加速度大小为g,汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内。求:
(1)最终汽缸内气体的压强。
(2)弹簧的劲度系数和添加的沙子质量。
考向1 气缸类问题
(1)对左右气缸内所封的气体,初态压强
体积
末态体积
设末态压强,根据玻意耳定律可得 ,解得
(2)对右边活塞受力分析可知,解得
对左侧活塞受力分析可知,解得
2、左右两汽缸横截面积分别为S、2S,由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质量的理想气体封闭左侧汽缸底部与活塞用轻质细弹簧相连。初始时,两汽缸内封闭气柱的高度均为H ,弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降1/2 H,左侧活塞上升2/3 H。已知大气压强为p0,重力加速度大小为g,汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内。求:
(1)最终汽缸内气体的压强。(2)弹簧的劲度系数和添加的沙子质量。
总结 应用玻意耳定律解题思路:
1、明确研究对象(一定质量的气体)
2、确定气体初末状态参量
气体初态:p1、V1
气体末态:p2、V2
3、根据玻意耳定律列方程
p1V1=p2V2
Part 03
玻意耳定律的应用
——变质量问题
玻意耳定律实际应用(教材第22页例题)
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(1)保温瓶中的水越少,需要按压瓶盖的次数越多,才能将水从瓶中压出,请分析其原因
h
解:设瓶内压强为p,外界大气压强为p0
要使水压出则压强满足:p0+ρgh=p
水越少,h越大,压出水所需要的压强就越大
同时,保温瓶内水上方的空气体积越大,每次从气室中压入空气相对体积的比例就越少,故所需要的次数就越多
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(2)已知保温瓶中水的占比,估测出水所需要的按压次数,需用到什么实验定律?若满足该气体定律的适用条件,应怎样选择研究对象?
解:气室体积远小于瓶内水上方的空气体积,气体被压缩时瓶内温度变化很小,近似看作温度不变,所以需要用到玻意耳定律
玻意耳定律条件:质量不变、温度恒定
气室气体
瓶内原气体
+
=
瓶内总气体
瓶内气体质量增大不满足质量不变的条件
将压入瓶中的空气和瓶内原空气看成一个整体,为研究对象
玻意耳定律实际应用(教材第22页例题)
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(3)若保温瓶中只有半桶水时,希望压两次就能出水,则还需要满足什么条件?
如图,设保温瓶的体积为V1,瓶盖下方气室体积为V2,出水口到瓶内水平的高度为h,水密度ρ,大气压强p0
2次气室气体
瓶内气体
+
=
瓶内总气体
初态
末态
解:
初态:p=p0 , V =2V2+V1/2
初态:p =p0+ρgh , V =V1/2
据玻意耳定律得:pV=p V
解得:V1:V2=4p0:ρgh
玻意耳定律实际应用(教材第22页例题)
考向2 气体变质量问题
打进容器内的气体和容器内原有的气体
研究对象
打气
考向2 气体变质量问题——打气
一个足球的容积为V=2.5L。 用打气筒给这个足球打气,每打一次都把体积为V0=125mL、压强与大气压相同的气体打进足球内。如果在大气前足球就已经是球形并且里面的压强与大气压相同,打了n=20次后足球内部空气的压强是大气压的多少倍?(大气压为P0)
研究对象:打进容器内的气体和容器内原有的气体
考向2 气体变质量问题——打气
一个足球的容积为V=2.5L。 用打气筒给这个足球打气,每打一次都把体积为V0=125mL、压强与大气压相同的气体打进足球内。如果在大气前足球就已经是球形并且里面的压强与大气压相同,打了n=20次后足球内部空气的压强是大气压的多少倍?(大气压为P0)
将变质量问题变成定质量问题
具体处理如下:
将打进容器内的气体和容器内原有的气体为研究对象视为气体的初始状态,汇总后为气体的末状态,这样总气体质量前、后相同(质量保持不变)
解:由玻意耳定律:
P0(V+nV0)=PV
代入数据解得:P=2P0
是大气压的2倍
【练习】用打气筒将压强为1 atm的空气打进自行车胎内,如果打气筒容积ΔV=500 cm3,轮胎容积V=3 L,原来压强 p=1.5 atm.现要使轮胎内压强变为p′=4 atm,问用这个打气筒要打气多少次?(设打气过程中空气的温度不变).
考向2 气体变质量问题——打气
研究对象:打进容器内的气体和容器内原有的气体
【练习】用打气筒将压强为1 atm的空气打进自行车胎内,如果打气筒容积ΔV=500 cm3,轮胎容积V=3 L,原来压强 p=1.5 atm.现要使轮胎内压强变为p′=4 atm,问用这个打气筒要打气多少次?(设打气过程中空气的温度不变).
解:由玻意耳定律:
pV+np1ΔV=p′V
代入数据得:n=15(次)
考向2 气体变质量问题——打气
如果打气时每一次打入的空气质量、体积和压强不相同,则将若干部分(p1,V1,m1)、(p2,V2,m2)、…、(pn、Vn、mn),合并成(p,V,m)一部分,满足p1V1+p2V2+…+pnVn=pV
练习:容积V=20 L的钢瓶充满氧气后,压强p=30 atm,打开钢瓶阀门,让氧气分装到容积为V′=5 L的小瓶中去,小瓶子已抽成真空.分装完成后,每个小钢瓶的压强p′=2 atm.在分装过程中无漏气现象,且温度保持不变,那么最多可能装的瓶数是( )
A.4瓶 B.50瓶 C.56瓶 D.60瓶
C
考向2 气体变质量问题——打气
练习:容积V=20 L的钢瓶充满氧气后,压强p=30 atm,打开钢瓶阀门,让氧气分装到容积为V′=5 L的小瓶中去,小瓶子已抽成真空.分装完成后,每个小钢瓶的压强p′=2 atm.在分装过程中无漏气现象,且温度保持不变,那么最多可能装的瓶数是( )
A.4瓶 B.50瓶 C.56瓶 D.60瓶
C
分装气体(每部分压强相等)就是充气的逆过程,解决方法与充气相同。
解:由玻意耳定律:
PV=P/(V+nV/)
代入数据得:n=56(瓶)
考向2 气体变质量问题——打气
考向2 气体变质量问题——漏气
例题1:某个容器的容积是V1=10L,所装气体的压强是P1=2×106Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是P0=1.0×105Pa.
研究对象:容器内剩余气体和漏出的气体组成的整体
考向2 气体变质量问题——漏气
例题1:某个容器的容积是V1=10L,所装气体的压强是P1=2×106Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是P0=1.0×105Pa.
将变质量问题变成定质量问题
具体处理如下:
容器漏气过程中气体的质量不断发生变化,属于变质量问题。如果选容器内剩余气体和漏出的气体组成的整体为研究对象,便可使问题变成一定质量的气体的状态变化问题。
P1 V1
P2 V2
等温膨胀
解:P2 =P0=1.0×105Pa
由玻意耳定律:P1V1=P2V2
容器里剩下的气体是原来比值
解得:容器里剩下的气体是原来的5%
考向2 气体变质量问题
容器内剩余气体和漏出的气体
打进容器内的气体和容器内原有的气体
研究对象
漏气
打气
考向2 气体变质量问题——漏气
【练习】一位消防员在火灾现场发现一个容积为V0的废弃的氧气罐(视为容积不变),经检测,内部封闭气体压强为1.2P0,为了消除安全隐患,该消防员拟用下面处理方案:保持罐内气体温度不变,缓慢地放出一部分气体,使气体压强降为P0,求氧气罐内剩余气体的质量与原来总质量之比。
考向2 气体变质量问题——漏气
【练习】一位消防员在火灾现场发现一个容积为V0的废弃的氧气罐(视为容积不变),经检测,内部封闭气体压强为1.2P0,为了消除安全隐患,该消防员拟用下面处理方案:保持罐内气体温度不变,缓慢地放出一部分气体,使气体压强降为P0,求氧气罐内剩余气体的质量与原来总质量之比。
解:假设将放出的气体收集起来,并保持压强与氧气罐内相同,以全部气体为研究对象,由玻意耳定律得p1V0=p0V
考向2 气体变质量问题——漏气
【练习】 (2020高考全国)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为P;乙罐的容积为2V,罐中气体的压强为0.5P。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后
(1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
考向2 气体变质量问题——漏气
【练习】 (2020高考全国)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为P;乙罐的容积为2V,罐中气体的压强为0.5P。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后 (1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
(1)由玻意耳定律,PV+0.5P·2V=P/2V
(2)若调配后甲罐中的气体再被压缩到原来的压强P时,体积为V甲,由玻意耳定律 P′V=PV甲
设调配后甲罐中气体的质量与甲罐中原有气体的质量之比为
解得:
考向2 气体变质量问题——抽气
【例题】活塞式抽气机气缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B. C. D.
C
研究对象:每次抽气过程中抽出的气体和剩余气体
考向2 气体变质量问题——抽气
将变质量问题变成定质量问题
具体处理如下:
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量的问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可看作是等温膨胀过程。
?
【例题】活塞式抽气机气缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B. C. D.
C
考向2 气体变质量问题
容器内剩余气体和漏出的气体
打进容器内的气体和容器内原有的气体
研究对象
漏气
打气
抽气
每次抽气过程中抽出的气体和剩余气体
考向2 气体变质量问题——抽气
练习:恒温室内有容积为V=100L的储气钢瓶,钢瓶中装有压强为P0的理想气体,现使用两种方式抽取钢瓶中气体,第一种方式使用大抽气机,一次缓慢抽取V1=10L气体,第二种方式使用小抽气机,缓慢抽两次,每次抽取V2=5L气体. 求:(1)第一种方式抽气后钢瓶内气体的压强P1
(2)第二种方式抽气后钢瓶内气体的压强P2,并比较P1和P2大小关系.
考向2 气体变质量问题——抽气
练习:恒温室内有容积为V=100L的储气钢瓶,钢瓶中装有压强为P0的理想气体,现使用两种方式抽取钢瓶中气体,第一种方式使用大抽气机,一次缓慢抽取V1=10L气体,第二种方式使用小抽气机,缓慢抽两次,每次抽取V2=5L气体. 求:(1)第一种方式抽气后钢瓶内气体的压强P1
(2)第二种方式抽气后钢瓶内气体的压强P2,并比较P1和P2大小关系.
根据计算结果可得P1>P2
解析:(1)第一种方式为等温变化,初始体积为V=100L,压强为P0,末态体积V+V1=110L,压强为P1, 由玻意耳定律P0V=P1(V+V1) 解得
(2)第二种方式第一次抽取,末态压强为P2/,体积V+V2=105L, 由玻意耳定律可得P0V=P2/(V+V2 ) 解得
同理第二次抽取,由玻意耳定律可得P2/V=P2V2 解得
Part 04
玻意耳定律的应用
——液柱类问题
考向3 液柱类问题
1、一竖直放置的粗细均匀的 U形玻璃管中,两边分别灌有等高的水银,右管中封闭有一定质量的理想气体,如图所示。h1=15cm,h2=25cm,现从左管口缓慢倒入水银,恰好使右管中水银面上升6cm。已知大气压强P0 =76cmHg,环境温度不变,左管足够长。求:
(1) 此时右管封闭气体的压强; (2) 左管中需要倒入水银柱的长度。
考向3 液柱类问题
1、一竖直放置的粗细均匀的 U形玻璃管中,两边分别灌有等高的水银,右管中封闭有一定质量的理想气体,如图所示。h1=15cm,h2=25cm,现从左管口缓慢倒入水银,恰好使右管中水银面上升6cm。已知大气压强P0 =76cmHg,环境温度不变,左管足够长。求:
(1) 此时右管封闭气体的压强; (2) 左管中需要倒入水银柱的长度。
(1)设玻璃管的横截面积为S,对右管中的气体
初态为p1= p0=76cmHg,V1=25cm·S;
末态为V2=(25cm-6cm)·S=19 cm·S
由玻意耳定律有p1V1=p2V2,解得p2=100cmHg
(2)设倒入水银柱的高度为h,则左侧水银柱比右侧高h-12cm,
由平衡条件可得p0+h-12cm=p2,解得h=36cm
考向3 液柱类问题
2、如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长hl=25.0cm的空气柱,中间有一段长为h2=25.0 cm的水银柱,上部空气柱的长度h3=60.0cm。已知大气压强为P0=75.0 cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为h1’=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。
考向3 液柱类问题
2、如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长hl=25.0cm的空气柱,中间有一段长为h2=25.0 cm的水银柱,上部空气柱的长度h3=60.0cm。已知大气压强为P0=75.0 cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为h1’=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。
活塞未下推之前,液柱下端封闭气体的压强
液柱下端封闭气体,根据玻意耳定律可知 ,
其中,
联立解得
活塞下推后,管上部分气体的压强为
对管上部分气体,根据玻意耳定律,其中 ,
联立解得,管上部分气体的长度
活塞下推的距离为
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
(1)对A侧空气柱
状态1(如图1)
,
状态2(如图2)
,
由玻意耳定律得
解得
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
(2)对A侧空气柱状态3(如图3)
,
由玻意耳定律得
解得
注入的水银在管内的长度
第二章 气体、液体和固体
粤教版 选择性必修三
第一节 气体实验定律Ⅰ
——玻意耳定律的应用
Part 01
气体压强的计算方法
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
h
图1
图2
图3
m
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,气缸的横截面积为S,液体的密度为ρ,求各封闭气体的压强。
图1
mg
F0=p0S
F=pS
解:设气缸中气体的压强为p
根据活塞处于平衡状态,对活塞进行受力分析如图,列出平衡方程:
pS=p0S+mg
(1)力平衡法求气体压强
得:p=p0+mg/S
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图2
h
mg
F0=p0S
F=pS
列平衡方程:
pS=p0S+mg
设玻璃管的横截面积为S,封闭气体压强为p.
对液体:m=ρV ,V=Sh
p=p0+ρgh
h
p0
ph
p
同一液面两侧压强相等
(2)等压面法求压强
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图3
ph
pA
p1
p0
p2
对左边液面:pA+ph=p1
对右边液面:p0=p2
选择一合适的液面,如图所示
左右两边为同一液面深度p1=p2
联立方程:pA+ph=p0
气体压强的计算方法
例题1、下列各装置均处于静止状态,若已知大气压强为p0,重力加速度为g,气缸中活塞质量为m,液体的密度为ρ,求各封闭气体的压强。
图3
ph
pA
p0
选择一合适的液面,如图所示
方程:pA+ph=p0
(2)等压面法求气体的压强
适用于在底部连通的容器中气体压强的计算
同种液体同一液面深度压强相等
气体压强的计算方法
封闭气体气体压强的计算方法总结
(1)求气缸中活塞封闭的气体压强:力平衡法
1.适用于玻璃直管中封闭的气体
2.适用于底部连通的容器中封闭的气体
(2)玻璃管中液柱封闭的气体压强:
等压面法
mg
F0=p0S
F1=p1S
h
p0
ph
p1
p0
ph
pA
p1S=p0S+mg
pA+ph=p0
特点:同种液体同一液面深度压强相等
p1=p0+ph
1.如图所示,活塞的质量为m,缸套的质量为m0,通过弹簧吊在天花板上,气缸内封住一定质量的气体,缸套和活塞间无摩擦,活塞面积为S,大气压强为p0,则封闭气体的压强p为( )
A.p=p0+ B.p=p0+
C.p=p0- D.p=
C [以缸套为研究对象,根据受力平衡有pS+m0g=p0S,所以封闭气体的压强p=p0-,故应选C.]
C
课堂练习
课堂练习
2.如图所示,导热性能良好的气缸封闭一定质量理想气体,活塞与气缸壁的接触面光滑,活塞用弹簧悬挂。当周围环境温度不变而大气压缓慢变大之后,下列说法正确的是( )
A.弹簧的长度变长
B.弹簧的长度变短
C.封闭气体的体积变大
D.封闭气体的压强变大
解析:设活塞质量m,气缸质量M。
对汽缸和活塞的整体,由平衡可知k△x=(m+M)g
可知,弹簧的伸长量不变,则弹簧长度不变,选项A、B错误;
对汽缸受力分析:p=p0-Mg/S 可知大气压缓慢变大时,气体的压强变大,则根据玻意耳定律pV=C可知,气体的体积减小,选项C错误,D 正确;
D
k△x
(m+M)g
p0S
Mg
pS
3、若已知大气压强为p0,在图中各装置均处于静止状态,图中液体密度均为ρ,求被封闭气体的压强.
课堂练习
课堂练习
4、如图所示为两端开口的U型直管,右侧直管中有一部分空气被一段水银柱与外界隔开,若在右侧直管中再注入一些水银,则平衡后(外界温度恒定)( )
A.两侧水银面A、B高度差h减小
B.两侧水银面A、B高度差h增大
C.两侧水银面A、B高度差h不变
D.右侧封闭气柱体积变大
设大气压为p0,由图知,右侧封闭气体压强p=p0+ph1
左侧玻璃管分析,如图根据压强关系p=p0+ph
向右管内注入一些水银,h1变大,则p1变大,可知,高度差h变大,气体温度不变,压强变大,由玻意耳定律pV=C可知,气体体积减小,故B正确。
B
h1
p
p0
ph1
p0
ph
Part 02
玻意耳定律的应用
——气缸类问题
例题.导热性良好的圆柱形气缸内,面积为S=6×10-4m2,质量为m=2kg的活塞封闭了一定质量的理想气体,处在温度恒定,大气压强为p0=1.0×105Pa的环境中。如图甲,气缸开口向上放置时,活塞距缸底的高度为h1。重力加速度g取10 m/s2。不计活塞与气缸内壁的摩擦。先将气缸缓慢倒转,重新达到平衡后(如图乙),求活塞距缸底的距离h2。
图甲
图乙
考向1 气缸类问题
例题.导热性良好的圆柱形气缸内,面积为S=6×10-4m2,质量为m=2kg的活塞封闭了一定质量的理想气体,处在温度恒定,大气压强为p0=1.0×105Pa的环境中。如图甲,气缸开口向上放置时,活塞静止时距缸底的高度为h1=10cm。重力加速度g取10 m/s2。不计活塞与气缸内壁的摩擦。先将气缸缓慢倒转,重新达到平衡后(如图乙),求活塞距缸底的距离h2。
气体初态:活塞静止列平衡方程 p1S=p0S+mg
mg
F0=p0S
F1=p1S
气体末态:活塞重新平衡有 p0S=p2S+mg
解得:h2=20cm
mg
F2=p2S
F0=p0S
由玻意耳定律得:p1V1=p2V2
解:
V1=Sh1 ;
得:p1=p0+mg/S
得 p2=p0-mg/S
V2=Sh2 ;
图甲
图乙
考向1 气缸类问题
2、(2023年湖北卷高考真题)如图所示,竖直放置在水平桌面上的左右两汽缸粗细均匀,内壁光滑,横截面积分别为S、2S,由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质量的理想气体封闭左侧汽缸底部与活塞用轻质细弹簧相连。初始时,两汽缸内封闭气柱的高度均为H ,弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降1/2 H,左侧活塞上升2/3 H。已知大气压强为p0,重力加速度大小为g,汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内。求:
(1)最终汽缸内气体的压强。
(2)弹簧的劲度系数和添加的沙子质量。
考向1 气缸类问题
(1)对左右气缸内所封的气体,初态压强
体积
末态体积
设末态压强,根据玻意耳定律可得 ,解得
(2)对右边活塞受力分析可知,解得
对左侧活塞受力分析可知,解得
2、左右两汽缸横截面积分别为S、2S,由体积可忽略的细管在底部连通。两汽缸中各有一轻质活塞将一定质量的理想气体封闭左侧汽缸底部与活塞用轻质细弹簧相连。初始时,两汽缸内封闭气柱的高度均为H ,弹簧长度恰好为原长。现往右侧活塞上表面缓慢添加一定质量的沙子,直至右侧活塞下降1/2 H,左侧活塞上升2/3 H。已知大气压强为p0,重力加速度大小为g,汽缸足够长,汽缸内气体温度始终不变,弹簧始终在弹性限度内。求:
(1)最终汽缸内气体的压强。(2)弹簧的劲度系数和添加的沙子质量。
总结 应用玻意耳定律解题思路:
1、明确研究对象(一定质量的气体)
2、确定气体初末状态参量
气体初态:p1、V1
气体末态:p2、V2
3、根据玻意耳定律列方程
p1V1=p2V2
Part 03
玻意耳定律的应用
——变质量问题
玻意耳定律实际应用(教材第22页例题)
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(1)保温瓶中的水越少,需要按压瓶盖的次数越多,才能将水从瓶中压出,请分析其原因
h
解:设瓶内压强为p,外界大气压强为p0
要使水压出则压强满足:p0+ρgh=p
水越少,h越大,压出水所需要的压强就越大
同时,保温瓶内水上方的空气体积越大,每次从气室中压入空气相对体积的比例就越少,故所需要的次数就越多
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(2)已知保温瓶中水的占比,估测出水所需要的按压次数,需用到什么实验定律?若满足该气体定律的适用条件,应怎样选择研究对象?
解:气室体积远小于瓶内水上方的空气体积,气体被压缩时瓶内温度变化很小,近似看作温度不变,所以需要用到玻意耳定律
玻意耳定律条件:质量不变、温度恒定
气室气体
瓶内原气体
+
=
瓶内总气体
瓶内气体质量增大不满足质量不变的条件
将压入瓶中的空气和瓶内原空气看成一个整体,为研究对象
玻意耳定律实际应用(教材第22页例题)
例题:人们使用气压式保温瓶时只需要按压保温瓶顶端,即可将水从瓶中压出。如图所示是气压式保温瓶结构图,请分析下列问题。
(3)若保温瓶中只有半桶水时,希望压两次就能出水,则还需要满足什么条件?
如图,设保温瓶的体积为V1,瓶盖下方气室体积为V2,出水口到瓶内水平的高度为h,水密度ρ,大气压强p0
2次气室气体
瓶内气体
+
=
瓶内总气体
初态
末态
解:
初态:p=p0 , V =2V2+V1/2
初态:p =p0+ρgh , V =V1/2
据玻意耳定律得:pV=p V
解得:V1:V2=4p0:ρgh
玻意耳定律实际应用(教材第22页例题)
考向2 气体变质量问题
打进容器内的气体和容器内原有的气体
研究对象
打气
考向2 气体变质量问题——打气
一个足球的容积为V=2.5L。 用打气筒给这个足球打气,每打一次都把体积为V0=125mL、压强与大气压相同的气体打进足球内。如果在大气前足球就已经是球形并且里面的压强与大气压相同,打了n=20次后足球内部空气的压强是大气压的多少倍?(大气压为P0)
研究对象:打进容器内的气体和容器内原有的气体
考向2 气体变质量问题——打气
一个足球的容积为V=2.5L。 用打气筒给这个足球打气,每打一次都把体积为V0=125mL、压强与大气压相同的气体打进足球内。如果在大气前足球就已经是球形并且里面的压强与大气压相同,打了n=20次后足球内部空气的压强是大气压的多少倍?(大气压为P0)
将变质量问题变成定质量问题
具体处理如下:
将打进容器内的气体和容器内原有的气体为研究对象视为气体的初始状态,汇总后为气体的末状态,这样总气体质量前、后相同(质量保持不变)
解:由玻意耳定律:
P0(V+nV0)=PV
代入数据解得:P=2P0
是大气压的2倍
【练习】用打气筒将压强为1 atm的空气打进自行车胎内,如果打气筒容积ΔV=500 cm3,轮胎容积V=3 L,原来压强 p=1.5 atm.现要使轮胎内压强变为p′=4 atm,问用这个打气筒要打气多少次?(设打气过程中空气的温度不变).
考向2 气体变质量问题——打气
研究对象:打进容器内的气体和容器内原有的气体
【练习】用打气筒将压强为1 atm的空气打进自行车胎内,如果打气筒容积ΔV=500 cm3,轮胎容积V=3 L,原来压强 p=1.5 atm.现要使轮胎内压强变为p′=4 atm,问用这个打气筒要打气多少次?(设打气过程中空气的温度不变).
解:由玻意耳定律:
pV+np1ΔV=p′V
代入数据得:n=15(次)
考向2 气体变质量问题——打气
如果打气时每一次打入的空气质量、体积和压强不相同,则将若干部分(p1,V1,m1)、(p2,V2,m2)、…、(pn、Vn、mn),合并成(p,V,m)一部分,满足p1V1+p2V2+…+pnVn=pV
练习:容积V=20 L的钢瓶充满氧气后,压强p=30 atm,打开钢瓶阀门,让氧气分装到容积为V′=5 L的小瓶中去,小瓶子已抽成真空.分装完成后,每个小钢瓶的压强p′=2 atm.在分装过程中无漏气现象,且温度保持不变,那么最多可能装的瓶数是( )
A.4瓶 B.50瓶 C.56瓶 D.60瓶
C
考向2 气体变质量问题——打气
练习:容积V=20 L的钢瓶充满氧气后,压强p=30 atm,打开钢瓶阀门,让氧气分装到容积为V′=5 L的小瓶中去,小瓶子已抽成真空.分装完成后,每个小钢瓶的压强p′=2 atm.在分装过程中无漏气现象,且温度保持不变,那么最多可能装的瓶数是( )
A.4瓶 B.50瓶 C.56瓶 D.60瓶
C
分装气体(每部分压强相等)就是充气的逆过程,解决方法与充气相同。
解:由玻意耳定律:
PV=P/(V+nV/)
代入数据得:n=56(瓶)
考向2 气体变质量问题——打气
考向2 气体变质量问题——漏气
例题1:某个容器的容积是V1=10L,所装气体的压强是P1=2×106Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是P0=1.0×105Pa.
研究对象:容器内剩余气体和漏出的气体组成的整体
考向2 气体变质量问题——漏气
例题1:某个容器的容积是V1=10L,所装气体的压强是P1=2×106Pa。如果温度保持不变,把容器的开关打开以后,经过足够长时间,容器里剩下的气体是原来的百分之几?设大气压是P0=1.0×105Pa.
将变质量问题变成定质量问题
具体处理如下:
容器漏气过程中气体的质量不断发生变化,属于变质量问题。如果选容器内剩余气体和漏出的气体组成的整体为研究对象,便可使问题变成一定质量的气体的状态变化问题。
P1 V1
P2 V2
等温膨胀
解:P2 =P0=1.0×105Pa
由玻意耳定律:P1V1=P2V2
容器里剩下的气体是原来比值
解得:容器里剩下的气体是原来的5%
考向2 气体变质量问题
容器内剩余气体和漏出的气体
打进容器内的气体和容器内原有的气体
研究对象
漏气
打气
考向2 气体变质量问题——漏气
【练习】一位消防员在火灾现场发现一个容积为V0的废弃的氧气罐(视为容积不变),经检测,内部封闭气体压强为1.2P0,为了消除安全隐患,该消防员拟用下面处理方案:保持罐内气体温度不变,缓慢地放出一部分气体,使气体压强降为P0,求氧气罐内剩余气体的质量与原来总质量之比。
考向2 气体变质量问题——漏气
【练习】一位消防员在火灾现场发现一个容积为V0的废弃的氧气罐(视为容积不变),经检测,内部封闭气体压强为1.2P0,为了消除安全隐患,该消防员拟用下面处理方案:保持罐内气体温度不变,缓慢地放出一部分气体,使气体压强降为P0,求氧气罐内剩余气体的质量与原来总质量之比。
解:假设将放出的气体收集起来,并保持压强与氧气罐内相同,以全部气体为研究对象,由玻意耳定律得p1V0=p0V
考向2 气体变质量问题——漏气
【练习】 (2020高考全国)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为P;乙罐的容积为2V,罐中气体的压强为0.5P。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后
(1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
考向2 气体变质量问题——漏气
【练习】 (2020高考全国)甲、乙两个储气罐储存有同种气体(可视为理想气体)。甲罐的容积为V,罐中气体的压强为P;乙罐的容积为2V,罐中气体的压强为0.5P。现通过连接两罐的细管把甲罐中的部分气体调配到乙罐中去,两罐中气体温度相同且在调配过程中保持不变,调配后两罐中气体的压强相等。求调配后 (1)两罐中气体的压强;
(2)甲罐中气体的质量与甲罐中原有气体的质量之比。
(1)由玻意耳定律,PV+0.5P·2V=P/2V
(2)若调配后甲罐中的气体再被压缩到原来的压强P时,体积为V甲,由玻意耳定律 P′V=PV甲
设调配后甲罐中气体的质量与甲罐中原有气体的质量之比为
解得:
考向2 气体变质量问题——抽气
【例题】活塞式抽气机气缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B. C. D.
C
研究对象:每次抽气过程中抽出的气体和剩余气体
考向2 气体变质量问题——抽气
将变质量问题变成定质量问题
具体处理如下:
从容器内抽气的过程中,容器内的气体质量不断减小,这属于变质量的问题。分析时,将每次抽气过程中抽出的气体和剩余气体作为研究对象,质量不变,故抽气过程可看作是等温膨胀过程。
?
【例题】活塞式抽气机气缸容积为V,用它给容积为2V的容器抽气,抽气机抽动两次(抽气过程可视为等温变化),容器内剩余气体压强是原来的( )
A. B. C. D.
C
考向2 气体变质量问题
容器内剩余气体和漏出的气体
打进容器内的气体和容器内原有的气体
研究对象
漏气
打气
抽气
每次抽气过程中抽出的气体和剩余气体
考向2 气体变质量问题——抽气
练习:恒温室内有容积为V=100L的储气钢瓶,钢瓶中装有压强为P0的理想气体,现使用两种方式抽取钢瓶中气体,第一种方式使用大抽气机,一次缓慢抽取V1=10L气体,第二种方式使用小抽气机,缓慢抽两次,每次抽取V2=5L气体. 求:(1)第一种方式抽气后钢瓶内气体的压强P1
(2)第二种方式抽气后钢瓶内气体的压强P2,并比较P1和P2大小关系.
考向2 气体变质量问题——抽气
练习:恒温室内有容积为V=100L的储气钢瓶,钢瓶中装有压强为P0的理想气体,现使用两种方式抽取钢瓶中气体,第一种方式使用大抽气机,一次缓慢抽取V1=10L气体,第二种方式使用小抽气机,缓慢抽两次,每次抽取V2=5L气体. 求:(1)第一种方式抽气后钢瓶内气体的压强P1
(2)第二种方式抽气后钢瓶内气体的压强P2,并比较P1和P2大小关系.
根据计算结果可得P1>P2
解析:(1)第一种方式为等温变化,初始体积为V=100L,压强为P0,末态体积V+V1=110L,压强为P1, 由玻意耳定律P0V=P1(V+V1) 解得
(2)第二种方式第一次抽取,末态压强为P2/,体积V+V2=105L, 由玻意耳定律可得P0V=P2/(V+V2 ) 解得
同理第二次抽取,由玻意耳定律可得P2/V=P2V2 解得
Part 04
玻意耳定律的应用
——液柱类问题
考向3 液柱类问题
1、一竖直放置的粗细均匀的 U形玻璃管中,两边分别灌有等高的水银,右管中封闭有一定质量的理想气体,如图所示。h1=15cm,h2=25cm,现从左管口缓慢倒入水银,恰好使右管中水银面上升6cm。已知大气压强P0 =76cmHg,环境温度不变,左管足够长。求:
(1) 此时右管封闭气体的压强; (2) 左管中需要倒入水银柱的长度。
考向3 液柱类问题
1、一竖直放置的粗细均匀的 U形玻璃管中,两边分别灌有等高的水银,右管中封闭有一定质量的理想气体,如图所示。h1=15cm,h2=25cm,现从左管口缓慢倒入水银,恰好使右管中水银面上升6cm。已知大气压强P0 =76cmHg,环境温度不变,左管足够长。求:
(1) 此时右管封闭气体的压强; (2) 左管中需要倒入水银柱的长度。
(1)设玻璃管的横截面积为S,对右管中的气体
初态为p1= p0=76cmHg,V1=25cm·S;
末态为V2=(25cm-6cm)·S=19 cm·S
由玻意耳定律有p1V1=p2V2,解得p2=100cmHg
(2)设倒入水银柱的高度为h,则左侧水银柱比右侧高h-12cm,
由平衡条件可得p0+h-12cm=p2,解得h=36cm
考向3 液柱类问题
2、如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长hl=25.0cm的空气柱,中间有一段长为h2=25.0 cm的水银柱,上部空气柱的长度h3=60.0cm。已知大气压强为P0=75.0 cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为h1’=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。
考向3 液柱类问题
2、如图,一上端开口、下端封闭的细长玻璃管竖直放置。玻璃管的下部封有长hl=25.0cm的空气柱,中间有一段长为h2=25.0 cm的水银柱,上部空气柱的长度h3=60.0cm。已知大气压强为P0=75.0 cmHg。现将一活塞(图中未画出)从玻璃管开口处缓缓往下推,使管下部空气柱长度变为h1’=20.0cm。假设活塞下推过程中没有漏气,求活塞下推的距离。
活塞未下推之前,液柱下端封闭气体的压强
液柱下端封闭气体,根据玻意耳定律可知 ,
其中,
联立解得
活塞下推后,管上部分气体的压强为
对管上部分气体,根据玻意耳定律,其中 ,
联立解得,管上部分气体的长度
活塞下推的距离为
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
(1)对A侧空气柱
状态1(如图1)
,
状态2(如图2)
,
由玻意耳定律得
解得
考向3 液柱类问题
3、如图,一粗细均匀的U形管竖直放置,A侧上端封闭,B侧上端与大气相通,下端开口处开关K关闭;A侧空气柱的长度L=15.0cm,B侧水银面比A侧的高h=3.0cm。现将开关K打开,从U形管中放出部分水银,当两侧水银面的高度差为h1=10.0cm时将开关K关闭。已知大气压强p0=75.0cmHg。
(1)求放出部分水银后A侧空气柱的长度;
(2)此后再向B侧注入水银,使A、B两侧的水银面达到同一高度,
求注入的水银在管内的长度。
(2)对A侧空气柱状态3(如图3)
,
由玻意耳定律得
解得
注入的水银在管内的长度
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
