2.2 气体实验定律Ⅱ 课件(26张PPT)
文档属性
| 名称 | 2.2 气体实验定律Ⅱ 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 20.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第二章 气体、液体和固体
粤教版 选择性必修三
第一节 气体实验定律Ⅱ
知识回顾
一定质量的气体,其温度、体积和压强三个量之间存在某种关系。
探究气体等温变化的规律
探究三个量之间的变化关系?
控制变量法
探究气体等容变化的规律
探究气体等压变化的规律
—— 玻意耳定律
Part 01
探究气体等容变化的规律
(一)提出猜想
观察下列日常生活现象,猜想在等容变化中,气体的压强与温度可能存在着什么关系呢?
瓶吞鸡蛋
车辆在夏季容易爆胎
定性分析:
一定质量的某种气体,保持体积不变,当温度升高时,气体的压强增大;当温度降低时,气体的压强减小。
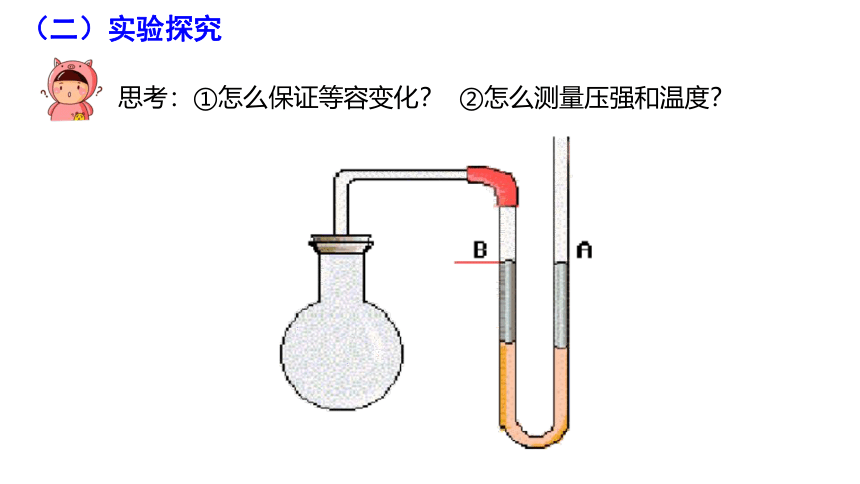
(二)实验探究
思考:①怎么保证等容变化? ②怎么测量压强和温度?
(二)实验探究
思考:①怎么保证等容变化? ②怎么测量压强和温度?
P1=P0
P2=P0-ρgh
P3=P0+ρgh
移动压强计右侧玻璃管使得左管上液面每次恢复到标记处
(三)实验结论
实验结论:气体体积一定时,各种气体的压强都随温度的升高均匀增大。
O
P
t/
A
B
℃
外推
P=Ct+P0
-273.15℃
A
B
T/K
P
O
P=CT
热力学温度T=t+273.15 K
简洁美
热力学温度(T),国际单位开尔文,简称开,符号K
压强P与热力学温度 T 成正比
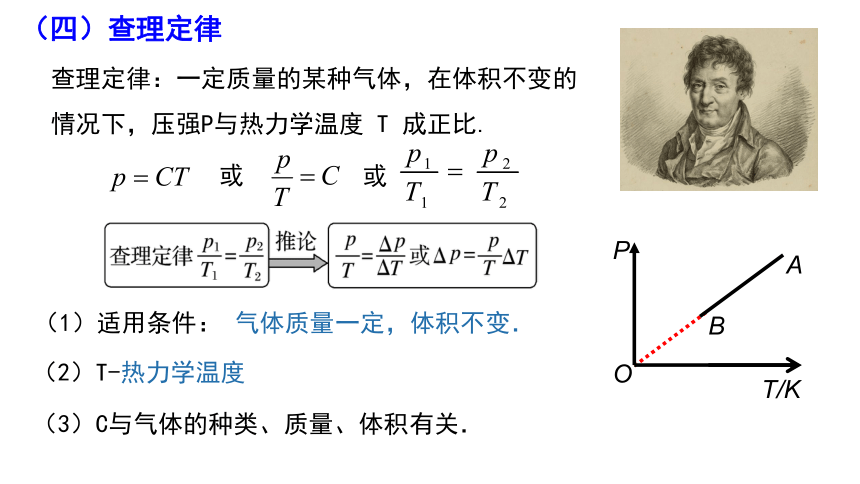
(四)查理定律
A
B
T/K
P
O
查理定律:一定质量的某种气体,在体积不变的情况下,压强P与热力学温度 T 成正比.
或
或
(1)适用条件: 气体质量一定,体积不变.
(2)T-热力学温度
(3)C与气体的种类、质量、体积有关.
(五)等容线(P-T图)
①点:确定的状态
③斜率:不同体积下的等容线,斜率越大,体积越小。如V2O
p
T
O
p
T
V2
V1
②线:变化过程;同一条等容线各状态体积相同
想一想:为什么O点附近用虚线?
——热力学绝对零度不可能达到。
延长线过原点的倾斜直线
讨论与交流
如何把鸡蛋从玻璃瓶内解救出来?
讨论与交流
夏天是个燥热的季节,也是交通事故频发的季节。请结合查理定律,分析夏季安全行车需要注意的事项有哪些呢?
——胎压监测装置
典例分析
例题1 汽车轮胎的气压是影响汽车节油及行驶安全的重要因素,据统计,在高速公路上有40%以上的交通事故是由于轮胎发生故障引起的。汽车在高速行驶时车胎因反复形变而升温,车胎内气压随之升高。某品牌的汽车轮胎说明书上标有“最大胎压3kg/cm2”.该车在夏天以120km/h的速度行驶时,车胎内气体温度可达70℃。为保证汽车在最高限速120 km/h的高速道路上安全行驶,则在30℃的气温下,汽车出发前给车胎充气的气压上限是多少?
分析:空气注入车胎后质量不变,忽略车胎体积变化--查理定律
设车胎30°C时能充的最大气压为P1,70°C时能充的最大气压为P2
等容变化
状态1
状态2
解得
根据查理定律:
知识回顾
一定质量的气体,其温度、体积和压强三个量之间存在某种关系。
探究气体等温变化的规律
探究三个量之间的变化关系?
控制变量法
探究气体等容变化的规律
探究气体等压变化的规律
—— 玻意耳定律
—— 查理定律
Part 02
探究气体等压变化的规律
(一)提出猜想
定性分析:
一定质量的某种气体,保持压强不变,当温度升高时,气体的体积增大;当温度降低时,气体的体积减小。
(二)实验探究
思考:①怎么保证等压变化? ②怎么测量体积和温度?
P=P0
移动压强计右侧玻璃管使得左右液面每次相平
(三)实验结论
实验结论:气体压强一定时,各种气体的气体都随温度的升高均匀增大。
O
V
t/
A
B
℃
外推
V=Ct+V0
-273.15℃
A
B
T/K
V
O
P=CT
热力学温度T=t+273.15 K
体积V与热力学温度 T 成正比
(四)盖-吕萨克定律
盖-吕萨克定律:一定质量的某种气体,在压强不变的情况下,体积 V 与热力学温度 T 成正比.
或
或
(1)适用条件:气体质量一定,压强不变.
(2)T-热力学温度
(3)C与气体的种类、质量、压强有关.
A
B
T/K
V
O
(五)等压线( V-T图):
①点:确定的状态
③斜率:不同压强下的等压线,斜率越大,压强越小。如P2O
V
T
O
V
T
P2
P1
②线:变化过程;同一条等压线各状态压强相同
延长线过原点的倾斜直线
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
分析:室外空气进入室内,使得室内外空气的压强保持动态的平衡(等压变化)
室内空气的质量增加、压强不变,则研究对象为从室外进入室内的空气与原来室内的空气看成一个整体(质量不变)
——盖-吕萨克定律
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
等压变化
研究对象:室外进入室内的空气与原来室内的空气
在0°C、33°C、26°C研究气体体积分别为V0、V1、V2
等压变化
状态1
状态2
等压变化
状态3
△m=ρ1(V1-V2)
ρ0 = 1.29kg/m3
ρ1=
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
等压变化
研究对象:室外进入室内的空气与原来室内的空气
在0°C、33°C、26°C研究气体体积分别为V0、V1、V2
根据盖-吕萨克定律:
设在33°C时空气密度为ρ1,0°C时空气密度为ρ0=1.29kg/m3
ρ0VO=ρ1V1
△m=ρ1(V1-V2)
解得
课堂小结
或
或
或
或
图线表达
应用 直线的斜率越大,体积越小,如图,V2<V1
盖-吕萨克定律(等压变化)
气体的质量一定,压强不变
直线的斜率越大,压强越小,如图,
p2<p1
定律 查理定律(等容变化)
表达式
成立条件 气体的质量一定,体积不变
气体实验定律
玻意耳定律
查理定律
盖-吕萨克定律
压强不太大(相对大气压),温度不太低(相对室温)
这些定律的适用范围:
p1V1=p2V2
例题:如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)
例题:如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)
[解析] 由题意可知,TD=(273+27)K=300 K
由题图可知,C→D为等容变化过程且pC=2×105 Pa,pD=1×105 Pa
根据查理定律可得TC=TD=×300 K=600 K
由题图可知,B→C为等温变化过程,TB=TC=600 K
由题图可知,A→B为等压变化过程,且VA=1 L,VB=2 L
根据盖-吕萨克定律可得TA=TB=×600 K=300 K
p -T图像如图所示.
第二章 气体、液体和固体
粤教版 选择性必修三
第一节 气体实验定律Ⅱ
知识回顾
一定质量的气体,其温度、体积和压强三个量之间存在某种关系。
探究气体等温变化的规律
探究三个量之间的变化关系?
控制变量法
探究气体等容变化的规律
探究气体等压变化的规律
—— 玻意耳定律
Part 01
探究气体等容变化的规律
(一)提出猜想
观察下列日常生活现象,猜想在等容变化中,气体的压强与温度可能存在着什么关系呢?
瓶吞鸡蛋
车辆在夏季容易爆胎
定性分析:
一定质量的某种气体,保持体积不变,当温度升高时,气体的压强增大;当温度降低时,气体的压强减小。
(二)实验探究
思考:①怎么保证等容变化? ②怎么测量压强和温度?
(二)实验探究
思考:①怎么保证等容变化? ②怎么测量压强和温度?
P1=P0
P2=P0-ρgh
P3=P0+ρgh
移动压强计右侧玻璃管使得左管上液面每次恢复到标记处
(三)实验结论
实验结论:气体体积一定时,各种气体的压强都随温度的升高均匀增大。
O
P
t/
A
B
℃
外推
P=Ct+P0
-273.15℃
A
B
T/K
P
O
P=CT
热力学温度T=t+273.15 K
简洁美
热力学温度(T),国际单位开尔文,简称开,符号K
压强P与热力学温度 T 成正比
(四)查理定律
A
B
T/K
P
O
查理定律:一定质量的某种气体,在体积不变的情况下,压强P与热力学温度 T 成正比.
或
或
(1)适用条件: 气体质量一定,体积不变.
(2)T-热力学温度
(3)C与气体的种类、质量、体积有关.
(五)等容线(P-T图)
①点:确定的状态
③斜率:不同体积下的等容线,斜率越大,体积越小。如V2
p
T
O
p
T
V2
V1
②线:变化过程;同一条等容线各状态体积相同
想一想:为什么O点附近用虚线?
——热力学绝对零度不可能达到。
延长线过原点的倾斜直线
讨论与交流
如何把鸡蛋从玻璃瓶内解救出来?
讨论与交流
夏天是个燥热的季节,也是交通事故频发的季节。请结合查理定律,分析夏季安全行车需要注意的事项有哪些呢?
——胎压监测装置
典例分析
例题1 汽车轮胎的气压是影响汽车节油及行驶安全的重要因素,据统计,在高速公路上有40%以上的交通事故是由于轮胎发生故障引起的。汽车在高速行驶时车胎因反复形变而升温,车胎内气压随之升高。某品牌的汽车轮胎说明书上标有“最大胎压3kg/cm2”.该车在夏天以120km/h的速度行驶时,车胎内气体温度可达70℃。为保证汽车在最高限速120 km/h的高速道路上安全行驶,则在30℃的气温下,汽车出发前给车胎充气的气压上限是多少?
分析:空气注入车胎后质量不变,忽略车胎体积变化--查理定律
设车胎30°C时能充的最大气压为P1,70°C时能充的最大气压为P2
等容变化
状态1
状态2
解得
根据查理定律:
知识回顾
一定质量的气体,其温度、体积和压强三个量之间存在某种关系。
探究气体等温变化的规律
探究三个量之间的变化关系?
控制变量法
探究气体等容变化的规律
探究气体等压变化的规律
—— 玻意耳定律
—— 查理定律
Part 02
探究气体等压变化的规律
(一)提出猜想
定性分析:
一定质量的某种气体,保持压强不变,当温度升高时,气体的体积增大;当温度降低时,气体的体积减小。
(二)实验探究
思考:①怎么保证等压变化? ②怎么测量体积和温度?
P=P0
移动压强计右侧玻璃管使得左右液面每次相平
(三)实验结论
实验结论:气体压强一定时,各种气体的气体都随温度的升高均匀增大。
O
V
t/
A
B
℃
外推
V=Ct+V0
-273.15℃
A
B
T/K
V
O
P=CT
热力学温度T=t+273.15 K
体积V与热力学温度 T 成正比
(四)盖-吕萨克定律
盖-吕萨克定律:一定质量的某种气体,在压强不变的情况下,体积 V 与热力学温度 T 成正比.
或
或
(1)适用条件:气体质量一定,压强不变.
(2)T-热力学温度
(3)C与气体的种类、质量、压强有关.
A
B
T/K
V
O
(五)等压线( V-T图):
①点:确定的状态
③斜率:不同压强下的等压线,斜率越大,压强越小。如P2
V
T
O
V
T
P2
P1
②线:变化过程;同一条等压线各状态压强相同
延长线过原点的倾斜直线
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
分析:室外空气进入室内,使得室内外空气的压强保持动态的平衡(等压变化)
室内空气的质量增加、压强不变,则研究对象为从室外进入室内的空气与原来室内的空气看成一个整体(质量不变)
——盖-吕萨克定律
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
等压变化
研究对象:室外进入室内的空气与原来室内的空气
在0°C、33°C、26°C研究气体体积分别为V0、V1、V2
等压变化
状态1
状态2
等压变化
状态3
△m=ρ1(V1-V2)
ρ0 = 1.29kg/m3
ρ1=
典例分析
例题2:炎热的夏天,当我们在教室开空调时,除了温度以外,教室内空气的质量其实也发生了改变。设教室长,宽,高分别为L=10 m,D=6m,H =3m,开空调使室内空气从温度t1=33℃降到t2=26℃,请估算降温前后教室内空气的质量变化量。
(已知1个标准大气压下,温度为0℃,空气密度为1.29kg/m3)
等压变化
研究对象:室外进入室内的空气与原来室内的空气
在0°C、33°C、26°C研究气体体积分别为V0、V1、V2
根据盖-吕萨克定律:
设在33°C时空气密度为ρ1,0°C时空气密度为ρ0=1.29kg/m3
ρ0VO=ρ1V1
△m=ρ1(V1-V2)
解得
课堂小结
或
或
或
或
图线表达
应用 直线的斜率越大,体积越小,如图,V2<V1
盖-吕萨克定律(等压变化)
气体的质量一定,压强不变
直线的斜率越大,压强越小,如图,
p2<p1
定律 查理定律(等容变化)
表达式
成立条件 气体的质量一定,体积不变
气体实验定律
玻意耳定律
查理定律
盖-吕萨克定律
压强不太大(相对大气压),温度不太低(相对室温)
这些定律的适用范围:
p1V1=p2V2
例题:如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)
例题:如图所示是一定质量的理想气体状态按图中箭头顺序变化,状态D的温度为27 ℃,BC为一段双曲线,试求出TA、TB、TC,并画出气体状态变化的p -T图像.(T=273 K+t)
[解析] 由题意可知,TD=(273+27)K=300 K
由题图可知,C→D为等容变化过程且pC=2×105 Pa,pD=1×105 Pa
根据查理定律可得TC=TD=×300 K=600 K
由题图可知,B→C为等温变化过程,TB=TC=600 K
由题图可知,A→B为等压变化过程,且VA=1 L,VB=2 L
根据盖-吕萨克定律可得TA=TB=×600 K=300 K
p -T图像如图所示.
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
