数学:7.2简单的轴对称图形同步练习1(北师大版七年级下)
文档属性
| 名称 | 数学:7.2简单的轴对称图形同步练习1(北师大版七年级下) |

|
|
| 格式 | rar | ||
| 文件大小 | 44.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
7.2 简单的轴对称图形(一) 同步练习
◆基础训练
一、选择题
1.下列图形中,不是轴对称图形的是( ).
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列图形中,是轴对称图形的有( )个.
①直角三角形,②线段,③等边三角形,④正方形,⑤等腰三角形,⑥圆,⑦直角.
A.4个 B.3个 C.5个 D.6个
3.下列说法正确的是( ).
A.轴对称图形是两个图形组成的 B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形;D.直角三角形一定是轴对称图形
二、填空题
4.如图,CD⊥OA,CE⊥OB,D、E为垂足.
(1)若∠1=∠2,则有___________;
(2)若CD=CE,则有___________.
5.等腰三角形的两内角的比为1:4,则底角的度数为_________.
三、解答题
6.如图,在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E和D,BE=6,
求△BCE的周长.
7.如图,已知在AB=AC,DB=DC,则AD⊥BC,为什么?
◆能力提高
一、填空题
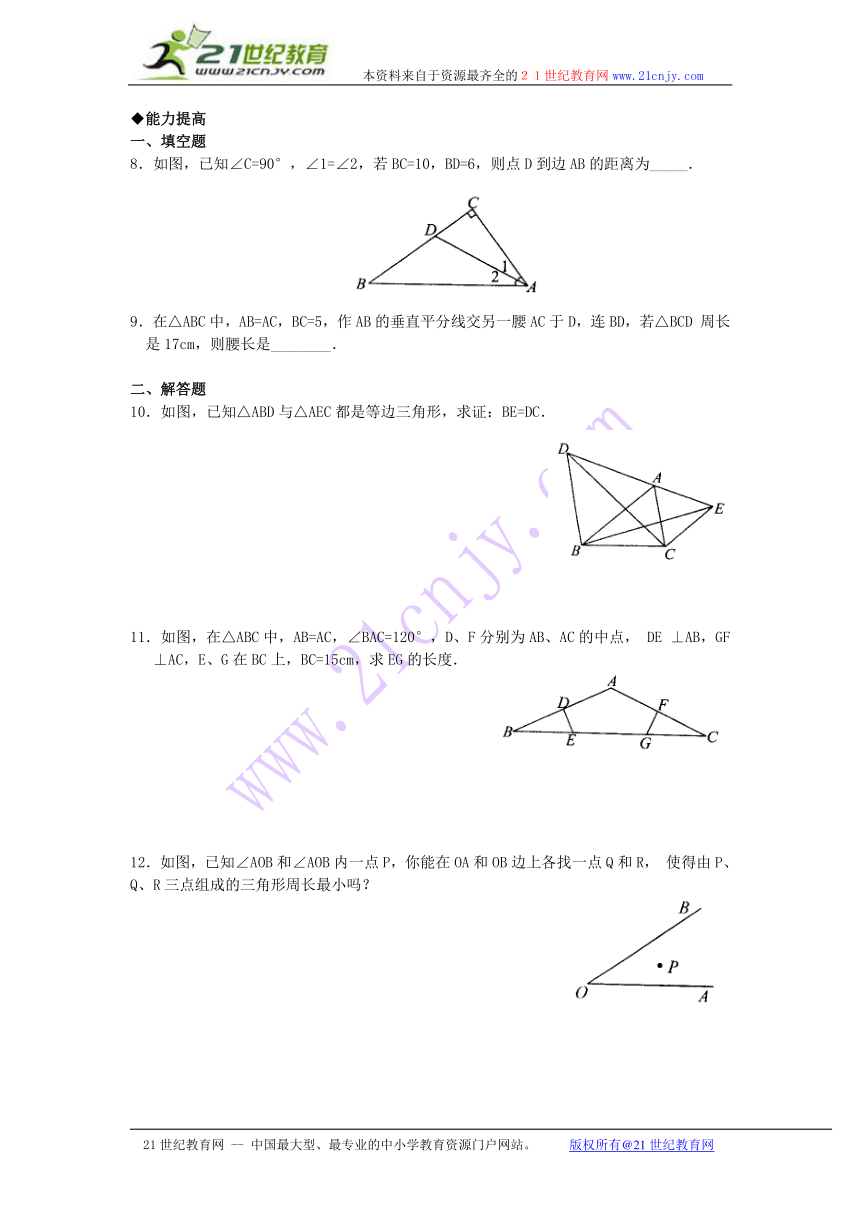
8.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为_____.
9.在△ABC中,AB=AC,BC=5,作AB的垂直平分线交另一腰AC于D,连BD,若△BCD周长是17cm,则腰长是________.
二、解答题
10.如图,已知△ABD与△AEC都是等边三角形,求证:BE=DC.
11.如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,DE⊥AB,GF⊥AC,E、G在BC上,BC=15cm,求EG的长度.
12.如图,已知∠AOB和∠AOB内一点P,你能在OA和OB边上各找一点Q和R,使得由P、Q、R三点组成的三角形周长最小吗?
答案:
1.D 2.D 3.B 4.(1)DC=EC;(2)∠1=∠2 5.30°或80° 6.22
7.证明△ABD≌△ACD 8.4 9.12cm 10.证明△ADC≌△ABE
11.连接AE、AG,则AE=BE,AG=CG,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,
∴∠AEG=∠AGE=60°,∴△AEG为等边三角形,∴AE=EG=AG=BE=CE,∴EG=BC=5cm.
12.作P点关于OB、OA的对称点P1、P2,连接P1P2,与OB交于R,与OA交于Q.
7.2 简单的轴对称图形(二)
◆基础训练
一、选择题
1.下列轴对称图形中,对称轴最多的是( ).
A.等腰三角形 B.等边三角形 C.正方形 D.线段
2.如图,在△ABC中,D、E分别是AC、BC上的点,且△ADB≌△EDB≌△EDC,则∠C=( ).
A.15° B.20° C.25° D.30°
3.下面给出几种三角形:(1)有两个角为60°的三角形;(2)三个外角都相等的三角形;(3)一边上的高也是这边上的中线的三角形;(4)有一个角为60°的等腰三角形,其中是等边三角形的个数是( ).
A.4个 B.3个 C.2个 D.1个
二、填空题
4.在△ABC中,若BC=AC,∠A=58°,则∠C=_____,∠B=________.
5.等边三角形的两条中线相交所成的钝角度数是_______.
三、解答题
6.如图,CE⊥AB于点E,BD⊥AC于D,BD、CE交点O,且AO平分∠BAC,求证:OB=OC.
7.如图,△ABC与△BDE都是等边三角形,求证:AE=CD.
◆能力提高
一、填空题
8.等腰△ABC中,AB的中垂线与AC所在直线相交成的锐角为50°,则底角B的大小为________.
9.如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=_______.
二、解答题
10.如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,
求证:BD+EC=DE.
11.如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
( http: / / www.21cnjy.com / )
12.如图,BC>AB,BD平分∠ABC且AD=DC.求证:∠A+∠C=180°.
答案:
1.C 2.D 3.B 4.64°,58° 5.120°
6.证明△OBE≌△OCD 7.证明△ABE≌△CBD
8.70°或20° 9.120°
10.∵BF平分∠ABC,∴∠DBF=∠FBC.
∵DE∥BC,∴∠DFB=∠FBC,∠DBF=∠DFB,
∴DF=DB,同理FE=EC,∴DE=DF+FE=BD+EC.
11.设∠A=x,∵AD=DE=EB,∴∠DEA=∠A=x,∠EBD=∠EDB.
又∵∠DEA=∠EBD+∠EDB,
∴∠EBD=∠EDB=,
∴∠BDC=∠A+∠ABD=x.
∵DB=BD,AB=AC,
∴∠BDC=∠BCD=∠ABC=x.
又∠A+∠ABC+∠ACB=180°,
∴x+x+x=180°,∴x=45°即∠A=45°.
12.证法一:在BC上取BE=AB,连DE,易证△ABD≌△EBD,
∴∠A=∠DEB,DE=AD.
又AD=DC,
∴DE=DC,∴∠DEC=∠C.
而∠DEB+∠DEC=180°,
∴∠A+∠C=180°.
证法二,延长BA至F,使BF=BC,易证△FBD≌△CBD,
∴∠C=∠F,CD=DF.
又CD=AD,∴DF=AD,
∴∠F=∠FAD,∴∠C=∠FAD.
又∠BAD+∠FAD=180°,
∴∠BAD+∠C=180°.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
7.2 简单的轴对称图形(一) 同步练习
◆基础训练
一、选择题
1.下列图形中,不是轴对称图形的是( ).
A.角 B.等边三角形 C.线段 D.平行四边形
2.下列图形中,是轴对称图形的有( )个.
①直角三角形,②线段,③等边三角形,④正方形,⑤等腰三角形,⑥圆,⑦直角.
A.4个 B.3个 C.5个 D.6个
3.下列说法正确的是( ).
A.轴对称图形是两个图形组成的 B.等边三角形有三条对称轴
C.两个全等的三角形组成一个轴对称图形;D.直角三角形一定是轴对称图形
二、填空题
4.如图,CD⊥OA,CE⊥OB,D、E为垂足.
(1)若∠1=∠2,则有___________;
(2)若CD=CE,则有___________.
5.等腰三角形的两内角的比为1:4,则底角的度数为_________.
三、解答题
6.如图,在△ABC中,BC=10,边BC的垂直平分线分别交AB,BC于点E和D,BE=6,
求△BCE的周长.
7.如图,已知在AB=AC,DB=DC,则AD⊥BC,为什么?
◆能力提高
一、填空题
8.如图,已知∠C=90°,∠1=∠2,若BC=10,BD=6,则点D到边AB的距离为_____.
9.在△ABC中,AB=AC,BC=5,作AB的垂直平分线交另一腰AC于D,连BD,若△BCD周长是17cm,则腰长是________.
二、解答题
10.如图,已知△ABD与△AEC都是等边三角形,求证:BE=DC.
11.如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,DE⊥AB,GF⊥AC,E、G在BC上,BC=15cm,求EG的长度.
12.如图,已知∠AOB和∠AOB内一点P,你能在OA和OB边上各找一点Q和R,使得由P、Q、R三点组成的三角形周长最小吗?
答案:
1.D 2.D 3.B 4.(1)DC=EC;(2)∠1=∠2 5.30°或80° 6.22
7.证明△ABD≌△ACD 8.4 9.12cm 10.证明△ADC≌△ABE
11.连接AE、AG,则AE=BE,AG=CG,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,
∴∠AEG=∠AGE=60°,∴△AEG为等边三角形,∴AE=EG=AG=BE=CE,∴EG=BC=5cm.
12.作P点关于OB、OA的对称点P1、P2,连接P1P2,与OB交于R,与OA交于Q.
7.2 简单的轴对称图形(二)
◆基础训练
一、选择题
1.下列轴对称图形中,对称轴最多的是( ).
A.等腰三角形 B.等边三角形 C.正方形 D.线段
2.如图,在△ABC中,D、E分别是AC、BC上的点,且△ADB≌△EDB≌△EDC,则∠C=( ).
A.15° B.20° C.25° D.30°
3.下面给出几种三角形:(1)有两个角为60°的三角形;(2)三个外角都相等的三角形;(3)一边上的高也是这边上的中线的三角形;(4)有一个角为60°的等腰三角形,其中是等边三角形的个数是( ).
A.4个 B.3个 C.2个 D.1个
二、填空题
4.在△ABC中,若BC=AC,∠A=58°,则∠C=_____,∠B=________.
5.等边三角形的两条中线相交所成的钝角度数是_______.
三、解答题
6.如图,CE⊥AB于点E,BD⊥AC于D,BD、CE交点O,且AO平分∠BAC,求证:OB=OC.
7.如图,△ABC与△BDE都是等边三角形,求证:AE=CD.
◆能力提高
一、填空题
8.等腰△ABC中,AB的中垂线与AC所在直线相交成的锐角为50°,则底角B的大小为________.
9.如图,P、Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=_______.
二、解答题
10.如图,∠ABC与∠ACB的平分线相交于F,过F作DE∥BC交AB于D,交AC于E,
求证:BD+EC=DE.
11.如图,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=BE,求∠A的度数.
( http: / / www.21cnjy.com / )
12.如图,BC>AB,BD平分∠ABC且AD=DC.求证:∠A+∠C=180°.
答案:
1.C 2.D 3.B 4.64°,58° 5.120°
6.证明△OBE≌△OCD 7.证明△ABE≌△CBD
8.70°或20° 9.120°
10.∵BF平分∠ABC,∴∠DBF=∠FBC.
∵DE∥BC,∴∠DFB=∠FBC,∠DBF=∠DFB,
∴DF=DB,同理FE=EC,∴DE=DF+FE=BD+EC.
11.设∠A=x,∵AD=DE=EB,∴∠DEA=∠A=x,∠EBD=∠EDB.
又∵∠DEA=∠EBD+∠EDB,
∴∠EBD=∠EDB=,
∴∠BDC=∠A+∠ABD=x.
∵DB=BD,AB=AC,
∴∠BDC=∠BCD=∠ABC=x.
又∠A+∠ABC+∠ACB=180°,
∴x+x+x=180°,∴x=45°即∠A=45°.
12.证法一:在BC上取BE=AB,连DE,易证△ABD≌△EBD,
∴∠A=∠DEB,DE=AD.
又AD=DC,
∴DE=DC,∴∠DEC=∠C.
而∠DEB+∠DEC=180°,
∴∠A+∠C=180°.
证法二,延长BA至F,使BF=BC,易证△FBD≌△CBD,
∴∠C=∠F,CD=DF.
又CD=AD,∴DF=AD,
∴∠F=∠FAD,∴∠C=∠FAD.
又∠BAD+∠FAD=180°,
∴∠BAD+∠C=180°.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
