2024年高一数学暑假必修一预学课 第一章复习知识点
文档属性
| 名称 | 2024年高一数学暑假必修一预学课 第一章复习知识点 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 08:54:51 | ||
图片预览










文档简介
(共38张PPT)
章末复习
1.集合的含义和表示
(1)了解集合的含义,元素与集合的”属于”关系;
(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.集合间的基本运算
(1)理解集合之间包含与相等的含义,能识别给定集合的子集;
(2)在具体情境下,了解全集和空集的含义.
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;
(3)能使用韦恩图表达集合的关系和运算.
一、元素与集合
1.集合中元素的三个特性:① 、② 、③ .
2.集合中元素与集合的关系
元素与集合之间的关系有④ 和⑤ 两种,表示符号为⑥ 和⑦ .
3.常见集合的符号表示
集合 自然数集 正整数集 整数集 有理
数集 实数集
表示 ⑧ . ⑨ . ⑩ . . .
4.集合的表示法: 、 、 .
互异性
确定性
无序性
属于
不属于
列举法
描述法
∈
N
N*或N+
Z
Q
R
Venn图
1.集合A={x|y= }、B={y|y= },A、B相等吗?
提示 不相等.A中的代表元素是x,故A是y= 的定义域,A={x|x≥1},B中的代表元素是y,
故B是y= 的值域,∴B={y|y≥0},所以A≠B
二、集合间的基本关系
A=B
A B
或B A
A?B
或B?A
表示关系 定义 记法
集合
间的
基本
关系 相等 集合A与集合B中的所有元素都相同 .
子集 A中任意一元素均为B中的元素
.
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有 .
A
非空集合
?B(B≠ )
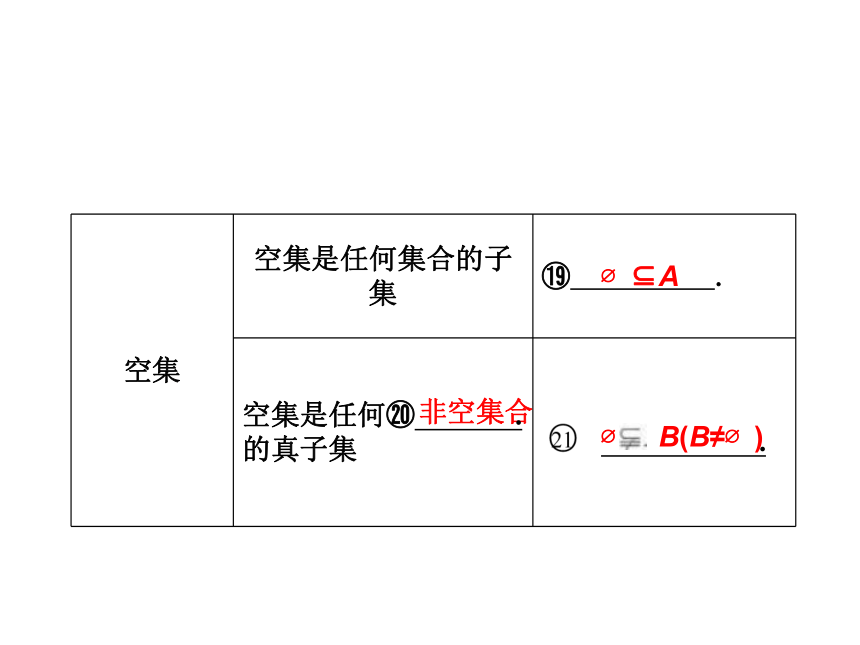
空集 空集是任何集合的子集 .
空集是任何 . 的真子集 .
2.集合{ }是空集吗?它与集合{0}有什么区别?
提示 集合{ }不是空集.空集是不含任何元素的集合,而集合{ }中有一个元素 ,集合{ }与集合{0}的区别是它们的元素不同,其中{ }的元素为 ,{0}的元素为0.
3.子集与真子集有何区别和联系?
提示 集合A的真子集一定是其子集,而集合A的子集不一定是其真子集,还可以是集合A本身;若集合A有n个元素,则其子集的个数为2n个,真子集的个数为2n-1个.
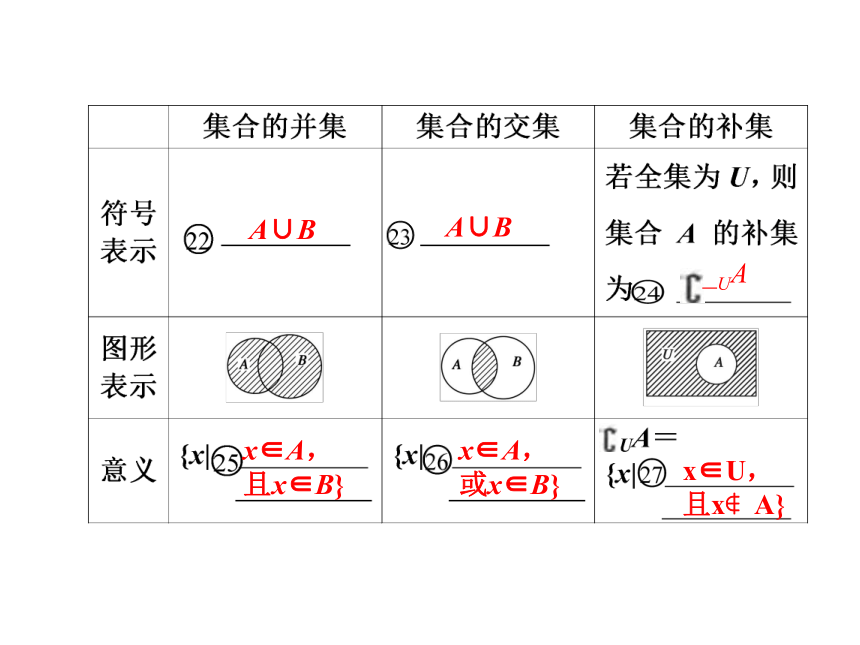
A∪B
_UA
A∪B
x∈A,
或x∈B}
x∈A,
且x∈B}
x∈U,
且x A}
A B
( _UA)∩ UB)
U A)∪ UB);
A B
A
A
A
∪
4.如何理解并集概念中的”或”?
提示 并集的概念中”x∈A或x∈B”包括三层意思:
x∈A,但x B;x A,但x∈B;x∈A且x∈B.
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},
则A∩( NB )为( )
A.{1,5,7} B.{3,5,7}
C.{1,3,9} D.{1,2,3}
【解析】 显然A∩( NB )= A(A∩B),
且A∩B={3,9},所以结果为{1,5,7}.
【答案】 A
【解析】 由题意M=(1,+∞),N=(0,2),
则M∩N=(1,2),故选A.
【答案】 A
2.(2011·东北四校模拟)已知集合M={y|y=2x ,
x>0},N={x|y=lg(2x-x2 )},则M∩N为( )
A.(1,2) B.(1,+∞)
C.[2,+∞) D.[1,+∞)
3.设集合A={5,log2(a+3) },集合B={a,b}.
若A∩B={2},则A∪B=________.
【解析】 ∵A∩B={2},∴ log2(a+3) =2.
∴a=1.∴b=2.
∴A={5,2},B={1,2}.
∴A∪B={1,2,5}.
【答案】 {1,2,5}
4.已知集合P={1,2},那么满足Q P的集合Q的个数是( )
A.4 B.3
C.2 D.1
【解析】 ∵Q P,P={1,2},
∴Q= ,{1},{2},{1,2}.
【答案】 A
5.(2011·江苏模拟)已知全集U=R,集合A={x|log2(3-x) ≤2},集合B= .
(1)求集合A、B;
(2)求( UA )∩B.
【解析】 (1)由已知得log2(3-x)≤log24,∴ 解得-1≤x<3,
∴A={x|-1≤x<3}.
由 ≥1,得(x+2)(x-3)≤0,
且x+2≠0,解得-2<x≤3.
∴B={x|-2<x≤3}.
(2)由(1)可得 UA={x|x<-1或x≥3}.
故( UA)∩B={x|-2<x<-1或x=3}.
1.掌握集合的概念,关键是把握集合中元素的特性,要特别注意集合中元素的互异性,一方面利用集合元素的互异性能顺利找到解题的切入点;另一方面,在解答完毕之时,注意检验集合的元素是否满足互异性以确保答案正确.
2.用描述法表示集合时,首先应清楚集合的类型和元素的性质.如集合{y|y=2x },{x|y= 2x},{(x,y)|y= 2x}表示不同的集合.
(2011·高考改编题)已知a,b∈R,{a, ,1}={a2,a+b,0},则a2012+b2012=________.
【思路点拨】 利用集合相等的概念求出a,b,然后计算
【解析】 由已知得 =0且a≠0,所以b=0,
于是a2=1,即a=1或a=-1.
当a=1时,两集合中的元素分别为1,0,1与1,1,0不满足集合中元素的互异性,故a≠1,
∴a=-1,此时集合为{-1,0,1},符合题意,
∴a2012+b2012=(-1)2012+02012=1.
【答案】 1
【发散思维】 在利用集合相等或其他相关概念求字母的值时,特别需注意利用集合中元素的互异性来检验所得结果是否正确.
1.集合A={0,2,a},B={1,a2 },
若A∪B={0,1,2,4,16}则a的值为( )
A.0 B.1
C.2 D.4
【解析】 a=4时, a2 =16,A={0,2,4},
B={1,16}; a2 =4,a=±2,不满足题意,故选D.
【答案】 D
在解决两个集合的关系问题时,避免出错的一个有效手段即是合理运用数轴或韦恩图来帮助分析和求解,另外,在解含有参数的不等式(或方程)时,要对参数进行讨论,分类时要遵循”不重不漏”的分类原则,然后对于每一类情况都要给出问题的解答.
(2010·浙江高考)设P={x|x<4},
Q={x|x2<4},则( )
A.P Q B.Q P
C.P RQ D.Q RP
【思路点拨】 可先化简Q,再判断P与Q的关系.
【解析】 Q={x|-2<x<2},如图所示,则Q P.
【答案】 B
【发散思维】 判断两集合间的关系,实际上是判断两集合元素的关系,故首先需先求出两个集合,使其明晰化,然后利用韦恩图法、数轴法或图象法来判断.
2.(2011·海淀模拟)已知集合S= ,
P={x|a+1<x<2a+15}.
(1)求集合S;
(2)若S P,求实数a的取值范围.
【解析】
(1)由 <0得-2<x<5,∴S={x|-2<x<5}
(2)由S P得 解之得-5≤a≤-3.
解决集合的运算问题,一般先化简集合以确定集合的元素,然后借助韦恩图和数轴等使抽象问题直观化.一般地,集合元素离散时用韦恩图表示,集合元素连续时用数轴表示,用数轴表示时需注意端点值的取舍.
(2010·天津高考)设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R}.若A∩B= ,则实数a的取值范围是( )
A.{a|0≤a≤6} B.{a|a≤2或a≥4}
C.{a|a≤0或a≥6} D.{a|2≤a≤4}
【思路点拨】 借助数轴画图分析.
【解析】 A={x||x-a|<1,x∈R}
={x|a-1<x<1+a},∵A∩B= ,如图所示
或
∴a+1≤1或a-1≥5即a≤0或a≥6.
【答案】 C
【发散思维】 在进行集合的运算时,先看清集合的元素和所满足的条件,再把所给集合化为最简形式,并合理转化求解,必要时充分利用数轴、韦恩图、图象等工具,并会运用分类讨论、数形结合等思想方法,使运算更加直观,简洁.
3.(2011·宣武模拟)设S为全集,B A S,
则下列结论中正确的是( )
A. SA SB B.A∩B=B
C.A∩( SB)= D.A∪B=S
【解析】 利用韦恩图可知,B正确.
【答案】 B
新概念的引入不仅要求能深入理解新概念的信息,而且要能够调出已学习过的”旧”概念,进行相互对照,此类考题的关键在于一个”新”字,即背景新、概念新、题型新,解题时不要被”新”所迷惑,在理解与领会概念后,掩藏在”新”的外衣下的往往是极为简单的知识点.
非空集合G关于运算 满足:(1)对任意的a,b∈G,都有a b∈G;(2)存在e∈G,使得对一切a∈G都有a e=e a=a,则称G关于运算 为”融洽集”.现给出下列集合和运算:
①G={非负整数}, 为整数的加法;
②G={偶数}, 为整数的乘法;
③G={平面向量}, 为平面向量的加法;
④G={二次三项式}, 为多项式的加法;
⑤G={虚数}, 为复数的乘法.
其中G关于运算 为”融洽集”的有哪些?
并说明理由.
【思路点拨】 充分理解”融洽集”的概念要求,而后将①②③④⑤逐一验证是否符合条件即可.
【解析】 ①G={非负整数}, 为整数的加法.
∵任意两个非负整数的和仍为非负整数,且存在e=0,使得对一切a∈G,都有a 0=0 a=a,
∴①符合G关于运算 为”融洽集”;2分
②G={偶数}, 为整数的乘法.
∵任意两个偶数的乘积仍是偶数,但不存在偶数e∈G使得对一切a∈G都有a e=e a=a成立,
∴②不符合G关于运算 为”融洽集”;4分
③G={平面向量}, 为平面向量的加法.
∵任意两个向量之和仍为向量,且存在e=0,使得对一切a∈G都有a 0=0 a=a,
∴③符合G关于运算 为”融洽集”;7分
④G={二次三项式}, 为多项式的加法.
∵任意两个二次三项式的和不一定是二次三项式,
∴④不符合G关于运算 为”融洽集”;9分
⑤G={虚数}, 为复数的乘法.
∵任意两个虚数的乘积不一定是虚数,
∴⑤不符合G关于运算 为”融洽集”.11分
综上所述,其中G关于运算 为”融洽集”的有①③.
12分
【发散思维】 新型集合的概念及运算问题是近几年新课标高考的热点问题.在给出新的运算法则的前提下,充分利用已知求解是关键.集合命题中与运算法则相关的问题,是对映射构建下的集合与集合、元素与元素间的运算相关性及封闭性的研究.
4.对任意两个正整数m,n定义某种运算 :
m n=
则集合P={(a,b)|a b=8,a,b∈N+}中元素的
个数为( )
A.5 B.7
C.9 D.11
【解析】 由运算 的定义知共有
(2,6),(1,7),(3,5),(4,4),(1,8),(6,2),
(7,1),(5,3),(8,1).
【答案】 C
章末复习
1.集合的含义和表示
(1)了解集合的含义,元素与集合的”属于”关系;
(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.
2.集合间的基本运算
(1)理解集合之间包含与相等的含义,能识别给定集合的子集;
(2)在具体情境下,了解全集和空集的含义.
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;
(3)能使用韦恩图表达集合的关系和运算.
一、元素与集合
1.集合中元素的三个特性:① 、② 、③ .
2.集合中元素与集合的关系
元素与集合之间的关系有④ 和⑤ 两种,表示符号为⑥ 和⑦ .
3.常见集合的符号表示
集合 自然数集 正整数集 整数集 有理
数集 实数集
表示 ⑧ . ⑨ . ⑩ . . .
4.集合的表示法: 、 、 .
互异性
确定性
无序性
属于
不属于
列举法
描述法
∈
N
N*或N+
Z
Q
R
Venn图
1.集合A={x|y= }、B={y|y= },A、B相等吗?
提示 不相等.A中的代表元素是x,故A是y= 的定义域,A={x|x≥1},B中的代表元素是y,
故B是y= 的值域,∴B={y|y≥0},所以A≠B
二、集合间的基本关系
A=B
A B
或B A
A?B
或B?A
表示关系 定义 记法
集合
间的
基本
关系 相等 集合A与集合B中的所有元素都相同 .
子集 A中任意一元素均为B中的元素
.
真子集 A中任意一元素均为B中的元素,且B中至少有一个元素A中没有 .
A
非空集合
?B(B≠ )
空集 空集是任何集合的子集 .
空集是任何 . 的真子集 .
2.集合{ }是空集吗?它与集合{0}有什么区别?
提示 集合{ }不是空集.空集是不含任何元素的集合,而集合{ }中有一个元素 ,集合{ }与集合{0}的区别是它们的元素不同,其中{ }的元素为 ,{0}的元素为0.
3.子集与真子集有何区别和联系?
提示 集合A的真子集一定是其子集,而集合A的子集不一定是其真子集,还可以是集合A本身;若集合A有n个元素,则其子集的个数为2n个,真子集的个数为2n-1个.
A∪B
_UA
A∪B
x∈A,
或x∈B}
x∈A,
且x∈B}
x∈U,
且x A}
A B
( _UA)∩ UB)
U A)∪ UB);
A B
A
A
A
∪
4.如何理解并集概念中的”或”?
提示 并集的概念中”x∈A或x∈B”包括三层意思:
x∈A,但x B;x A,但x∈B;x∈A且x∈B.
1.已知集合A={1,3,5,7,9},B={0,3,6,9,12},
则A∩( NB )为( )
A.{1,5,7} B.{3,5,7}
C.{1,3,9} D.{1,2,3}
【解析】 显然A∩( NB )= A(A∩B),
且A∩B={3,9},所以结果为{1,5,7}.
【答案】 A
【解析】 由题意M=(1,+∞),N=(0,2),
则M∩N=(1,2),故选A.
【答案】 A
2.(2011·东北四校模拟)已知集合M={y|y=2x ,
x>0},N={x|y=lg(2x-x2 )},则M∩N为( )
A.(1,2) B.(1,+∞)
C.[2,+∞) D.[1,+∞)
3.设集合A={5,log2(a+3) },集合B={a,b}.
若A∩B={2},则A∪B=________.
【解析】 ∵A∩B={2},∴ log2(a+3) =2.
∴a=1.∴b=2.
∴A={5,2},B={1,2}.
∴A∪B={1,2,5}.
【答案】 {1,2,5}
4.已知集合P={1,2},那么满足Q P的集合Q的个数是( )
A.4 B.3
C.2 D.1
【解析】 ∵Q P,P={1,2},
∴Q= ,{1},{2},{1,2}.
【答案】 A
5.(2011·江苏模拟)已知全集U=R,集合A={x|log2(3-x) ≤2},集合B= .
(1)求集合A、B;
(2)求( UA )∩B.
【解析】 (1)由已知得log2(3-x)≤log24,∴ 解得-1≤x<3,
∴A={x|-1≤x<3}.
由 ≥1,得(x+2)(x-3)≤0,
且x+2≠0,解得-2<x≤3.
∴B={x|-2<x≤3}.
(2)由(1)可得 UA={x|x<-1或x≥3}.
故( UA)∩B={x|-2<x<-1或x=3}.
1.掌握集合的概念,关键是把握集合中元素的特性,要特别注意集合中元素的互异性,一方面利用集合元素的互异性能顺利找到解题的切入点;另一方面,在解答完毕之时,注意检验集合的元素是否满足互异性以确保答案正确.
2.用描述法表示集合时,首先应清楚集合的类型和元素的性质.如集合{y|y=2x },{x|y= 2x},{(x,y)|y= 2x}表示不同的集合.
(2011·高考改编题)已知a,b∈R,{a, ,1}={a2,a+b,0},则a2012+b2012=________.
【思路点拨】 利用集合相等的概念求出a,b,然后计算
【解析】 由已知得 =0且a≠0,所以b=0,
于是a2=1,即a=1或a=-1.
当a=1时,两集合中的元素分别为1,0,1与1,1,0不满足集合中元素的互异性,故a≠1,
∴a=-1,此时集合为{-1,0,1},符合题意,
∴a2012+b2012=(-1)2012+02012=1.
【答案】 1
【发散思维】 在利用集合相等或其他相关概念求字母的值时,特别需注意利用集合中元素的互异性来检验所得结果是否正确.
1.集合A={0,2,a},B={1,a2 },
若A∪B={0,1,2,4,16}则a的值为( )
A.0 B.1
C.2 D.4
【解析】 a=4时, a2 =16,A={0,2,4},
B={1,16}; a2 =4,a=±2,不满足题意,故选D.
【答案】 D
在解决两个集合的关系问题时,避免出错的一个有效手段即是合理运用数轴或韦恩图来帮助分析和求解,另外,在解含有参数的不等式(或方程)时,要对参数进行讨论,分类时要遵循”不重不漏”的分类原则,然后对于每一类情况都要给出问题的解答.
(2010·浙江高考)设P={x|x<4},
Q={x|x2<4},则( )
A.P Q B.Q P
C.P RQ D.Q RP
【思路点拨】 可先化简Q,再判断P与Q的关系.
【解析】 Q={x|-2<x<2},如图所示,则Q P.
【答案】 B
【发散思维】 判断两集合间的关系,实际上是判断两集合元素的关系,故首先需先求出两个集合,使其明晰化,然后利用韦恩图法、数轴法或图象法来判断.
2.(2011·海淀模拟)已知集合S= ,
P={x|a+1<x<2a+15}.
(1)求集合S;
(2)若S P,求实数a的取值范围.
【解析】
(1)由 <0得-2<x<5,∴S={x|-2<x<5}
(2)由S P得 解之得-5≤a≤-3.
解决集合的运算问题,一般先化简集合以确定集合的元素,然后借助韦恩图和数轴等使抽象问题直观化.一般地,集合元素离散时用韦恩图表示,集合元素连续时用数轴表示,用数轴表示时需注意端点值的取舍.
(2010·天津高考)设集合A={x||x-a|<1,x∈R},B={x|1<x<5,x∈R}.若A∩B= ,则实数a的取值范围是( )
A.{a|0≤a≤6} B.{a|a≤2或a≥4}
C.{a|a≤0或a≥6} D.{a|2≤a≤4}
【思路点拨】 借助数轴画图分析.
【解析】 A={x||x-a|<1,x∈R}
={x|a-1<x<1+a},∵A∩B= ,如图所示
或
∴a+1≤1或a-1≥5即a≤0或a≥6.
【答案】 C
【发散思维】 在进行集合的运算时,先看清集合的元素和所满足的条件,再把所给集合化为最简形式,并合理转化求解,必要时充分利用数轴、韦恩图、图象等工具,并会运用分类讨论、数形结合等思想方法,使运算更加直观,简洁.
3.(2011·宣武模拟)设S为全集,B A S,
则下列结论中正确的是( )
A. SA SB B.A∩B=B
C.A∩( SB)= D.A∪B=S
【解析】 利用韦恩图可知,B正确.
【答案】 B
新概念的引入不仅要求能深入理解新概念的信息,而且要能够调出已学习过的”旧”概念,进行相互对照,此类考题的关键在于一个”新”字,即背景新、概念新、题型新,解题时不要被”新”所迷惑,在理解与领会概念后,掩藏在”新”的外衣下的往往是极为简单的知识点.
非空集合G关于运算 满足:(1)对任意的a,b∈G,都有a b∈G;(2)存在e∈G,使得对一切a∈G都有a e=e a=a,则称G关于运算 为”融洽集”.现给出下列集合和运算:
①G={非负整数}, 为整数的加法;
②G={偶数}, 为整数的乘法;
③G={平面向量}, 为平面向量的加法;
④G={二次三项式}, 为多项式的加法;
⑤G={虚数}, 为复数的乘法.
其中G关于运算 为”融洽集”的有哪些?
并说明理由.
【思路点拨】 充分理解”融洽集”的概念要求,而后将①②③④⑤逐一验证是否符合条件即可.
【解析】 ①G={非负整数}, 为整数的加法.
∵任意两个非负整数的和仍为非负整数,且存在e=0,使得对一切a∈G,都有a 0=0 a=a,
∴①符合G关于运算 为”融洽集”;2分
②G={偶数}, 为整数的乘法.
∵任意两个偶数的乘积仍是偶数,但不存在偶数e∈G使得对一切a∈G都有a e=e a=a成立,
∴②不符合G关于运算 为”融洽集”;4分
③G={平面向量}, 为平面向量的加法.
∵任意两个向量之和仍为向量,且存在e=0,使得对一切a∈G都有a 0=0 a=a,
∴③符合G关于运算 为”融洽集”;7分
④G={二次三项式}, 为多项式的加法.
∵任意两个二次三项式的和不一定是二次三项式,
∴④不符合G关于运算 为”融洽集”;9分
⑤G={虚数}, 为复数的乘法.
∵任意两个虚数的乘积不一定是虚数,
∴⑤不符合G关于运算 为”融洽集”.11分
综上所述,其中G关于运算 为”融洽集”的有①③.
12分
【发散思维】 新型集合的概念及运算问题是近几年新课标高考的热点问题.在给出新的运算法则的前提下,充分利用已知求解是关键.集合命题中与运算法则相关的问题,是对映射构建下的集合与集合、元素与元素间的运算相关性及封闭性的研究.
4.对任意两个正整数m,n定义某种运算 :
m n=
则集合P={(a,b)|a b=8,a,b∈N+}中元素的
个数为( )
A.5 B.7
C.9 D.11
【解析】 由运算 的定义知共有
(2,6),(1,7),(3,5),(4,4),(1,8),(6,2),
(7,1),(5,3),(8,1).
【答案】 C
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
