北师大版数学六年级下册 反比例 课件(21张PPT)
文档属性
| 名称 | 北师大版数学六年级下册 反比例 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
反比例
年 级:六年级
学 科:小学数学(北师大版)
第四单元
第5课时
反比例
想一想:怎样的两个量成正比例?
1.两个相关联的量;
2.一个量变化,另一个量也随着变化;
3.两个量中相对应的两个数的比值一定;
4. (一定);
反比例
猜一猜:怎样的两个量成反比例?
1.两个相关联的量
2.一个量变化,另一个量跟着变化
3.两个量的乘积一定
?
学习活动任务一:两个量的变化规律
①填一填:自学课本46页,并把表1、表2补充完整。
③比一比:他们之间的变化规律相同吗?有什么异同点?
②说一说:仔细观察,你发现了什么?
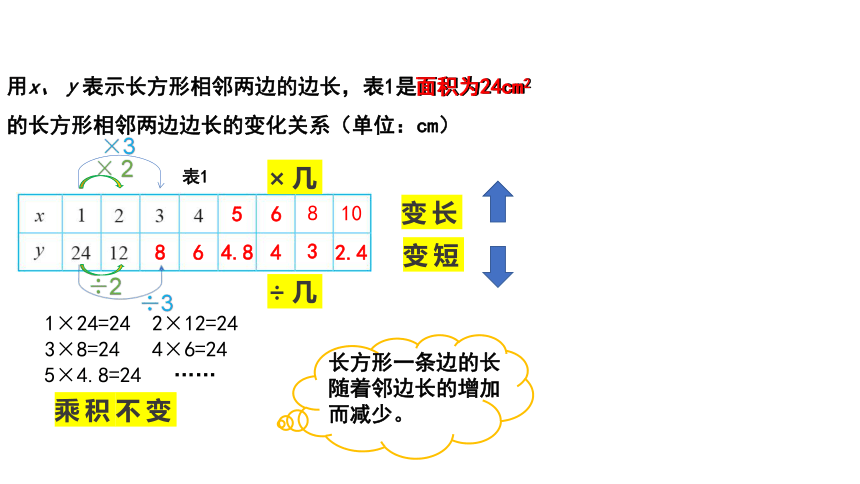
用x、у表示长方形相邻两边的边长,表1是面积为24cm2
的长方形相邻两边边长的变化关系(单位:cm)
表1
8
6
5
4.8
6
4
8
3
10
2.4
长方形一条边的长随着邻边长的增加而减少。
变长
变短
1×24=24 2×12=24
3×8=24 4×6=24 5×4.8=24 ……
乘积不变
× 2
÷2
×3
÷3
×几
÷几
面积为24cm2
用x、у表示长方形相邻两边的边长,表2是周长为24cm
的长方形相邻两边边长的变化关系(单位:cm)
表2
长方形一条边的长随着邻边长的增加而减少。
变长
变短
1+11=12 2+10=12
3+9=12 4+8=12 5+7=12 ……
和不变
+1
-1
+2
-2
+几
-几
周长为24cm
9
8
5
7
6
6
7
5
8
4
用x、у表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
9
8
5
7
6
6
7
5
8
4
8
6
5
4.8
6
4
8
3
10
2.4
两个相关联的量
一个量变化,另一个量跟着变化。
乘积一定
和一定
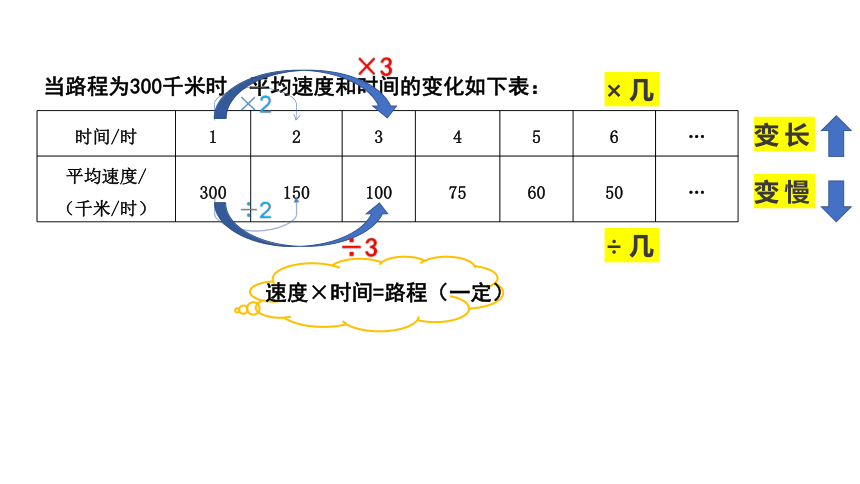
时间/时 1 2 3 4 5 6 …
平均速度/ (千米/时) 300 150 100 75 60 50 …
当路程为300千米时,平均速度和时间的变化如下表:
速度×时间=路程(一定)
×2
÷2
×3
÷3
×几
÷几
变长
变慢
二、自主学习,构建新知
时间/时 1 2 3 4 5 6 …
平均速度/ (千米/时) 300 150 100 75 60 50 …
当路程为300千米时,平均速度和时间的变化如下表:
小结
像这样,两种相关联的量,一个量变化,另一个量也随着变化,而且这两个量中相对应的两个数的乘积一定,我们就说这两个量成反比例。
表1
8
6
5
4.8
6
4
8
3
10
2.4
速度×时间=路程(一定)
速度和时间成反比例
长×宽=长方形的面积(一定)
长和宽成反比例
用x、у表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表2
9
8
5
7
6
6
7
5
8
4
表2中的长方形相邻两边的长成反比例吗?为什么?
表1
8
6
5
4.8
6
4
8
3
10
2.4
乘积一定
和一定
表2不成反比例
速度×时间=路程(一定)
路程一定,速度和时间成反比例。
时间一定或速度一定
成什么比例呢?
路程÷速度=时间,时间一定,路程和速度成正比例。
路程÷时间=速度,速度一定,路程和时间成正比例。
300:1=300 600:2=300 900:3=300 ……
100:50=2 200:100=2 300:150=2 ……
速度×时间=路程,路程一定,速度和时间成反比例。
反比例
正比例
1×300=300
2×150=300
……
300÷1=300
600÷2=300
……
100÷50=2
200÷100=2
……
相同点 不同点
正比例
反比例
学习活动任务二:正、反比例异同点
1.想一想:他们的特征分别是什么?
2.比一比:他们有什么相同点?有什么不同点?
3.填一填:完成下表
相同点 不同点
正比例
反比例
1.两个相关联的量
2.一个量变化 ,另一个量跟着变化
比值一定
乘积一定
一个量变大,另一个量跟着变大
一个量变大,另一个量反而变小
图像为一条直线
图像为一条曲线
=k(一定)
xy=k(一定)
1.判断下列相关联的两种量是不是成比例,成什么比例,并说明理由。
①给一块地板铺地砖,砖块的面积和块数。
②周长一定,圆的直径与圆周率。
③书的总页数一定,已看页数和未看页数。
④出油率一定,大豆油的质量与大豆的质量。
⑤一个自然数与它的倒数
砖块面积×块数=地板面积(一定)
反
直径×圆周率=周长(一定)
×
已看页数+未看页数=总页数(一定)
×
大豆油质量÷大豆质量=出油率(一定)
正
自然数×它的倒数=1(一定)
反
一定
有x、y、k三个相关的量,并有xy=k。
(1)当k一定时,x与y成________比例关系;
(2)当x一定时,k与y成________比例关系;
(3)当y一定时,k与x成________比例关系。
反
正
正
在生活中,x、y、k可以表示什么?请举出正、反比例的例子。
单价×数量=总价(一定)
底×高=平行四边形的面积(一定)
速度×时间=路程(一定)
长×宽=长方形的面积(一定)
xy=k(一定)
1.找 2.算 3.辨
……
你有什么收获?
还有什么疑问?
同学们,再见!
反比例
年 级:六年级
学 科:小学数学(北师大版)
第四单元
第5课时
反比例
想一想:怎样的两个量成正比例?
1.两个相关联的量;
2.一个量变化,另一个量也随着变化;
3.两个量中相对应的两个数的比值一定;
4. (一定);
反比例
猜一猜:怎样的两个量成反比例?
1.两个相关联的量
2.一个量变化,另一个量跟着变化
3.两个量的乘积一定
?
学习活动任务一:两个量的变化规律
①填一填:自学课本46页,并把表1、表2补充完整。
③比一比:他们之间的变化规律相同吗?有什么异同点?
②说一说:仔细观察,你发现了什么?
用x、у表示长方形相邻两边的边长,表1是面积为24cm2
的长方形相邻两边边长的变化关系(单位:cm)
表1
8
6
5
4.8
6
4
8
3
10
2.4
长方形一条边的长随着邻边长的增加而减少。
变长
变短
1×24=24 2×12=24
3×8=24 4×6=24 5×4.8=24 ……
乘积不变
× 2
÷2
×3
÷3
×几
÷几
面积为24cm2
用x、у表示长方形相邻两边的边长,表2是周长为24cm
的长方形相邻两边边长的变化关系(单位:cm)
表2
长方形一条边的长随着邻边长的增加而减少。
变长
变短
1+11=12 2+10=12
3+9=12 4+8=12 5+7=12 ……
和不变
+1
-1
+2
-2
+几
-几
周长为24cm
9
8
5
7
6
6
7
5
8
4
用x、у表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表1
表2
9
8
5
7
6
6
7
5
8
4
8
6
5
4.8
6
4
8
3
10
2.4
两个相关联的量
一个量变化,另一个量跟着变化。
乘积一定
和一定
时间/时 1 2 3 4 5 6 …
平均速度/ (千米/时) 300 150 100 75 60 50 …
当路程为300千米时,平均速度和时间的变化如下表:
速度×时间=路程(一定)
×2
÷2
×3
÷3
×几
÷几
变长
变慢
二、自主学习,构建新知
时间/时 1 2 3 4 5 6 …
平均速度/ (千米/时) 300 150 100 75 60 50 …
当路程为300千米时,平均速度和时间的变化如下表:
小结
像这样,两种相关联的量,一个量变化,另一个量也随着变化,而且这两个量中相对应的两个数的乘积一定,我们就说这两个量成反比例。
表1
8
6
5
4.8
6
4
8
3
10
2.4
速度×时间=路程(一定)
速度和时间成反比例
长×宽=长方形的面积(一定)
长和宽成反比例
用x、у表示长方形相邻两边的边长,表1是面积为24cm2的长方形相邻两边边长的变化关系,表2是周长为24cm的长方形相邻两边边长的变化关系。请把表格填写完整,并说说你分别发现了什么。(单位:cm)
表2
9
8
5
7
6
6
7
5
8
4
表2中的长方形相邻两边的长成反比例吗?为什么?
表1
8
6
5
4.8
6
4
8
3
10
2.4
乘积一定
和一定
表2不成反比例
速度×时间=路程(一定)
路程一定,速度和时间成反比例。
时间一定或速度一定
成什么比例呢?
路程÷速度=时间,时间一定,路程和速度成正比例。
路程÷时间=速度,速度一定,路程和时间成正比例。
300:1=300 600:2=300 900:3=300 ……
100:50=2 200:100=2 300:150=2 ……
速度×时间=路程,路程一定,速度和时间成反比例。
反比例
正比例
1×300=300
2×150=300
……
300÷1=300
600÷2=300
……
100÷50=2
200÷100=2
……
相同点 不同点
正比例
反比例
学习活动任务二:正、反比例异同点
1.想一想:他们的特征分别是什么?
2.比一比:他们有什么相同点?有什么不同点?
3.填一填:完成下表
相同点 不同点
正比例
反比例
1.两个相关联的量
2.一个量变化 ,另一个量跟着变化
比值一定
乘积一定
一个量变大,另一个量跟着变大
一个量变大,另一个量反而变小
图像为一条直线
图像为一条曲线
=k(一定)
xy=k(一定)
1.判断下列相关联的两种量是不是成比例,成什么比例,并说明理由。
①给一块地板铺地砖,砖块的面积和块数。
②周长一定,圆的直径与圆周率。
③书的总页数一定,已看页数和未看页数。
④出油率一定,大豆油的质量与大豆的质量。
⑤一个自然数与它的倒数
砖块面积×块数=地板面积(一定)
反
直径×圆周率=周长(一定)
×
已看页数+未看页数=总页数(一定)
×
大豆油质量÷大豆质量=出油率(一定)
正
自然数×它的倒数=1(一定)
反
一定
有x、y、k三个相关的量,并有xy=k。
(1)当k一定时,x与y成________比例关系;
(2)当x一定时,k与y成________比例关系;
(3)当y一定时,k与x成________比例关系。
反
正
正
在生活中,x、y、k可以表示什么?请举出正、反比例的例子。
单价×数量=总价(一定)
底×高=平行四边形的面积(一定)
速度×时间=路程(一定)
长×宽=长方形的面积(一定)
xy=k(一定)
1.找 2.算 3.辨
……
你有什么收获?
还有什么疑问?
同学们,再见!
