北师大版数学八年级上册第七章 平行线的证明 综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学八年级上册第七章 平行线的证明 综合素质评价(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 266.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览




文档简介
第七章 综合素质评价
一、选择题 (每题3分,共30分)
1.[母题教材P167习题T2 ]下列语句是命题的是( )
A.连接P,Q两点
B.画一条线段等于已知线段
C.过点M作直线PQ的垂线
D.两条直线相交,有且只有一个交点
2.下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )
A.5 B.2
C.4 D.8
3.如图,直线l1∥l2,且分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=50°,则∠2的度数是( )
(第3题)
A.130° B.100° C.90° D.70°
4.如图,能判定EB∥AC的条件是( )
(第4题)
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
5.下列命题中,不能作为公理的是( )
A.两点之间线段最短
B.两角及其夹边分别相等的两个三角形全等
C.全等三角形的面积相等
D.同位角相等,两直线平行
6.下列命题中,是真命题的为( )
A.三角形的一个外角大于任何一个内角
B.如果两个角相等,那么它们是对顶角
C.如果两个直角三角形的面积相等,那么它们全等
D.直角三角形的两锐角互余
7.如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是( )
(第7题)
A.20° B.80° C.60° D.40°
8. [情境题 生活应用]如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于( )
(第8题)
A.81° B.99° C.108° D.120°
9.如图,AD∥BC,BD为∠ABC的平分线,DE,DF分别是∠ADB和∠ADC的平分线,且∠BDF=α,则以下∠A与∠C的关系正确的是( )
A.∠A=∠C+α
B.∠A=∠C+2α
C.∠A=2∠C+α
D.∠A=2∠C+2α
10.如图①②③中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )
(第10题)
A.84° B.111° C.225° D.201°
二、填空题(每题3分,共15分)
11.“相等的两个角不互补”它是 命题(填“真”或“假”),改写成“ 如果……那么……”的形式为 .
12.[母题教材P185复习题T7 ]把一张对边互相平行的纸条折成如图所示的形状,EF是折痕,若∠EFB=30°,则∠AEG的度数为 .
13.[2024南宁兴宁区校级开学]如图,已知∠1+∠2=180°,∠3=112°,则∠4的度数为 .
(第13题)
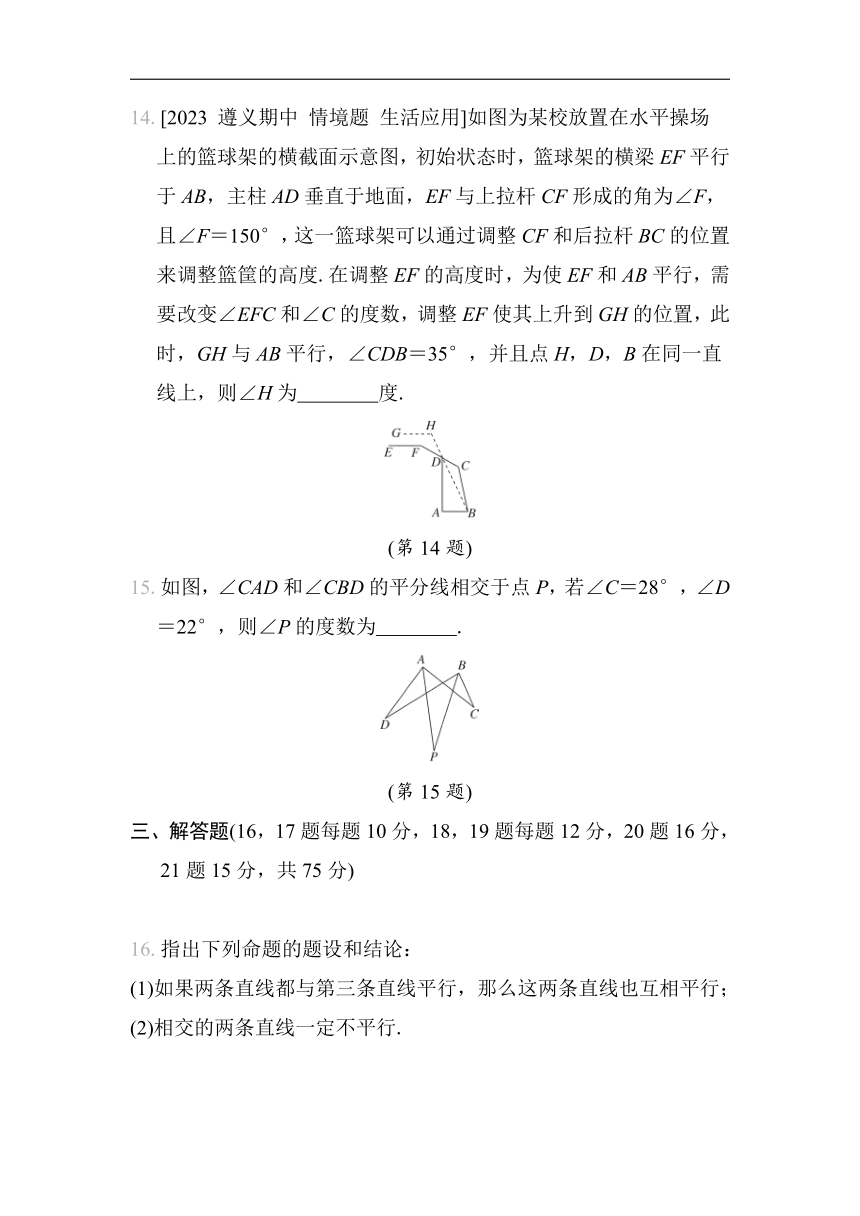
14.[2023 遵义期中 情境题 生活应用]如图为某校放置在水平操场上的篮球架的横截面示意图,初始状态时,篮球架的横梁EF平行于AB,主柱AD垂直于地面,EF与上拉杆CF形成的角为∠F,且∠F=150°,这一篮球架可以通过调整CF和后拉杆BC的位置来调整篮筐的高度.在调整EF的高度时,为使EF和AB平行,需要改变∠EFC和∠C的度数,调整EF使其上升到GH的位置,此时,GH与AB平行,∠CDB=35°,并且点H,D,B在同一直线上,则∠H为 度.
(第14题)
15.如图,∠CAD和∠CBD的平分线相交于点P,若∠C=28°,∠D=22°,则∠P的度数为 .
(第15题)
三、解答题(16,17题每题10分,18,19题每题12分,20题16分,21题15分,共75分)
16.指出下列命题的题设和结论:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)相交的两条直线一定不平行.
17.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A= ( ).
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( ).
∴DF∥ ( ).
∴∠EGF+∠AEG=180°( ).
18.如图,△ABC中,E是AB上一点,过D作DE∥BC交AB于点E,F是BC上一点,连接DF.若∠AED=∠1.
(1)求证:AB∥DF.
(2)若∠1=52°,DF平分∠CDE,求∠C的度数.
19.如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证:
(1)AB∥GD;
(2)∠3=∠B.
20.【问题背景】同学们,观察小猪的猪蹄,你会发现熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
【问题探究】(1)如图①,AB∥CD,E为AB,CD之间一点,连接AE,CE.可以得到∠AEC与∠A,∠C之间有怎样的数量关系,并说明理由;
【灵活应用】(2)如图②,直线AB∥CD,若∠E=∠B=60°,∠F=85°,求∠D的度数.
21. [新视角 新定义题]如图①,像我们常见的学习用品——圆规,我们把这样的图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠BAC,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
①如图②,把一块直角三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C,∠A=54°,则∠ABX+∠ACX= °;
②如图③,DC平分∠ADB,EC平分∠AEB,若∠DAE=α,∠DBE=β,请用含α和β的式子表示∠DCE的度数.
答案详解详析
一、1. D 2. B 3. B 4. A 5. C 6. D 7. D 8. B 9. B
10. D 【点拨】在题图①中,∠2+∠4=×(∠1+∠2+∠3+∠4)=×(180°-42°)=69°,故∠O1=180°-69°=111°;在题图②中,∠O2=∠4-∠2=[(∠3+∠4)-(∠1+∠2)]=∠A=21°;在题图③中,∠ABC+∠ACB=180°-∠A=180°-42°=138°,则∠1+∠2+∠3+∠4=180°+180°-138°=222°,故∠O3=180°-(∠2+∠3)=180°-×222°=69°,
∴∠O1+∠O2+∠O3=111°+21°+69°=201°.
二、11.假;如果两个角相等,那么这两个角不互补
12.120° 13.68° 14.115
15.25° 【点拨】设BD与AC交于点E,BP与AC交于点F,∵∠DEC是△ADE,△BCE的外角,∴∠D+∠DAE=∠C+∠CBE.又∵∠C=28°,∠D=22°,∴∠DAE-∠CBE=∠C-∠D=28°-22°=6°.∵AP是∠DAE的平分线,BP是∠CBE的平分线,∴∠DAP=∠PAE=∠DAE,∠CBP=∠PBE=∠CBE.∵在 △AFP,△BCF中,∠PFC是外角,∴∠PAF+∠P=∠CBF+∠C,即∠DAE+∠P=∠CBE+∠C.∴∠CBE-∠DAE+∠C=∠P.∴(∠CBE-∠DAE)+∠C=∠P,且∠DAE-∠CBE=6°.∴-(∠DAE-∠CBE)+∠C=-×6°+28°=25°.∴∠P的度数为25°.
三、16.【解】(1)题设是两条直线都与第三条直线平行,结论是这两条直线也互相平行;
(2)“相交的两条直线一定不平行”可改写为“如果两条直线相交,那么它们一定不平行”,故题设是两条直线相交,结论是它们一定不平行.
17.【解】∠CED;两直线平行,同位角相等;等量代换;AE;同位角相等,两直线平行;两直线平行,同旁内角互补
18.(1)【证明】∵DE∥BC,∴∠AED=∠B.
又∵∠1=∠AED,∴∠B=∠1.∴AB∥DF.
(2)【解】∵DE∥BC,∴∠EDF=∠1=52°.
∵DF平分∠CDE,∴∠CDF=∠EDF=52°.
在△CDF中,∵∠C+∠1+∠CDF=180°,
∴∠C=180°-∠1-∠CDF=180°-52°-52°=76°.
19.【证明】(1)∵AD⊥BC,EF⊥BC,
∴AD∥EF.∴∠1=∠EAD.
∵∠1=∠2,∴∠2=∠EAD,∴AB∥GD.
(2)∵AD⊥BC,EF⊥BC,
∴易得∠1+∠B=∠2+∠3=90°.
∵∠1=∠2,∴∠3=∠B.
20.【解】(1)∠AEC=∠A+∠C,理由如下:
点E作EF∥AB,如图,
∵AB∥CD,∴AB∥CD∥EF.
∴∠A=∠AEF,∠C=∠CEF.
∵∠AEC=∠AEF+∠CEF,
∴∠AEC=∠A+∠C.
(2)∵∠E=∠B=60°,∠F=85°,
∴∠BHF=180°-∠B-∠F=35°.
∴∠AHE=∠BHF=35°.
∴由“猪蹄模型”得∠D=∠DEH-∠AHE=25°.
21.【解】(1)∠BDC=∠BAC+∠B+∠C,理由如下:
如图,连接AD并延长到点E,
∵∠BDE是△ABD的外角,
∴∠BDE=∠B+∠BAD.
同理,∠CDE=∠C+∠CAD,
则∠BDE+∠CDE=∠BAD+∠CAD+∠B+∠C.
又∵∠BDE+∠CDE=∠BDC,∠BAD+∠CAD=∠BAC,∴∠BDC=∠BAC+∠B+∠C.
(2)①36
②由(1)中的结论可知,
∠DBE=∠CDB+∠DCE+∠CEB,
则∠CDB+∠CEB=∠DBE-∠DCE.
又∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠CDB,∠AEC=∠CEB.
∴∠ADC+∠AEC=∠CDB+∠CEB.
又∵∠DCE=∠ADC+∠DAE+∠AEC,
∴∠DCE=∠DBE-∠DCE+∠DAE.
即∠DCE=.
又∵∠DAE=α,∠DBE=β,
∴∠DCE=.
一、选择题 (每题3分,共30分)
1.[母题教材P167习题T2 ]下列语句是命题的是( )
A.连接P,Q两点
B.画一条线段等于已知线段
C.过点M作直线PQ的垂线
D.两条直线相交,有且只有一个交点
2.下列各数中,可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是( )
A.5 B.2
C.4 D.8
3.如图,直线l1∥l2,且分别与直线l交于点A,B,把一块含30°角的三角尺按如图所示的位置摆放.若∠1=50°,则∠2的度数是( )
(第3题)
A.130° B.100° C.90° D.70°
4.如图,能判定EB∥AC的条件是( )
(第4题)
A.∠A=∠ABE B.∠A=∠EBD
C.∠C=∠ABC D.∠C=∠ABE
5.下列命题中,不能作为公理的是( )
A.两点之间线段最短
B.两角及其夹边分别相等的两个三角形全等
C.全等三角形的面积相等
D.同位角相等,两直线平行
6.下列命题中,是真命题的为( )
A.三角形的一个外角大于任何一个内角
B.如果两个角相等,那么它们是对顶角
C.如果两个直角三角形的面积相等,那么它们全等
D.直角三角形的两锐角互余
7.如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是( )
(第7题)
A.20° B.80° C.60° D.40°
8. [情境题 生活应用]如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于( )
(第8题)
A.81° B.99° C.108° D.120°
9.如图,AD∥BC,BD为∠ABC的平分线,DE,DF分别是∠ADB和∠ADC的平分线,且∠BDF=α,则以下∠A与∠C的关系正确的是( )
A.∠A=∠C+α
B.∠A=∠C+2α
C.∠A=2∠C+α
D.∠A=2∠C+2α
10.如图①②③中,∠A=42°,∠1=∠2,∠3=∠4,则∠O1+∠O2+∠O3=( )
(第10题)
A.84° B.111° C.225° D.201°
二、填空题(每题3分,共15分)
11.“相等的两个角不互补”它是 命题(填“真”或“假”),改写成“ 如果……那么……”的形式为 .
12.[母题教材P185复习题T7 ]把一张对边互相平行的纸条折成如图所示的形状,EF是折痕,若∠EFB=30°,则∠AEG的度数为 .
13.[2024南宁兴宁区校级开学]如图,已知∠1+∠2=180°,∠3=112°,则∠4的度数为 .
(第13题)
14.[2023 遵义期中 情境题 生活应用]如图为某校放置在水平操场上的篮球架的横截面示意图,初始状态时,篮球架的横梁EF平行于AB,主柱AD垂直于地面,EF与上拉杆CF形成的角为∠F,且∠F=150°,这一篮球架可以通过调整CF和后拉杆BC的位置来调整篮筐的高度.在调整EF的高度时,为使EF和AB平行,需要改变∠EFC和∠C的度数,调整EF使其上升到GH的位置,此时,GH与AB平行,∠CDB=35°,并且点H,D,B在同一直线上,则∠H为 度.
(第14题)
15.如图,∠CAD和∠CBD的平分线相交于点P,若∠C=28°,∠D=22°,则∠P的度数为 .
(第15题)
三、解答题(16,17题每题10分,18,19题每题12分,20题16分,21题15分,共75分)
16.指出下列命题的题设和结论:
(1)如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
(2)相交的两条直线一定不平行.
17.完成下面的证明:
如图,点D,E,F分别是三角形ABC的边BC,CA,AB上的点,连接DE,DF,DE∥AB,∠BFD=∠CED,连接BE交DF于点G,求证:∠EGF+∠AEG=180°.
证明:∵DE∥AB(已知),
∴∠A= ( ).
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD( ).
∴DF∥ ( ).
∴∠EGF+∠AEG=180°( ).
18.如图,△ABC中,E是AB上一点,过D作DE∥BC交AB于点E,F是BC上一点,连接DF.若∠AED=∠1.
(1)求证:AB∥DF.
(2)若∠1=52°,DF平分∠CDE,求∠C的度数.
19.如图,已知:AD⊥BC,EF⊥BC,∠1=∠2.求证:
(1)AB∥GD;
(2)∠3=∠B.
20.【问题背景】同学们,观察小猪的猪蹄,你会发现熟悉的几何图形,我们就把这个图形的形象称为“猪蹄模型”,猪蹄模型中蕴含着角的数量关系.
【问题探究】(1)如图①,AB∥CD,E为AB,CD之间一点,连接AE,CE.可以得到∠AEC与∠A,∠C之间有怎样的数量关系,并说明理由;
【灵活应用】(2)如图②,直线AB∥CD,若∠E=∠B=60°,∠F=85°,求∠D的度数.
21. [新视角 新定义题]如图①,像我们常见的学习用品——圆规,我们把这样的图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠BAC,∠B,∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下两个问题:
①如图②,把一块直角三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY,XZ恰好经过点B,C,∠A=54°,则∠ABX+∠ACX= °;
②如图③,DC平分∠ADB,EC平分∠AEB,若∠DAE=α,∠DBE=β,请用含α和β的式子表示∠DCE的度数.
答案详解详析
一、1. D 2. B 3. B 4. A 5. C 6. D 7. D 8. B 9. B
10. D 【点拨】在题图①中,∠2+∠4=×(∠1+∠2+∠3+∠4)=×(180°-42°)=69°,故∠O1=180°-69°=111°;在题图②中,∠O2=∠4-∠2=[(∠3+∠4)-(∠1+∠2)]=∠A=21°;在题图③中,∠ABC+∠ACB=180°-∠A=180°-42°=138°,则∠1+∠2+∠3+∠4=180°+180°-138°=222°,故∠O3=180°-(∠2+∠3)=180°-×222°=69°,
∴∠O1+∠O2+∠O3=111°+21°+69°=201°.
二、11.假;如果两个角相等,那么这两个角不互补
12.120° 13.68° 14.115
15.25° 【点拨】设BD与AC交于点E,BP与AC交于点F,∵∠DEC是△ADE,△BCE的外角,∴∠D+∠DAE=∠C+∠CBE.又∵∠C=28°,∠D=22°,∴∠DAE-∠CBE=∠C-∠D=28°-22°=6°.∵AP是∠DAE的平分线,BP是∠CBE的平分线,∴∠DAP=∠PAE=∠DAE,∠CBP=∠PBE=∠CBE.∵在 △AFP,△BCF中,∠PFC是外角,∴∠PAF+∠P=∠CBF+∠C,即∠DAE+∠P=∠CBE+∠C.∴∠CBE-∠DAE+∠C=∠P.∴(∠CBE-∠DAE)+∠C=∠P,且∠DAE-∠CBE=6°.∴-(∠DAE-∠CBE)+∠C=-×6°+28°=25°.∴∠P的度数为25°.
三、16.【解】(1)题设是两条直线都与第三条直线平行,结论是这两条直线也互相平行;
(2)“相交的两条直线一定不平行”可改写为“如果两条直线相交,那么它们一定不平行”,故题设是两条直线相交,结论是它们一定不平行.
17.【解】∠CED;两直线平行,同位角相等;等量代换;AE;同位角相等,两直线平行;两直线平行,同旁内角互补
18.(1)【证明】∵DE∥BC,∴∠AED=∠B.
又∵∠1=∠AED,∴∠B=∠1.∴AB∥DF.
(2)【解】∵DE∥BC,∴∠EDF=∠1=52°.
∵DF平分∠CDE,∴∠CDF=∠EDF=52°.
在△CDF中,∵∠C+∠1+∠CDF=180°,
∴∠C=180°-∠1-∠CDF=180°-52°-52°=76°.
19.【证明】(1)∵AD⊥BC,EF⊥BC,
∴AD∥EF.∴∠1=∠EAD.
∵∠1=∠2,∴∠2=∠EAD,∴AB∥GD.
(2)∵AD⊥BC,EF⊥BC,
∴易得∠1+∠B=∠2+∠3=90°.
∵∠1=∠2,∴∠3=∠B.
20.【解】(1)∠AEC=∠A+∠C,理由如下:
点E作EF∥AB,如图,
∵AB∥CD,∴AB∥CD∥EF.
∴∠A=∠AEF,∠C=∠CEF.
∵∠AEC=∠AEF+∠CEF,
∴∠AEC=∠A+∠C.
(2)∵∠E=∠B=60°,∠F=85°,
∴∠BHF=180°-∠B-∠F=35°.
∴∠AHE=∠BHF=35°.
∴由“猪蹄模型”得∠D=∠DEH-∠AHE=25°.
21.【解】(1)∠BDC=∠BAC+∠B+∠C,理由如下:
如图,连接AD并延长到点E,
∵∠BDE是△ABD的外角,
∴∠BDE=∠B+∠BAD.
同理,∠CDE=∠C+∠CAD,
则∠BDE+∠CDE=∠BAD+∠CAD+∠B+∠C.
又∵∠BDE+∠CDE=∠BDC,∠BAD+∠CAD=∠BAC,∴∠BDC=∠BAC+∠B+∠C.
(2)①36
②由(1)中的结论可知,
∠DBE=∠CDB+∠DCE+∠CEB,
则∠CDB+∠CEB=∠DBE-∠DCE.
又∵DC平分∠ADB,EC平分∠AEB,
∴∠ADC=∠CDB,∠AEC=∠CEB.
∴∠ADC+∠AEC=∠CDB+∠CEB.
又∵∠DCE=∠ADC+∠DAE+∠AEC,
∴∠DCE=∠DBE-∠DCE+∠DAE.
即∠DCE=.
又∵∠DAE=α,∠DBE=β,
∴∠DCE=.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
