北师大版数学八年级上册第一章 勾股定理 综合素质评价(含答案)
文档属性
| 名称 | 北师大版数学八年级上册第一章 勾股定理 综合素质评价(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览


文档简介
第一章 综合素质评价
一、选择题(每题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,则AB的平方为( )
(第1题)
A.9 B.16 C.25 D.41
2.下列各组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.,,1
C.4,5,6 D.7,24,25
3.在△ABC中,∠B=35°,BC2-AC2=AB2,则∠C的大小为( )
A.35° B.55° C.65° D.90°
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD的长度是( )
(第4题)
A.2 B.3 C.4 D.5
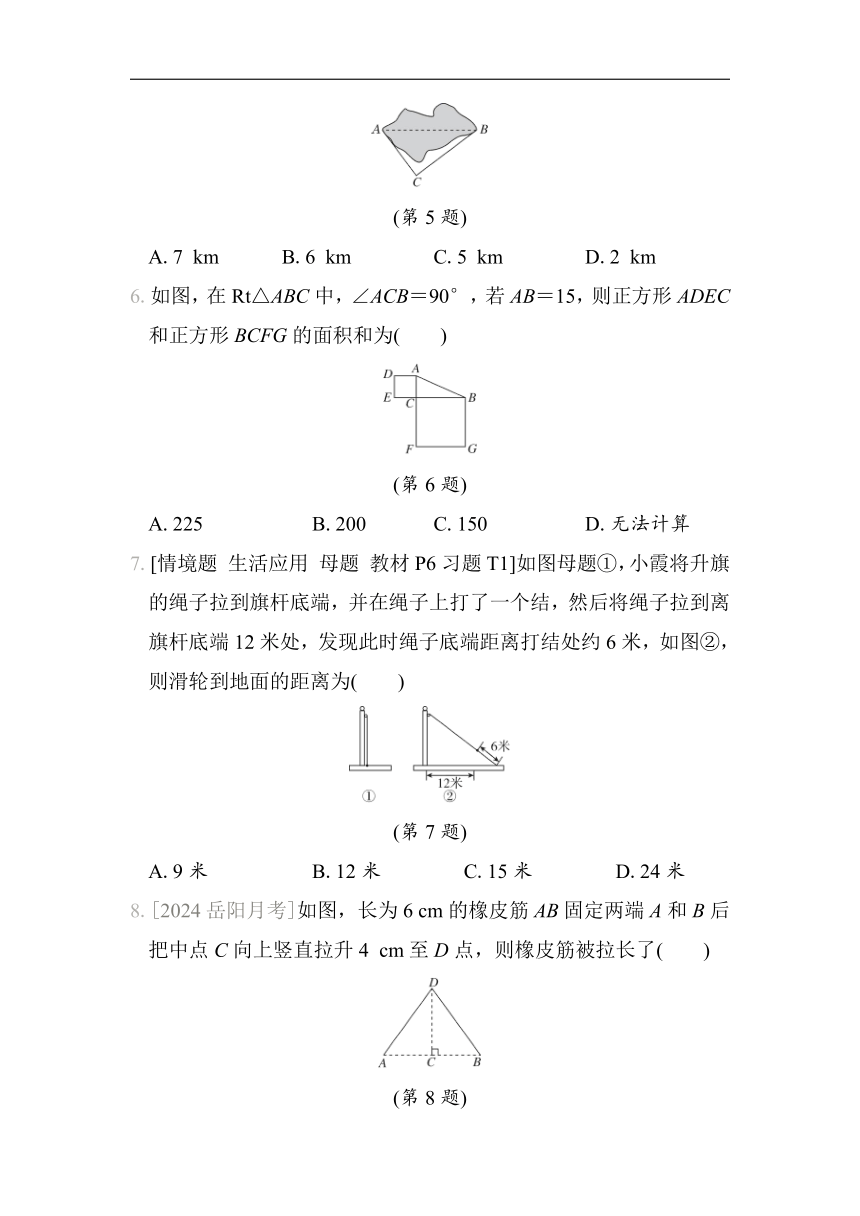
5.[情境题 生活应用]如图,在A村与B村之间有一座大山,原来从A村到B村,需沿道路A→C→B(∠C=90°)绕过村庄间的大山,打通A,B间的隧道后,就可直接从A村到B村.已知AC=9 km,BC=12 km,那么打通隧道后从A村到B村比原来减少的路程为( )
(第5题)
A.7 km B.6 km C.5 km D.2 km
6.如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
(第6题)
A.225 B.200 C.150 D.无法计算
7.[情境题 生活应用 母题 教材P6习题T1]如图母题①,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,如图②,则滑轮到地面的距离为( )
(第7题)
A.9米 B.12米 C.15米 D.24米
8.[2024岳阳月考]如图,长为6 cm的橡皮筋AB固定两端A和B后把中点C向上竖直拉升4 cm至D点,则橡皮筋被拉长了( )
(第8题)
A.2 cm B.3 cm C.4 cm D.5 cm
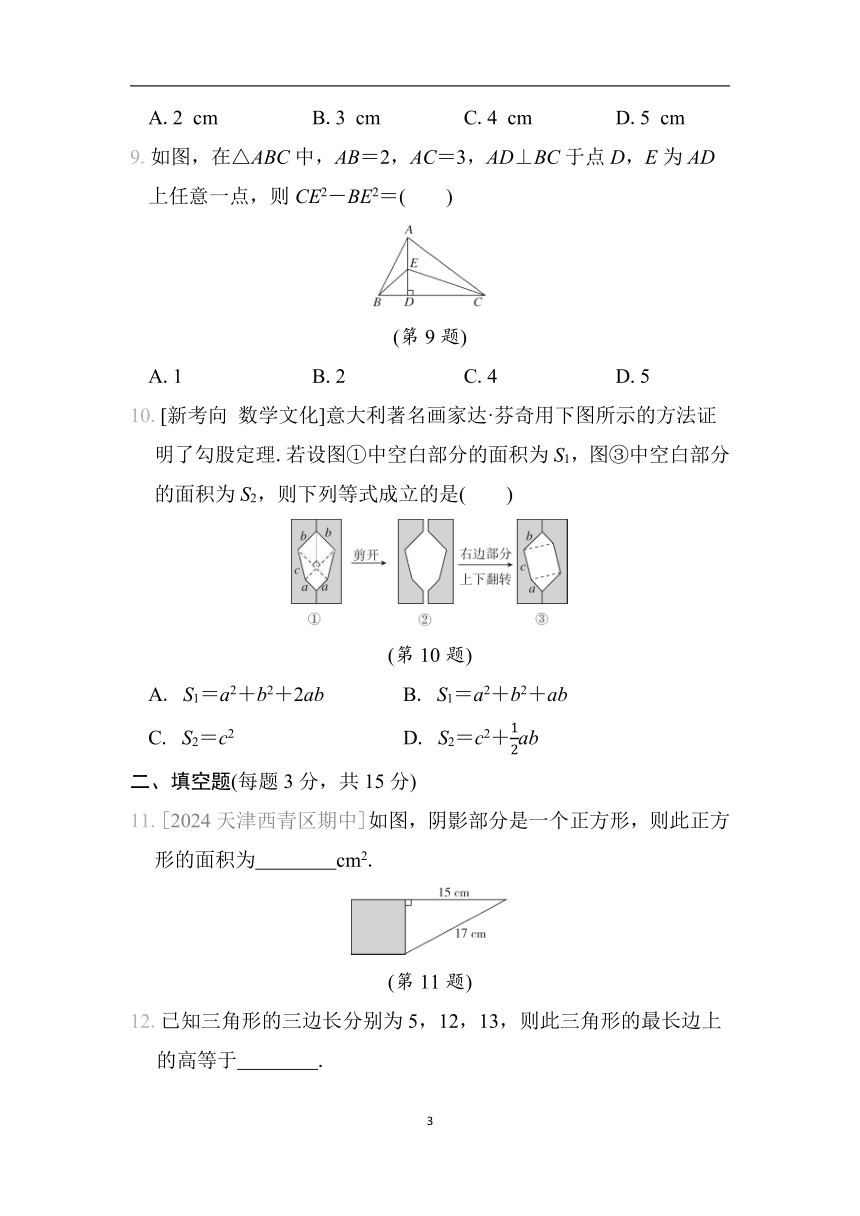
9.如图,在△ABC中,AB=2,AC=3,AD⊥BC于点D,E为AD上任意一点,则CE2-BE2=( )
(第9题)
A.1 B.2 C.4 D.5
10.[新考向 数学文化]意大利著名画家达·芬奇用下图所示的方法证明了勾股定理.若设图①中空白部分的面积为S1,图③中空白部分的面积为S2,则下列等式成立的是( )
(第10题)
A. S1=a2+b2+2ab B. S1=a2+b2+ab
C. S2=c2 D. S2=c2+ab
二、填空题(每题3分,共15分)
11.[2024天津西青区期中]如图,阴影部分是一个正方形,则此正方形的面积为 cm2.
(第11题)
12.已知三角形的三边长分别为5,12,13,则此三角形的最长边上的高等于 .
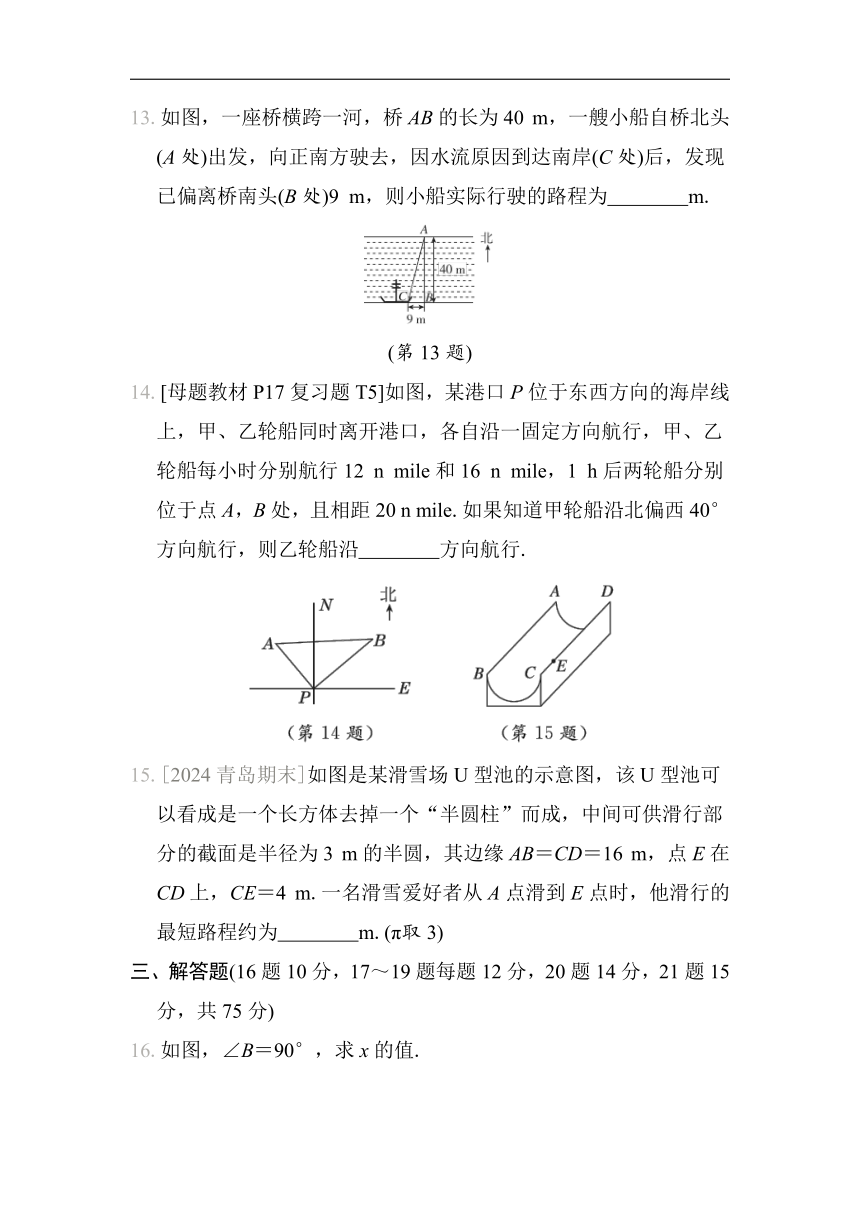
13.如图,一座桥横跨一河,桥AB的长为40 m,一艘小船自桥北头(A处)出发,向正南方驶去,因水流原因到达南岸(C处)后,发现已偏离桥南头(B处)9 m,则小船实际行驶的路程为 m.
(第13题)
14.[母题教材P17复习题T5]如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12 n mile和16 n mile,1 h后两轮船分别位于点A,B处,且相距20 n mile.如果知道甲轮船沿北偏西40°方向航行,则乙轮船沿 方向航行.
15.[2024青岛期末]如图是某滑雪场U型池的示意图,该U型池可以看成是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3 m的半圆,其边缘AB=CD=16 m,点E在CD上,CE=4 m.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 m.(π取3)
三、解答题(16题10分,17~19题每题12分,20题14分,21题15分,共75分)
16.如图,∠B=90°,求x的值.
17.如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.试说明△ACD是直角三角形.
18.[2024赣州期末]图①是放置在水平面上的可折叠式护眼灯,其中底座的高AB=5 cm,连杆BC=30 cm,灯罩CD=20 cm.如图②,转动BC,CD,使得∠BCD成平角,且灯罩端点D离桌面l的高度DH为45 cm,求AH的距离.
19.观察下列勾股数:
①3,4,5,且32=4+5;
②5,12,13,且52=12+13;
③7,24,25,且72=24+25;
④9,b,c,且92=b+c;
…
(1)请你根据上述规律,并结合相关知识求:b= ,c= ;
(2)猜想第n组勾股数,并说明你的猜想正确.
20.如图①,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 ;
A B C D
(2)求该长度最短的金属丝的长;
(3)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝的最短长度为m,则m2的值为 .
21.“赵爽弦图”是四个全等的直角三角形与一个小正方形拼成的大正方形.赵爽利用几何图形的截、割、拼、补来证明代数式之间的恒等关系,验证勾股定理,为中国古代以形证数、形数统一,代数和几何紧密结合、互不可分的独特风格树立了一个典范.
(1)如图①,是小琪制作的一个“赵爽弦图”纸板.
①设AH=a,BH=b,AB=c,请你利用图①验证a2+b2=c2;
②若大正方形ABCD的边长为13,小正方形EFGH的边长为7,求直角三角形两直角边之和为多少.
(2)如图②,小昊把四个全等的直角三角板紧密地拼接在一起,已知外围轮廓(实线)的周长为48,OB=6,求这个图案的面积.
答案详解详析
一、1. D 2. D 3. B 4. A 5. B 6. A 7. A 8. C
9. D 【点拨】在Rt△ABD和Rt△ADC中,
BD2=AB2-AD2,CD2=AC2-AD2,
所以在Rt△BDE和Rt△CDE中,
BE2=BD2+ED2=AB2-AD2+ED2,EC2=CD2+ED2=AC2-AD2+ED2,
所以EC2-EB2=(AC2-AD2+ED2)-(AB2-AD2+ED2)=AC2-AB2=32-22=5.
10. B
二、11.64 12. 13.41
14.北偏东50°(或东偏北40°) 【点拨】因为AP=1×12=12(n mile),PB=1×16=16(n mile),AB=20 n mile,所以AP2+BP2=400=AB2,所以∠APB=90°.因为∠APN=40°,所以∠BPN=50°.因为∠EPN=90°,所以∠BPE=40°.所以乙轮船沿北偏东50°(或东偏北40°)方向航行.
15.15 【点拨】如图是U型池的内侧面展开图,
则AD≈3×3=9(m),CD=16 m,CE=4 m.所以DE=CD-CE=16-4=12(m).
在Rt△ADE中,AE2=AD2+DE2≈92+122=152,所以AE≈15 m.故他滑行的最短路程约为15 m.
三、16.【解】由勾股定理,得62+x2=(x+4)2,
解得x=2.5.故x的值为2.5.
17.【解】因为AB=15,BC=9,∠ACB=90°,
所以AC2=152-92=144.
因为52+144=132,所以AD2+AC2=CD2,
所以∠DAC=90°,所以△ACD是直角三角形.
18.【解】由题意,得BD=BC+CD=50 cm.
如图,过点B作BE⊥DH于点E,
易得EH=AB=5 cm,BE=AH,
所以DE=DH-EH=40 cm,
所以BE2=BD2-DE2=302.
所以BE=30 cm,所以AH=30 cm.
19.【解】(1)40;41
(2)猜想第n组勾股数为2n+1,2n2+2n,2n2+2n+1.
因为(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1,(2n2+2n+1)2=4n4+8n3+8n2+4n+1,
所以(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
因为n是正整数,
所以2n+1,2n2+2n,2n2+2n+1是一组勾股数.
20.【解】(1)A
(2)由(1)可知该长度最短的金属丝的长为2AC.
因为圆柱底面的周长为12,
所以BC=×12=6.
因为圆柱的高AB=8,
所以AC2=62+82=100,所以AC=10,所以该长度最短的金属丝的长为2AC=2×10=20.
(3)2 368 【点拨】若将金属丝从点B绕四圈到达点A,则m2=42×=2 368.
21.【解】(1)①设题图①中大、小两个正方形的面积分别为S1和S2,则S2=(b-a)2=a2+b2-2ab,S1=S2+4×ab=a2+b2.
又因为S1=c2,所以a2+b2=c2.
②因为AB=13,EF=7,
所以大正方形的面积是169,小正方形的面积是49,
所以四个直角三角形的面积和为169-49=120,设AE为x,DE为y,则4×xy=2xy=120,
易知x2+y2=132=169,
所以(x+y)2=x2+y2+2xy=169+120=289,
所以x+y=17,
所以直角三角形两直角边之和为17.
(2)由题意,得AB+BC=48÷4=12,OH=OB=6.
设AH=BC=x,则AB=12-x,OA=6+x,
在Rt△AOB中,由勾股定理,得OB2+OA2=AB2,即62+(6+x)2=(12-x)2,
解得x=2,所以OA=OH+AH=6+2=8,
所以该图形的面积为4×OB·OA=2OB·OA=2×6×8=96.
一、选择题(每题3分,共30分)
1.如图,在Rt△ABC中,∠C=90°,AC=4,BC=5,则AB的平方为( )
(第1题)
A.9 B.16 C.25 D.41
2.下列各组数中,是勾股数的是( )
A.0.3,0.4,0.5 B.,,1
C.4,5,6 D.7,24,25
3.在△ABC中,∠B=35°,BC2-AC2=AB2,则∠C的大小为( )
A.35° B.55° C.65° D.90°
4.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点A为圆心,AC长为半径画弧,交AB于点D,则BD的长度是( )
(第4题)
A.2 B.3 C.4 D.5
5.[情境题 生活应用]如图,在A村与B村之间有一座大山,原来从A村到B村,需沿道路A→C→B(∠C=90°)绕过村庄间的大山,打通A,B间的隧道后,就可直接从A村到B村.已知AC=9 km,BC=12 km,那么打通隧道后从A村到B村比原来减少的路程为( )
(第5题)
A.7 km B.6 km C.5 km D.2 km
6.如图,在Rt△ABC中,∠ACB=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
(第6题)
A.225 B.200 C.150 D.无法计算
7.[情境题 生活应用 母题 教材P6习题T1]如图母题①,小霞将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端12米处,发现此时绳子底端距离打结处约6米,如图②,则滑轮到地面的距离为( )
(第7题)
A.9米 B.12米 C.15米 D.24米
8.[2024岳阳月考]如图,长为6 cm的橡皮筋AB固定两端A和B后把中点C向上竖直拉升4 cm至D点,则橡皮筋被拉长了( )
(第8题)
A.2 cm B.3 cm C.4 cm D.5 cm
9.如图,在△ABC中,AB=2,AC=3,AD⊥BC于点D,E为AD上任意一点,则CE2-BE2=( )
(第9题)
A.1 B.2 C.4 D.5
10.[新考向 数学文化]意大利著名画家达·芬奇用下图所示的方法证明了勾股定理.若设图①中空白部分的面积为S1,图③中空白部分的面积为S2,则下列等式成立的是( )
(第10题)
A. S1=a2+b2+2ab B. S1=a2+b2+ab
C. S2=c2 D. S2=c2+ab
二、填空题(每题3分,共15分)
11.[2024天津西青区期中]如图,阴影部分是一个正方形,则此正方形的面积为 cm2.
(第11题)
12.已知三角形的三边长分别为5,12,13,则此三角形的最长边上的高等于 .
13.如图,一座桥横跨一河,桥AB的长为40 m,一艘小船自桥北头(A处)出发,向正南方驶去,因水流原因到达南岸(C处)后,发现已偏离桥南头(B处)9 m,则小船实际行驶的路程为 m.
(第13题)
14.[母题教材P17复习题T5]如图,某港口P位于东西方向的海岸线上,甲、乙轮船同时离开港口,各自沿一固定方向航行,甲、乙轮船每小时分别航行12 n mile和16 n mile,1 h后两轮船分别位于点A,B处,且相距20 n mile.如果知道甲轮船沿北偏西40°方向航行,则乙轮船沿 方向航行.
15.[2024青岛期末]如图是某滑雪场U型池的示意图,该U型池可以看成是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为3 m的半圆,其边缘AB=CD=16 m,点E在CD上,CE=4 m.一名滑雪爱好者从A点滑到E点时,他滑行的最短路程约为 m.(π取3)
三、解答题(16题10分,17~19题每题12分,20题14分,21题15分,共75分)
16.如图,∠B=90°,求x的值.
17.如图,四边形ABCD中,∠ACB=90°,AB=15,BC=9,AD=5,DC=13.试说明△ACD是直角三角形.
18.[2024赣州期末]图①是放置在水平面上的可折叠式护眼灯,其中底座的高AB=5 cm,连杆BC=30 cm,灯罩CD=20 cm.如图②,转动BC,CD,使得∠BCD成平角,且灯罩端点D离桌面l的高度DH为45 cm,求AH的距离.
19.观察下列勾股数:
①3,4,5,且32=4+5;
②5,12,13,且52=12+13;
③7,24,25,且72=24+25;
④9,b,c,且92=b+c;
…
(1)请你根据上述规律,并结合相关知识求:b= ,c= ;
(2)猜想第n组勾股数,并说明你的猜想正确.
20.如图①,已知圆柱底面的周长为12,圆柱的高为8,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.
(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 ;
A B C D
(2)求该长度最短的金属丝的长;
(3)如图②,若将金属丝从点B绕四圈到达点A,则所需金属丝的最短长度为m,则m2的值为 .
21.“赵爽弦图”是四个全等的直角三角形与一个小正方形拼成的大正方形.赵爽利用几何图形的截、割、拼、补来证明代数式之间的恒等关系,验证勾股定理,为中国古代以形证数、形数统一,代数和几何紧密结合、互不可分的独特风格树立了一个典范.
(1)如图①,是小琪制作的一个“赵爽弦图”纸板.
①设AH=a,BH=b,AB=c,请你利用图①验证a2+b2=c2;
②若大正方形ABCD的边长为13,小正方形EFGH的边长为7,求直角三角形两直角边之和为多少.
(2)如图②,小昊把四个全等的直角三角板紧密地拼接在一起,已知外围轮廓(实线)的周长为48,OB=6,求这个图案的面积.
答案详解详析
一、1. D 2. D 3. B 4. A 5. B 6. A 7. A 8. C
9. D 【点拨】在Rt△ABD和Rt△ADC中,
BD2=AB2-AD2,CD2=AC2-AD2,
所以在Rt△BDE和Rt△CDE中,
BE2=BD2+ED2=AB2-AD2+ED2,EC2=CD2+ED2=AC2-AD2+ED2,
所以EC2-EB2=(AC2-AD2+ED2)-(AB2-AD2+ED2)=AC2-AB2=32-22=5.
10. B
二、11.64 12. 13.41
14.北偏东50°(或东偏北40°) 【点拨】因为AP=1×12=12(n mile),PB=1×16=16(n mile),AB=20 n mile,所以AP2+BP2=400=AB2,所以∠APB=90°.因为∠APN=40°,所以∠BPN=50°.因为∠EPN=90°,所以∠BPE=40°.所以乙轮船沿北偏东50°(或东偏北40°)方向航行.
15.15 【点拨】如图是U型池的内侧面展开图,
则AD≈3×3=9(m),CD=16 m,CE=4 m.所以DE=CD-CE=16-4=12(m).
在Rt△ADE中,AE2=AD2+DE2≈92+122=152,所以AE≈15 m.故他滑行的最短路程约为15 m.
三、16.【解】由勾股定理,得62+x2=(x+4)2,
解得x=2.5.故x的值为2.5.
17.【解】因为AB=15,BC=9,∠ACB=90°,
所以AC2=152-92=144.
因为52+144=132,所以AD2+AC2=CD2,
所以∠DAC=90°,所以△ACD是直角三角形.
18.【解】由题意,得BD=BC+CD=50 cm.
如图,过点B作BE⊥DH于点E,
易得EH=AB=5 cm,BE=AH,
所以DE=DH-EH=40 cm,
所以BE2=BD2-DE2=302.
所以BE=30 cm,所以AH=30 cm.
19.【解】(1)40;41
(2)猜想第n组勾股数为2n+1,2n2+2n,2n2+2n+1.
因为(2n+1)2+(2n2+2n)2=4n4+8n3+8n2+4n+1,(2n2+2n+1)2=4n4+8n3+8n2+4n+1,
所以(2n+1)2+(2n2+2n)2=(2n2+2n+1)2.
因为n是正整数,
所以2n+1,2n2+2n,2n2+2n+1是一组勾股数.
20.【解】(1)A
(2)由(1)可知该长度最短的金属丝的长为2AC.
因为圆柱底面的周长为12,
所以BC=×12=6.
因为圆柱的高AB=8,
所以AC2=62+82=100,所以AC=10,所以该长度最短的金属丝的长为2AC=2×10=20.
(3)2 368 【点拨】若将金属丝从点B绕四圈到达点A,则m2=42×=2 368.
21.【解】(1)①设题图①中大、小两个正方形的面积分别为S1和S2,则S2=(b-a)2=a2+b2-2ab,S1=S2+4×ab=a2+b2.
又因为S1=c2,所以a2+b2=c2.
②因为AB=13,EF=7,
所以大正方形的面积是169,小正方形的面积是49,
所以四个直角三角形的面积和为169-49=120,设AE为x,DE为y,则4×xy=2xy=120,
易知x2+y2=132=169,
所以(x+y)2=x2+y2+2xy=169+120=289,
所以x+y=17,
所以直角三角形两直角边之和为17.
(2)由题意,得AB+BC=48÷4=12,OH=OB=6.
设AH=BC=x,则AB=12-x,OA=6+x,
在Rt△AOB中,由勾股定理,得OB2+OA2=AB2,即62+(6+x)2=(12-x)2,
解得x=2,所以OA=OH+AH=6+2=8,
所以该图形的面积为4×OB·OA=2OB·OA=2×6×8=96.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
