2023-2024学年江苏省南通市海安实验中学高一(下)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年江苏省南通市海安实验中学高一(下)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 55.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 11:12:29 | ||
图片预览




文档简介
2023-2024学年江苏省南通市海安实验中学高一(下)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若向量,则( )
A. B. C. D.
2.已知复数是纯虚数,则实数的值为( )
A. B. 或 C. D.
3.已知的内角,,所对的边分别是,,,若,,则的值为( )
A. B. C. D.
4.设、是方程的两个根,则( )
A. B. C. D.
5.若是平面内的一组基底,则下列四组向量中能作为平面向量的基底的是( )
A. B.
C. D.
6.已知向量,,则在上的投影向量为( )
A. B. C. D.
7.在,其内角,,的对边分别为,,,若,则的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
8.在中,厘米,厘米,若利用正弦定理解有两解,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.对于任意的平面向量,,,下列说法错误的是( )
A. 若且,则
B.
C. 若,且,则
D.
10.已知,,下列命题正确的是( )
A.
B.
C. 若,则,至少有个为
D. 若,是两个虚数,,,则,为共轭复数
11.已知的内角,,所对的边分别为,,,则下列命题正确的是( )
A. 若,则一定为等腰三角形
B. 若,则
C. 若::::,则的最大内角为
D. 若为锐角三角形,则
三、填空题:本题共3小题,每小题5分,共15分。
12.若在中,,,,则 ______.
13.的最大值为______.
14.已知复数在复平面内对应的点为,且满足,为原点,,求的取值范围______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
求值:
;
;
.
16.本小题分
如图,在平面四边形中,,,的面积为.
求的长;
若,,求的长.
17.本小题分
已知复数在复平面内对应的点在虚轴的正半轴上,复数.
求,的值;
求,的值.
18.本小题分
如图在中,,,设,.
用表示向量.
若,,,求.
若,,求.
19.本小题分
某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角和以为直径的半圆拼接而成,点为半圆上一点异于,,点在线段上,且满足已知,,设.
为了使工艺礼品达到最佳观赏效果,需满足,且达到最大当为何值时,工艺礼品达到最佳观赏效果?
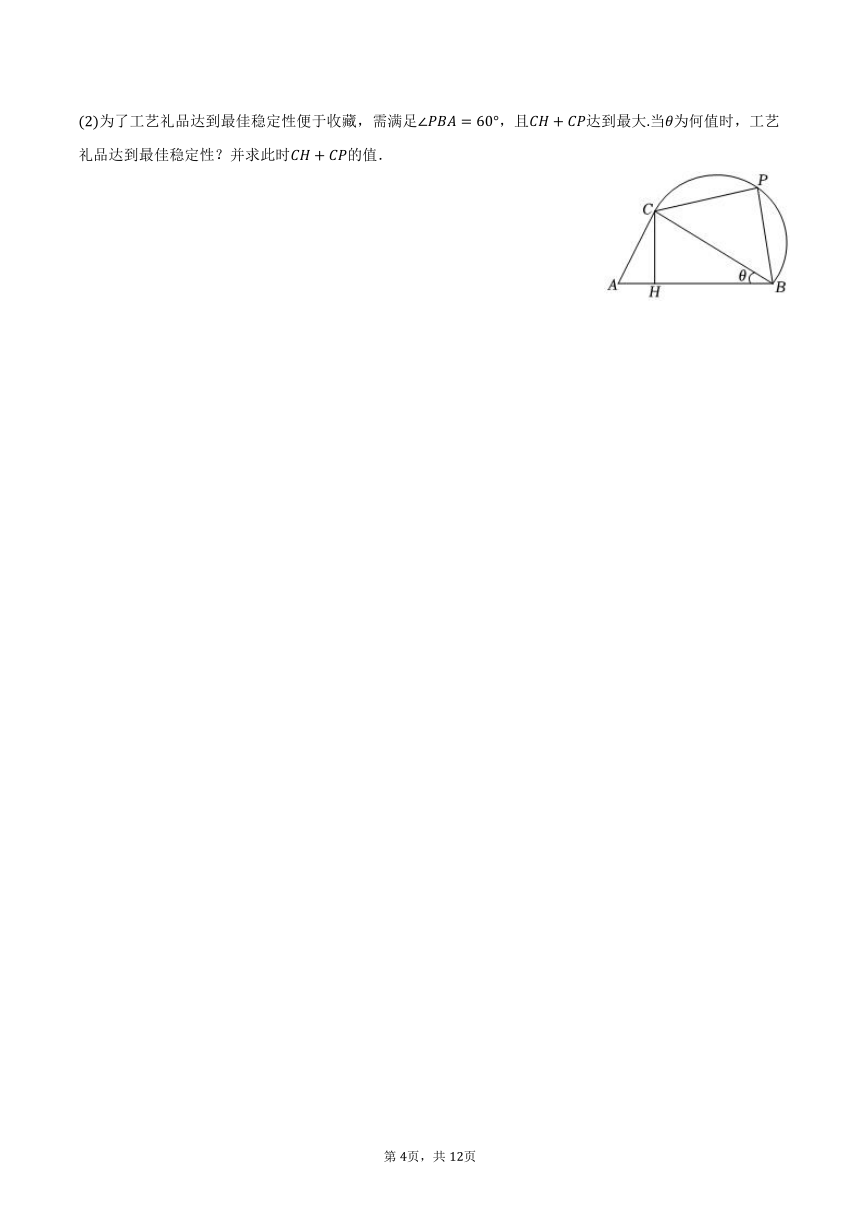
为了工艺礼品达到最佳稳定性便于收藏,需满足,且达到最大当为何值时,工艺礼品达到最佳稳定性?并求此时的值.
答案和解析
1.【答案】
【解析】解:由题意,,解得.
故选:.
根据向量共线的坐标公式求解.
本题考查平面向量的应用,属于基础题.
2.【答案】
【解析】解:根据题意,复数是纯虚数,
则有且,则.
故选:.
根据题意,由纯虚数的定义可得关于的方程,解可得答案.
本题考查纯虚数的定义,注意复数的分类,属于基础题.
3.【答案】
【解析】解:因为,,
由正弦定理,可得,,
则.
故选:.
由已知利用正弦定理即可求解.
本题考查了正弦定理在解三角形中的应用,属于基础题.
4.【答案】
【解析】【分析】
此题考查了两角和与差的正切函数公式,以及根与系数的关系,属于基础题.
根据题意易得,,代入求解即可.
【解答】
解:,是方程的两个根,
,,
则.
故选:.
5.【答案】
【解析】解:因为与共线,不符合题意;
假设,则与共线,不符合题意;
,即与共线,不符合题意;
不存在实数,使得,即与不共线,符合题意.
故选:.
结合向量的共线定理及平面向量基本定理检验各选项即可判断.
本题主要考查了向量共线定理的应用,还考查了平面向量基本定理的应用,属于基础题.
6.【答案】
【解析】解:,,
,,
则在上的投影向量为:.
故选:.
根据已知条件,结合投影向量的公式,即可求解.
本题主要考查投影向量的公式,属于基础题.
7.【答案】
【解析】解:,
由余弦定理可得:,整理可得:,
,则的形状为等腰三角形.
故选:.
由余弦定理化简已知等式可求,即可得解三角形的形状.
本题主要考查了余弦定理在解三角形中的应用,熟练掌握余弦定理是解题的关键,属于基础题.
8.【答案】
【解析】解:如图,
,,则,
以为圆心,为半径画圆弧,要使有两个解,则圆弧和边应该有两个交点,
故CA且,即,
解得.
故选:.
以为圆心,为半径画圆弧,圆弧与边应该有两个交点,此时三角形有两解,数形结合即可求出的范围.
本题考查了数形结合的应用,属于基础题.
9.【答案】
【解析】解:且,当为零向量时,则与不一定共线,即A错误,
由向量乘法的分配律可得:,即B正确,
因为,则,又,则或,即C错误,
取为非零向量,且与垂直,与不垂直,则,,即D错误,
故选:.
平面向量共线的传递性可得A错误,由向量乘法的分配律可得B正确,由向量垂直的运算可得,D错误,得解.
本题考查了平面向量共线的传递性、向量乘法的分配律,向量垂直的运算,属基础题.
10.【答案】
【解析】解:当时,显然错误;
设,都是实数,
则,
所以,
,B正确;
若,则
故,至少有个为,C正确;
设,都是实数,则,
,
若,,则,
所以,,即,为共轭复数,D正确.
故选:.
由已知结合复数的四则运算及复数的基本概念检验各选项即可判断.
本题主要考查了复数的四则运算及复数的基本概念,属于中档题.
11.【答案】
【解析】解:对于,由和正弦定理得:,故A正确;
对于,由及余弦函数在单调递减,得,故B错误;
对于,由::::及大边对大角得,角最大,设,,,
则,,故C正确;
对于,由为锐角三角形得,,又正弦函数在单调递增,
,即,故D正确.
故选:.
根据三角形的基本性质及正、余弦定理,正余弦函数的单调性,逐项分析即可.
本题考查正、余弦定理,三角函数的性质和推理能力,属中档题.
12.【答案】
【解析】解:由余弦定理,得,
所以.
故答案为:.
根据题意,利用数量积的定义和余弦定理加以计算,可得的值.
本题主要考查余弦定理、平面向量的数量积的定义等知识,考查了计算能力,属于基础题.
13.【答案】
【解析】解:,
即函数的最大值为,当,即,时取等号.
故答案为:.
先结合二倍角公式进行化简,然后结合正弦函数的性质即可求解.
本题主要考查了正弦函数最值的求解,属于基础题.
14.【答案】
【解析】解:设,则,
设复平面内一点,
则有,
即点在以点为圆心,为半径的圆周上或圆内,
设直线与圆交于,两点,
则,,而,表示在上的投影,
由图可知,,,
则,,
又因为,,,
所以,
即,
所以的取值范围为
故答案为:
设,则,由复数的几何意义可知,点在以点为圆心,为半径的圆周上或圆内,再结合平面向量数量积的几何意义求解.
本题主要考查了复数的几何意义,考查了平面向量的数量积运算,属于中档题.
15.【答案】解:根据题意,;
;
【解析】由虚数单位的性质计算可得答案;
由复数的乘法公式计算可得答案;
由复数的除法公式计算可得答案.
本题考查复数的计算,注意复数的四则运算法则,属于基础题.
16.【答案】解:,,的面积为,
,
,
由余弦定理,得
,
;
由知中,,,
,,,
又,,
在中,由正弦定理,得,
即,.
【解析】根据,求出,再利用余弦定理得;
根据已知条件在中,求出,再利用正弦定理求出.
本题考查了正弦定理,余弦定理和面积公式的应用,熟练掌握正余弦定理和面积公式是解本题的关键,属基础题.
17.【答案】解:由在复平面内对应的点在虚轴的正半轴上,
可得,
又复数,
可得,
即,;
由可知,,
所以,
.
【解析】根据复数的几何意义及同角三角函数关系计算即可;
利用三角恒等变换计算即可.
本题主要考查了复数的几何意义,和差角公式,同角基本关系在三角化简求值中的应用,属于中档题.
18.【答案】解:由题意有:
;
;
由题意,,,,
则;
,由,,
可得,即,
解得,,
故.
【解析】由平面向量的线性运算即可求解;
由向量的模长公式代入数据求解;
由向量垂直的性质可得,,再根据夹角公式即可求得.
本题考查平面向量的线性运算及数量积运算,属中档题.
19.【答案】解:由题意可得,
因为,
在直角中,可得,,
在直角中,可得,,
可得
,
所以当,即时,的最大值为,
即时,工艺礼品达到最佳观赏效果;
在直角中,由,
因为,,,
可得,
因为,
所以在直角中,,
所以,,
所以
,
可得当时,工艺礼品达到最佳稳定性,此时取得最大值,且最大值为.
【解析】利用直角三角形的边角关系,求出的解析式,从而可得取得最大值时的值;
由等积法求出的值,再计算的最大值以及对应的值.
本题考查了解三角形以及三角函数的应用问题,也考查了运算求解能力,是中档题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若向量,则( )
A. B. C. D.
2.已知复数是纯虚数,则实数的值为( )
A. B. 或 C. D.
3.已知的内角,,所对的边分别是,,,若,,则的值为( )
A. B. C. D.
4.设、是方程的两个根,则( )
A. B. C. D.
5.若是平面内的一组基底,则下列四组向量中能作为平面向量的基底的是( )
A. B.
C. D.
6.已知向量,,则在上的投影向量为( )
A. B. C. D.
7.在,其内角,,的对边分别为,,,若,则的形状是( )
A. 等腰三角形 B. 直角三角形 C. 等腰直角三角形 D. 等腰或直角三角形
8.在中,厘米,厘米,若利用正弦定理解有两解,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.对于任意的平面向量,,,下列说法错误的是( )
A. 若且,则
B.
C. 若,且,则
D.
10.已知,,下列命题正确的是( )
A.
B.
C. 若,则,至少有个为
D. 若,是两个虚数,,,则,为共轭复数
11.已知的内角,,所对的边分别为,,,则下列命题正确的是( )
A. 若,则一定为等腰三角形
B. 若,则
C. 若::::,则的最大内角为
D. 若为锐角三角形,则
三、填空题:本题共3小题,每小题5分,共15分。
12.若在中,,,,则 ______.
13.的最大值为______.
14.已知复数在复平面内对应的点为,且满足,为原点,,求的取值范围______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
求值:
;
;
.
16.本小题分
如图,在平面四边形中,,,的面积为.
求的长;
若,,求的长.
17.本小题分
已知复数在复平面内对应的点在虚轴的正半轴上,复数.
求,的值;
求,的值.
18.本小题分
如图在中,,,设,.
用表示向量.
若,,,求.
若,,求.
19.本小题分
某公司欲生产一款迎春工艺品回馈消费者,工艺品的平面设计如图所示,该工艺品由直角和以为直径的半圆拼接而成,点为半圆上一点异于,,点在线段上,且满足已知,,设.
为了使工艺礼品达到最佳观赏效果,需满足,且达到最大当为何值时,工艺礼品达到最佳观赏效果?
为了工艺礼品达到最佳稳定性便于收藏,需满足,且达到最大当为何值时,工艺礼品达到最佳稳定性?并求此时的值.
答案和解析
1.【答案】
【解析】解:由题意,,解得.
故选:.
根据向量共线的坐标公式求解.
本题考查平面向量的应用,属于基础题.
2.【答案】
【解析】解:根据题意,复数是纯虚数,
则有且,则.
故选:.
根据题意,由纯虚数的定义可得关于的方程,解可得答案.
本题考查纯虚数的定义,注意复数的分类,属于基础题.
3.【答案】
【解析】解:因为,,
由正弦定理,可得,,
则.
故选:.
由已知利用正弦定理即可求解.
本题考查了正弦定理在解三角形中的应用,属于基础题.
4.【答案】
【解析】【分析】
此题考查了两角和与差的正切函数公式,以及根与系数的关系,属于基础题.
根据题意易得,,代入求解即可.
【解答】
解:,是方程的两个根,
,,
则.
故选:.
5.【答案】
【解析】解:因为与共线,不符合题意;
假设,则与共线,不符合题意;
,即与共线,不符合题意;
不存在实数,使得,即与不共线,符合题意.
故选:.
结合向量的共线定理及平面向量基本定理检验各选项即可判断.
本题主要考查了向量共线定理的应用,还考查了平面向量基本定理的应用,属于基础题.
6.【答案】
【解析】解:,,
,,
则在上的投影向量为:.
故选:.
根据已知条件,结合投影向量的公式,即可求解.
本题主要考查投影向量的公式,属于基础题.
7.【答案】
【解析】解:,
由余弦定理可得:,整理可得:,
,则的形状为等腰三角形.
故选:.
由余弦定理化简已知等式可求,即可得解三角形的形状.
本题主要考查了余弦定理在解三角形中的应用,熟练掌握余弦定理是解题的关键,属于基础题.
8.【答案】
【解析】解:如图,
,,则,
以为圆心,为半径画圆弧,要使有两个解,则圆弧和边应该有两个交点,
故CA且,即,
解得.
故选:.
以为圆心,为半径画圆弧,圆弧与边应该有两个交点,此时三角形有两解,数形结合即可求出的范围.
本题考查了数形结合的应用,属于基础题.
9.【答案】
【解析】解:且,当为零向量时,则与不一定共线,即A错误,
由向量乘法的分配律可得:,即B正确,
因为,则,又,则或,即C错误,
取为非零向量,且与垂直,与不垂直,则,,即D错误,
故选:.
平面向量共线的传递性可得A错误,由向量乘法的分配律可得B正确,由向量垂直的运算可得,D错误,得解.
本题考查了平面向量共线的传递性、向量乘法的分配律,向量垂直的运算,属基础题.
10.【答案】
【解析】解:当时,显然错误;
设,都是实数,
则,
所以,
,B正确;
若,则
故,至少有个为,C正确;
设,都是实数,则,
,
若,,则,
所以,,即,为共轭复数,D正确.
故选:.
由已知结合复数的四则运算及复数的基本概念检验各选项即可判断.
本题主要考查了复数的四则运算及复数的基本概念,属于中档题.
11.【答案】
【解析】解:对于,由和正弦定理得:,故A正确;
对于,由及余弦函数在单调递减,得,故B错误;
对于,由::::及大边对大角得,角最大,设,,,
则,,故C正确;
对于,由为锐角三角形得,,又正弦函数在单调递增,
,即,故D正确.
故选:.
根据三角形的基本性质及正、余弦定理,正余弦函数的单调性,逐项分析即可.
本题考查正、余弦定理,三角函数的性质和推理能力,属中档题.
12.【答案】
【解析】解:由余弦定理,得,
所以.
故答案为:.
根据题意,利用数量积的定义和余弦定理加以计算,可得的值.
本题主要考查余弦定理、平面向量的数量积的定义等知识,考查了计算能力,属于基础题.
13.【答案】
【解析】解:,
即函数的最大值为,当,即,时取等号.
故答案为:.
先结合二倍角公式进行化简,然后结合正弦函数的性质即可求解.
本题主要考查了正弦函数最值的求解,属于基础题.
14.【答案】
【解析】解:设,则,
设复平面内一点,
则有,
即点在以点为圆心,为半径的圆周上或圆内,
设直线与圆交于,两点,
则,,而,表示在上的投影,
由图可知,,,
则,,
又因为,,,
所以,
即,
所以的取值范围为
故答案为:
设,则,由复数的几何意义可知,点在以点为圆心,为半径的圆周上或圆内,再结合平面向量数量积的几何意义求解.
本题主要考查了复数的几何意义,考查了平面向量的数量积运算,属于中档题.
15.【答案】解:根据题意,;
;
【解析】由虚数单位的性质计算可得答案;
由复数的乘法公式计算可得答案;
由复数的除法公式计算可得答案.
本题考查复数的计算,注意复数的四则运算法则,属于基础题.
16.【答案】解:,,的面积为,
,
,
由余弦定理,得
,
;
由知中,,,
,,,
又,,
在中,由正弦定理,得,
即,.
【解析】根据,求出,再利用余弦定理得;
根据已知条件在中,求出,再利用正弦定理求出.
本题考查了正弦定理,余弦定理和面积公式的应用,熟练掌握正余弦定理和面积公式是解本题的关键,属基础题.
17.【答案】解:由在复平面内对应的点在虚轴的正半轴上,
可得,
又复数,
可得,
即,;
由可知,,
所以,
.
【解析】根据复数的几何意义及同角三角函数关系计算即可;
利用三角恒等变换计算即可.
本题主要考查了复数的几何意义,和差角公式,同角基本关系在三角化简求值中的应用,属于中档题.
18.【答案】解:由题意有:
;
;
由题意,,,,
则;
,由,,
可得,即,
解得,,
故.
【解析】由平面向量的线性运算即可求解;
由向量的模长公式代入数据求解;
由向量垂直的性质可得,,再根据夹角公式即可求得.
本题考查平面向量的线性运算及数量积运算,属中档题.
19.【答案】解:由题意可得,
因为,
在直角中,可得,,
在直角中,可得,,
可得
,
所以当,即时,的最大值为,
即时,工艺礼品达到最佳观赏效果;
在直角中,由,
因为,,,
可得,
因为,
所以在直角中,,
所以,,
所以
,
可得当时,工艺礼品达到最佳稳定性,此时取得最大值,且最大值为.
【解析】利用直角三角形的边角关系,求出的解析式,从而可得取得最大值时的值;
由等积法求出的值,再计算的最大值以及对应的值.
本题考查了解三角形以及三角函数的应用问题,也考查了运算求解能力,是中档题.
第1页,共1页
同课章节目录
