1.4.1 用空间向量研究直线、平面的位置关系 课时练习(含解析)
文档属性
| 名称 | 1.4.1 用空间向量研究直线、平面的位置关系 课时练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 239.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 00:00:00 | ||
图片预览



文档简介
1.4.1 用空间向量研究直线、平面的位置关系(2)
一、 单项选择题
1 (2023十堰联考)若直线l∥α,且直线l的一个方向向量为(2,m,1),平面α的一个法向量为(1,-1,2),则实数m的值为( )
A. 4 B. -6 C. -8 D. 8
2 (2023文山期中)已知直线l的方向向量为m,平面α的法向量为n,则“m·n=0”是“l∥α”的( )
A. 充要条件 B. 既不充分也不必要条件
C. 充分不必要条件 D. 必要不充分条件
3 (2024赤峰期末)已知平面α∥β,n=(-1,2,3)为平面α的法向量,则下列向量中是平面β的法向量的是( )
A. (1,-2,3) B. (3,-1,2)
C. (1,2,-3) D.
4 (2023高二课时练习)如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别为线段A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A. 相交 B. 平行
C. 垂直 D. MN在平面BB1C1C内
(第5题) (第6题)
5 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.若在线段AB上存在点D,使得AC1∥平面CDB1,则点D满足的条件为( )
A. AD=AB B. AD=AB
C. AD=AB D. AD=AB
6 (2023台州期中)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=4,E,F,G分别是棱C1D1,BC,CC1的中点,M是平面ABCD内一动点.若直线D1M与平面EFG平行,则·的最小值为( )
A. 2 B. 9 C. D.
二、 多项选择题
7 下列命题中,是真命题的有( )
A. 直线l的方向向量有无穷多个
B. 若两条直线平行,则它们的方向向量的方向相同或相反
C. 若向量a是直线l的一个方向向量,则向量ka也是直线l的一个方向向量
D. 两直线的方向向量平行,则两直线平行;两直线的方向向量垂直,则两直线垂直
8 已知空间中两条不同的直线l,m,两个不同的平面α,β,则下列说法中错误的是( )
A. 若直线l的一个方向向量为a=(1,-1,2),直线m的一个方向向量为 b=(2,-2,4),则l∥m
B. 若直线l的一个方向向量为a=(0,1,-1),平面α的一个法向量为n=(1,-1,-1),则l∥α
C. 若平面α,β的一个法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D. 若平面α经过三个点A(1,0,-1),B(0,-1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则 u+t=1
三、 填空题
9 (2024全国专题练习)已知平面α的一个法向量是(2,3,-1),平面β的一个法向量是(4,λ,-2).若α∥β,则实数λ的值是________.
10 (2023济宁期中)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=AA1=1,M,N分别是线段A1B1,AC1上的点,P是直线AC上的点,满足MN∥平面BB1C1C,MN⊥NP,且M,N不是三棱柱的顶点,则线段MP长的最小值为________.
11 (2023河南联考)在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,BC的中点,Q为直线B1C1上的点,且=λ.若BQ∥平面A1MN,则λ=________.
四、 解答题
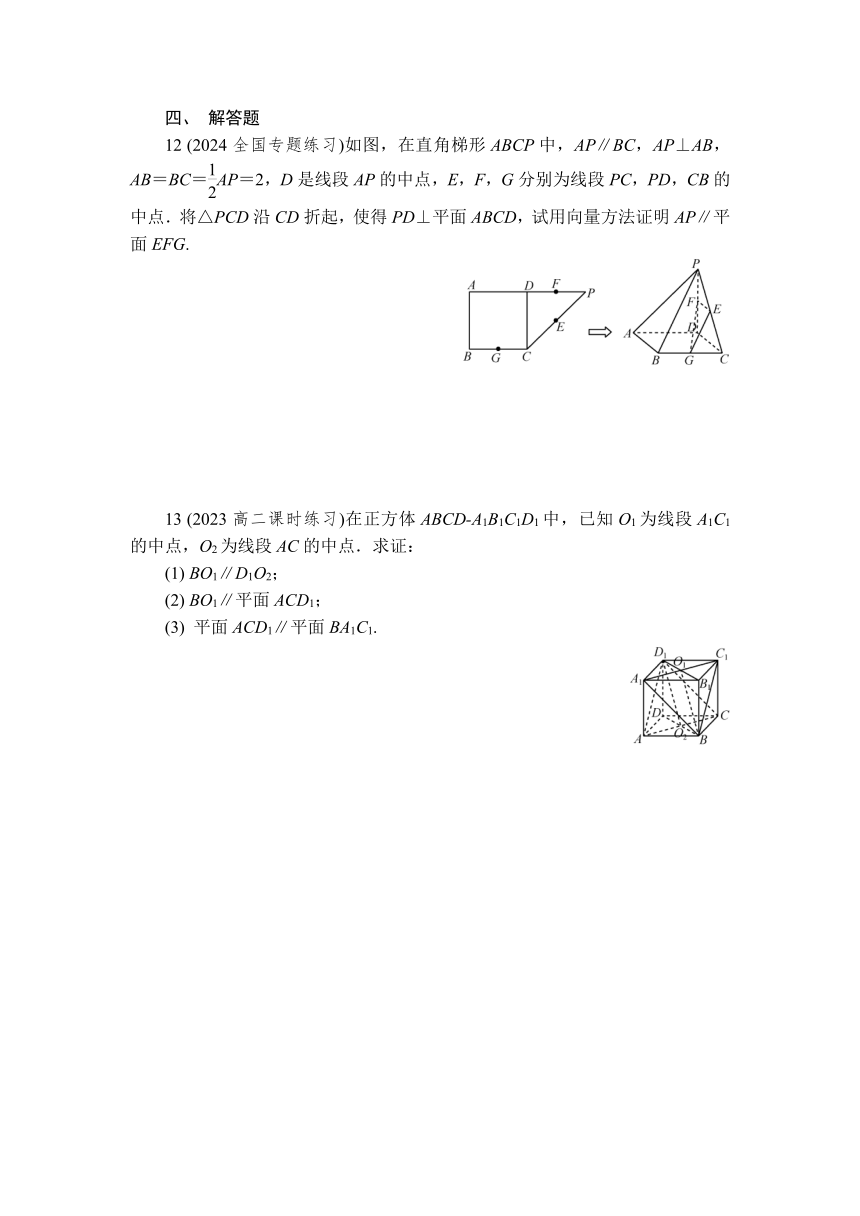
12 (2024全国专题练习)如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D是线段AP的中点,E,F,G分别为线段PC,PD,CB的中点.将△PCD沿CD折起,使得PD⊥平面ABCD,试用向量方法证明AP∥平面EFG.
13 (2023高二课时练习)在正方体ABCD-A1B1C1D1中,已知O1为线段A1C1的中点,O2为线段AC的中点.求证:
(1) BO1∥D1O2;
(2) BO1∥平面ACD1;
(3) 平面ACD1∥平面BA1C1.
【答案与解析】
1.4.1 用空间向量研究直线、平面的位置关系(2)
1. A 因为l∥α,直线l的一个方向向量为(2,m,1),平面α的一个法向量为(1,-1,2),所以(2,m,1)·(1,-1,2)=0,即2-m+2=0,解得m=4.
2. D 若m·n=0,则l∥α或l α,即充分性不成立.若l∥α,则m·n=0,即必要性成立.综上“m·n=0”是“l∥α”的必要不充分条件.
3. D 设平面β的法向量为m.因为α∥β,所以m∥n,即m=λn=(-λ,2λ,3λ).对于A,无解,故A错误;对于B,无解,故B错误;对于C,无解,故C错误;对于D, 解得λ=,故D正确.
4. B 以C1为坐标原点,C1B1,C1D1,C1C所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.因为A1M=AN=,所以M,N,则=.因为C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.因为·=-×0+0×a+×0=0,所以⊥.又MN 平面BB1C1C,所以MN与平面BB1C1C的位置关系是平行.
5. B 因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,所以AC⊥BC,则在直三棱柱ABCA1B1C1中,AC,BC,CC1两两垂直,以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则C(0,0,0),A(3,0,0),B(0,4,0),B1(0,4,4),C1(0,0,4),=(0,4,4).设点D(x,y,0)(0≤x≤3,0≤y≤4),则=(x,y,0),设平面CDB1的法向量为m=(a,b,c),则即令b=-x,则m=(y,-x,x).若AC1∥平面CDB1,则·m=0,易得=(-3,0,4),所以-3y+4x=0①.由点D 在线段AB上,得=,即4x+3y=12②,由①②可得x=,y=2,即D为线段AB的中点,故 AD=AB.
6. C 建立如图所示的空间直角坐标系,则E(2,3,3),F,G,D1(0,3,3),B1(4,0,3),M(x,y,0),所以=,=,=(x,y-3,-3).设平面EFG的法向量为n=(a,b,c),则即令b=1,则a=-,c=-1,即n=.因为直线D1M与平面EFG平行,所以·n=0,即-x+y-3+3=0,即y=x.因为=(4-x,-y,3),=(-x,3-y,3),所以·=(4-x)·(-x)+(-y)·(3-y)+9=x2-4x+y2-3y+9=x2-4x+-+9=x2-x+9=(x-2)2+.因为x∈(0,4),所以当x=2时,·取得最小值.
7. AB 对于A,B,由直线的方向向量的定义易知A,B正确;对于C,当k=0时,结论不成立,故C错误;对于D,两直线的方向向量平行,则两直线平行或重合,故D错误.故选AB.
8. BCD 对于A,b=2a,则a∥b,所以l∥m,故A正确;对于B,a·n=0×1+1×(-1)+(-1)×(-1)=0,则a⊥n,所以l∥α或l α,故B错误;对于C,若n1=λn2(λ≠0),则(0,1,3)=λ(1,0,2),得此方程组无解,所以α∥β不成立,故C错误;对于D,=(-1,-1,1),=(-1,3,0).因为n=(1,u,t)是平面α的法向量,所以解得u=,t=,所以u+t=,故D错误.故选BCD.
9. 6 因为α∥β,所以==,解得λ=6.
10. 由题意,得AB,AC,AA1两两互相垂直,则以A为坐标原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则B(2,0,0),C(0,1,0),B1(2,0,1),C1(0,1,1).设M(m,0,1),N(0,n,n),P(0,t,0),其中011. 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系.设AB=2,则A1(2,0,2),M(0,1,2),N(1,2,0),B(2,2,0),B1(2,2,2),C1(0,2,2),所以=(-2,1,0),=(-1,2,-2),=(-2,0,0).由=λ,得Q(2-2λ,2,2),则=(-2λ,0,2).由题意知,向量,,共面,故 t,s∈R,使得=t+s,即解得则λ=.
12. 由题意可知底面ABCD为正方形.
因为PD⊥平面ABCD,DA 平面ABCD,DC 平面ABCD,
所以DA,DC,DP两两垂直,
故以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,则P(0,0,2),C(0,2,0),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0),
所以=(-2,0,2),=(0,-1,0),=(1,1,-1).
设平面EFG的法向量为n=(x,y,z),
则
取x=1,可得n=(1,0,1).
因为n·=-2+0+2=0,AP 平面EFG,
所以AP∥平面EFG.
13. (1) 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.
设正方体的棱长为1,则B(1,1,0),O1,D1(0,0,1),O2,
所以=,=,
所以=-,
所以∥,即BO1∥D1O2.
(2) 设平面ACD1的法向量为n=(x,y,z).
因为A(1,0,0),C(0,1,0),D1=(0,0,1),
所以=(-1,1,0),=(-1,0,1).
由得即
令x=1,则y=1,z=1,所以n=(1,1,1).
又=,
所以n·=-×1+×1+1×1=0,
所以n⊥.
又BO1 平面ACD1,所以BO1∥平面ACD1.
(3) 方法一:因为A1(1,0,1),C1(0,1,1),
所以=(-1,1,0).
又=(-1,1,0),
所以=,所以AC∥A1C1.
因为AC 平面ACD1,A1C1 平面ACD1,
所以A1C1∥平面ACD1.
又由(2)知BO1∥平面ACD1,且A1C1∩BO1=O1,
A1C1 平面BA1C1,BO1 平面BA1C1,
所以平面ACD1∥平面BA1C1.
方法二:设平面BA1C1的法向量为u=(x1,y1,z1),
则即即
令x1=1,得y1=1,z1=1,所以u=(1,1,1).
由(2)知平面ACD1的一个法向量为n=(1,1,1),
所以n=u,所以n∥u,
则平面ACD1∥平面BA1C1.
一、 单项选择题
1 (2023十堰联考)若直线l∥α,且直线l的一个方向向量为(2,m,1),平面α的一个法向量为(1,-1,2),则实数m的值为( )
A. 4 B. -6 C. -8 D. 8
2 (2023文山期中)已知直线l的方向向量为m,平面α的法向量为n,则“m·n=0”是“l∥α”的( )
A. 充要条件 B. 既不充分也不必要条件
C. 充分不必要条件 D. 必要不充分条件
3 (2024赤峰期末)已知平面α∥β,n=(-1,2,3)为平面α的法向量,则下列向量中是平面β的法向量的是( )
A. (1,-2,3) B. (3,-1,2)
C. (1,2,-3) D.
4 (2023高二课时练习)如图,在棱长为a的正方体ABCD-A1B1C1D1中,M,N分别为线段A1B和AC上的点,A1M=AN=,则MN与平面BB1C1C的位置关系是( )
A. 相交 B. 平行
C. 垂直 D. MN在平面BB1C1C内
(第5题) (第6题)
5 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4.若在线段AB上存在点D,使得AC1∥平面CDB1,则点D满足的条件为( )
A. AD=AB B. AD=AB
C. AD=AB D. AD=AB
6 (2023台州期中)如图,在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=4,E,F,G分别是棱C1D1,BC,CC1的中点,M是平面ABCD内一动点.若直线D1M与平面EFG平行,则·的最小值为( )
A. 2 B. 9 C. D.
二、 多项选择题
7 下列命题中,是真命题的有( )
A. 直线l的方向向量有无穷多个
B. 若两条直线平行,则它们的方向向量的方向相同或相反
C. 若向量a是直线l的一个方向向量,则向量ka也是直线l的一个方向向量
D. 两直线的方向向量平行,则两直线平行;两直线的方向向量垂直,则两直线垂直
8 已知空间中两条不同的直线l,m,两个不同的平面α,β,则下列说法中错误的是( )
A. 若直线l的一个方向向量为a=(1,-1,2),直线m的一个方向向量为 b=(2,-2,4),则l∥m
B. 若直线l的一个方向向量为a=(0,1,-1),平面α的一个法向量为n=(1,-1,-1),则l∥α
C. 若平面α,β的一个法向量分别为n1=(0,1,3),n2=(1,0,2),则α∥β
D. 若平面α经过三个点A(1,0,-1),B(0,-1,0),C(-1,2,0),向量n=(1,u,t)是平面α的法向量,则 u+t=1
三、 填空题
9 (2024全国专题练习)已知平面α的一个法向量是(2,3,-1),平面β的一个法向量是(4,λ,-2).若α∥β,则实数λ的值是________.
10 (2023济宁期中)如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=2,AC=AA1=1,M,N分别是线段A1B1,AC1上的点,P是直线AC上的点,满足MN∥平面BB1C1C,MN⊥NP,且M,N不是三棱柱的顶点,则线段MP长的最小值为________.
11 (2023河南联考)在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,BC的中点,Q为直线B1C1上的点,且=λ.若BQ∥平面A1MN,则λ=________.
四、 解答题
12 (2024全国专题练习)如图,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=AP=2,D是线段AP的中点,E,F,G分别为线段PC,PD,CB的中点.将△PCD沿CD折起,使得PD⊥平面ABCD,试用向量方法证明AP∥平面EFG.
13 (2023高二课时练习)在正方体ABCD-A1B1C1D1中,已知O1为线段A1C1的中点,O2为线段AC的中点.求证:
(1) BO1∥D1O2;
(2) BO1∥平面ACD1;
(3) 平面ACD1∥平面BA1C1.
【答案与解析】
1.4.1 用空间向量研究直线、平面的位置关系(2)
1. A 因为l∥α,直线l的一个方向向量为(2,m,1),平面α的一个法向量为(1,-1,2),所以(2,m,1)·(1,-1,2)=0,即2-m+2=0,解得m=4.
2. D 若m·n=0,则l∥α或l α,即充分性不成立.若l∥α,则m·n=0,即必要性成立.综上“m·n=0”是“l∥α”的必要不充分条件.
3. D 设平面β的法向量为m.因为α∥β,所以m∥n,即m=λn=(-λ,2λ,3λ).对于A,无解,故A错误;对于B,无解,故B错误;对于C,无解,故C错误;对于D, 解得λ=,故D正确.
4. B 以C1为坐标原点,C1B1,C1D1,C1C所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系.因为A1M=AN=,所以M,N,则=.因为C1D1⊥平面BB1C1C,所以=(0,a,0)为平面BB1C1C的一个法向量.因为·=-×0+0×a+×0=0,所以⊥.又MN 平面BB1C1C,所以MN与平面BB1C1C的位置关系是平行.
5. B 因为AC=3,BC=4,AB=5,所以AC2+BC2=AB2,所以AC⊥BC,则在直三棱柱ABCA1B1C1中,AC,BC,CC1两两垂直,以C为坐标原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,则C(0,0,0),A(3,0,0),B(0,4,0),B1(0,4,4),C1(0,0,4),=(0,4,4).设点D(x,y,0)(0≤x≤3,0≤y≤4),则=(x,y,0),设平面CDB1的法向量为m=(a,b,c),则即令b=-x,则m=(y,-x,x).若AC1∥平面CDB1,则·m=0,易得=(-3,0,4),所以-3y+4x=0①.由点D 在线段AB上,得=,即4x+3y=12②,由①②可得x=,y=2,即D为线段AB的中点,故 AD=AB.
6. C 建立如图所示的空间直角坐标系,则E(2,3,3),F,G,D1(0,3,3),B1(4,0,3),M(x,y,0),所以=,=,=(x,y-3,-3).设平面EFG的法向量为n=(a,b,c),则即令b=1,则a=-,c=-1,即n=.因为直线D1M与平面EFG平行,所以·n=0,即-x+y-3+3=0,即y=x.因为=(4-x,-y,3),=(-x,3-y,3),所以·=(4-x)·(-x)+(-y)·(3-y)+9=x2-4x+y2-3y+9=x2-4x+-+9=x2-x+9=(x-2)2+.因为x∈(0,4),所以当x=2时,·取得最小值.
7. AB 对于A,B,由直线的方向向量的定义易知A,B正确;对于C,当k=0时,结论不成立,故C错误;对于D,两直线的方向向量平行,则两直线平行或重合,故D错误.故选AB.
8. BCD 对于A,b=2a,则a∥b,所以l∥m,故A正确;对于B,a·n=0×1+1×(-1)+(-1)×(-1)=0,则a⊥n,所以l∥α或l α,故B错误;对于C,若n1=λn2(λ≠0),则(0,1,3)=λ(1,0,2),得此方程组无解,所以α∥β不成立,故C错误;对于D,=(-1,-1,1),=(-1,3,0).因为n=(1,u,t)是平面α的法向量,所以解得u=,t=,所以u+t=,故D错误.故选BCD.
9. 6 因为α∥β,所以==,解得λ=6.
10. 由题意,得AB,AC,AA1两两互相垂直,则以A为坐标原点,AB,AC,AA1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则B(2,0,0),C(0,1,0),B1(2,0,1),C1(0,1,1).设M(m,0,1),N(0,n,n),P(0,t,0),其中0
12. 由题意可知底面ABCD为正方形.
因为PD⊥平面ABCD,DA 平面ABCD,DC 平面ABCD,
所以DA,DC,DP两两垂直,
故以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向,建立如图所示的空间直角坐标系,则P(0,0,2),C(0,2,0),G(1,2,0),E(0,1,1),F(0,0,1),A(2,0,0),
所以=(-2,0,2),=(0,-1,0),=(1,1,-1).
设平面EFG的法向量为n=(x,y,z),
则
取x=1,可得n=(1,0,1).
因为n·=-2+0+2=0,AP 平面EFG,
所以AP∥平面EFG.
13. (1) 以D为坐标原点,,,的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系.
设正方体的棱长为1,则B(1,1,0),O1,D1(0,0,1),O2,
所以=,=,
所以=-,
所以∥,即BO1∥D1O2.
(2) 设平面ACD1的法向量为n=(x,y,z).
因为A(1,0,0),C(0,1,0),D1=(0,0,1),
所以=(-1,1,0),=(-1,0,1).
由得即
令x=1,则y=1,z=1,所以n=(1,1,1).
又=,
所以n·=-×1+×1+1×1=0,
所以n⊥.
又BO1 平面ACD1,所以BO1∥平面ACD1.
(3) 方法一:因为A1(1,0,1),C1(0,1,1),
所以=(-1,1,0).
又=(-1,1,0),
所以=,所以AC∥A1C1.
因为AC 平面ACD1,A1C1 平面ACD1,
所以A1C1∥平面ACD1.
又由(2)知BO1∥平面ACD1,且A1C1∩BO1=O1,
A1C1 平面BA1C1,BO1 平面BA1C1,
所以平面ACD1∥平面BA1C1.
方法二:设平面BA1C1的法向量为u=(x1,y1,z1),
则即即
令x1=1,得y1=1,z1=1,所以u=(1,1,1).
由(2)知平面ACD1的一个法向量为n=(1,1,1),
所以n=u,所以n∥u,
则平面ACD1∥平面BA1C1.
