12.1 杠杆 课件(共49张PPT) 023~2024学年人教版物理八年级下册
文档属性
| 名称 | 12.1 杠杆 课件(共49张PPT) 023~2024学年人教版物理八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-01 00:00:00 | ||
图片预览








文档简介
(共49张PPT)
杠杆
12.1 杠杆
探究新知
它们工作时有什么共同特征?
当你使用这些工具时,你就在使用杠杆了。
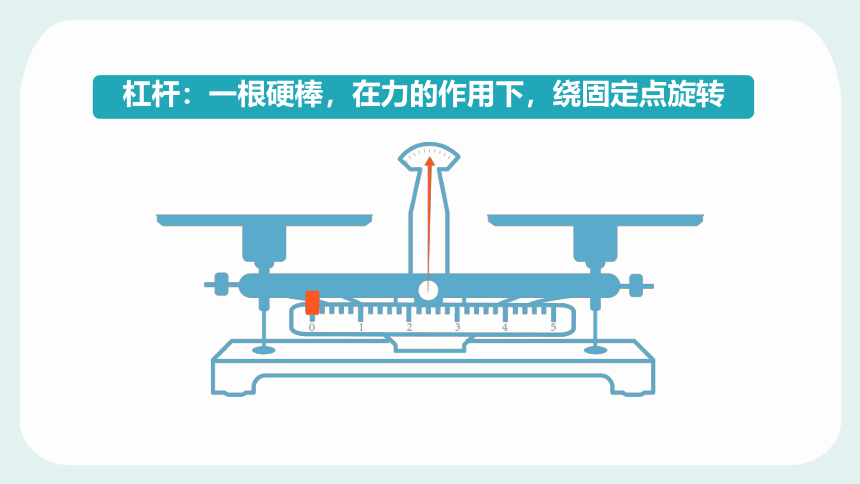
杠杆:一根硬棒,在力的作用下,绕固定点旋转
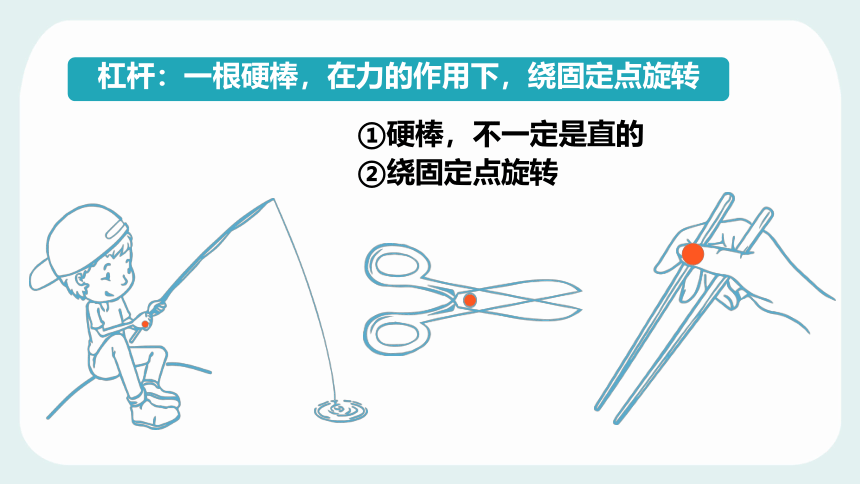
杠杆:一根硬棒,在力的作用下,绕固定点旋转
杠杆:一根硬棒,在力的作用下,绕固定点旋转
①硬棒,不一定是直的
杠杆:一根硬棒,在力的作用下,绕固定点旋转
①硬棒,不一定是直的
②绕固定点旋转
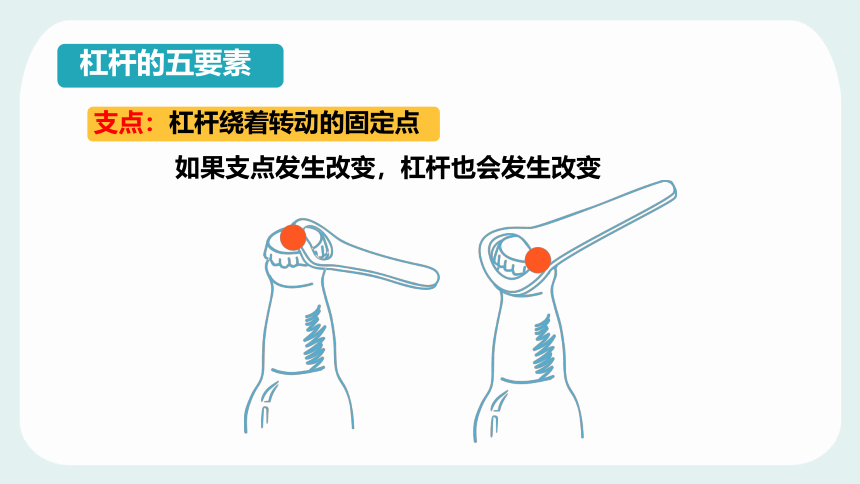
如果支点发生改变,杠杆也会发生改变
杠杆的五要素
支点:杠杆绕着转动的固定点
A为支点
杠杆的五要素
判断支点:使杠杆旋转,绕着某一点旋转
支点
B为向上旋转时的支点
杠杆的五要素
判断支点:使杠杆旋转,绕着某一点旋转
支点
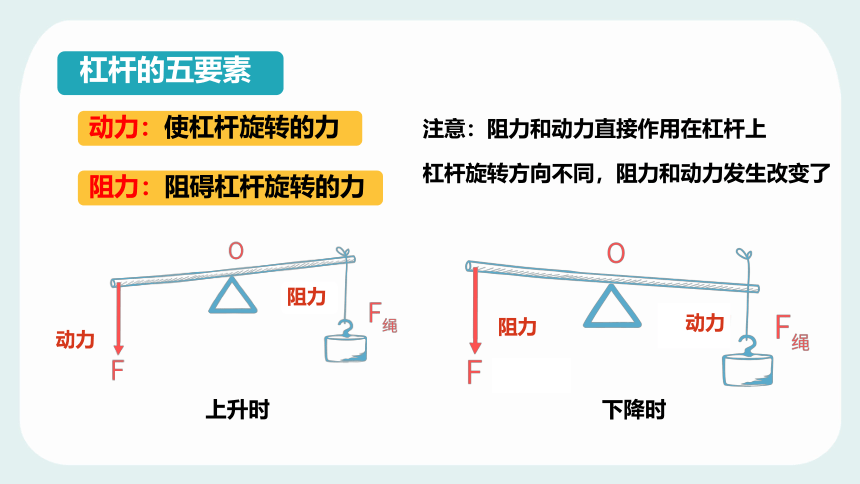
杠杆的五要素
动力:使杠杆旋转的力
注意:阻力和动力直接作用在杠杆上
阻力:阻碍杠杆旋转的力
杠杆旋转方向不同,阻力和动力发生改变了
上升时
下降时
动力
阻力
动力
阻力
杠杆的五要素
动力臂:
阻力臂:
大小就是支点到力作用线垂线段的长度
在几何上,力臂和力的作用线是相互垂直的
l1是F1的力臂
l2是F2的力臂
在描述力臂时,一定指出是哪个力的力臂
支点到动力作用线的距离
支点到阻力作用线的距离
l1
l2
杠杆画图
如图,渔民用杠杆和滑轮的组合机械起吊渔网,请画出杠杆OBA所受
动力的力臂l1和阻力F2的示意图。
例题
动力和阻力是直接作用在杠杆上
绕O点旋转
F2
F 阻碍旋转
F2 = G
F1
F 使杠杆旋转
(动力)
支点
l1
例题
l1
如图,渔民用杠杆和滑轮的组合机械起吊渔网,请画出杠杆OBA所受
动力的力臂l1和阻力F2的示意图。
力臂:是从支点出发,画出力的作用线的垂线段
在几何关系上,力和力臂是相互垂直的
轻质杠杆(不考虑重力)
已知力,画力臂
l1
l2
已知力臂画力
力和力臂是相互垂直的
力的方向
在支点同侧时
相反侧
F1
F
在支点异侧时
同一侧
F1
F
杠杆平衡
杠杆平衡状态:杠杆静止或匀速转动
实验探究
实验器材:杠杆(含支架)、钩码、细绳
实验步骤:
①使支架在杠杆中心:目的是避免杠杆自身重力对实验的影响
②调节平衡螺母,使杠杆处于水平状态,目的是可以方便读取力臂
③在杠杆一侧挂上适量钩码,在另一侧的某一位置也挂上适量钩码,
使杠杆依旧保持在水平状态
④改变钩码数量和钩码位置,多次实验
⑤设计表格,记录数据
F1l1 = F2l2
动力×动力臂=阻力×阻力臂
F1
l1
F2
l2
平衡螺母
F1l1 = F2l2
受力分析:
F1 = G = 30N
F2 = mg
∴ m = 5kg
F1l1 = F2l2
→
F2 =
O
5cm
3cm
3kg
m= kg
F1
F2
例1.如图所示一块均匀的厚木板长15m,重400N,对称地搁在相距8m的A、B两个支架上,一个体重为500N的人,从A点出发向左走到离A点 m处时,木板开始翘动。
3.2
杠杆平衡条件:
①受力分析
②代入F1l1 = F2l2
支点为A
FX = G×4m
=
X =
= 3.2m
G
4m
X
F
杠杆平衡判断
杠杆平衡的判断:
力×力臂-力×力臂
若F1l1 - F2l2>0 向 F1 偏转
若F1l1 - F2l2 = 0 平衡
若F1l1 - F2l2<0 向 F2 偏转
OA<OB,杠杆平衡
①若将G1G2同时向支点O移动相同距离
<0
∴右端下沉
移动前:G1×OA = G2×OB
移动后:
= G1OA - G2OB + G2l - G1l
= 0 + G2l - G1l
→G1>G2
O
A
B
G1
G2
F1=G1
F2=G2
G1
F1=G1
G2
F2=G2
G1×(OA - l)-G2×(OB - l)
l
l
<0
<0
②V1=V2
浸入前:
G1OA = G2OB
(G1-F浮)× OA -(G2 - F浮)× OB
浸入后:
= G1OA - G2OB + F浮OB - F浮OA
∴A端下沉
O
A
B
G1
G2
浸入水中
(OA<OB)
F1=G1 - F浮
F2=G2 - F浮
F浮 = ρ水gV排
>0
>0
= 0
③V1 = V2 切去相同体积V
切去前:G1OA = G2OB
→ ρ1V1gOA = ρ2V2gOB
→ ρ1OA = ρ2OB
切去后:(G1- G)× OA -(G2-G')× OB
=G1OA - G2OB + G'OB - GOA
= G’OB - GOA
=ρ2VgOB - ρ1VgOA
=Vg(ρ2OB - ρ1OA)
∴依旧平衡
O
A
B
G1
G2
= 0
= 0
杠杆分类
动力 ×动力臂=阻力×阻力臂
动力<阻力
①动力臂>阻力臂
省力杠杆(铡刀、开瓶器)
动力 ×动力臂=阻力×阻力臂
动力=阻力
②动力臂=阻力臂
等臂杠杆(托盘天平)
动力 ×动力臂=阻力×阻力臂
动力>阻力
③动力臂<阻力臂
费力杠杆(坩埚钳、理发用剪刀)
如图是指甲刀的架构图,关于指甲刀下面说法正确的是( )
A、指甲刀可以看成是一个省力杠杆和一个费力杠杆组成
B、指甲刀可以看成是一个省力杠杆和两个费力杠杆组成
C、指甲刀使用的越久,用它剪指甲就越省力
D、用指甲刀剪指甲时,大段地往下剪比小段地往下剪省力
B
阻力臂<动力臂
阻力臂>动力臂
阻力臂 = 动力臂
是省力杠杆
是等臂杠杆
是省力杠杆
A
D
C
B
F
E
O
三个杠杆:
ABC
DBO
EFO
支点为B
动力臂>阻力臂
省力杠杆
支点为O
动力臂 < 阻力臂
费力杠杆
支点为O
动力臂 < 阻力臂
费力杠杆
杠杆最小力问题
画最大力臂
求最小力 F1l1 = F2l2
定值
最小
最大
求最小力实际上是确定最大力臂
非轻质杠杆
方向相同
力的方向相同时,支点越远的力的作用点
施力的力越小
G·LG = Fl
lb>la
O
G
a
b
Fa
Fb
Fb<Fa
la
lb
画最大力臂
求最小力 F1l1 = F2l2
定值
最小
最大
求最小力实际上是确定最大力臂
la < lb
GlG = FlF
lb最大,Fb最小
支点到离支点最远的力的作用点的连线
最小的力:垂直于最大的力臂
定值
O
G
lG
Fa
Fb
Fc
la
lb
lG
lc<lb
AO = 2OB
最小的力
从支点到离支点最远的力的连线
F × OA = F1 × OB
F =
例题
= 20N
G=40N
最大的力臂
F
F1=G=40N
例题
最小的力
GlG = FlF
LG =
LF = 2R
∴
最大的力臂
从支点与离支点最远的
力的作用点的连线
F
G
lG
lF
F =
=
G
杠杆无浮力计算
①找支点
②受力分析(力一定直接作用在杠杆上)
③画力臂
④代入 F1l1 = F2l2
OA:OB=1:3,求此时物体对地面的压力
F1 + FN = G
FN = 30N
∴F压 =
F1×OA = F×OB
F1 = 30N
F1
G=60N
F1=30N
FN
FN = 30N
①找支点、O
②受力分析
③画力臂
④代入计算
l = 1m,力作用在杠杆上,力的作用点离 O 点距离和 F 大小的关系如图所示,
求杆的重力。
GlG = FlF
G × 0.5m =
G = 20N
非轻质杠杆
G
lF
lG
10N·m
以 为半径,切去一个内切球,问剩余部分的重心位置离球心的距离
先补起来,整球放在桌面上是平衡的
杠杆平衡,支点为O点向桌面的投影
设切去后质量为M,切去质量为m
M = ρV1
A
O
B
G1
G2
AO
m = ρV2
MgAO = mg R
=
∴
AO = R
即重心离球心的距离为 R
杠杆有浮力计算
当物体在空气中时,F = F1
当物体浸没在水中,F = F2,求物体密度
浸入前:
GOA= F1OB ①
OA:OB = 1:3 ②
浸入后:
(G-F浮)OA = F2 OB ③
V排 = V物 ④
:
F浮 = ρ液gV排 G = ρ物V物g
轻质杠杆
O
OA = AB = 1:2
A
B
G
F
FA=G
F1
FA=G-F浮
F2
GB·OC = GA·OE ①
①测金属密度:
将物体完全浸入水中,调整物体A至D点,平衡
(GB-F浮)· OC = GA·OD ②
∴ ρB =
:
物体B挂在C端,物体A挂在E端,平衡
F1 = GB
F2 = GA
F2 = GA
D
F1 = GB
F2 = GA
F2 = GA
②测液体密度:
GB·OC = GA·OE ①
物体放入液体中,物体A调整至D点,平衡
(GB-F浮)·OC = GA·OD ②
:
已知 ρB 物体B挂在c端,物体A挂在E端,平衡
F1 = GB -F浮
D
杠杆动态分析
杠杆动态分析:
①在初始状态对杠杆进行分析,得到杠杆平衡关系等式
②按题意找到杠杆另一状态并对其进行分析,与①情况下的有关量进行比较,
得到所求结果
竖直向上,方向不变
初始状态:
∴F = F'
拉动过程中:
GlG' = F'lF'
GlG = FlF
G
lG
lF
F'
G
lG'
O
lF'
F垂直于杆,将杆拉到水平位置
∴F = 0
lG = 0
初始状态:
F'lF' = GlG'
∴拉力F 变大
F
F lF = G lG
G
lF
F'
G
lG'
lF'
lG'
F'
G
lF'
杆 秤
不挂物体时:
OA
挂上质量为m物体:
G砣(OA+OB)
mg·OD = G砣·AB
∴杆秤刻度是均匀的
铁钩
0刻度线
秤砣
G杆
G杆·
OC =
G砣·
G砣
B
mg
G杆·OC +
mg·OD
= G砣·OB =
m =
买东西时,商贩将秤砣质量减小
卖东西时,商贩将秤砣质量变大
杆秤 秤砣质量变小,读数大于实际,偏大
秤砣质量增大,读数小于实际,偏小
买到的实际质量<读数
m =
读数
减小
实际
卖出去实际质量>读数
m =
读数
增大
实际
(一定)
(变大)
(减小)
杠杆
12.1 杠杆
探究新知
它们工作时有什么共同特征?
当你使用这些工具时,你就在使用杠杆了。
杠杆:一根硬棒,在力的作用下,绕固定点旋转
杠杆:一根硬棒,在力的作用下,绕固定点旋转
杠杆:一根硬棒,在力的作用下,绕固定点旋转
①硬棒,不一定是直的
杠杆:一根硬棒,在力的作用下,绕固定点旋转
①硬棒,不一定是直的
②绕固定点旋转
如果支点发生改变,杠杆也会发生改变
杠杆的五要素
支点:杠杆绕着转动的固定点
A为支点
杠杆的五要素
判断支点:使杠杆旋转,绕着某一点旋转
支点
B为向上旋转时的支点
杠杆的五要素
判断支点:使杠杆旋转,绕着某一点旋转
支点
杠杆的五要素
动力:使杠杆旋转的力
注意:阻力和动力直接作用在杠杆上
阻力:阻碍杠杆旋转的力
杠杆旋转方向不同,阻力和动力发生改变了
上升时
下降时
动力
阻力
动力
阻力
杠杆的五要素
动力臂:
阻力臂:
大小就是支点到力作用线垂线段的长度
在几何上,力臂和力的作用线是相互垂直的
l1是F1的力臂
l2是F2的力臂
在描述力臂时,一定指出是哪个力的力臂
支点到动力作用线的距离
支点到阻力作用线的距离
l1
l2
杠杆画图
如图,渔民用杠杆和滑轮的组合机械起吊渔网,请画出杠杆OBA所受
动力的力臂l1和阻力F2的示意图。
例题
动力和阻力是直接作用在杠杆上
绕O点旋转
F2
F 阻碍旋转
F2 = G
F1
F 使杠杆旋转
(动力)
支点
l1
例题
l1
如图,渔民用杠杆和滑轮的组合机械起吊渔网,请画出杠杆OBA所受
动力的力臂l1和阻力F2的示意图。
力臂:是从支点出发,画出力的作用线的垂线段
在几何关系上,力和力臂是相互垂直的
轻质杠杆(不考虑重力)
已知力,画力臂
l1
l2
已知力臂画力
力和力臂是相互垂直的
力的方向
在支点同侧时
相反侧
F1
F
在支点异侧时
同一侧
F1
F
杠杆平衡
杠杆平衡状态:杠杆静止或匀速转动
实验探究
实验器材:杠杆(含支架)、钩码、细绳
实验步骤:
①使支架在杠杆中心:目的是避免杠杆自身重力对实验的影响
②调节平衡螺母,使杠杆处于水平状态,目的是可以方便读取力臂
③在杠杆一侧挂上适量钩码,在另一侧的某一位置也挂上适量钩码,
使杠杆依旧保持在水平状态
④改变钩码数量和钩码位置,多次实验
⑤设计表格,记录数据
F1l1 = F2l2
动力×动力臂=阻力×阻力臂
F1
l1
F2
l2
平衡螺母
F1l1 = F2l2
受力分析:
F1 = G = 30N
F2 = mg
∴ m = 5kg
F1l1 = F2l2
→
F2 =
O
5cm
3cm
3kg
m= kg
F1
F2
例1.如图所示一块均匀的厚木板长15m,重400N,对称地搁在相距8m的A、B两个支架上,一个体重为500N的人,从A点出发向左走到离A点 m处时,木板开始翘动。
3.2
杠杆平衡条件:
①受力分析
②代入F1l1 = F2l2
支点为A
FX = G×4m
=
X =
= 3.2m
G
4m
X
F
杠杆平衡判断
杠杆平衡的判断:
力×力臂-力×力臂
若F1l1 - F2l2>0 向 F1 偏转
若F1l1 - F2l2 = 0 平衡
若F1l1 - F2l2<0 向 F2 偏转
OA<OB,杠杆平衡
①若将G1G2同时向支点O移动相同距离
<0
∴右端下沉
移动前:G1×OA = G2×OB
移动后:
= G1OA - G2OB + G2l - G1l
= 0 + G2l - G1l
→G1>G2
O
A
B
G1
G2
F1=G1
F2=G2
G1
F1=G1
G2
F2=G2
G1×(OA - l)-G2×(OB - l)
l
l
<0
<0
②V1=V2
浸入前:
G1OA = G2OB
(G1-F浮)× OA -(G2 - F浮)× OB
浸入后:
= G1OA - G2OB + F浮OB - F浮OA
∴A端下沉
O
A
B
G1
G2
浸入水中
(OA<OB)
F1=G1 - F浮
F2=G2 - F浮
F浮 = ρ水gV排
>0
>0
= 0
③V1 = V2 切去相同体积V
切去前:G1OA = G2OB
→ ρ1V1gOA = ρ2V2gOB
→ ρ1OA = ρ2OB
切去后:(G1- G)× OA -(G2-G')× OB
=G1OA - G2OB + G'OB - GOA
= G’OB - GOA
=ρ2VgOB - ρ1VgOA
=Vg(ρ2OB - ρ1OA)
∴依旧平衡
O
A
B
G1
G2
= 0
= 0
杠杆分类
动力 ×动力臂=阻力×阻力臂
动力<阻力
①动力臂>阻力臂
省力杠杆(铡刀、开瓶器)
动力 ×动力臂=阻力×阻力臂
动力=阻力
②动力臂=阻力臂
等臂杠杆(托盘天平)
动力 ×动力臂=阻力×阻力臂
动力>阻力
③动力臂<阻力臂
费力杠杆(坩埚钳、理发用剪刀)
如图是指甲刀的架构图,关于指甲刀下面说法正确的是( )
A、指甲刀可以看成是一个省力杠杆和一个费力杠杆组成
B、指甲刀可以看成是一个省力杠杆和两个费力杠杆组成
C、指甲刀使用的越久,用它剪指甲就越省力
D、用指甲刀剪指甲时,大段地往下剪比小段地往下剪省力
B
阻力臂<动力臂
阻力臂>动力臂
阻力臂 = 动力臂
是省力杠杆
是等臂杠杆
是省力杠杆
A
D
C
B
F
E
O
三个杠杆:
ABC
DBO
EFO
支点为B
动力臂>阻力臂
省力杠杆
支点为O
动力臂 < 阻力臂
费力杠杆
支点为O
动力臂 < 阻力臂
费力杠杆
杠杆最小力问题
画最大力臂
求最小力 F1l1 = F2l2
定值
最小
最大
求最小力实际上是确定最大力臂
非轻质杠杆
方向相同
力的方向相同时,支点越远的力的作用点
施力的力越小
G·LG = Fl
lb>la
O
G
a
b
Fa
Fb
Fb<Fa
la
lb
画最大力臂
求最小力 F1l1 = F2l2
定值
最小
最大
求最小力实际上是确定最大力臂
la < lb
GlG = FlF
lb最大,Fb最小
支点到离支点最远的力的作用点的连线
最小的力:垂直于最大的力臂
定值
O
G
lG
Fa
Fb
Fc
la
lb
lG
lc<lb
AO = 2OB
最小的力
从支点到离支点最远的力的连线
F × OA = F1 × OB
F =
例题
= 20N
G=40N
最大的力臂
F
F1=G=40N
例题
最小的力
GlG = FlF
LG =
LF = 2R
∴
最大的力臂
从支点与离支点最远的
力的作用点的连线
F
G
lG
lF
F =
=
G
杠杆无浮力计算
①找支点
②受力分析(力一定直接作用在杠杆上)
③画力臂
④代入 F1l1 = F2l2
OA:OB=1:3,求此时物体对地面的压力
F1 + FN = G
FN = 30N
∴F压 =
F1×OA = F×OB
F1 = 30N
F1
G=60N
F1=30N
FN
FN = 30N
①找支点、O
②受力分析
③画力臂
④代入计算
l = 1m,力作用在杠杆上,力的作用点离 O 点距离和 F 大小的关系如图所示,
求杆的重力。
GlG = FlF
G × 0.5m =
G = 20N
非轻质杠杆
G
lF
lG
10N·m
以 为半径,切去一个内切球,问剩余部分的重心位置离球心的距离
先补起来,整球放在桌面上是平衡的
杠杆平衡,支点为O点向桌面的投影
设切去后质量为M,切去质量为m
M = ρV1
A
O
B
G1
G2
AO
m = ρV2
MgAO = mg R
=
∴
AO = R
即重心离球心的距离为 R
杠杆有浮力计算
当物体在空气中时,F = F1
当物体浸没在水中,F = F2,求物体密度
浸入前:
GOA= F1OB ①
OA:OB = 1:3 ②
浸入后:
(G-F浮)OA = F2 OB ③
V排 = V物 ④
:
F浮 = ρ液gV排 G = ρ物V物g
轻质杠杆
O
OA = AB = 1:2
A
B
G
F
FA=G
F1
FA=G-F浮
F2
GB·OC = GA·OE ①
①测金属密度:
将物体完全浸入水中,调整物体A至D点,平衡
(GB-F浮)· OC = GA·OD ②
∴ ρB =
:
物体B挂在C端,物体A挂在E端,平衡
F1 = GB
F2 = GA
F2 = GA
D
F1 = GB
F2 = GA
F2 = GA
②测液体密度:
GB·OC = GA·OE ①
物体放入液体中,物体A调整至D点,平衡
(GB-F浮)·OC = GA·OD ②
:
已知 ρB 物体B挂在c端,物体A挂在E端,平衡
F1 = GB -F浮
D
杠杆动态分析
杠杆动态分析:
①在初始状态对杠杆进行分析,得到杠杆平衡关系等式
②按题意找到杠杆另一状态并对其进行分析,与①情况下的有关量进行比较,
得到所求结果
竖直向上,方向不变
初始状态:
∴F = F'
拉动过程中:
GlG' = F'lF'
GlG = FlF
G
lG
lF
F'
G
lG'
O
lF'
F垂直于杆,将杆拉到水平位置
∴F = 0
lG = 0
初始状态:
F'lF' = GlG'
∴拉力F 变大
F
F lF = G lG
G
lF
F'
G
lG'
lF'
lG'
F'
G
lF'
杆 秤
不挂物体时:
OA
挂上质量为m物体:
G砣(OA+OB)
mg·OD = G砣·AB
∴杆秤刻度是均匀的
铁钩
0刻度线
秤砣
G杆
G杆·
OC =
G砣·
G砣
B
mg
G杆·OC +
mg·OD
= G砣·OB =
m =
买东西时,商贩将秤砣质量减小
卖东西时,商贩将秤砣质量变大
杆秤 秤砣质量变小,读数大于实际,偏大
秤砣质量增大,读数小于实际,偏小
买到的实际质量<读数
m =
读数
减小
实际
卖出去实际质量>读数
m =
读数
增大
实际
(一定)
(变大)
(减小)
