第十九章 一次函数单元同步检测试题(含答案)
文档属性
| 名称 | 第十九章 一次函数单元同步检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 16:06:46 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.一本笔记本5元,买本共付元,则5和分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
2.正比例函数的图象经过的象限是( )
A.第一、三象限 B.第二、四象限 C.第三、四象限 D.第一、二象限
3.已知正比例函数,若y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.如图,一次函数的图像经过A、B两点,则关于x的不等式的解集是( )
A. B. C. D.
7.已知一次函数和的图象都经过点,且与轴分别交于两点,那么的面积是( )
A.2 B.3 C.4 D.6
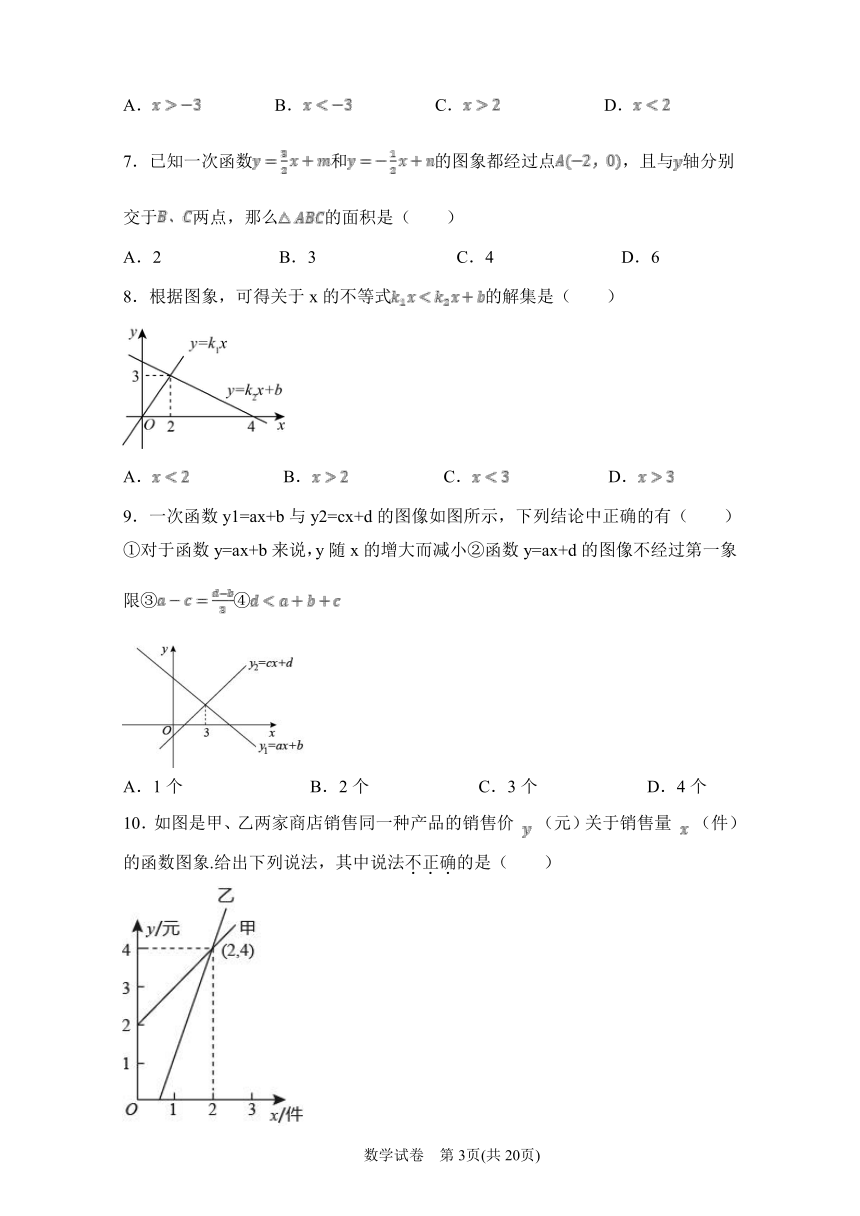
8.根据图象,可得关于x的不等式的解集是( )
A. B. C. D.
9.一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )
①对于函数y=ax+b来说,y随x的增大而减小②函数y=ax+d的图像不经过第一象限③④
A.1个 B.2个 C.3个 D.4个
10.如图是甲、乙两家商店销售同一种产品的销售价 (元)关于销售量 (件)的函数图象.给出下列说法,其中说法不正确的是( )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
二、填空题(每题3分,共30分)
11.点、是一次函数图象上的两个点,则 .
12.若一次函数的图像经过点,则不等式的解集为_________.
13.如果一次函数、为常数,的图像过点,且经过第一、二、三象限,那么当时,的取值范围是_________.
14.某一次函数的图象经过点(﹣1,2),且函数y的值随自变量x的增大而减小,请写出一个符合上述条件的函数关系式: .
15.若一次函数y=(1﹣2k)x+k的图象经过第一、二、三象限,则k的取值范围是 .
16.将函数y=2x的图象l1向上平移3个单位得到直线l2,则直线l2与坐标轴围成的三角形面积为 .
17.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,在第一象限内有一点,当时,m的值为_______.
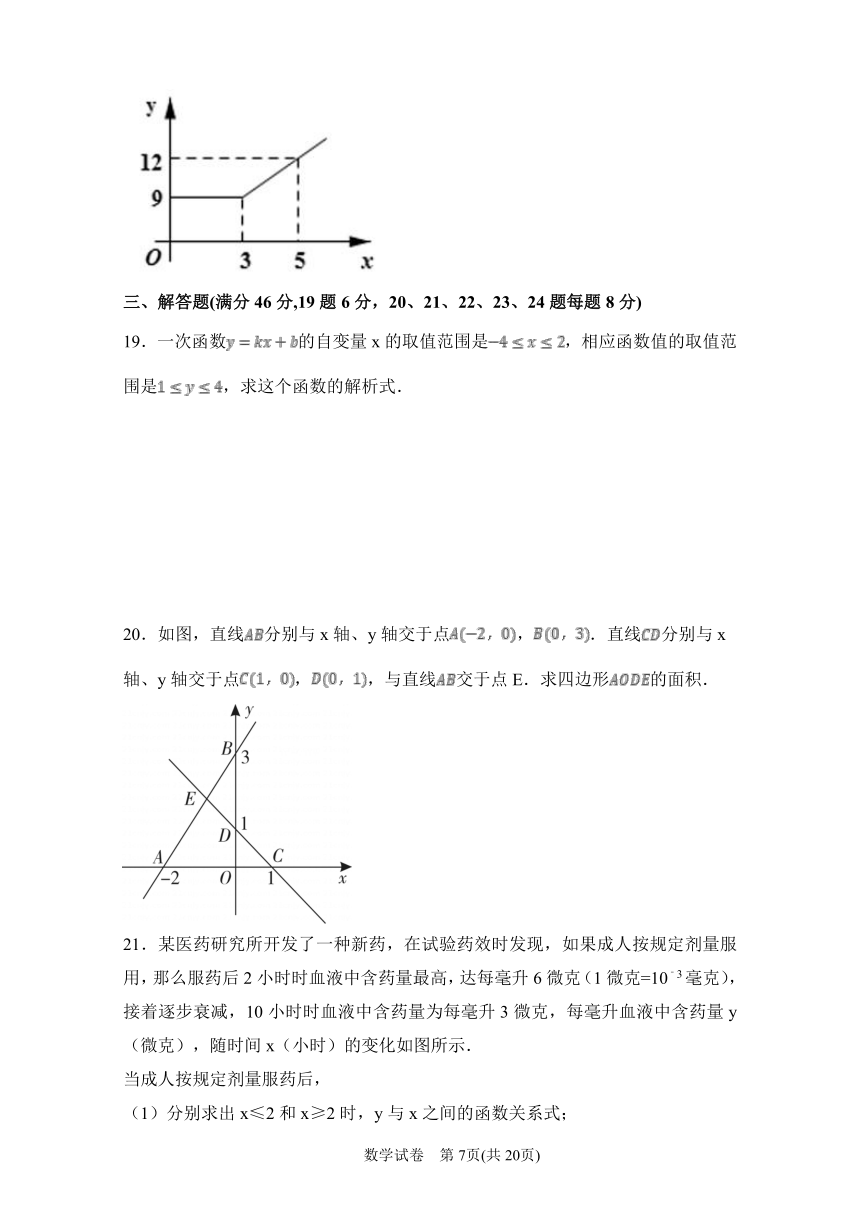
18.某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费.若乘客在打车后付费42元,则该乘客乘坐出租车行驶了 km.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.一次函数的自变量x的取值范围是,相应函数值的取值范围是,求这个函数的解析式.
20.如图,直线分别与x轴、y轴交于点,.直线分别与x轴、y轴交于点,,与直线交于点E.求四边形的面积.
21.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10﹣3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.
当成人按规定剂量服药后,
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.如图,在平面直角坐标系中,直线分别与轴、轴交于点、,且与直线交于点.
(1)求出、、的坐标;
(2)直接写出关于的不等式的解集;
24.文具店打算用5000元(全部用完)购进A、B两种类型的计算器进行零售,进价和零售价如下表所示:
类型 进价(元/个) 零售价(元/个)
A型计算器 50 80
B型计算器 25 45
若购进A类型的计算器x个,B类型的计算器y个,请解决下列问题.
(1)求y与x之间的函数表达式;
(2)若A、B两种类型的计算器的进货总数不超过150个,请问文具店如何进货,才能使两种计算器全部卖完后能获得最大利润?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:①当时,y随x的增大而增大,则有:
当;当时,,
把它们代入中可得:
,
∴,
∴函数解析式为.
②当时则随x的增大而减小,则有:
当时,;当时,,
把它们代入中可得
,
∴,
∴函数解析式为.
综上:函数解析式为,或.
20.解:设直线 的函数表达式为 ,
将点 , 代入得:
,解得: ,
∴直线 的函数表达式为 ,
设直线 的函数表达式为 ,
将点 , 代入得:
,解得: ,
∴直线 的函数表达式为 ,
联立得 ,解得: ,
∴ ,
∴
.
21.解:(1)当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x>2时,设y=k2x+b,
把(2,6),(10,3)代入上式,
得k2=﹣,b=.
∴x≥2时,y=﹣x+.
(2)把y=4代入y=3x,得x1=,
把y=4代入y=﹣x+,得x2=.
则x2﹣x1=6小时.
答:这个有效时间为6小时.
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.(1)解:∵直线分别与轴、轴交于点、,
∴当时,,
∴点;
当时,,解得:,
∴点;
∵直线与直线交于点,
∴,
解得:,
把代入,得,
∴点.
(2)解:∵当时,直线在直线的上方,交点为,
∴,
∴不等式的解集为:.
24.(1)解:根据题意,得,∴y关于x的函数表达式为;
(2)解:设获得的总利润为w元,根据题意,得.又∵A、B两种类型的计算器的进货总数不超过150个,∴ ,解得,∴在函数中,w随x的增大而减小,∴当时,w取最大值, ,此时.答:当A类型的计算器购进50个,B类型的计算器购进100个时,能获得最大的利润.
数学试卷 第19页(共22页) 数学试卷 第20页(共22页)
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.一本笔记本5元,买本共付元,则5和分别是( )
A.常量,常量 B.变量,变量 C.常量,变量 D.变量,常量
2.正比例函数的图象经过的象限是( )
A.第一、三象限 B.第二、四象限 C.第三、四象限 D.第一、二象限
3.已知正比例函数,若y随x的增大而减小,则k的取值范围是( )
A. B. C. D.
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.如图,一次函数的图像经过A、B两点,则关于x的不等式的解集是( )
A. B. C. D.
7.已知一次函数和的图象都经过点,且与轴分别交于两点,那么的面积是( )
A.2 B.3 C.4 D.6
8.根据图象,可得关于x的不等式的解集是( )
A. B. C. D.
9.一次函数y1=ax+b与y2=cx+d的图像如图所示,下列结论中正确的有( )
①对于函数y=ax+b来说,y随x的增大而减小②函数y=ax+d的图像不经过第一象限③④
A.1个 B.2个 C.3个 D.4个
10.如图是甲、乙两家商店销售同一种产品的销售价 (元)关于销售量 (件)的函数图象.给出下列说法,其中说法不正确的是( )
A.售2件时,甲、乙两家的售价相同 B.买1件时,买乙家的合算
C.买3件时,买甲家的合算 D.乙家的1件售价约为3元
二、填空题(每题3分,共30分)
11.点、是一次函数图象上的两个点,则 .
12.若一次函数的图像经过点,则不等式的解集为_________.
13.如果一次函数、为常数,的图像过点,且经过第一、二、三象限,那么当时,的取值范围是_________.
14.某一次函数的图象经过点(﹣1,2),且函数y的值随自变量x的增大而减小,请写出一个符合上述条件的函数关系式: .
15.若一次函数y=(1﹣2k)x+k的图象经过第一、二、三象限,则k的取值范围是 .
16.将函数y=2x的图象l1向上平移3个单位得到直线l2,则直线l2与坐标轴围成的三角形面积为 .
17.如图,在平面直角坐标系中,直线交x轴于点A,交y轴于点B,在第一象限内有一点,当时,m的值为_______.
18.某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费.若乘客在打车后付费42元,则该乘客乘坐出租车行驶了 km.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.一次函数的自变量x的取值范围是,相应函数值的取值范围是,求这个函数的解析式.
20.如图,直线分别与x轴、y轴交于点,.直线分别与x轴、y轴交于点,,与直线交于点E.求四边形的面积.
21.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=10﹣3毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量y(微克),随时间x(小时)的变化如图所示.
当成人按规定剂量服药后,
(1)分别求出x≤2和x≥2时,y与x之间的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.如图,在平面直角坐标系中,直线分别与轴、轴交于点、,且与直线交于点.
(1)求出、、的坐标;
(2)直接写出关于的不等式的解集;
24.文具店打算用5000元(全部用完)购进A、B两种类型的计算器进行零售,进价和零售价如下表所示:
类型 进价(元/个) 零售价(元/个)
A型计算器 50 80
B型计算器 25 45
若购进A类型的计算器x个,B类型的计算器y个,请解决下列问题.
(1)求y与x之间的函数表达式;
(2)若A、B两种类型的计算器的进货总数不超过150个,请问文具店如何进货,才能使两种计算器全部卖完后能获得最大利润?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:①当时,y随x的增大而增大,则有:
当;当时,,
把它们代入中可得:
,
∴,
∴函数解析式为.
②当时则随x的增大而减小,则有:
当时,;当时,,
把它们代入中可得
,
∴,
∴函数解析式为.
综上:函数解析式为,或.
20.解:设直线 的函数表达式为 ,
将点 , 代入得:
,解得: ,
∴直线 的函数表达式为 ,
设直线 的函数表达式为 ,
将点 , 代入得:
,解得: ,
∴直线 的函数表达式为 ,
联立得 ,解得: ,
∴ ,
∴
.
21.解:(1)当x≤2时,设y=k1x,
把(2,6)代入上式,得k1=3,
∴x≤2时,y=3x;
当x>2时,设y=k2x+b,
把(2,6),(10,3)代入上式,
得k2=﹣,b=.
∴x≥2时,y=﹣x+.
(2)把y=4代入y=3x,得x1=,
把y=4代入y=﹣x+,得x2=.
则x2﹣x1=6小时.
答:这个有效时间为6小时.
22.①当0
②2.4元;6.4元
23.(1)解:∵直线分别与轴、轴交于点、,
∴当时,,
∴点;
当时,,解得:,
∴点;
∵直线与直线交于点,
∴,
解得:,
把代入,得,
∴点.
(2)解:∵当时,直线在直线的上方,交点为,
∴,
∴不等式的解集为:.
24.(1)解:根据题意,得,∴y关于x的函数表达式为;
(2)解:设获得的总利润为w元,根据题意,得.又∵A、B两种类型的计算器的进货总数不超过150个,∴ ,解得,∴在函数中,w随x的增大而减小,∴当时,w取最大值, ,此时.答:当A类型的计算器购进50个,B类型的计算器购进100个时,能获得最大的利润.
数学试卷 第19页(共22页) 数学试卷 第20页(共22页)
