1.2.2同角三角函数的基本关系
文档属性
| 名称 | 1.2.2同角三角函数的基本关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 565.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-09 00:00:00 | ||
图片预览











文档简介
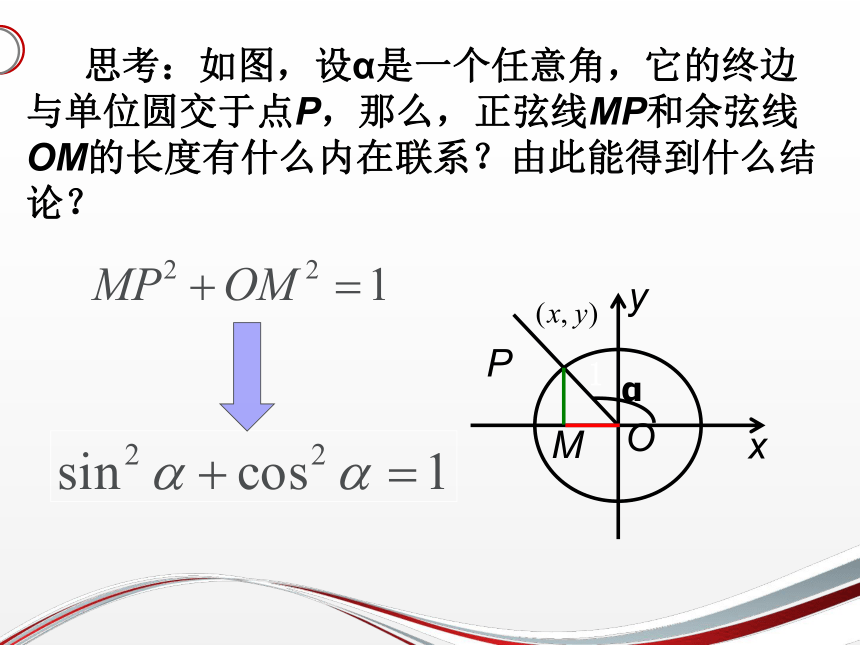
课件40张PPT。1.任意角的正弦、余弦、正切函数分别是如何定义的?P(x,y)A(1,0)复习引入2.在单位圆中,任意角的正弦、余弦、正切函数线分别是什么? 复习引入图1 三角函数是以单位圆上点的坐标来定义的,你能从圆的几何性质出发,讨论一下同一个角的不同三角函数之间的关系吗?1.2.2 同角三角函数基本关系计算&观察猜想:证明:方法二:问题 当角 的终边在坐标轴上时,关系式是否还成立?对于任意角 都有结论:平方关系 当角 的终边在 坐标轴上时,当角 的终边在 坐标轴上时,注意:① 能写成 吗?
②“同角”是什么含义?
(不能)(一是“角相等”,二是对“任意一个角”)2.已知则cos α-sin α的值等于( )Bcos2α-2sin αcos α+sin2α=1-2sin αcos α∴cos α-sin α=全优11页基础夯实1.设角A是△ABC的一个内角且则△ABC的形状是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定C平方,得sin2A+2sin A·cos A+cos2A=∴2sin Acos A=又0<A<π,则sin A>0,∴cos A<0,即A为钝角.∴△ABC为钝角三角形.全优85页限时规范训练4.若sin α+sin2α=1,则cos2α+cos4α的值等于( )A.0 B.1 C.2 D.3B【解析】由已知,得sin α=1-sin2α=cos2α,∴cos2α+cos4α=sin α+sin2α=1.全优11页基础夯实cos 20°-sin 20°【解析】∵1-2sin 20°cos 20°
=(sin 20°-cos 20°)2,又sin 20°练习:课本20页 1,4解:解:练习:课本20页 2提示:注意“1”的转化!4.已知tan α=3,则sin2α+2sin α·cos α之值为________.【解析】∵tan α=3,∴sin2α+2sin αcos α=全优84页限时规范训练解析:由得tan α=3.于是全优12页典例剖析4.若tan α=2,则A全优13页基础夯实∴原式成立三角函数恒等式证明的一般方法(2)证明原等式的等价关系注:要注意两边都有意义的条件下才恒等(1)从一边开始证明它等于另一边(由繁到简)(3)证明左、右两边等于同一式子1.若【解析】∵sin2x+cos2x=1,则1-sin2x=cos2x,全优12页变式训练练习:课本20页 5练习:课本22页 13(4)【例3】 求证:【证明】左边==右边,所以原等式成立.全优10页典例剖析8.证明恒等式【证明】左边==右边.所以原等式成立.全优11页能力提高3.求证:【证明】左边==右边.所以原等式成立.全优10页变式训练-8【解析】全优85页限时规范训练
②“同角”是什么含义?
(不能)(一是“角相等”,二是对“任意一个角”)2.已知则cos α-sin α的值等于( )Bcos2α-2sin αcos α+sin2α=1-2sin αcos α∴cos α-sin α=全优11页基础夯实1.设角A是△ABC的一个内角且则△ABC的形状是( )A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定C平方,得sin2A+2sin A·cos A+cos2A=∴2sin Acos A=又0<A<π,则sin A>0,∴cos A<0,即A为钝角.∴△ABC为钝角三角形.全优85页限时规范训练4.若sin α+sin2α=1,则cos2α+cos4α的值等于( )A.0 B.1 C.2 D.3B【解析】由已知,得sin α=1-sin2α=cos2α,∴cos2α+cos4α=sin α+sin2α=1.全优11页基础夯实cos 20°-sin 20°【解析】∵1-2sin 20°cos 20°
=(sin 20°-cos 20°)2,又sin 20°
