初中数学人教版八年级下册16.1二次根式教学设计(表格式)
文档属性
| 名称 | 初中数学人教版八年级下册16.1二次根式教学设计(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 00:00:00 | ||
图片预览

文档简介
《二次根式》教学设计
一、教学目标
1.理解二次根式的概念,
2.理解二次根式的本质是算数平方根.
3.会在简单情况下求根号内所含字母的取值范围;
4.会求含字母的二次根式的值.
二.教学重点与难点
教学重点: 二次根式的概念。
教学难点:二次根式的概念以及二次根式根号内字母的取值范围的确定。
三、教法和学情分析
对于二次根式的学习,不仅可以使学生对于初中代数式知识的认知趋于完整、系统,换句话说,学习二次根式的概念是帮助学生对代数式形成整体结构化认知的良好时机。因此在二次根式概念教学引入环节上要细细斟酌,从学生的学情出发确定教学方法。
对“二次根式”的编排在八年级上册开篇,意味着要面对学生可能的知识遗忘。因此,对于学生而言从代数式已有知识框架入手可能会遇到较大的障碍,而从实数运算——数的开平方这一知识点入手显得更简便及易理解,但是这样也意味着学生对知识遗忘的淡漠。而八年级学生在思维方式上已具有一定的抽象思维能力,也具有接受挑战的能力。基于上述对教材及学生状态的分析,我认为要以代数式已有知识框架为入口,以代数式的进一步划分为路径引入二次根式概念是可行的,且对于学生的学习与发展是有帮助的。
四、教学过程
(一)图形呈现,激发兴趣
师生活动 设计意图
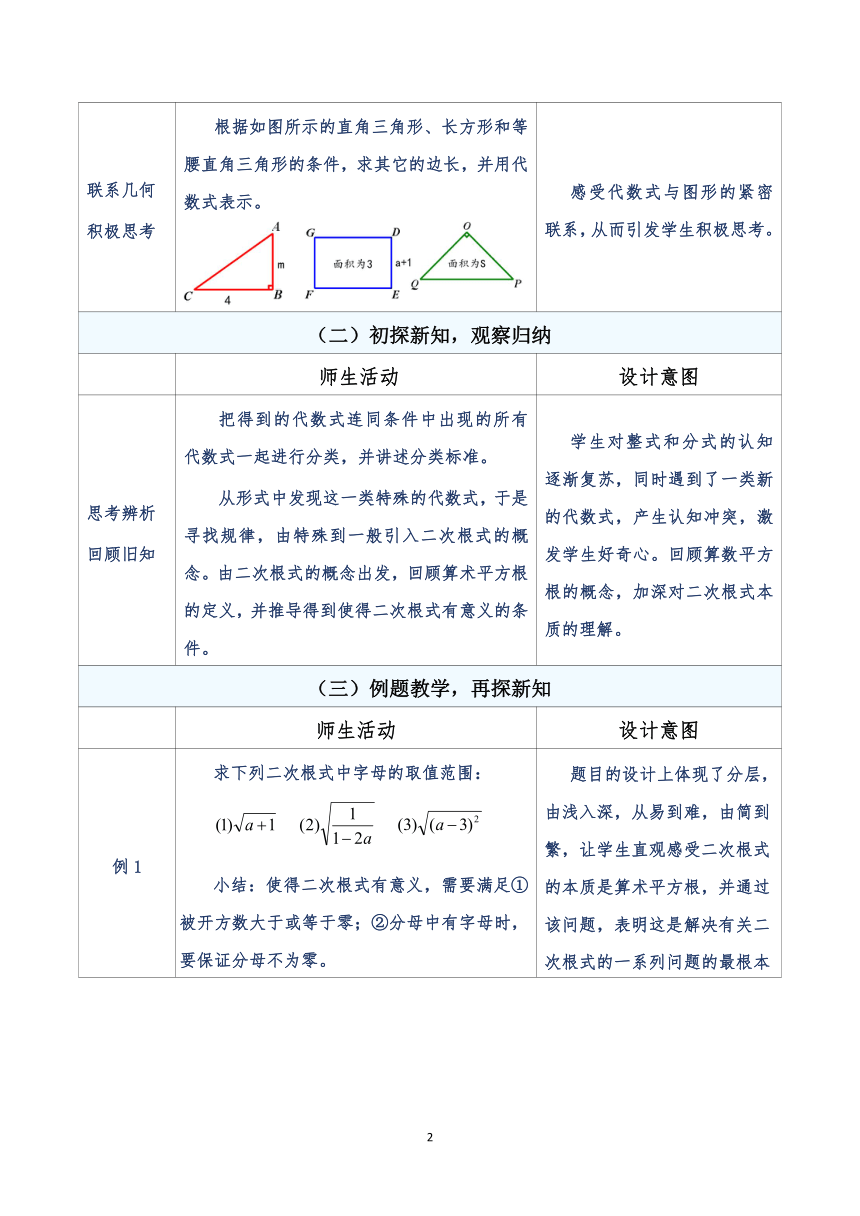
联系几何 积极思考 根据如图所示的直角三角形、长方形和等腰直角三角形的条件,求其它的边长,并用代数式表示。 感受代数式与图形的紧密联系,从而引发学生积极思考。
(二)初探新知,观察归纳
师生活动 设计意图
思考辨析 回顾旧知 把得到的代数式连同条件中出现的所有代数式一起进行分类,并讲述分类标准。 从形式中发现这一类特殊的代数式,于是寻找规律,由特殊到一般引入二次根式的概念。由二次根式的概念出发,回顾算术平方根的定义,并推导得到使得二次根式有意义的条件。 学生对整式和分式的认知逐渐复苏,同时遇到了一类新的代数式,产生认知冲突,激发学生好奇心。回顾算数平方根的概念,加深对二次根式本质的理解。
(三)例题教学,再探新知
师生活动 设计意图
例1 求下列二次根式中字母的取值范围: 小结:使得二次根式有意义,需要满足①被开方数大于或等于零;②分母中有字母时,要保证分母不为零。 题目的设计上体现了分层,由浅入深,从易到难,由简到繁,让学生直观感受二次根式的本质是算术平方根,并通过该问题,表明这是解决有关二次根式的一系列问题的最根本的依据。其中,几道易错题和较难题还设计了变式,让学生可以考虑多种情况。
练习 要使得下列二次根式有意义,求各字母的取值范围.
例2 在平面 当x= - 4时,求二次根式的值. 变式:当x分别取,时,求上述二次根式的值. 该题反映了含字母二次根式与二次根式的值在概念上的联系与区别。与学生已有的代数式的值的概念作比较.点明二次根式的值也是一种代数式的值,求值的方法也与其他代数式求值的方法相同
(四)课内小结,归纳梳理
师生活动 设计意图
课堂小结 回顾所学 二次根式的概念; 根号内字母的取值范围; 二次根式的值. (学习二次根式的意义) 小结源于知识又高于知识——回顾二次根式出现的场景以及概念上需要注意的地方。既是对知识的总结,方法的提炼,也是对学生情感的激励,让学生感受到数学的实用和有趣。
(五)课后习题,延伸拓展
师生活动 设计意图
Challenge1 x是怎样的实数时,式子在实数范围内有意义? 变式:已知,则 . 设置了三道不同形式与二次根式相关的习题,一方面,引起了学生的兴趣和面对挑战的斗志,另一方面,从不同题型上加深学生对二次根式的理解。
Challenge2 如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为6米,地面固定点C到帐篷支撑竿底部B的距离为a米. 用二次根式表示帐篷支撑竿的高AB. (2)若a=5,则帐篷支撑竿的高是多少
Challenge3 若是一个整数,求自然数的值.
五、作业布置:作业本1.1二次根式
六、板书设计
一、教学目标
1.理解二次根式的概念,
2.理解二次根式的本质是算数平方根.
3.会在简单情况下求根号内所含字母的取值范围;
4.会求含字母的二次根式的值.
二.教学重点与难点
教学重点: 二次根式的概念。
教学难点:二次根式的概念以及二次根式根号内字母的取值范围的确定。
三、教法和学情分析
对于二次根式的学习,不仅可以使学生对于初中代数式知识的认知趋于完整、系统,换句话说,学习二次根式的概念是帮助学生对代数式形成整体结构化认知的良好时机。因此在二次根式概念教学引入环节上要细细斟酌,从学生的学情出发确定教学方法。
对“二次根式”的编排在八年级上册开篇,意味着要面对学生可能的知识遗忘。因此,对于学生而言从代数式已有知识框架入手可能会遇到较大的障碍,而从实数运算——数的开平方这一知识点入手显得更简便及易理解,但是这样也意味着学生对知识遗忘的淡漠。而八年级学生在思维方式上已具有一定的抽象思维能力,也具有接受挑战的能力。基于上述对教材及学生状态的分析,我认为要以代数式已有知识框架为入口,以代数式的进一步划分为路径引入二次根式概念是可行的,且对于学生的学习与发展是有帮助的。
四、教学过程
(一)图形呈现,激发兴趣
师生活动 设计意图
联系几何 积极思考 根据如图所示的直角三角形、长方形和等腰直角三角形的条件,求其它的边长,并用代数式表示。 感受代数式与图形的紧密联系,从而引发学生积极思考。
(二)初探新知,观察归纳
师生活动 设计意图
思考辨析 回顾旧知 把得到的代数式连同条件中出现的所有代数式一起进行分类,并讲述分类标准。 从形式中发现这一类特殊的代数式,于是寻找规律,由特殊到一般引入二次根式的概念。由二次根式的概念出发,回顾算术平方根的定义,并推导得到使得二次根式有意义的条件。 学生对整式和分式的认知逐渐复苏,同时遇到了一类新的代数式,产生认知冲突,激发学生好奇心。回顾算数平方根的概念,加深对二次根式本质的理解。
(三)例题教学,再探新知
师生活动 设计意图
例1 求下列二次根式中字母的取值范围: 小结:使得二次根式有意义,需要满足①被开方数大于或等于零;②分母中有字母时,要保证分母不为零。 题目的设计上体现了分层,由浅入深,从易到难,由简到繁,让学生直观感受二次根式的本质是算术平方根,并通过该问题,表明这是解决有关二次根式的一系列问题的最根本的依据。其中,几道易错题和较难题还设计了变式,让学生可以考虑多种情况。
练习 要使得下列二次根式有意义,求各字母的取值范围.
例2 在平面 当x= - 4时,求二次根式的值. 变式:当x分别取,时,求上述二次根式的值. 该题反映了含字母二次根式与二次根式的值在概念上的联系与区别。与学生已有的代数式的值的概念作比较.点明二次根式的值也是一种代数式的值,求值的方法也与其他代数式求值的方法相同
(四)课内小结,归纳梳理
师生活动 设计意图
课堂小结 回顾所学 二次根式的概念; 根号内字母的取值范围; 二次根式的值. (学习二次根式的意义) 小结源于知识又高于知识——回顾二次根式出现的场景以及概念上需要注意的地方。既是对知识的总结,方法的提炼,也是对学生情感的激励,让学生感受到数学的实用和有趣。
(五)课后习题,延伸拓展
师生活动 设计意图
Challenge1 x是怎样的实数时,式子在实数范围内有意义? 变式:已知,则 . 设置了三道不同形式与二次根式相关的习题,一方面,引起了学生的兴趣和面对挑战的斗志,另一方面,从不同题型上加深学生对二次根式的理解。
Challenge2 如图,从帐篷支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若绳子的长度为6米,地面固定点C到帐篷支撑竿底部B的距离为a米. 用二次根式表示帐篷支撑竿的高AB. (2)若a=5,则帐篷支撑竿的高是多少
Challenge3 若是一个整数,求自然数的值.
五、作业布置:作业本1.1二次根式
六、板书设计
