湖南省长沙市明德中学2023-2024学年高二下学期5月阶段性考试数学试题(含答案)
文档属性
| 名称 | 湖南省长沙市明德中学2023-2024学年高二下学期5月阶段性考试数学试题(含答案) | 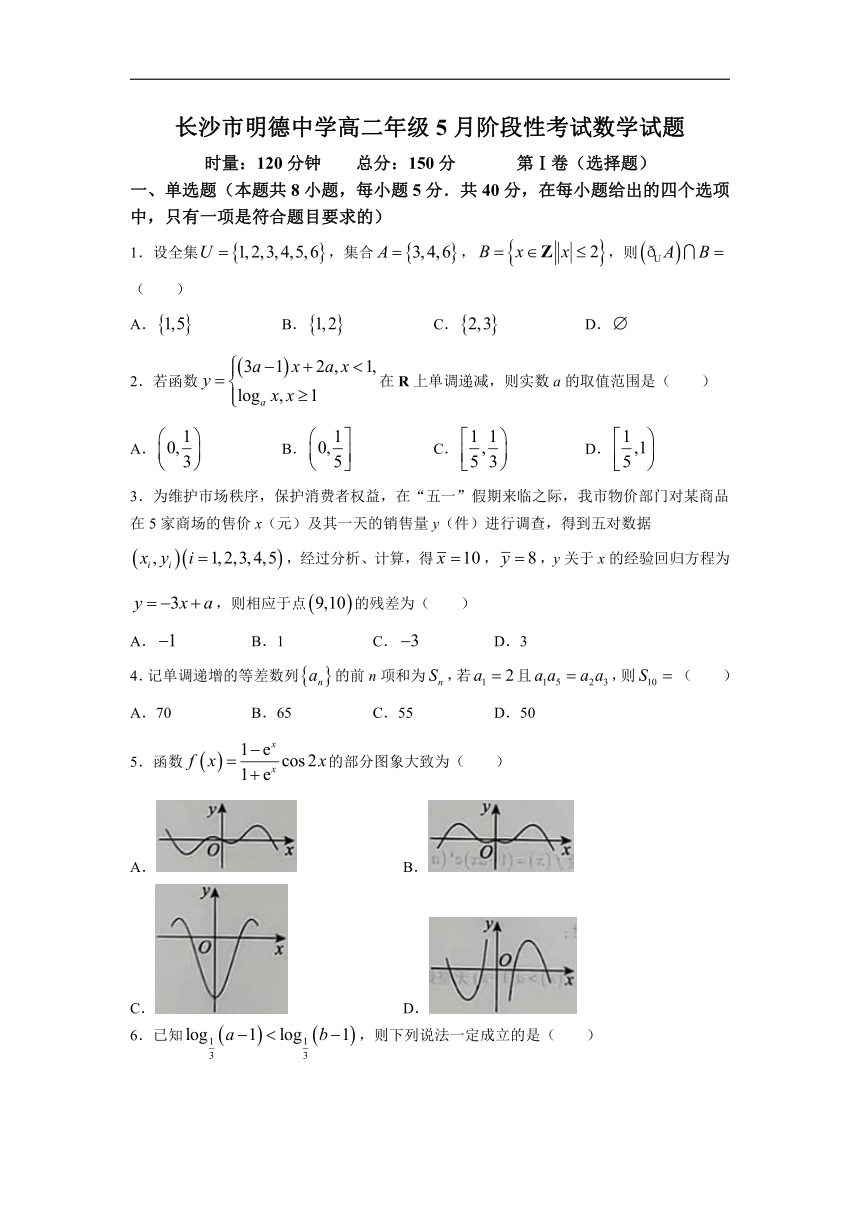 | |
| 格式 | doc | ||
| 文件大小 | 1013.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 18:46:36 | ||
图片预览





文档简介
长沙市明德中学高二年级5月阶段性考试数学试题
时量:120分钟 总分:150分 第Ⅰ卷(选择题)
一、单选题(本题共8小题,每小题5分.共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集,集合,,则( )
A. B. C. D.
2.若函数在R上单调递减,则实数a的取值范围是( )
A. B. C. D.
3.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,我市物价部门对某商品在5家商场的售价x(元)及其一天的销售量y(件)进行调查,得到五对数据,经过分析、计算,得,,y关于x的经验回归方程为,则相应于点的残差为( )
A. B.1 C. D.3
4.记单调递增的等差数列的前n项和为,若且,则 ( )
A.70 B.65 C.55 D.50
5.函数的部分图象大致为( )
A. B.
C. D.
6.已知,则下列说法一定成立的是( )
A. B.
C. D.若,则点C在线段AB上
7.平面向量,,,且与的夹角等于与的夹角,则m=( )
A. B. C.1 D.2
8.已知函数是定义域为R且周期为4的奇函数,当时,,,则下列结论错误的是( )
A. B.函数的图象关于对称
C.的最大值为 D.函数有8个零点
二、多选题(本题共3小题,每小题6分,共18分.错选0分,少选则按正确选项的比值计分)
9.下列选项正确的是( )
A.命题“,”的否定是,
B.满足的集合M的个数为4
C.已知,,则
D.已知指数函数 (其)的图象过点,则
10.已知函数的最小正周期大于,若曲线关于点中心对称,则下列说法正确的是( )
A. B.是偶函数
C.是函数的一个极值点 D.在单调递增
11.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设a,b,m()为整数,若a和b被m除得的余数相同,则称a和b对模m同余,记为.若,,则b的值不可能的是( )
A.2018 B.2020 C.2022 D.2024
第Ⅱ卷(非选择题)
三、填空题(本题共3小题,每小题5分,共15分)
12.若实数,且,则的最小值为______.
13.已知,,,则a,b,c的大小关系是______(用“>”连接)
14.某零食生产厂家准备用长为cm,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盘容积的最大值为______cm3.
四、解答题(本题共5小题,共77分.解答题应写出文字说明、证明过程或演算步骤)
15.(13分)在中,.
(1)求;
(2)若a=12,D为BC边的中点,且AD=3,求b的值.
16.(15分)某大型公司进行了新员工的招聘,共有10000人参与.招聘规则为:前两关中的每一关最多可参与两次测试,只要有一次通过,就自动进入下一关的测试,否则过关失败.若连续通过三关且第三关一次性通过,则成功竞聘,已知各关通过与否相互独立.
(1)若小李在第一关、第二关及第三关通过测试的概率分别为,,,求小李成功竞聘的概率P;
(2)统计得10000名竞聘者的得分,试估计得分在442分以上的竞聘者有多少人.(四舍五入取整)
附:若随机变量,则
,
17.(15分)如图,在三棱柱中,,,四边形是菱形.
(1)证明:;
(2)若,求二面角的正弦值.
18.(17分)欧几里得生活的时期人们就发现了椭圆有如下的光学性质:由椭圆一焦点射出的光线经椭圆内壁反射后必经过另一焦点.现有一椭圆,长轴长为4,从一个焦点F发出的一条光线经椭圆内壁上一点P反射之后恰好与x轴垂直,且.
(1)求椭圆C的标准方程;
(2)已知A为该椭圆的左顶点,若斜率为k且不经过点A的直线l与椭圆C交于M,N两点,记直线AM,AN的斜率分别为,,且满足.
①证明:直线l过定点;
②若,求k的值.
19.(17分)已知函数.
(1)讨论的单调性;
(2)若关于x的不等式无整数解,求a的取值范围.
数学参考答案:
一、单选题
题号 1 2 3 4 5 6 7 8
答案 B C A B A B D D
二、多选题:
9.BC 10.ABC 11.ACD
【详解】由,得
,
所以,
即a被10除得的余数为0,结合选项可知只有2020被10除得的余数为0,即b的值不可能的是AD.故选:ACD
三、填空题:
12.4 13. 14./
【详解】如图是四棱锥形包装盒的直观图,设,连接PO,易知PO⊥平面ABCD,
设AB、BC的中点分别为E、F,连接PE、PF,设AB=a,BC=b,PO=h,
则,因为2PE+BC=4,所以,
整理得,所以,同理,所以,
整理得,所以,所以
,
因为,所以,令,,
则,
因为,所以当时,当时,
所以在上单调递增,在上单调递减,
所以当h=1时取得最大值,即,
所以包装盒容积的最大值为cm3.故答案为:
15.(1);(2).
【详解】(1)解:因为,由正弦定理可得
,即,
,又因为,所以,
解得,又因为,所以;
(2)解:因为D为BC边的中点,a=12,所以BD=CD=6,设,
在中,由正弦定理可得,
即,解得,又因为,所以,
在中,,在中,
,BC=12,,
由余弦定理可得:,
所以,即.
16.(1) (2)228人
【详解】(1)设:第i次通过第一关测试,:第i次通过第二关测试,C:一次性通过第三关测试,因为各关通过与否相互独立,
所以
,
.
(2)由题意可知,,则,,
,
,所以得分在442分以上的竞聘者约有228人.
17.(1)证明见解析(2)
【详解】(1)三棱柱中,由可得,
因AB⊥BC,且,,则,
因,则,又四边形是菱形,则,
由,,故得,因,故.
(2)因,不妨设,则,
由余弦定理,,故得,
分别取,为x,y轴的正方向建立如图所示的空间直角坐标系.(z轴为与平面ABC垂直向上的方向),
则有,,,,,,
设平面的法向量为,则,故可取;
又因,,
设平面的法向量为,则,故可取
.
设二面角的平面角为,则,因,
故.故二面角的正弦值为.
18.(1) (2)①;②或.
【详解】(1)解:不妨设F、是椭圆的左焦点、右焦点,
则轴,又因为,2a=4,所以,即,所以,
则椭圆的标准方程为:.
(2)①证明:设直线l的方程为,,,
联立,得:,
则,,因为,所以,
即,
即,
即,
则,
即,即,则m=2k或,
当m=2k时,直线可化为,
即直线l过定点 (与左焦点重合,舍);
当时,直线可化为,
即直线l过定点;综上所述,直线l过定点;
②解:由①得,则,,
且,解得;
因为,所以,即,
即,即,即,
即,即,则或,
所以或.
19.【解析】(1),当,得,
当时,时,,单调递增,时,
,单调递减,
当时,时,,单调递减,时,
,单调递增.
当a=0时,,函数在R上单调递增,
综上可知,时,函数的单调递增区间是,单调递减区间是,
时,函数的单调递减区间是,单调递增区间是,
a=0时,函数的增区间是,无减区间.
(2)不等式,即,
设,,
设,,所以单调递增,且,,
所以存在,使,即,当时,,单调递减,
当时,,单调递增,所以,
因为,所以,
当时,,当时,,
不等式无整数解,即无整数解,
若时,不等式恒成立,有无穷多个整数解,不符合题意,
若时,即,因为函数在上单调递减,在上单调递增,
所以时,,所以无整数解,符合题意,
当时,因为,显然0,1是的两个整数解,不符合题意,
综上可知,.
时量:120分钟 总分:150分 第Ⅰ卷(选择题)
一、单选题(本题共8小题,每小题5分.共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设全集,集合,,则( )
A. B. C. D.
2.若函数在R上单调递减,则实数a的取值范围是( )
A. B. C. D.
3.为维护市场秩序,保护消费者权益,在“五一”假期来临之际,我市物价部门对某商品在5家商场的售价x(元)及其一天的销售量y(件)进行调查,得到五对数据,经过分析、计算,得,,y关于x的经验回归方程为,则相应于点的残差为( )
A. B.1 C. D.3
4.记单调递增的等差数列的前n项和为,若且,则 ( )
A.70 B.65 C.55 D.50
5.函数的部分图象大致为( )
A. B.
C. D.
6.已知,则下列说法一定成立的是( )
A. B.
C. D.若,则点C在线段AB上
7.平面向量,,,且与的夹角等于与的夹角,则m=( )
A. B. C.1 D.2
8.已知函数是定义域为R且周期为4的奇函数,当时,,,则下列结论错误的是( )
A. B.函数的图象关于对称
C.的最大值为 D.函数有8个零点
二、多选题(本题共3小题,每小题6分,共18分.错选0分,少选则按正确选项的比值计分)
9.下列选项正确的是( )
A.命题“,”的否定是,
B.满足的集合M的个数为4
C.已知,,则
D.已知指数函数 (其)的图象过点,则
10.已知函数的最小正周期大于,若曲线关于点中心对称,则下列说法正确的是( )
A. B.是偶函数
C.是函数的一个极值点 D.在单调递增
11.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设a,b,m()为整数,若a和b被m除得的余数相同,则称a和b对模m同余,记为.若,,则b的值不可能的是( )
A.2018 B.2020 C.2022 D.2024
第Ⅱ卷(非选择题)
三、填空题(本题共3小题,每小题5分,共15分)
12.若实数,且,则的最小值为______.
13.已知,,,则a,b,c的大小关系是______(用“>”连接)
14.某零食生产厂家准备用长为cm,宽为4cm的长方形纸板剪去阴影部分(如图,阴影部分是全等四边形),再将剩余部分折成一个底面为长方形的四棱锥形状的包装盒,则该包装盘容积的最大值为______cm3.
四、解答题(本题共5小题,共77分.解答题应写出文字说明、证明过程或演算步骤)
15.(13分)在中,.
(1)求;
(2)若a=12,D为BC边的中点,且AD=3,求b的值.
16.(15分)某大型公司进行了新员工的招聘,共有10000人参与.招聘规则为:前两关中的每一关最多可参与两次测试,只要有一次通过,就自动进入下一关的测试,否则过关失败.若连续通过三关且第三关一次性通过,则成功竞聘,已知各关通过与否相互独立.
(1)若小李在第一关、第二关及第三关通过测试的概率分别为,,,求小李成功竞聘的概率P;
(2)统计得10000名竞聘者的得分,试估计得分在442分以上的竞聘者有多少人.(四舍五入取整)
附:若随机变量,则
,
17.(15分)如图,在三棱柱中,,,四边形是菱形.
(1)证明:;
(2)若,求二面角的正弦值.
18.(17分)欧几里得生活的时期人们就发现了椭圆有如下的光学性质:由椭圆一焦点射出的光线经椭圆内壁反射后必经过另一焦点.现有一椭圆,长轴长为4,从一个焦点F发出的一条光线经椭圆内壁上一点P反射之后恰好与x轴垂直,且.
(1)求椭圆C的标准方程;
(2)已知A为该椭圆的左顶点,若斜率为k且不经过点A的直线l与椭圆C交于M,N两点,记直线AM,AN的斜率分别为,,且满足.
①证明:直线l过定点;
②若,求k的值.
19.(17分)已知函数.
(1)讨论的单调性;
(2)若关于x的不等式无整数解,求a的取值范围.
数学参考答案:
一、单选题
题号 1 2 3 4 5 6 7 8
答案 B C A B A B D D
二、多选题:
9.BC 10.ABC 11.ACD
【详解】由,得
,
所以,
即a被10除得的余数为0,结合选项可知只有2020被10除得的余数为0,即b的值不可能的是AD.故选:ACD
三、填空题:
12.4 13. 14./
【详解】如图是四棱锥形包装盒的直观图,设,连接PO,易知PO⊥平面ABCD,
设AB、BC的中点分别为E、F,连接PE、PF,设AB=a,BC=b,PO=h,
则,因为2PE+BC=4,所以,
整理得,所以,同理,所以,
整理得,所以,所以
,
因为,所以,令,,
则,
因为,所以当时,当时,
所以在上单调递增,在上单调递减,
所以当h=1时取得最大值,即,
所以包装盒容积的最大值为cm3.故答案为:
15.(1);(2).
【详解】(1)解:因为,由正弦定理可得
,即,
,又因为,所以,
解得,又因为,所以;
(2)解:因为D为BC边的中点,a=12,所以BD=CD=6,设,
在中,由正弦定理可得,
即,解得,又因为,所以,
在中,,在中,
,BC=12,,
由余弦定理可得:,
所以,即.
16.(1) (2)228人
【详解】(1)设:第i次通过第一关测试,:第i次通过第二关测试,C:一次性通过第三关测试,因为各关通过与否相互独立,
所以
,
.
(2)由题意可知,,则,,
,
,所以得分在442分以上的竞聘者约有228人.
17.(1)证明见解析(2)
【详解】(1)三棱柱中,由可得,
因AB⊥BC,且,,则,
因,则,又四边形是菱形,则,
由,,故得,因,故.
(2)因,不妨设,则,
由余弦定理,,故得,
分别取,为x,y轴的正方向建立如图所示的空间直角坐标系.(z轴为与平面ABC垂直向上的方向),
则有,,,,,,
设平面的法向量为,则,故可取;
又因,,
设平面的法向量为,则,故可取
.
设二面角的平面角为,则,因,
故.故二面角的正弦值为.
18.(1) (2)①;②或.
【详解】(1)解:不妨设F、是椭圆的左焦点、右焦点,
则轴,又因为,2a=4,所以,即,所以,
则椭圆的标准方程为:.
(2)①证明:设直线l的方程为,,,
联立,得:,
则,,因为,所以,
即,
即,
即,
则,
即,即,则m=2k或,
当m=2k时,直线可化为,
即直线l过定点 (与左焦点重合,舍);
当时,直线可化为,
即直线l过定点;综上所述,直线l过定点;
②解:由①得,则,,
且,解得;
因为,所以,即,
即,即,即,
即,即,则或,
所以或.
19.【解析】(1),当,得,
当时,时,,单调递增,时,
,单调递减,
当时,时,,单调递减,时,
,单调递增.
当a=0时,,函数在R上单调递增,
综上可知,时,函数的单调递增区间是,单调递减区间是,
时,函数的单调递减区间是,单调递增区间是,
a=0时,函数的增区间是,无减区间.
(2)不等式,即,
设,,
设,,所以单调递增,且,,
所以存在,使,即,当时,,单调递减,
当时,,单调递增,所以,
因为,所以,
当时,,当时,,
不等式无整数解,即无整数解,
若时,不等式恒成立,有无穷多个整数解,不符合题意,
若时,即,因为函数在上单调递减,在上单调递增,
所以时,,所以无整数解,符合题意,
当时,因为,显然0,1是的两个整数解,不符合题意,
综上可知,.
同课章节目录
