湖南省永州市第一中学2023-2024学年高一下学期5月月考数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市第一中学2023-2024学年高一下学期5月月考数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 804.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 18:49:04 | ||
图片预览



文档简介
湖南省永州市第一中学2023-2024学年高一下学期5月月考数学试卷
考生注意:
1.全卷满分150分,时量120分钟.
2.考生务必将选择题和填空题的答案填入答卷相应的答题栏内.
一、单项选择题:(本大题共8小题,每小题5分,共40分)
1.已知为虚数单位,复数,则|z|等于( )
A. B.1 C. D.5
2.若且,则与的夹角是( )
A. B. C. D.
3.某学校高一年级、高二年级、高三年级分别有学生800人、950人、1050人,学校为了调研学情,用分层抽样的方法从中抽取56人,则高三年级应该抽取的人数为( )
A.21 B.19 C.16 D.18
4.总体由编号为01,02,……,30的30个个体组成.利用所给的随机数表选取6个个体,选取的方法是从随机数表第1行的第3列开始,由左到右一次选取两个数字,则选出来的第5个个体的编号为( )
(第一行)1712 1340 3320 3826 1389 5103 7417 7637
(第二行)1304 0774 2119 3056 6218 3735 9683 5087
A.20 B.26 C.17 D.03
5.已知为的外心,,则( )
A.8 B.10 C.12 D.1
6.在空间四边形ABCD中,分别是AB,CD的中点,,则异面直线AD与BC所成角的大小为( )
A. B. C. D.
7.我国古代数学专著《九章算术》中介绍“堑堵”为:底面为直角三角形的直棱柱,如下图所示,堑堵可以分割成一个阳马(底面为长方形且有一条侧棱与底面垂直的四棱锥)和一个鳖儒(四个面都为直角三角形的四面体),已知鳖懦体积为,则阳马中AC与DF夹角的余弦值是( )
A. B. C. D.
8.在中,,与方向相同的单位向量为,则向量在上的投影向量为( )
A. B. C. D.
二、多项选择题:(本大题共3小题,每小题6分,共18分)
9.m,n是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.设是复数,则下列命题中是真命题的有( )
A.若,则; B.若,则;
C.若,则; D.若,则;
11.如图,正方体的棱长为1,点是棱上的一个动点(包含端点),则下列说法正确的是( )
A.存在点,使面 B.二面角的平面角大小为
C.的最小值是 D.到平面的距离最大值是
三、填空题:(本大题共3小题,每小题5分,共15分).
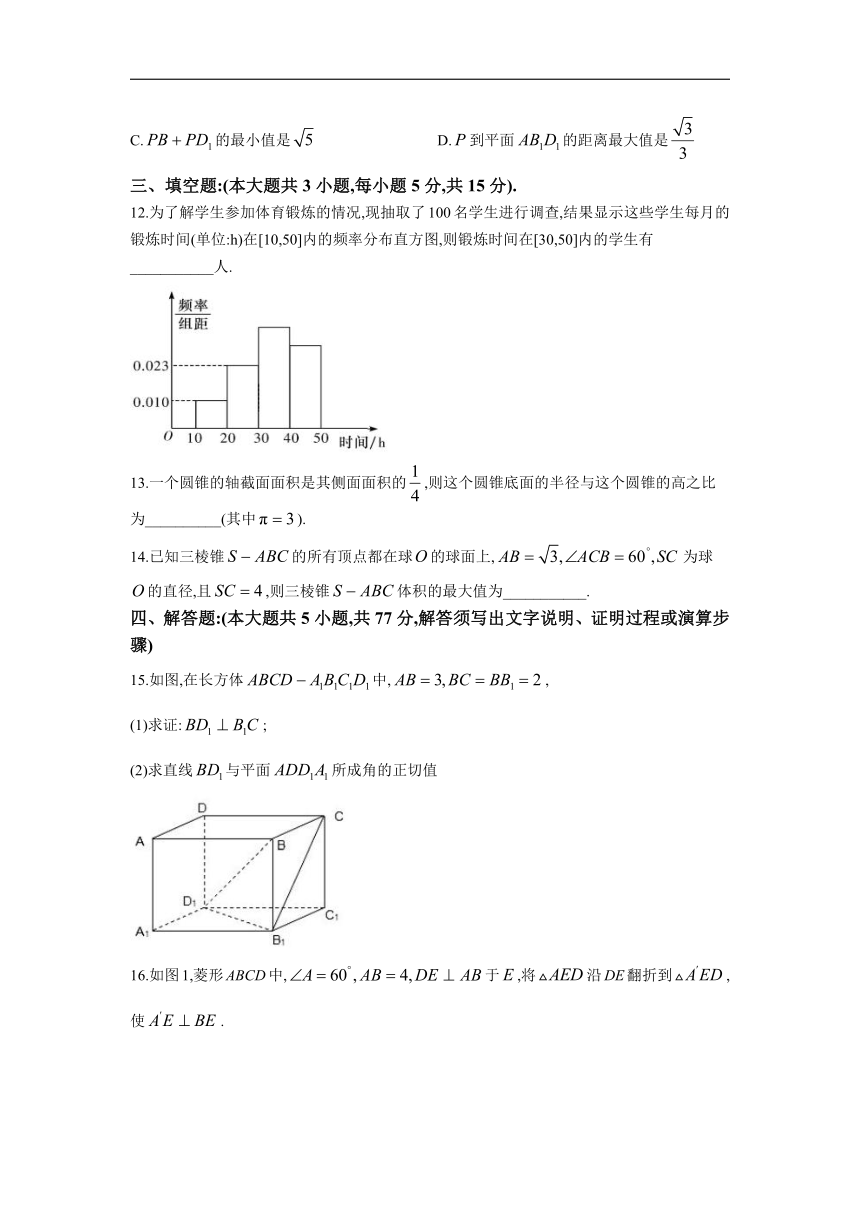
12.为了解学生参加体育锻炼的情况,现抽取了100名学生进行调查,结果显示这些学生每月的锻炼时间(单位:h)在[10,50]内的频率分布直方图,则锻炼时间在[30,50]内的学生有___________人.
13.一个圆锥的轴截面面积是其侧面面积的,则这个圆锥底面的半径与这个圆锥的高之比为__________(其中).
14.已知三棱锥的所有顶点都在球的球面上,为球的直径,且,则三棱锥体积的最大值为___________.
四、解答题:(本大题共5小题,共77分,解答须写出文字说明、证明过程或演算步骤)
15.如图,在长方体中,,
(1)求证:;
(2)求直线与平面所成角的正切值
16.如图1,菱形ABCD中,于,将沿DE翻折到,使.
(1)求三棱锥的体积;
(2)在线段上是否存在一点,使平面 若存在,求的值;若不存在,说明理由.
17.已知的内角的对边分别为若.
(1)求;
(2)若,求面积的最大值.
18.如图,在四棱锥中,底面,为PB的中点,是PC上的点。
(1)若EF//平面PAD,证明:为PC的中点
(2)求点C到平面PBD的距离
19.已知在直三棱柱中,
(1)为的中点,在线段上是否存在一点,使得平面平面,若存在,请求出CN与的比值;若不存在,说明理由;
(2)将两块形状与该直三棱柱完全相同的木料按如下图所示两种方案沿阴影面进行切割,把木料一分为二,留下体积较大的一块木料。根据你所学的知识,请判断采用哪一种方案会使留下的木料表面积较大,并说明理由。
永州一中2024年上期高一数学月考试卷参考答案)
一、单选题
1、B 2、B 3、A 4、D 5、A 6、B 7、C 8、B
二、多选题
9、ABC 10、BC 11、AC
三、填空题
12、67 13、
14.
14.由正弦定理可知,所在小圆半径为1,易知球心O到三角形ABC所在小圆的距离为,故点S到三角形ABC所在小圆的距离为,又三角形ABC面积的最大值为,故三棱锥体积的最大值为
15.(1)连接,易证,又平面,故,又,故平面,又平面,故………………………………………………………….7分
(2)连接,易证平面,故就是所求的角,又,故所求角的正切值为…………………………………………………………………………………………………………13分
16.(1)解:由题可知在菱形ABCD中,,
故,
所以在四棱锥中,,
又,所以平面EBCD,且,
连接BD,因为则分
所以.
故棱锥的体积为………………...7分
(2)设线段的中点为,线段的中点为,连接
因为点为的中点,点为的中点,所以,
又由(1)得,,所以,
所以四边形EBGF为平行四边形,故,
又平面平面,
所以平面,此时点为的中点,故.…………………………………………15分
17.(1)由题意,在中,
,即,
,可得,解得:分
(2)由题意及(1)得在中,为边AC的中点,
,即,设,则.……………………10分,所以,当且仅当时,等号成立.,当且仅当时,等号成立,的面积的最大值为..………………………………15分
18.(1)证明:因为平面平面PAD,所以平面PAD,因为点平面PBC,点平面PAD,所以可设平面平面,……………………………………3分
如图所示,又因为平面PBC,所以。因为平面平面PBC,所以,所以。又因为为PB的中点,所以为PC的中点。…………………….8分
(2)因为底面,所以,所以为等腰三角形,所以,…………………….12分
设点到平面PBD的距离为,由等体积法可得,解得,故点到平面的距离为.……17分
19.(1)由已知易证,平面,故,若要使得平面平面,即使直线平面即可,即直线直线即可,在矩形中,利用相似三角形的相似比,易得,故CN与的比值为3………………………………………………………….7分
(2)若按方案1切割易得表面积为分
若按方案2切割易得表面积为分
又,故按方案2会使留下的木料表面积较大。这个较大面积为……………………………………………………………………………………………….17分
考生注意:
1.全卷满分150分,时量120分钟.
2.考生务必将选择题和填空题的答案填入答卷相应的答题栏内.
一、单项选择题:(本大题共8小题,每小题5分,共40分)
1.已知为虚数单位,复数,则|z|等于( )
A. B.1 C. D.5
2.若且,则与的夹角是( )
A. B. C. D.
3.某学校高一年级、高二年级、高三年级分别有学生800人、950人、1050人,学校为了调研学情,用分层抽样的方法从中抽取56人,则高三年级应该抽取的人数为( )
A.21 B.19 C.16 D.18
4.总体由编号为01,02,……,30的30个个体组成.利用所给的随机数表选取6个个体,选取的方法是从随机数表第1行的第3列开始,由左到右一次选取两个数字,则选出来的第5个个体的编号为( )
(第一行)1712 1340 3320 3826 1389 5103 7417 7637
(第二行)1304 0774 2119 3056 6218 3735 9683 5087
A.20 B.26 C.17 D.03
5.已知为的外心,,则( )
A.8 B.10 C.12 D.1
6.在空间四边形ABCD中,分别是AB,CD的中点,,则异面直线AD与BC所成角的大小为( )
A. B. C. D.
7.我国古代数学专著《九章算术》中介绍“堑堵”为:底面为直角三角形的直棱柱,如下图所示,堑堵可以分割成一个阳马(底面为长方形且有一条侧棱与底面垂直的四棱锥)和一个鳖儒(四个面都为直角三角形的四面体),已知鳖懦体积为,则阳马中AC与DF夹角的余弦值是( )
A. B. C. D.
8.在中,,与方向相同的单位向量为,则向量在上的投影向量为( )
A. B. C. D.
二、多项选择题:(本大题共3小题,每小题6分,共18分)
9.m,n是两条不同的直线,是两个不同的平面,下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.设是复数,则下列命题中是真命题的有( )
A.若,则; B.若,则;
C.若,则; D.若,则;
11.如图,正方体的棱长为1,点是棱上的一个动点(包含端点),则下列说法正确的是( )
A.存在点,使面 B.二面角的平面角大小为
C.的最小值是 D.到平面的距离最大值是
三、填空题:(本大题共3小题,每小题5分,共15分).
12.为了解学生参加体育锻炼的情况,现抽取了100名学生进行调查,结果显示这些学生每月的锻炼时间(单位:h)在[10,50]内的频率分布直方图,则锻炼时间在[30,50]内的学生有___________人.
13.一个圆锥的轴截面面积是其侧面面积的,则这个圆锥底面的半径与这个圆锥的高之比为__________(其中).
14.已知三棱锥的所有顶点都在球的球面上,为球的直径,且,则三棱锥体积的最大值为___________.
四、解答题:(本大题共5小题,共77分,解答须写出文字说明、证明过程或演算步骤)
15.如图,在长方体中,,
(1)求证:;
(2)求直线与平面所成角的正切值
16.如图1,菱形ABCD中,于,将沿DE翻折到,使.
(1)求三棱锥的体积;
(2)在线段上是否存在一点,使平面 若存在,求的值;若不存在,说明理由.
17.已知的内角的对边分别为若.
(1)求;
(2)若,求面积的最大值.
18.如图,在四棱锥中,底面,为PB的中点,是PC上的点。
(1)若EF//平面PAD,证明:为PC的中点
(2)求点C到平面PBD的距离
19.已知在直三棱柱中,
(1)为的中点,在线段上是否存在一点,使得平面平面,若存在,请求出CN与的比值;若不存在,说明理由;
(2)将两块形状与该直三棱柱完全相同的木料按如下图所示两种方案沿阴影面进行切割,把木料一分为二,留下体积较大的一块木料。根据你所学的知识,请判断采用哪一种方案会使留下的木料表面积较大,并说明理由。
永州一中2024年上期高一数学月考试卷参考答案)
一、单选题
1、B 2、B 3、A 4、D 5、A 6、B 7、C 8、B
二、多选题
9、ABC 10、BC 11、AC
三、填空题
12、67 13、
14.
14.由正弦定理可知,所在小圆半径为1,易知球心O到三角形ABC所在小圆的距离为,故点S到三角形ABC所在小圆的距离为,又三角形ABC面积的最大值为,故三棱锥体积的最大值为
15.(1)连接,易证,又平面,故,又,故平面,又平面,故………………………………………………………….7分
(2)连接,易证平面,故就是所求的角,又,故所求角的正切值为…………………………………………………………………………………………………………13分
16.(1)解:由题可知在菱形ABCD中,,
故,
所以在四棱锥中,,
又,所以平面EBCD,且,
连接BD,因为则分
所以.
故棱锥的体积为………………...7分
(2)设线段的中点为,线段的中点为,连接
因为点为的中点,点为的中点,所以,
又由(1)得,,所以,
所以四边形EBGF为平行四边形,故,
又平面平面,
所以平面,此时点为的中点,故.…………………………………………15分
17.(1)由题意,在中,
,即,
,可得,解得:分
(2)由题意及(1)得在中,为边AC的中点,
,即,设,则.……………………10分,所以,当且仅当时,等号成立.,当且仅当时,等号成立,的面积的最大值为..………………………………15分
18.(1)证明:因为平面平面PAD,所以平面PAD,因为点平面PBC,点平面PAD,所以可设平面平面,……………………………………3分
如图所示,又因为平面PBC,所以。因为平面平面PBC,所以,所以。又因为为PB的中点,所以为PC的中点。…………………….8分
(2)因为底面,所以,所以为等腰三角形,所以,…………………….12分
设点到平面PBD的距离为,由等体积法可得,解得,故点到平面的距离为.……17分
19.(1)由已知易证,平面,故,若要使得平面平面,即使直线平面即可,即直线直线即可,在矩形中,利用相似三角形的相似比,易得,故CN与的比值为3………………………………………………………….7分
(2)若按方案1切割易得表面积为分
若按方案2切割易得表面积为分
又,故按方案2会使留下的木料表面积较大。这个较大面积为……………………………………………………………………………………………….17分
同课章节目录
