4.1 数列 课件(共36张PPT)
文档属性
| 名称 | 4.1 数列 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 22:44:12 | ||
图片预览











文档简介
(共36张PPT)
4.1 数列
年 级:高二年级 学 科:数学(苏教版)
本章引入
大自然这本书是用数学语言写成的。
——伽利略(意大利科学家)
本章引入
树木生长过程中枝丫的数目
果实的个数与排列方式
本章引入
观察某树木的枝丫数,第一年为1,第二年为1,第三年为2,第四年为3,第五年为5,第六年为8,第七年为13,第八年为21,第九年为34,第十年为55,第十一年为89,第十二年为144……
将它们按年份排列起来,就是下面的一列数:
1,1,2,3,5,8,13,21,34,55,89 ,144,…
——斐波那契数列
思考:你能发现这列数有什么规律吗?
本章引入
从第三个数开始,每一个数都等于前两个数的和;
相邻两个数的比值(前一个数与后一个数之比)越来越接近于某个确定的常数……
概念引入
情境一 :近年来,国产动画迅速崛起,在继承传统和推陈出新中,讲述中国故事,传播中国文化,弘扬中国精神,彰显东方审美,捍卫中国动画在世界舞台上的话语权,赢得大众一致好评,影院座无虚席。
某影院有30排座位,第一排有20个座位,从第二排起,后一排都比前一排多2个座位,那么各排的座位数依次为:
20,22,24,26,28,... ,78. ①
思考1: ①中第3,5个数的实际意义是什么?
概念引入
情境二 :自1984年起,中国开始参加夏季奥运会。经过近40年的发展,中国已成为世界体育强国之一,所获金牌总数长期稳居前三。截至2020年,我国共参加了10次夏季奥运会,各次参赛获得的金牌总数依次为:
15,5,16,16,28,32,51,38,26,38. ②
思考2:中国是在第几次参加夏季奥运会时
获得28枚金牌?
概念引入
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
思考3:①②两列数有什么共同特征?
一列数;有确定顺序。
概念引入
情境三 :
庄子曰:“一尺之捶,日取其半,万世不竭。”
意思为:一尺长的木棒,每日取其一半,永远也取不完。若将“一尺之捶”视为1 份,那么每日剩下的部分依次为:
③
概念引入
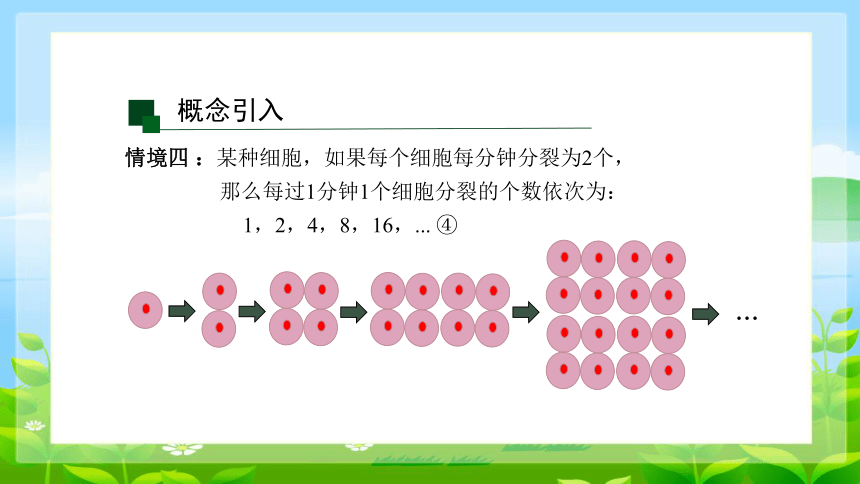
情境四 :某种细胞,如果每个细胞每分钟分裂为2个, 那么每过1分钟1个细胞分裂的个数依次为:
1,2,4,8,16,... ④
...
概念引入
情境五 :人类在 1740 年发现了一颗彗星,并推算出这颗彗星每隔83年出现一次,那么从发现那次算起,这颗彗星出现的年份依次为:
1740,1823,1906,1989,2072,... ⑤
概念引入
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
③
1,2,4,8,16,... ④
1740,1823,1906,1989,2072,... ⑤
问题1:以上几组数有什么共同特征?
一列数;按一定次序排列。
概念形成
问题2:数列的定义是什么?
按一定次序排列的一列数称为数列,
数列中的每一个数都叫做这个数列的项。
追问1:1,3,5,7是数列吗?7,5,3,1是数列吗?
这两个数列是否为同一个数列?
追问2:1,1,1,1,1,…是数列吗?
概念形成
问题3:如何用一般的符号来表示数列?
用,,,分别表示数列的第1项(或称为首项)、第2项、…,第n项,…。
数列的一般形式可以写成,,,简记为 。
记影院第n排的座位数为
例如:20,22,24,26,28,... ,78. ①
...
概念形成
问题3:如何用一般的符号来表示数列?
用,,,分别表示数列的第1项(或称为首项)、第2项、…,第n项,…。
数列的一般形式可以写成,,,简记为 。
追问:在数列中,与所表示的意义是否相同?
表示数列中的第n项(个体)
表示一个数列(整体)
概念形成
问题4:对于不同的数列,它们的项数有何特点呢?
数列 项数
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
③
1,2,4,8,16,... ④
1740,1823,1906,1989,2072,... ⑤
30
10
有穷数列:项数有限
无限
无限
无限
无穷数列:项数无限
概念辨析
问题5:数列中的各项与各项序号k(k=1,2,3,…,n,…)之间的对应关系是什么关系?
函数关系
序号
...
项
1 2 3 4 5
n
...
...
...
概念辨析
问题6:你能从函数角度来解释数列吗?
追问1:数列的自变量是什么?定义域是什么?
追问2:数列的函数值是什么?值域是什么?
数列可以看成从正整数集(或它的有限子集)到实数集的函数,当自变量按照从小到大的顺序依次取值时,所对应的一系列函数值。
反过来,对于函数,如果有意义,那么我们可以得到一个数列,,,,...
…
…
概念辨析
问题7:数列是一种特殊的函数。回顾函数的研究路径,数列的研究路径是什么?
现实背景
表示方法
性质
特殊函数
函数的研究路径:
定义
应用
概念辨析
问题7:数列是一种特殊的函数。回顾函数的研究路径,数列的研究路径是什么?
现实背景
表示方法
性质
特殊数列
数列的研究路径:
定义
应用
概念辨析
问题8:回顾函数的表示方法,数列有哪些表示方法?
函数的表示方法
列表法
解析式法
图像法
概念辨析
追问:情境一,数列:20,22,24,26,28,... ,78. ①
(1)你能将上述数列用表格、图像进行表示吗?
n 1 2 3 4 5 ... 30
20 22 24 26 28 ... 78
列表法:
图像法:
n
(2)你能表示出与n的数量关系吗?
=2n+18
通项公式
数列图像是一些离散、孤立的点
概念辨析
问题9:什么是数列的通项公式?
数列的通项公式:
数列的第n项与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子就是数列的函数解析式,叫做这个数列的通项公式。
概念辨析
问题10:通过上述研究,我们得到了数列:20,22,24,26,28,... ,78. ①的通项公式,换个角度来看,观察该数列的相邻两项,你有什么发现?
=20,
+2,
=24= +2,
=78= +2.
:
=20,
概念辨析
问题11:什么是数列的递推公式?
数列的递推公式:
一般地,如果已知一个数列的第1项(或前几项),且任一项与它的前一项(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式。
概念辨析
问题12:通项公式与递推公式有什么异同之处?
通项公式 递推公式
区别
联系 (1) 都是数列的一种表示方法;
(2) 求出数列的任意一项.
表示与n之间的关系
表示与它的前一项(或前几项)间的关系
概念辨析
问题13:斐波那契数列:1,1,2,3,5,8,13,…
(1)你能写出斐波那契数列的通项公式吗?
=1,
=1,
=2=+ ,
=8=+ .
:
=1, =1
( )
=3=+ ,
=5=+ ,
(2)你能写出斐波那契数列的递推公式吗?
概念巩固
例1:分别根据下列条件,写出数列的前5项:
(1),,,其中;
(2),,其中.
解:(1)因为,,,其中;
所以
=2+=4,
=4+=8,
=8+=16,
因此,数列的前5项依次为1,2,4,8,16.
概念巩固
例1:分别根据下列条件,写出数列的前5项:
(1),,,其中;
(2),,其中.
解:(2)因为,,其中
因此,数列的前5项依次为2, , , , .
所以
,
,
,
,
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
分析:(1)绝对值:
,,,,…
小提示
或常常用来表示正负相间的变化规律。
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
解:(1)这个数列前4项的绝对值都是分数,分子都为1,分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是:
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
小提示
或常常用来表示正负相间的变化规律。
分析:(2)
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
(2)这个数列的奇数项是0,偶数项是2,所以它的一个通项公式是:
解:(1)这个数列前4项的绝对值都是分数,分子都为1,分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是:
课堂总结
通过这节课的学习,你有哪些收获?
课堂总结
数列
定义
本质:函数。
表示方法:列表、图像、通项公式及递推公式。
按一定次序排列的一列数称为数列,
数列中的每一个数都叫做这个数列的项。
数列的一般形式可以写成,,,简记为 。
项数有限的数列叫作有穷数列,项数无限的数列叫作无穷数列.
数列可以看成从正整数集(或它的有限子集)到实数集的函数
课堂总结
从现实背景出发,
经历了数列概念的抽象过程
从特殊到一般、从具体到抽象、类比
数学抽象、数学建模、
逻辑推理、数学运算
4.1 数列
年 级:高二年级 学 科:数学(苏教版)
本章引入
大自然这本书是用数学语言写成的。
——伽利略(意大利科学家)
本章引入
树木生长过程中枝丫的数目
果实的个数与排列方式
本章引入
观察某树木的枝丫数,第一年为1,第二年为1,第三年为2,第四年为3,第五年为5,第六年为8,第七年为13,第八年为21,第九年为34,第十年为55,第十一年为89,第十二年为144……
将它们按年份排列起来,就是下面的一列数:
1,1,2,3,5,8,13,21,34,55,89 ,144,…
——斐波那契数列
思考:你能发现这列数有什么规律吗?
本章引入
从第三个数开始,每一个数都等于前两个数的和;
相邻两个数的比值(前一个数与后一个数之比)越来越接近于某个确定的常数……
概念引入
情境一 :近年来,国产动画迅速崛起,在继承传统和推陈出新中,讲述中国故事,传播中国文化,弘扬中国精神,彰显东方审美,捍卫中国动画在世界舞台上的话语权,赢得大众一致好评,影院座无虚席。
某影院有30排座位,第一排有20个座位,从第二排起,后一排都比前一排多2个座位,那么各排的座位数依次为:
20,22,24,26,28,... ,78. ①
思考1: ①中第3,5个数的实际意义是什么?
概念引入
情境二 :自1984年起,中国开始参加夏季奥运会。经过近40年的发展,中国已成为世界体育强国之一,所获金牌总数长期稳居前三。截至2020年,我国共参加了10次夏季奥运会,各次参赛获得的金牌总数依次为:
15,5,16,16,28,32,51,38,26,38. ②
思考2:中国是在第几次参加夏季奥运会时
获得28枚金牌?
概念引入
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
思考3:①②两列数有什么共同特征?
一列数;有确定顺序。
概念引入
情境三 :
庄子曰:“一尺之捶,日取其半,万世不竭。”
意思为:一尺长的木棒,每日取其一半,永远也取不完。若将“一尺之捶”视为1 份,那么每日剩下的部分依次为:
③
概念引入
情境四 :某种细胞,如果每个细胞每分钟分裂为2个, 那么每过1分钟1个细胞分裂的个数依次为:
1,2,4,8,16,... ④
...
概念引入
情境五 :人类在 1740 年发现了一颗彗星,并推算出这颗彗星每隔83年出现一次,那么从发现那次算起,这颗彗星出现的年份依次为:
1740,1823,1906,1989,2072,... ⑤
概念引入
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
③
1,2,4,8,16,... ④
1740,1823,1906,1989,2072,... ⑤
问题1:以上几组数有什么共同特征?
一列数;按一定次序排列。
概念形成
问题2:数列的定义是什么?
按一定次序排列的一列数称为数列,
数列中的每一个数都叫做这个数列的项。
追问1:1,3,5,7是数列吗?7,5,3,1是数列吗?
这两个数列是否为同一个数列?
追问2:1,1,1,1,1,…是数列吗?
概念形成
问题3:如何用一般的符号来表示数列?
用,,,分别表示数列的第1项(或称为首项)、第2项、…,第n项,…。
数列的一般形式可以写成,,,简记为 。
记影院第n排的座位数为
例如:20,22,24,26,28,... ,78. ①
...
概念形成
问题3:如何用一般的符号来表示数列?
用,,,分别表示数列的第1项(或称为首项)、第2项、…,第n项,…。
数列的一般形式可以写成,,,简记为 。
追问:在数列中,与所表示的意义是否相同?
表示数列中的第n项(个体)
表示一个数列(整体)
概念形成
问题4:对于不同的数列,它们的项数有何特点呢?
数列 项数
20,22,24,26,28,... ,78. ①
15,5,16,16,28,32,51,38,26,38. ②
③
1,2,4,8,16,... ④
1740,1823,1906,1989,2072,... ⑤
30
10
有穷数列:项数有限
无限
无限
无限
无穷数列:项数无限
概念辨析
问题5:数列中的各项与各项序号k(k=1,2,3,…,n,…)之间的对应关系是什么关系?
函数关系
序号
...
项
1 2 3 4 5
n
...
...
...
概念辨析
问题6:你能从函数角度来解释数列吗?
追问1:数列的自变量是什么?定义域是什么?
追问2:数列的函数值是什么?值域是什么?
数列可以看成从正整数集(或它的有限子集)到实数集的函数,当自变量按照从小到大的顺序依次取值时,所对应的一系列函数值。
反过来,对于函数,如果有意义,那么我们可以得到一个数列,,,,...
…
…
概念辨析
问题7:数列是一种特殊的函数。回顾函数的研究路径,数列的研究路径是什么?
现实背景
表示方法
性质
特殊函数
函数的研究路径:
定义
应用
概念辨析
问题7:数列是一种特殊的函数。回顾函数的研究路径,数列的研究路径是什么?
现实背景
表示方法
性质
特殊数列
数列的研究路径:
定义
应用
概念辨析
问题8:回顾函数的表示方法,数列有哪些表示方法?
函数的表示方法
列表法
解析式法
图像法
概念辨析
追问:情境一,数列:20,22,24,26,28,... ,78. ①
(1)你能将上述数列用表格、图像进行表示吗?
n 1 2 3 4 5 ... 30
20 22 24 26 28 ... 78
列表法:
图像法:
n
(2)你能表示出与n的数量关系吗?
=2n+18
通项公式
数列图像是一些离散、孤立的点
概念辨析
问题9:什么是数列的通项公式?
数列的通项公式:
数列的第n项与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子就是数列的函数解析式,叫做这个数列的通项公式。
概念辨析
问题10:通过上述研究,我们得到了数列:20,22,24,26,28,... ,78. ①的通项公式,换个角度来看,观察该数列的相邻两项,你有什么发现?
=20,
+2,
=24= +2,
=78= +2.
:
=20,
概念辨析
问题11:什么是数列的递推公式?
数列的递推公式:
一般地,如果已知一个数列的第1项(或前几项),且任一项与它的前一项(或前几项)间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的递推公式。
概念辨析
问题12:通项公式与递推公式有什么异同之处?
通项公式 递推公式
区别
联系 (1) 都是数列的一种表示方法;
(2) 求出数列的任意一项.
表示与n之间的关系
表示与它的前一项(或前几项)间的关系
概念辨析
问题13:斐波那契数列:1,1,2,3,5,8,13,…
(1)你能写出斐波那契数列的通项公式吗?
=1,
=1,
=2=+ ,
=8=+ .
:
=1, =1
( )
=3=+ ,
=5=+ ,
(2)你能写出斐波那契数列的递推公式吗?
概念巩固
例1:分别根据下列条件,写出数列的前5项:
(1),,,其中;
(2),,其中.
解:(1)因为,,,其中;
所以
=2+=4,
=4+=8,
=8+=16,
因此,数列的前5项依次为1,2,4,8,16.
概念巩固
例1:分别根据下列条件,写出数列的前5项:
(1),,,其中;
(2),,其中.
解:(2)因为,,其中
因此,数列的前5项依次为2, , , , .
所以
,
,
,
,
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
分析:(1)绝对值:
,,,,…
小提示
或常常用来表示正负相间的变化规律。
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
解:(1)这个数列前4项的绝对值都是分数,分子都为1,分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是:
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
小提示
或常常用来表示正负相间的变化规律。
分析:(2)
概念巩固
例2:你能根据数列的前4项,写出数列的一个通项公式吗?
(1),-,,,…
(2)0,2,0,2,…
(2)这个数列的奇数项是0,偶数项是2,所以它的一个通项公式是:
解:(1)这个数列前4项的绝对值都是分数,分子都为1,分母都等于序号与序号加1的积,且奇数项为正,偶数项为负,所以它的一个通项公式是:
课堂总结
通过这节课的学习,你有哪些收获?
课堂总结
数列
定义
本质:函数。
表示方法:列表、图像、通项公式及递推公式。
按一定次序排列的一列数称为数列,
数列中的每一个数都叫做这个数列的项。
数列的一般形式可以写成,,,简记为 。
项数有限的数列叫作有穷数列,项数无限的数列叫作无穷数列.
数列可以看成从正整数集(或它的有限子集)到实数集的函数
课堂总结
从现实背景出发,
经历了数列概念的抽象过程
从特殊到一般、从具体到抽象、类比
数学抽象、数学建模、
逻辑推理、数学运算
