陕西省西安市陕西师范大学附属中学2024届高三下学期第十次模考数学(理)试卷(含答案)
文档属性
| 名称 | 陕西省西安市陕西师范大学附属中学2024届高三下学期第十次模考数学(理)试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 07:42:06 | ||
图片预览




文档简介
陕西师大附中高2024届高三年级
第十次模考数学(理科)试题
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,则( )
A. B. C. D.
2.定义运算,则满足(i为虚数单位)的复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知菱形的边长为1,,则( )
A. B. C. D.
4.黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器.该龙纹盘敞口,弧壁,广底,圈足.器内施白釉,外壁以黄釉为地,刻云龙纹并填绿彩,美不胜收.黄地绿彩云龙纹盘可近似看作是圆台和圆柱的组合体,其口径,足径,高,其中底部圆柱高,则黄地绿彩云龙纹盘的侧面积约为( )(附:的值取3,)
A. B. C. D.
5.已知函数是奇函数,则( )
A. B. C. D.
6.2024年中国足球乙级联赛陕西联合的主场火爆,一票难求,主办方设定了三种不同的票价分别对应球场三个不同的区域,五位球迷相约看球赛,则五人中恰有三人在同一区域的不同座位方式共有( )
A.30种 B.60种 C.120种 D.240种
7.设是坐标原点,在区域内随机取一点,记该点为,则直线的倾斜角不大于的概率为( )
A. B. C. D.
8.一个几何体的三视图如图所示,如果该几何体的顶点都在球的球面上,那么球的表面积是( )
A. B. C. D.
9.在平面直角坐标系中,圆的方程为,若直线上存在一点,使过点所作的圆的两条切线相互垂直,则实数的值不可能是( )
A.-1 B. C. D.
10.2024年1月九省联考的数学试卷出现新结构,其中多选题计分标准如下:①本题共3小题,每小题6分,满分18分;②每道小题的四个选项中有两个或三个正确选项,全部选对得6分,有选错的得0分;③部分选对得部分分(若某小题正确选项为两个,漏选一个正确选项得3分;若某小题正确选项为三个,漏选一个正确选项得4分,漏选两个正确选项得2分).已知在某次新结构数学试题的考试中,小明同学三个多选题中第一小题确定得满分,第二小题随机地选了两个选项,第三小题随机地选了一个选项,则小明同学多选题所有可能总得分(相同总分只记录一次)的中位数为( )
A.9 B.10 C.11 D.12
11.已知抛物线的焦点为,准线为,过且斜率为的直线与交于两点,为的中点,且于点的垂直平分线交轴于点,四边形的面积为,( )
A. B. C. D.
12.已知函数,对,有,,且函数在上单调递增,则的值为( )
A.3或9 B.3 C.9 D.6
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷中相应的横线上.)
13.已知双曲线的左右焦点分别为,曲线上的点满足,,则双曲线的离心率为______.
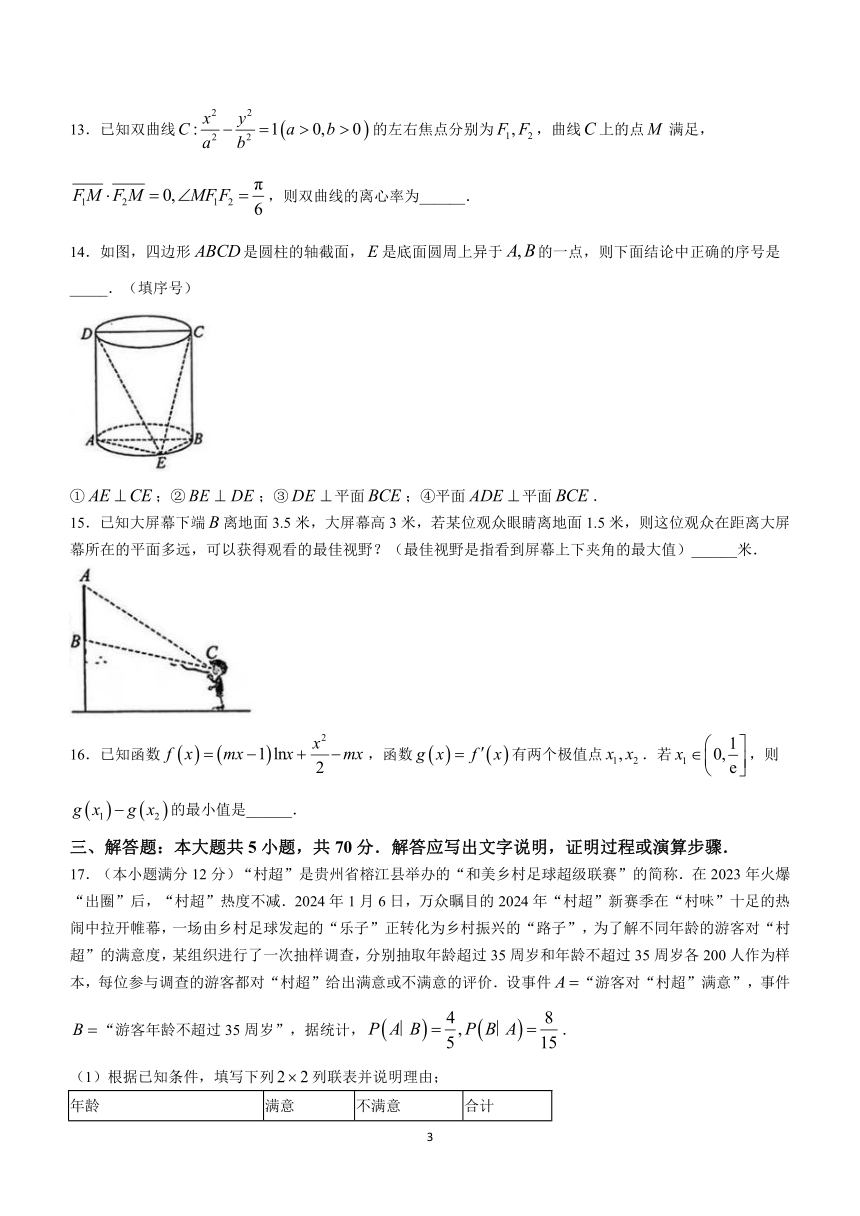
14.如图,四边形是圆柱的轴截面,是底面圆周上异于的一点,则下面结论中正确的序号是_____.(填序号)
①;②;③平面;④平面平面.
15.已知大屏幕下端离地面3.5米,大屏幕高3米,若某位观众眼睛离地面1.5米,则这位观众在距离大屏幕所在的平面多远,可以获得观看的最佳视野?(最佳视野是指看到屏幕上下夹角的最大值)______米.
16.已知函数,函数有两个极值点.若,则的最小值是______.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)“村超”是贵州省榕江县举办的“和美乡村足球超级联赛”的简称.在2023年火爆“出圈”后,“村超”热度不减.2024年1月6日,万众瞩目的2024年“村超”新赛季在“村味”十足的热闹中拉开帷幕,一场由乡村足球发起的“乐子”正转化为乡村振兴的“路子”,为了解不同年龄的游客对“村超”的满意度,某组织进行了一次抽样调查,分别抽取年龄超过35周岁和年龄不超过35周岁各200人作为样本,每位参与调查的游客都对“村超”给出满意或不满意的评价.设事件“游客对“村超”满意”,事件“游客年龄不超过35周岁”,据统计,.
(1)根据已知条件,填写下列列联表并说明理由;
年龄 满意 不满意 合计
年龄不超过35周岁
年龄超过35周岁
合计
(2)由(1)中列联表数据,分析是否有的把握认为游客对“村超”的满意度与年龄有关联?附:.
参考数据:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
18.(本小题满分12分)如图,已知正方体的棱长为2,E,F分别为的中点.
(1)已知点满足,求证B,E,G,F四点共面;
(2)求平面BA1C1与平面BEF所成的锐二面角的余弦值.
19.(本小题满分12分)数列的前项的最大值记为,即;前项的最小值记为,即,令,并将数列称为的“生成数列”.
(1)设数列的“生成数列”为,求证:;
(2)若,求其生成数列的前项和.
20.(本小题满分12分)已知椭圆的离心率为,其左右焦点分别为下顶点为,右顶点为的面积为.
(1)求椭圆的方程.
(2)设不过原点的直线交椭圆于M,N两点,且直线OM,MN,ON的斜率依次成等比数列,求面积的取值范围.
21.(本小题满分12分)已知函数,曲线在点处的切线与轴平行或重合.
(1)求的值;
(2)若对恒成立,求的取值范围;
(3)利用下表数据证明:.
1.010 0.990 2.182 0.458 2.204 0.454
四.选做题:请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号。
22.(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线的参数方程为,(为参数),以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.
(1)写出曲线的极坐标方程和曲线的直角坐标方程;
(2)若射线与曲线相交于点,将逆时针旋转后,与曲线相交于点,且,求的值.
23.(本小题满分10分)选修4-5:不等式选讲
已知函数的最小值为3,其中.
(1)求不等式的解集;
(2)若关于的方程有实数根,求实数的取值范围.
陕西师大附中高2024届高三年级
第十次模考数学(理科)详细答案
一、选择题:本题共12小题,每小题5分,共60分.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D B B D C A C B C A B
二、填空题:本大题共4小题,每小题5分,共20分.
题号 13 14 15 16
答案 ①②④
部分选填试题详细解答:
8.【详解】由三视图知:几何体为三棱锥,且三棱锥的一条侧棱与底面垂直,高为2,底面为等腰直角三角形,如图:平面,故平面,所以平面,在等腰直角三角形中,取O为的中点,连,则,所以为三棱锥外接球的球心,设半径为,
由题可得,所以,所以外接球的表面积.
9.【详解】由,得,则圆心,半径,因为过点所作的圆的两条切线相互垂直,所以及两切点构成边长为2的正方形,且对角线,又在直线上,则圆心到直线的距离,解得或,即,根据选项,满足条件的为B.
10.【详解】由题意得小明同学第一题得6分:
第二题选了2个选项,可能得分情况有3种,分别是得0分、4分和6分;
第二题选了1个选项,可能得分情况有3种,分别是得0分、2分和3分;
由于相同总分只记录一次,因此小明的总分情况有:6分、8分、9分、10分、12分、13分、14分、15分共8种情况,所以中位数为,
11.【详解】由题意可知,,直线的方程为.
设,由.得.
所以,所以.由,得.
如图所示,作轴于点,则.
因为,故,
,又,
故.又,得四边形为平行四边形.
所以其面积为,解得.故答案为:.
12.【详解】设函数的最小正周期为,因为函数在上单调递增,
所以,得,因此.
由知的图象关于直线对称,
由知的图象关于点对称.
①,得,
解得,故,
所以,因为的图象关于直线对称,
所以,则,
因为,所以,故,
当时,,满足在上单调递增;
②,得,
解得,故,
所以,因为的图象关于直线对称,
所以,则,因为,所以,
故,当时,,
不满足在上单调递增,故.
14.【详解】因为四边形是圆柱的轴截面,则线段是直径,都是母线.又是底面圆周上异于的一点,于是得.而平面,平面,则.因为平面,则平面,因为平面,因此得,①正确:同理,,②正确:点不在底面内,而直线在底面内,即是两条不同直线,若平面,因平面,与过一点有且只有一条直线垂直于已知平面矛盾,③不正确;因为平面,而平面,于是得平面平面,④正确.
15.【详解】如图所示:由题意知:,设,
则由于,当且仅当,即时取等号,
所以,因为,
所以当时,可以获得观看的最佳视野.
16.【详解】因为,
令,
因为有两个极值点,
所以是方程在上的两根,所以,所以,,所以
设,则
所以当时,,所以在上单调递减,
所以,即的最小值为.
由可得,,取,则设平面的一个法向量.设平面BEF的一个法向量为,由可得,,
取,则是平面的一个法向量.
所以,,
所以平面与平面所成锐二面角的余弦值为.
19.【详解】(1)由题意可知,
所以,因此,即是单调递增数列,且,
由“生成数列”的定义可得.
(2)当时,.
,又,
,当时,.
设数列的前项和为.则.
当时,
又符合上式,所以.
20.【详解】(1)依题意,
又,又,
所以,所以椭圆C的方程为.
(2)由题意可知,直线的斜率存在且不为0,故可设直线:,
,联立直线和椭圆,
化简得,
由题意可知,即,
且,
则
又直线的斜率依次成等比数列.即,
则,所以且,
设点到直线的距离为,
又
所以,
令,
显然在上为增函数,在上为减函数,所以,即,
所以故面积的取值范围为.
21.【详解】(1),所以,
由条件得,得到,又,所以.
(2)由(1)知,由得:,,由题知对恒成立,
令,因为,
当时,,又,
所以当时,恒成立,即单调递减,
所以,条件成立,
当时,,所以条件不成立.综上,的取值范围为.
(3),由(2)知在上恒成立,
当且仅当时取等号,所以,即,所以命题得证.
四.选做题:请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.
22.(本小题满分10分)选修4-4:坐标系与参数方程
【详解】(1)由曲线的参数方程为,(为参数),可得其普通方程,
由,得曲线的极坐标方程.
,由,得曲线的直角坐标方程.
(2)将代入,得.
将逆时针旋转,得的极坐标方程为,
代入曲线的极坐标方程,得.由,
得.即,
解得.因为,所以.
23.(本小题满分10分)选修4—5:不等式选讲
【详解】(1)由,
当且仅当时取等号:因为的最小值为3,所以,又,
所以.所以即,即或或解得,故不等式的解集为.
(2)由,
作出函数的图象及直线,
如图所示,其中.
因为方程有实数根,所以的图象与直线有公共点.
因为过定点,所以当直线经过点时,斜率,
即时,直线与的图像有公共点,也就是方程有实数根;
由图像知,直线的斜率小于直线的斜率时,得,
此时直线与的图像也有公共点,也就是方程有实数根.
即实数的取值范围是.
第十次模考数学(理科)试题
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知集合,则( )
A. B. C. D.
2.定义运算,则满足(i为虚数单位)的复数在复平面内对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知菱形的边长为1,,则( )
A. B. C. D.
4.黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器.该龙纹盘敞口,弧壁,广底,圈足.器内施白釉,外壁以黄釉为地,刻云龙纹并填绿彩,美不胜收.黄地绿彩云龙纹盘可近似看作是圆台和圆柱的组合体,其口径,足径,高,其中底部圆柱高,则黄地绿彩云龙纹盘的侧面积约为( )(附:的值取3,)
A. B. C. D.
5.已知函数是奇函数,则( )
A. B. C. D.
6.2024年中国足球乙级联赛陕西联合的主场火爆,一票难求,主办方设定了三种不同的票价分别对应球场三个不同的区域,五位球迷相约看球赛,则五人中恰有三人在同一区域的不同座位方式共有( )
A.30种 B.60种 C.120种 D.240种
7.设是坐标原点,在区域内随机取一点,记该点为,则直线的倾斜角不大于的概率为( )
A. B. C. D.
8.一个几何体的三视图如图所示,如果该几何体的顶点都在球的球面上,那么球的表面积是( )
A. B. C. D.
9.在平面直角坐标系中,圆的方程为,若直线上存在一点,使过点所作的圆的两条切线相互垂直,则实数的值不可能是( )
A.-1 B. C. D.
10.2024年1月九省联考的数学试卷出现新结构,其中多选题计分标准如下:①本题共3小题,每小题6分,满分18分;②每道小题的四个选项中有两个或三个正确选项,全部选对得6分,有选错的得0分;③部分选对得部分分(若某小题正确选项为两个,漏选一个正确选项得3分;若某小题正确选项为三个,漏选一个正确选项得4分,漏选两个正确选项得2分).已知在某次新结构数学试题的考试中,小明同学三个多选题中第一小题确定得满分,第二小题随机地选了两个选项,第三小题随机地选了一个选项,则小明同学多选题所有可能总得分(相同总分只记录一次)的中位数为( )
A.9 B.10 C.11 D.12
11.已知抛物线的焦点为,准线为,过且斜率为的直线与交于两点,为的中点,且于点的垂直平分线交轴于点,四边形的面积为,( )
A. B. C. D.
12.已知函数,对,有,,且函数在上单调递增,则的值为( )
A.3或9 B.3 C.9 D.6
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每小题5分,共20分,把答案填在答题卷中相应的横线上.)
13.已知双曲线的左右焦点分别为,曲线上的点满足,,则双曲线的离心率为______.
14.如图,四边形是圆柱的轴截面,是底面圆周上异于的一点,则下面结论中正确的序号是_____.(填序号)
①;②;③平面;④平面平面.
15.已知大屏幕下端离地面3.5米,大屏幕高3米,若某位观众眼睛离地面1.5米,则这位观众在距离大屏幕所在的平面多远,可以获得观看的最佳视野?(最佳视野是指看到屏幕上下夹角的最大值)______米.
16.已知函数,函数有两个极值点.若,则的最小值是______.
三、解答题:本大题共5小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(本小题满分12分)“村超”是贵州省榕江县举办的“和美乡村足球超级联赛”的简称.在2023年火爆“出圈”后,“村超”热度不减.2024年1月6日,万众瞩目的2024年“村超”新赛季在“村味”十足的热闹中拉开帷幕,一场由乡村足球发起的“乐子”正转化为乡村振兴的“路子”,为了解不同年龄的游客对“村超”的满意度,某组织进行了一次抽样调查,分别抽取年龄超过35周岁和年龄不超过35周岁各200人作为样本,每位参与调查的游客都对“村超”给出满意或不满意的评价.设事件“游客对“村超”满意”,事件“游客年龄不超过35周岁”,据统计,.
(1)根据已知条件,填写下列列联表并说明理由;
年龄 满意 不满意 合计
年龄不超过35周岁
年龄超过35周岁
合计
(2)由(1)中列联表数据,分析是否有的把握认为游客对“村超”的满意度与年龄有关联?附:.
参考数据:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
18.(本小题满分12分)如图,已知正方体的棱长为2,E,F分别为的中点.
(1)已知点满足,求证B,E,G,F四点共面;
(2)求平面BA1C1与平面BEF所成的锐二面角的余弦值.
19.(本小题满分12分)数列的前项的最大值记为,即;前项的最小值记为,即,令,并将数列称为的“生成数列”.
(1)设数列的“生成数列”为,求证:;
(2)若,求其生成数列的前项和.
20.(本小题满分12分)已知椭圆的离心率为,其左右焦点分别为下顶点为,右顶点为的面积为.
(1)求椭圆的方程.
(2)设不过原点的直线交椭圆于M,N两点,且直线OM,MN,ON的斜率依次成等比数列,求面积的取值范围.
21.(本小题满分12分)已知函数,曲线在点处的切线与轴平行或重合.
(1)求的值;
(2)若对恒成立,求的取值范围;
(3)利用下表数据证明:.
1.010 0.990 2.182 0.458 2.204 0.454
四.选做题:请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号。
22.(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线的参数方程为,(为参数),以坐标原点为极点,轴的正半轴为极轴,建立极坐标系,曲线的极坐标方程为.
(1)写出曲线的极坐标方程和曲线的直角坐标方程;
(2)若射线与曲线相交于点,将逆时针旋转后,与曲线相交于点,且,求的值.
23.(本小题满分10分)选修4-5:不等式选讲
已知函数的最小值为3,其中.
(1)求不等式的解集;
(2)若关于的方程有实数根,求实数的取值范围.
陕西师大附中高2024届高三年级
第十次模考数学(理科)详细答案
一、选择题:本题共12小题,每小题5分,共60分.
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 D D B B D C A C B C A B
二、填空题:本大题共4小题,每小题5分,共20分.
题号 13 14 15 16
答案 ①②④
部分选填试题详细解答:
8.【详解】由三视图知:几何体为三棱锥,且三棱锥的一条侧棱与底面垂直,高为2,底面为等腰直角三角形,如图:平面,故平面,所以平面,在等腰直角三角形中,取O为的中点,连,则,所以为三棱锥外接球的球心,设半径为,
由题可得,所以,所以外接球的表面积.
9.【详解】由,得,则圆心,半径,因为过点所作的圆的两条切线相互垂直,所以及两切点构成边长为2的正方形,且对角线,又在直线上,则圆心到直线的距离,解得或,即,根据选项,满足条件的为B.
10.【详解】由题意得小明同学第一题得6分:
第二题选了2个选项,可能得分情况有3种,分别是得0分、4分和6分;
第二题选了1个选项,可能得分情况有3种,分别是得0分、2分和3分;
由于相同总分只记录一次,因此小明的总分情况有:6分、8分、9分、10分、12分、13分、14分、15分共8种情况,所以中位数为,
11.【详解】由题意可知,,直线的方程为.
设,由.得.
所以,所以.由,得.
如图所示,作轴于点,则.
因为,故,
,又,
故.又,得四边形为平行四边形.
所以其面积为,解得.故答案为:.
12.【详解】设函数的最小正周期为,因为函数在上单调递增,
所以,得,因此.
由知的图象关于直线对称,
由知的图象关于点对称.
①,得,
解得,故,
所以,因为的图象关于直线对称,
所以,则,
因为,所以,故,
当时,,满足在上单调递增;
②,得,
解得,故,
所以,因为的图象关于直线对称,
所以,则,因为,所以,
故,当时,,
不满足在上单调递增,故.
14.【详解】因为四边形是圆柱的轴截面,则线段是直径,都是母线.又是底面圆周上异于的一点,于是得.而平面,平面,则.因为平面,则平面,因为平面,因此得,①正确:同理,,②正确:点不在底面内,而直线在底面内,即是两条不同直线,若平面,因平面,与过一点有且只有一条直线垂直于已知平面矛盾,③不正确;因为平面,而平面,于是得平面平面,④正确.
15.【详解】如图所示:由题意知:,设,
则由于,当且仅当,即时取等号,
所以,因为,
所以当时,可以获得观看的最佳视野.
16.【详解】因为,
令,
因为有两个极值点,
所以是方程在上的两根,所以,所以,,所以
设,则
所以当时,,所以在上单调递减,
所以,即的最小值为.
由可得,,取,则设平面的一个法向量.设平面BEF的一个法向量为,由可得,,
取,则是平面的一个法向量.
所以,,
所以平面与平面所成锐二面角的余弦值为.
19.【详解】(1)由题意可知,
所以,因此,即是单调递增数列,且,
由“生成数列”的定义可得.
(2)当时,.
,又,
,当时,.
设数列的前项和为.则.
当时,
又符合上式,所以.
20.【详解】(1)依题意,
又,又,
所以,所以椭圆C的方程为.
(2)由题意可知,直线的斜率存在且不为0,故可设直线:,
,联立直线和椭圆,
化简得,
由题意可知,即,
且,
则
又直线的斜率依次成等比数列.即,
则,所以且,
设点到直线的距离为,
又
所以,
令,
显然在上为增函数,在上为减函数,所以,即,
所以故面积的取值范围为.
21.【详解】(1),所以,
由条件得,得到,又,所以.
(2)由(1)知,由得:,,由题知对恒成立,
令,因为,
当时,,又,
所以当时,恒成立,即单调递减,
所以,条件成立,
当时,,所以条件不成立.综上,的取值范围为.
(3),由(2)知在上恒成立,
当且仅当时取等号,所以,即,所以命题得证.
四.选做题:请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.
22.(本小题满分10分)选修4-4:坐标系与参数方程
【详解】(1)由曲线的参数方程为,(为参数),可得其普通方程,
由,得曲线的极坐标方程.
,由,得曲线的直角坐标方程.
(2)将代入,得.
将逆时针旋转,得的极坐标方程为,
代入曲线的极坐标方程,得.由,
得.即,
解得.因为,所以.
23.(本小题满分10分)选修4—5:不等式选讲
【详解】(1)由,
当且仅当时取等号:因为的最小值为3,所以,又,
所以.所以即,即或或解得,故不等式的解集为.
(2)由,
作出函数的图象及直线,
如图所示,其中.
因为方程有实数根,所以的图象与直线有公共点.
因为过定点,所以当直线经过点时,斜率,
即时,直线与的图像有公共点,也就是方程有实数根;
由图像知,直线的斜率小于直线的斜率时,得,
此时直线与的图像也有公共点,也就是方程有实数根.
即实数的取值范围是.
同课章节目录
