2025人教B版高中数学选择性必修第一册同步练习题(含解析)--第一章 空间向量与立体几何拔高练
文档属性
| 名称 | 2025人教B版高中数学选择性必修第一册同步练习题(含解析)--第一章 空间向量与立体几何拔高练 |

|
|
| 格式 | docx | ||
| 文件大小 | 858.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教B版高中数学选择性必修第一册
综合拔高练
五年高考练
考点1 用空间向量解决立体几何中的证明、求值问题
1.(2023北京,16)如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=.
(1)求证:BC⊥平面PAB;
(2)求二面角A-PC-B的大小.
2.(2023天津,17)三棱台ABC-A1B1C1中,已知A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,N为线段AB的中点,M为线段BC的中点.
(1)求证:A1N∥平面C1MA;
(2)求平面C1MA与平面ACC1A1所成角的余弦值;
(3)求点C到平面C1MA的距离.
3.(2023新课标Ⅱ,20)如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.
(1)证明:BC⊥DA;
(2)点F满足,求二面角D-AB-F的正弦值.
4.(2023全国甲理,18)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°,AA1=2,A1到平面BCC1B1的距离为1.
(1)证明:A1C=AC;
(2)已知AA1与BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.
5.(2023全国乙理,19)如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,BP,AP,BC的中点分别为D,E,O,AD=DO,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
考点2 用空间向量解决立体几何中的最值问题
6.(2021全国甲理,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
7.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
考点3 已知空间角解决立体几何问题
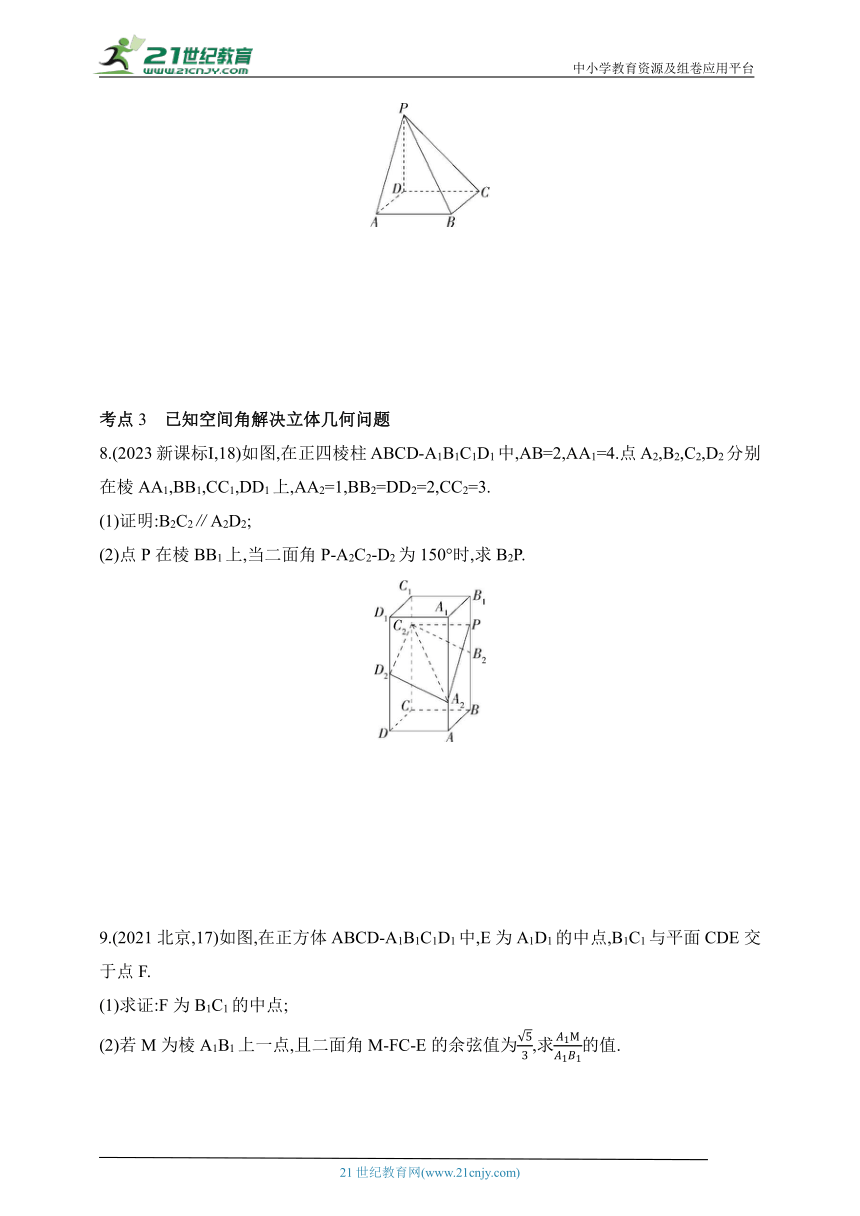
8.(2023新课标Ⅰ,18)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,求B2P.
9.(2021北京,17)如图,在正方体ABCD-A1B1C1D1中,E为A1D1的中点,B1C1与平面CDE交于点F.
(1)求证:F为B1C1的中点;
(2)若M为棱A1B1上一点,且二面角M-FC-E的余弦值为,求的值.
10.(2021新高考Ⅰ,20)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
考点4 用空间向量解决探索性问题
11.(2019北京,16)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且.
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且.判断直线AG是否在平面AEF内,说明理由.
三年模拟练
应用实践
1.(2023北京广渠门中学月考)在四面体A-BCD中,P在平面ABC内,Q在平面BCD内,且满足,若,则线段AQ与DP的位置关系是( )
A.AQ与DP所在直线是异面直线
B.AQ与DP所在直线平行
C.线段AQ与DP必相交
D.线段AQ与DP延长后相交
2.(2024广东广州华南师范大学附属中学期中)如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD、侧面A1ADD1都是正方形,且二面角A1-AD-B的大小为120°,AB=2,若P是C1D与CD1的交点,则AP=( )
A. D.3
3.(2024全国模拟预测)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是棱A1D1,CC1的中点,点G是底面ABCD内任意一点(包括边界),则三棱锥G-B1EF的体积的取值范围是( )
A.
C.
4.(多选题)(2024浙江名校联盟模拟)在正方体ABCD-A1B1C1D1中,AA1=2,点E,F满足,则下列结论正确的有( )
A.直线BE与D1F一定为异面直线
B.直线AE与平面ACB1所成角的正弦值为
C.四面体A-DEF的体积恒为2
D.当λ=μ时,AF+A1F的最小值为
5.(2024江西五校联考)如图,四棱锥P-ABCD中,PA=PB=AB=AD=2,BC=4,AD∥BC,AD⊥AB,AC与BD交于点O,过点O作平行于平面PAB的平面α.
(1)若平面α分别交PC,BC于点E,F,求△OEF的周长;
(2)当PD=2时,求平面α与平面PCD夹角的正弦值.
6.(2024浙江台州教学质量评估)如图1,四边形ABCD为平行四边形,E为CD的中点,AB=4,AD=AE=2,将△ADE沿AE折起,使点D到达点P的位置,如图2.
(1)若平面APE⊥平面ABCE,求证:AP⊥BE;
(2)若点A到直线PC的距离为,求二面角P-AE-B的余弦值.
7.(2024山东潍坊北约联盟期中)已知边长为4的正方形ABCD所在平面与半圆弧所在平面垂直,四边形EFCD是半圆弧的内接梯形,且CD∥EF.
(1)证明:平面ADE⊥平面BCE;
(2)设EF=2,且二面角E-AD-C与二面角D-BC-F的大小都是60°,当点P在棱AD(包含端点)上运动时,求直线PB和平面ACE所成角的正弦值的取值范围.
答案与分层梯度式解析
综合拔高练
五年高考练
1.解析 (1)证明:因为PA⊥平面ABC,BC,AB 平面ABC,所以PA⊥BC,PA⊥AB.
所以PB=.
又因为BC=1,PC=,
所以PB2+BC2=PC2,
所以PB⊥BC.
因为PA∩PB=P,PA,PB 平面PAB,
所以BC⊥平面PAB.
(2)以B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,建立如图所示的空间直角坐标系,则A(0,1,0),B(0,0,0),C(1,0,0),
P(0,1,1),所以
=(1,0,0).
设平面PAC的一个法向量为m=(x1,y1,z1),
则令y1=1,则m=(1,1,0).
设平面PBC的一个法向量为n=(x2,y2,z2),
则令z2=-1,则n=(0,1,-1).
所以cos=.
由图知,二面角A-PC-B为锐二面角,
所以二面角A-PC-B的大小为.
2.解析 (1)证明:连接MN.
因为M,N分别为线段BC,AB的中点,所以MN是△ABC的中位线,所以MN∥AC,MN=AC.
又因为A1C1∥AC,A1C1=AC,所以MN A1C1.
所以四边形MC1A1N是平行四边形,所以MC1∥A1N.
因为MC1 平面C1MA,A1N 平面C1MA,
所以A1N∥平面C1MA.
(2)因为A1A⊥平面ABC,AB,AC 平面ABC,所以A1A⊥AB,A1A⊥AC,又AB⊥AC,所以AB,AC,AA1两两互相垂直.
以A为坐标原点,建立空间直角坐标系,如图所示,
则A(0,0,0),C1(0,1,2),M(1,1,0),C(0,2,0),B(2,0,0),所以=(2,0,0).
设平面C1MA的一个法向量为n=(x,y,z),
则
令x=2,则y=-2,z=1,所以n=(2,-2,1).
易知平面ACC1A1的一个法向量为=(2,0,0).
设平面C1MA与平面ACC1A1所成的角为θ,
则cos θ=|cos所以平面C1MA与平面ACC1A1所成角的余弦值为.
(3)由(2)知,平面C1MA的一个法向量为n=(2,-2,1),=(0,2,0).
所以点C到平面C1MA的距离为.
3.解析 (1)证明:连接AE,DE.
∵DB=DC,E为BC的中点,∴DE⊥BC.
∵DB=DC,∠ADB=∠ADC=60°,DA=DA,
∴△ADB≌△ADC,∴AB=AC,
∴AE⊥BC.
又AE∩DE=E,AE,DE 平面ADE,
∴BC⊥平面ADE,又DA 平面ADE,∴BC⊥DA.
(2)设DA=DB=DC=2,
则AB=AC=2,BC=2,
∴AE2+DE2=AD2,
∴AE⊥DE.
又AE⊥BC,DE∩BC=E,BC,DE 平面BCD,
∴AE⊥平面BCD.
如图,以E为坐标原点,直线ED,EB,EA分别为x轴,y轴,z轴建立空间直角坐标系,
则E(0,0,0),A(0,0,,0),所以).
由,得F(-),所以).
设平面DAB的一个法向量为n=(x,y,z),
则令x=1,得n=(1,1,1),
设平面ABF的一个法向量为m=(x',y',z'),
则
令y'=1,得m=(0,1,1).
设二面角D-AB-F的平面角为θ,θ∈[0,π],
则|cos θ|=,
∴sin θ=,故二面角D-AB-F的正弦值为.
4.解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,∴A1C⊥BC.
∵∠ACB=90°,∴AC⊥BC.
又AC∩A1C=C,AC,A1C 平面AA1C1C,
∴BC⊥平面AA1C1C.
∵BC 平面BCC1B1,
∴平面BCC1B1⊥平面AA1C1C.
过A1作A1H⊥CC1,垂足为H,又平面BCC1B1⊥平面AA1C1C,平面BCC1B1∩平面AA1C1C=CC1,A1H 平面AA1C1C,∴A1H⊥平面BCC1B1,∴A1H=1.
易知∠CA1C1=90°,在Rt△A1CC1中,CC1=2=2A1H,
∴H为CC1的中点,
∴△A1CC1为等腰直角三角形,
∴A1C=A1C1.易知AC A1C1,∴A1C=AC.
(2)以C为坐标原点,CA,CB,CA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.在平面BCC1B1内,过H作HQ∥BC,交BB1于点Q,连接A1Q,如图.
易知CC1⊥A1H,CC1⊥HQ,CC1 BB1,又A1H∩HQ=H,A1H,HQ 平面A1HQ,
∴CC1⊥平面A1HQ,BB1⊥平面A1HQ,又A1Q 平面A1HQ,∴BB1⊥A1Q,
∴A1Q=2,∴在Rt△A1HQ中,HQ=.
易知A1C=AC=,则A(
).
设平面BCC1B1的一个法向量为n=(x,y,z),
则取x=1,得n=(1,0,1).
设直线AB1与平面BCC1B1所成的角为θ,
则sin θ=|cos<,n>|==.
∴AB1与平面BCC1B1所成角的正弦值为.
5.解析 以点B为坐标原点,BA,BC所在直线分别为x轴,y轴,垂直于平面ABC的直线为z轴建立如图所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),O(0,,0).
(1)证明:设,0<λ<1,则F(2-2λ,2λ,0),
∴λ,0),又,0),BF⊥AO,
∴=0,即-2(2-2λ)+4λ=0,解得λ=,故F为AC的中点.
又D,E,O分别为PB,PA,BC的中点,
∴DO∥PC,EF∥PC,∴DO∥EF.
又EF 平面ADO,DO 平面ADO,
∴EF∥平面ADO.
(2)证明:∵D,O分别是PB,BC的中点,且PC=,
∴DO=,又AD=.
由cos∠ABD=,得PA=.
设P(x,y,z),z>0,则由PB=PC=(z>0),解得
故P(-1,).
∵D,E分别是PB,PA的中点,
∴D,
∴,又,0),
∴=0,
∴,即AO⊥BE.
又AO⊥BF,BE∩BF=B,BE,BF 平面BEF,
∴AO⊥平面BEF.
又AO 平面ADO,∴平面ADO⊥平面BEF.
(3)易知平面AOC的一个法向量为m1=(0,0,1).
由(2)知.
设平面AOD的一个法向量为m2=(x1,y1,z1),
则
取x1=1,则y1=,所以m2=(1,).
设二面角D-AO-C的平面角的大小为θ,则|cos θ|=|cos|
=.
∴sin θ=,即二面角D-AO-C的正弦值为.
6.解析 (1)证明:∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,∴A1B1⊥平面B1C1CB.
∵AB∥A1B1,∴AB⊥平面B1C1CB.
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则B(0,0,0),F(0,2,1),E(1,1,0),
∴=(0,2,1).
设B1D=a(0≤a≤2),则D(a,0,2),则=(1-a,1,-2).
∵=0×(1-a)+2×1+1×(-2)=0,∴BF⊥DE.
(2)由(1)知=(a,-2,1).
设平面DFE的一个法向量为n=(x,y,z),
则取x=1,则y=,∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DFE所成的锐二面角的大小为θ,则cos θ=|cos|=,∴sin θ=,
故当a=,即B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小,为.
7.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.因为底面ABCD为正方形,所以AD⊥DC.
所以AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,所以AD∥平面PBC.
由已知得l∥AD.因此l⊥平面PDC.
(2)以D为坐标原点,的方向为x轴正方向建立如图所示的空间直角坐标系Dxyz,则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),所以=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设n=(x,y,z)是平面QCD的一个法向量,
则可取n=(-1,0,a).
所以cos设PB与平面QCD所成的角为θ,
则sin θ=.
因为,当且仅当a=1时,等号成立,
所以PB与平面QCD所成角的正弦值的最大值为.
8.解析 (1)证明:证法一:以C为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,连接A2B2,则A2(2,2,1),B2(0,2,2),C2(0,0,3),D2(2,0,2),
∴.
易知点A2,B2,C2,D2不在同一直线上,∴B2C2∥A2D2.
证法二:分别取DD2,CC1的中点N,M,连接B2M,MN,A2N,A2B2.
在正四棱柱中,BB2=2,BB1=AA1=4,
∴B2为BB1的中点.
易知AA2=1,DN=1,几何体ABB2A2-DCMN为四棱柱,∴四边形A2B2MN为平行四边形,∴MN A2B2.
∵D2N=1,MC2=1,且D2N∥C2M,
∴四边形MND2C2为平行四边形,
∴D2C2 MN,∴A2B2 D2C2,
∴四边形A2B2C2D2为平行四边形,∴B2C2∥A2D2.
(2)同(1)中证法一建系,设BP=t(0≤t≤4),则P(0,2,t).
∵A2(2,2,1),C2(0,0,3),D2(2,0,2),
∴=
(-2,0,1).
设平面PA2C2的一个法向量为u1=(x1,y1,z1),
则
令z1=1,则x1=,∴u1=.
设平面A2C2D2的一个法向量为u2=(x2,y2,z2),
则令z2=2,则x2=1,y2=1,
∴u2=(1,1,2).
设二面角P-A2C2-D2的平面角为θ,则θ=150°.
∴cos θ=cos 150°=,解得t=1或t=3.
当t=1时,BP=1,∴B2P=BB2-BP=1;
当t=3时,BP=3,∴B2P=BP-BB2=1.
综上,B2P=1.
9.解析 (1)证明:在正方体ABCD-A1B1C1D1中,
因为CD∥C1D1,且CD 平面A1B1C1D1,C1D1 平面A1B1C1D1,所以CD∥平面A1B1C1D1.
因为平面CDE∩平面A1B1C1D1=EF,所以CD∥EF.
所以C1D1∥EF.
因为E为A1D1的中点,所以F为B1C1的中点.
(2)不妨设正方体的棱长为2.
如图,建立空间直角坐标系Dxyz,
则D(0,0,0),C(0,2,0),F(1,2,2),
所以=(1,0,2).
设平面CDE的一个法向量为m=(x1,y1,z1),
则
令z1=1,则x1=-2,y1=0,于是m=(-2,0,1).
设,λ∈[0,1),则M(2,2λ,2),
所以=(1,2λ-2,0).
设平面MFC的一个法向量为n=(x2,y2,z2),
则
令x2=2,则z2=-1,y2=,于是n=.
由题意得|cos|=,所以λ=,所以.
10.解析 (1)证明:在△ABD中,∵AB=AD,O为BD的中点,∴AO⊥BD,又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO 平面ABD,
∴AO⊥平面BCD,又CD 平面BCD,∴OA⊥CD.
(2)由OC=OD=OB得BC⊥CD,由(1)知AO⊥平面BCD,以C为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图所示,则C(0,0,0),B(0,,0).
设AO=a,则E.
设平面EBC的一个法向量为n=(x,y,z),
则
令x=a,则z=-1,∴n=(a,0,-1).
易知平面BCD的一个法向量为m=(0,0,1).
由题可知|cos|=,∴a=1,即AO=1,
∴V三棱锥A-BCD=S△BCD·AO=.
11.解析 (1)证明:因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.又因为AD⊥CD,且AD∩PA=A,所以CD⊥平面PAD.
(2)过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),
P(0,0,2),E(0,1,1).
所以=(0,0,2).
所以.
设平面AEF的一个法向量为n=(x,y,z),
则
令z=1,则y=-1,x=-1,所以n=(-1,-1,1).
易知平面PAD的一个法向量为p=(1,0,0).
所以cos=.
由图知,二面角F-AE-P为锐二面角,
所以其余弦值为.
(3)直线AG在平面AEF内.理由如下:
因为点G在PB上,且=(2,-1,-2),
所以.
由(2)知,平面AEF的一个法向量为n=(-1,-1,1).
因为·n=-=0,
所以直线AG在平面AEF内.
三年模拟练
1.C 2.B 3.C 4.ABD
1.C 若x=s=0,则,所以,所以A,P,D,Q四点共面;若x≠0,s≠0,则由,令=m,则,故A,P,D,Q四点共面.又AQ与DP不平行,所以AQ与DP必相交.故选C.
2.B 因为四边形DD1C1C是平行四边形,P是C1D,CD1的交点,所以P是C1D的中点,所以.
因为底面ABCD、侧面A1ADD1都是正方形,所以AA1=AD=AB=2,AB⊥AD,
AA1⊥AD,所以∠A1AB即为二面角A1-AD-B的平面角,即∠A1AB=120°,所以=-2.
所以
=5,所以AP=.故选B.
3.C 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示,
则B1(2,2,2),E(1,0,2),F(0,2,1),
所以=(-1,-2,0).
取EF的中点M,连接B1M,则M,所以.
因为B1E=B1F,M为EF的中点,所以B1M⊥EF,
所以·EF·B1M=.
设平面B1EF的一个法向量为n=(x,y,z),
则
取x=2,得y=-1,z=-4,所以n=(2,-1,-4).
设G(m,n,0)(0≤m≤2,0≤n≤2),则=(2-m,2-n,2),所以点G到平面B1EF的距离为,
所以.
易得-2≤2m-n≤4,所以,
即.故选C.
4.ABD 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),
E(0,0,1),
所以=(-2,0,0).
由(0<λ<1,0<μ<1)得=(-2μ,2,2λ),所以F(2-2μ,2,2λ).
由于0<λ<1,0<μ<1,所以0<2-2μ<2,0<2λ<2,所以点F在平面BCC1B1内(不包括边界),连接BD,B1D1,又D1在平面BB1D1D内,所以D1F和平面BB1D1D相交,
又BE 平面BB1D1D,D1 直线BE,所以直线BE与D1F一定为异面直线,A正确.
易得=(-2,0,1).
设平面ACB1的一个法向量为m=(x,y,z),
则令y=1,得m=(1,1,-1),
所以cos<,m>=,
设直线AE与平面ACB1所成的角为θ,θ∈,
则sin θ=|cos<,m>|=,B正确.
因为点F在平面BCC1B1内(不包括边界),所以点F到平面ADE的距离为2,所以V四面体A-DEF=V四面体F-ADE=,C错误.
当λ=μ时,F(2-2λ,2,2λ),连接BC1,则点F在BC1上(不含端点).
连接A1B,A1C1,将平面A1BC1绕BC1翻折到与平面ABC1D1在同一平面内,如图,
连接AA1,此时AA1与BC1的交点即为满足题意的点F.
由题意可知AB=2,A1B=2,∠ABA1=,
∴A=AB2+A1B2-2AB·A1Bcos∠ABA1=22+(2×
cos ,
∴AF+A1F的最小值为,D正确.
故选ABD.
5.解析 (1)由AD∥BC,可得△AOD∽△COB,∴OB.
由题意得,平面OEF∥平面PAB,又平面OEF∩平面PBC=EF,平面PBC∩平面PAB=PB,∴EF∥PB.
同理可得,OE∥PA,OF∥AB,
∴△PAB∽△EOF,∴.
易得△PAB的周长为6,∴△OEF的周长为4.
(2)∵平面α∥平面PAB,∴平面α与平面PCD的夹角与平面PAB与平面PCD的夹角相等.
∵AD=2,PA=2,PD=2,∴PD2=AD2+PA2,
∴AD⊥PA.
又AD⊥AB,AB∩PA=A,AB,PA 平面PAB,
∴AD⊥平面PAB.
又AD 平面ABCD,
∴平面PAB⊥平面ABCD.
取AB的中点G,连接PG,
则PG⊥AB.
又平面PAB∩平面ABCD=AB,PG 平面PAB,
∴PG⊥平面ABCD.
以点A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,过点A且与PG平行的直线为z轴建立如图所示的空间直角坐标系,
则A(0,0,0),D(0,2,0),P(1,0,).
设平面PCD的一个法向量为n=(x,y,z),
则取x=1,则n=(1,-1,-).
易知=(0,2,0)是平面PAB的一个法向量.
设平面α与平面PCD的夹角为θ,则cos θ=,所以sin θ=,即平面α与平面PCD夹角的正弦值为.
6.解析 (1)证明:因为四边形ABCD为平行四边形,且△ADE为等边三角形,所以∠BCE=120°.
因为E为CD的中点,所以CE=CB,所以△BCE为等腰三角形,所以
∠CEB=30°,所以∠AEB=90°,即BE⊥AE.
因为平面APE⊥平面ABCE,平面APE∩平面ABCE=AE,BE 平面ABCE,所以BE⊥平面APE.
又AP 平面APE,所以AP⊥BE.
(2)取AE的中点O,连接PO.
因为△APE为等边三角形,所以PO⊥AE.
取AB的中点G,连接OG,则OG∥BE.
由(1)得BE⊥AE,所以OG⊥AE.
以点O为坐标原点,OA,OG所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,
则A(1,0,0),C(-2,,0).
设二面角P-AE-B的平面角为θ,即∠POG=θ.
易知OP=,则P(0,cos θ,sin θ),
所以cos θ,-sin θ),
cos θ,-sin θ),
所以点A到直线PC的距离为,解得cos θ=-或cos θ=,所以二面角P-AE-B的余弦值为-.
7.解析 (1)证明:在正方形ABCD中,BC⊥CD.
∵平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,∴BC⊥平面CDE.
∵DE 平面CDE,∴BC⊥DE.
∵E在以CD为直径的半圆上,∴DE⊥EC.
又BC∩CE=C,BC,CE 平面BCE,∴DE⊥平面BCE.
又DE 平面ADE,∴平面ADE⊥平面BCE.
(2)∵AD∥BC,DE⊥BC,∴DE⊥AD,又∵AD⊥DC,∴∠EDC为二面角E-AD-C的平面角,∴∠EDC=60°.同理,∠FCD=60°.∴DE=CF=2.
取CD的中点O,以O为坐标原点建立如图所示的空间直角坐标系,
则A(4,-2,0),B(4,2,0),C(0,2,0),E(0,-1,),
∴).
设P(λ,-2,0),λ∈[0,4],则=(4-λ,4,0).
设平面ACE的一个法向量为n=(x,y,z),
则令x=1,则y=1,z=,
∴n=(1,1,).
设直线PB和平面ACE所成的角为α,
则sin α=|cos<,n>|=.
设t=4-λ,则t∈[0,4],sin α=.
令g(t)=,t∈[0,4],
当t=0时,g(t)=0;
当t≠0时,g(t)=,
易知y=t+在(0,4]上单调递减,
∴t+∈[8,+∞),
∴g(t)∈(0,1].
综上,g(t)=∈[0,1].
∴sin α=,即直线PB和平面ACE所成角的正弦值的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教B版高中数学选择性必修第一册
综合拔高练
五年高考练
考点1 用空间向量解决立体几何中的证明、求值问题
1.(2023北京,16)如图,在三棱锥P-ABC中,PA⊥平面ABC,PA=AB=BC=1,PC=.
(1)求证:BC⊥平面PAB;
(2)求二面角A-PC-B的大小.
2.(2023天津,17)三棱台ABC-A1B1C1中,已知A1A⊥平面ABC,AB⊥AC,AB=AC=AA1=2,A1C1=1,N为线段AB的中点,M为线段BC的中点.
(1)求证:A1N∥平面C1MA;
(2)求平面C1MA与平面ACC1A1所成角的余弦值;
(3)求点C到平面C1MA的距离.
3.(2023新课标Ⅱ,20)如图,三棱锥A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E为BC的中点.
(1)证明:BC⊥DA;
(2)点F满足,求二面角D-AB-F的正弦值.
4.(2023全国甲理,18)如图,在三棱柱ABC-A1B1C1中,A1C⊥平面ABC,∠ACB=90°,AA1=2,A1到平面BCC1B1的距离为1.
(1)证明:A1C=AC;
(2)已知AA1与BB1的距离为2,求AB1与平面BCC1B1所成角的正弦值.
5.(2023全国乙理,19)如图,在三棱锥P-ABC中,AB⊥BC,AB=2,BC=2,BP,AP,BC的中点分别为D,E,O,AD=DO,点F在AC上,BF⊥AO.
(1)证明:EF∥平面ADO;
(2)证明:平面ADO⊥平面BEF;
(3)求二面角D-AO-C的正弦值.
考点2 用空间向量解决立体几何中的最值问题
6.(2021全国甲理,19)已知直三棱柱ABC-A1B1C1中,侧面AA1B1B为正方形,AB=BC=2,E,F分别为AC和CC1的中点,D为棱A1B1上的点,BF⊥A1B1.
(1)证明:BF⊥DE;
(2)当B1D为何值时,面BB1C1C与面DFE所成的二面角的正弦值最小
7.(2020新高考Ⅰ,20)如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.
(1)证明:l⊥平面PDC;
(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.
考点3 已知空间角解决立体几何问题
8.(2023新课标Ⅰ,18)如图,在正四棱柱ABCD-A1B1C1D1中,AB=2,AA1=4.点A2,B2,C2,D2分别在棱AA1,BB1,CC1,DD1上,AA2=1,BB2=DD2=2,CC2=3.
(1)证明:B2C2∥A2D2;
(2)点P在棱BB1上,当二面角P-A2C2-D2为150°时,求B2P.
9.(2021北京,17)如图,在正方体ABCD-A1B1C1D1中,E为A1D1的中点,B1C1与平面CDE交于点F.
(1)求证:F为B1C1的中点;
(2)若M为棱A1B1上一点,且二面角M-FC-E的余弦值为,求的值.
10.(2021新高考Ⅰ,20)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.
(1)证明:OA⊥CD;
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
考点4 用空间向量解决探索性问题
11.(2019北京,16)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且.
(1)求证:CD⊥平面PAD;
(2)求二面角F-AE-P的余弦值;
(3)设点G在PB上,且.判断直线AG是否在平面AEF内,说明理由.
三年模拟练
应用实践
1.(2023北京广渠门中学月考)在四面体A-BCD中,P在平面ABC内,Q在平面BCD内,且满足,若,则线段AQ与DP的位置关系是( )
A.AQ与DP所在直线是异面直线
B.AQ与DP所在直线平行
C.线段AQ与DP必相交
D.线段AQ与DP延长后相交
2.(2024广东广州华南师范大学附属中学期中)如图,在平行六面体ABCD-A1B1C1D1中,底面ABCD、侧面A1ADD1都是正方形,且二面角A1-AD-B的大小为120°,AB=2,若P是C1D与CD1的交点,则AP=( )
A. D.3
3.(2024全国模拟预测)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是棱A1D1,CC1的中点,点G是底面ABCD内任意一点(包括边界),则三棱锥G-B1EF的体积的取值范围是( )
A.
C.
4.(多选题)(2024浙江名校联盟模拟)在正方体ABCD-A1B1C1D1中,AA1=2,点E,F满足,则下列结论正确的有( )
A.直线BE与D1F一定为异面直线
B.直线AE与平面ACB1所成角的正弦值为
C.四面体A-DEF的体积恒为2
D.当λ=μ时,AF+A1F的最小值为
5.(2024江西五校联考)如图,四棱锥P-ABCD中,PA=PB=AB=AD=2,BC=4,AD∥BC,AD⊥AB,AC与BD交于点O,过点O作平行于平面PAB的平面α.
(1)若平面α分别交PC,BC于点E,F,求△OEF的周长;
(2)当PD=2时,求平面α与平面PCD夹角的正弦值.
6.(2024浙江台州教学质量评估)如图1,四边形ABCD为平行四边形,E为CD的中点,AB=4,AD=AE=2,将△ADE沿AE折起,使点D到达点P的位置,如图2.
(1)若平面APE⊥平面ABCE,求证:AP⊥BE;
(2)若点A到直线PC的距离为,求二面角P-AE-B的余弦值.
7.(2024山东潍坊北约联盟期中)已知边长为4的正方形ABCD所在平面与半圆弧所在平面垂直,四边形EFCD是半圆弧的内接梯形,且CD∥EF.
(1)证明:平面ADE⊥平面BCE;
(2)设EF=2,且二面角E-AD-C与二面角D-BC-F的大小都是60°,当点P在棱AD(包含端点)上运动时,求直线PB和平面ACE所成角的正弦值的取值范围.
答案与分层梯度式解析
综合拔高练
五年高考练
1.解析 (1)证明:因为PA⊥平面ABC,BC,AB 平面ABC,所以PA⊥BC,PA⊥AB.
所以PB=.
又因为BC=1,PC=,
所以PB2+BC2=PC2,
所以PB⊥BC.
因为PA∩PB=P,PA,PB 平面PAB,
所以BC⊥平面PAB.
(2)以B为坐标原点,BC所在直线为x轴,BA所在直线为y轴,建立如图所示的空间直角坐标系,则A(0,1,0),B(0,0,0),C(1,0,0),
P(0,1,1),所以
=(1,0,0).
设平面PAC的一个法向量为m=(x1,y1,z1),
则令y1=1,则m=(1,1,0).
设平面PBC的一个法向量为n=(x2,y2,z2),
则令z2=-1,则n=(0,1,-1).
所以cos
由图知,二面角A-PC-B为锐二面角,
所以二面角A-PC-B的大小为.
2.解析 (1)证明:连接MN.
因为M,N分别为线段BC,AB的中点,所以MN是△ABC的中位线,所以MN∥AC,MN=AC.
又因为A1C1∥AC,A1C1=AC,所以MN A1C1.
所以四边形MC1A1N是平行四边形,所以MC1∥A1N.
因为MC1 平面C1MA,A1N 平面C1MA,
所以A1N∥平面C1MA.
(2)因为A1A⊥平面ABC,AB,AC 平面ABC,所以A1A⊥AB,A1A⊥AC,又AB⊥AC,所以AB,AC,AA1两两互相垂直.
以A为坐标原点,建立空间直角坐标系,如图所示,
则A(0,0,0),C1(0,1,2),M(1,1,0),C(0,2,0),B(2,0,0),所以=(2,0,0).
设平面C1MA的一个法向量为n=(x,y,z),
则
令x=2,则y=-2,z=1,所以n=(2,-2,1).
易知平面ACC1A1的一个法向量为=(2,0,0).
设平面C1MA与平面ACC1A1所成的角为θ,
则cos θ=|cos
(3)由(2)知,平面C1MA的一个法向量为n=(2,-2,1),=(0,2,0).
所以点C到平面C1MA的距离为.
3.解析 (1)证明:连接AE,DE.
∵DB=DC,E为BC的中点,∴DE⊥BC.
∵DB=DC,∠ADB=∠ADC=60°,DA=DA,
∴△ADB≌△ADC,∴AB=AC,
∴AE⊥BC.
又AE∩DE=E,AE,DE 平面ADE,
∴BC⊥平面ADE,又DA 平面ADE,∴BC⊥DA.
(2)设DA=DB=DC=2,
则AB=AC=2,BC=2,
∴AE2+DE2=AD2,
∴AE⊥DE.
又AE⊥BC,DE∩BC=E,BC,DE 平面BCD,
∴AE⊥平面BCD.
如图,以E为坐标原点,直线ED,EB,EA分别为x轴,y轴,z轴建立空间直角坐标系,
则E(0,0,0),A(0,0,,0),所以).
由,得F(-),所以).
设平面DAB的一个法向量为n=(x,y,z),
则令x=1,得n=(1,1,1),
设平面ABF的一个法向量为m=(x',y',z'),
则
令y'=1,得m=(0,1,1).
设二面角D-AB-F的平面角为θ,θ∈[0,π],
则|cos θ|=,
∴sin θ=,故二面角D-AB-F的正弦值为.
4.解析 (1)证明:∵A1C⊥平面ABC,BC 平面ABC,∴A1C⊥BC.
∵∠ACB=90°,∴AC⊥BC.
又AC∩A1C=C,AC,A1C 平面AA1C1C,
∴BC⊥平面AA1C1C.
∵BC 平面BCC1B1,
∴平面BCC1B1⊥平面AA1C1C.
过A1作A1H⊥CC1,垂足为H,又平面BCC1B1⊥平面AA1C1C,平面BCC1B1∩平面AA1C1C=CC1,A1H 平面AA1C1C,∴A1H⊥平面BCC1B1,∴A1H=1.
易知∠CA1C1=90°,在Rt△A1CC1中,CC1=2=2A1H,
∴H为CC1的中点,
∴△A1CC1为等腰直角三角形,
∴A1C=A1C1.易知AC A1C1,∴A1C=AC.
(2)以C为坐标原点,CA,CB,CA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.在平面BCC1B1内,过H作HQ∥BC,交BB1于点Q,连接A1Q,如图.
易知CC1⊥A1H,CC1⊥HQ,CC1 BB1,又A1H∩HQ=H,A1H,HQ 平面A1HQ,
∴CC1⊥平面A1HQ,BB1⊥平面A1HQ,又A1Q 平面A1HQ,∴BB1⊥A1Q,
∴A1Q=2,∴在Rt△A1HQ中,HQ=.
易知A1C=AC=,则A(
).
设平面BCC1B1的一个法向量为n=(x,y,z),
则取x=1,得n=(1,0,1).
设直线AB1与平面BCC1B1所成的角为θ,
则sin θ=|cos<,n>|==.
∴AB1与平面BCC1B1所成角的正弦值为.
5.解析 以点B为坐标原点,BA,BC所在直线分别为x轴,y轴,垂直于平面ABC的直线为z轴建立如图所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),O(0,,0).
(1)证明:设,0<λ<1,则F(2-2λ,2λ,0),
∴λ,0),又,0),BF⊥AO,
∴=0,即-2(2-2λ)+4λ=0,解得λ=,故F为AC的中点.
又D,E,O分别为PB,PA,BC的中点,
∴DO∥PC,EF∥PC,∴DO∥EF.
又EF 平面ADO,DO 平面ADO,
∴EF∥平面ADO.
(2)证明:∵D,O分别是PB,BC的中点,且PC=,
∴DO=,又AD=.
由cos∠ABD=,得PA=.
设P(x,y,z),z>0,则由PB=PC=(z>0),解得
故P(-1,).
∵D,E分别是PB,PA的中点,
∴D,
∴,又,0),
∴=0,
∴,即AO⊥BE.
又AO⊥BF,BE∩BF=B,BE,BF 平面BEF,
∴AO⊥平面BEF.
又AO 平面ADO,∴平面ADO⊥平面BEF.
(3)易知平面AOC的一个法向量为m1=(0,0,1).
由(2)知.
设平面AOD的一个法向量为m2=(x1,y1,z1),
则
取x1=1,则y1=,所以m2=(1,).
设二面角D-AO-C的平面角的大小为θ,则|cos θ|=|cos
=.
∴sin θ=,即二面角D-AO-C的正弦值为.
6.解析 (1)证明:∵BF⊥A1B1,B1B⊥A1B1,BF∩B1B=B,∴A1B1⊥平面B1C1CB.
∵AB∥A1B1,∴AB⊥平面B1C1CB.
又∵BC 平面B1C1CB,∴AB⊥BC.
以B为坐标原点,BA,BC,BB1所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则B(0,0,0),F(0,2,1),E(1,1,0),
∴=(0,2,1).
设B1D=a(0≤a≤2),则D(a,0,2),则=(1-a,1,-2).
∵=0×(1-a)+2×1+1×(-2)=0,∴BF⊥DE.
(2)由(1)知=(a,-2,1).
设平面DFE的一个法向量为n=(x,y,z),
则取x=1,则y=,∴n=.
易知m=(1,0,0)是平面BB1C1C的一个法向量.
设平面BB1C1C与平面DFE所成的锐二面角的大小为θ,则cos θ=|cos
故当a=,即B1D=时,面BB1C1C与面DFE所成的二面角的正弦值最小,为.
7.解析 (1)证明:因为PD⊥底面ABCD,所以PD⊥AD.因为底面ABCD为正方形,所以AD⊥DC.
所以AD⊥平面PDC.
因为AD∥BC,AD 平面PBC,所以AD∥平面PBC.
由已知得l∥AD.因此l⊥平面PDC.
(2)以D为坐标原点,的方向为x轴正方向建立如图所示的空间直角坐标系Dxyz,则D(0,0,0),C(0,1,0),B(1,1,0),P(0,0,1),所以=(1,1,-1).
由(1)可设Q(a,0,1),则=(a,0,1).
设n=(x,y,z)是平面QCD的一个法向量,
则可取n=(-1,0,a).
所以cos
则sin θ=.
因为,当且仅当a=1时,等号成立,
所以PB与平面QCD所成角的正弦值的最大值为.
8.解析 (1)证明:证法一:以C为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,连接A2B2,则A2(2,2,1),B2(0,2,2),C2(0,0,3),D2(2,0,2),
∴.
易知点A2,B2,C2,D2不在同一直线上,∴B2C2∥A2D2.
证法二:分别取DD2,CC1的中点N,M,连接B2M,MN,A2N,A2B2.
在正四棱柱中,BB2=2,BB1=AA1=4,
∴B2为BB1的中点.
易知AA2=1,DN=1,几何体ABB2A2-DCMN为四棱柱,∴四边形A2B2MN为平行四边形,∴MN A2B2.
∵D2N=1,MC2=1,且D2N∥C2M,
∴四边形MND2C2为平行四边形,
∴D2C2 MN,∴A2B2 D2C2,
∴四边形A2B2C2D2为平行四边形,∴B2C2∥A2D2.
(2)同(1)中证法一建系,设BP=t(0≤t≤4),则P(0,2,t).
∵A2(2,2,1),C2(0,0,3),D2(2,0,2),
∴=
(-2,0,1).
设平面PA2C2的一个法向量为u1=(x1,y1,z1),
则
令z1=1,则x1=,∴u1=.
设平面A2C2D2的一个法向量为u2=(x2,y2,z2),
则令z2=2,则x2=1,y2=1,
∴u2=(1,1,2).
设二面角P-A2C2-D2的平面角为θ,则θ=150°.
∴cos θ=cos 150°=,解得t=1或t=3.
当t=1时,BP=1,∴B2P=BB2-BP=1;
当t=3时,BP=3,∴B2P=BP-BB2=1.
综上,B2P=1.
9.解析 (1)证明:在正方体ABCD-A1B1C1D1中,
因为CD∥C1D1,且CD 平面A1B1C1D1,C1D1 平面A1B1C1D1,所以CD∥平面A1B1C1D1.
因为平面CDE∩平面A1B1C1D1=EF,所以CD∥EF.
所以C1D1∥EF.
因为E为A1D1的中点,所以F为B1C1的中点.
(2)不妨设正方体的棱长为2.
如图,建立空间直角坐标系Dxyz,
则D(0,0,0),C(0,2,0),F(1,2,2),
所以=(1,0,2).
设平面CDE的一个法向量为m=(x1,y1,z1),
则
令z1=1,则x1=-2,y1=0,于是m=(-2,0,1).
设,λ∈[0,1),则M(2,2λ,2),
所以=(1,2λ-2,0).
设平面MFC的一个法向量为n=(x2,y2,z2),
则
令x2=2,则z2=-1,y2=,于是n=.
由题意得|cos
10.解析 (1)证明:在△ABD中,∵AB=AD,O为BD的中点,∴AO⊥BD,又∵平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO 平面ABD,
∴AO⊥平面BCD,又CD 平面BCD,∴OA⊥CD.
(2)由OC=OD=OB得BC⊥CD,由(1)知AO⊥平面BCD,以C为坐标原点,的方向分别为x轴,y轴,z轴的正方向建立空间直角坐标系,如图所示,则C(0,0,0),B(0,,0).
设AO=a,则E.
设平面EBC的一个法向量为n=(x,y,z),
则
令x=a,则z=-1,∴n=(a,0,-1).
易知平面BCD的一个法向量为m=(0,0,1).
由题可知|cos
∴V三棱锥A-BCD=S△BCD·AO=.
11.解析 (1)证明:因为PA⊥平面ABCD,CD 平面ABCD,所以PA⊥CD.又因为AD⊥CD,且AD∩PA=A,所以CD⊥平面PAD.
(2)过A作AD的垂线交BC于点M.
因为PA⊥平面ABCD,所以PA⊥AM,PA⊥AD.
如图,建立空间直角坐标系Axyz,则A(0,0,0),B(2,-1,0),C(2,2,0),
P(0,0,2),E(0,1,1).
所以=(0,0,2).
所以.
设平面AEF的一个法向量为n=(x,y,z),
则
令z=1,则y=-1,x=-1,所以n=(-1,-1,1).
易知平面PAD的一个法向量为p=(1,0,0).
所以cos
由图知,二面角F-AE-P为锐二面角,
所以其余弦值为.
(3)直线AG在平面AEF内.理由如下:
因为点G在PB上,且=(2,-1,-2),
所以.
由(2)知,平面AEF的一个法向量为n=(-1,-1,1).
因为·n=-=0,
所以直线AG在平面AEF内.
三年模拟练
1.C 2.B 3.C 4.ABD
1.C 若x=s=0,则,所以,所以A,P,D,Q四点共面;若x≠0,s≠0,则由,令=m,则,故A,P,D,Q四点共面.又AQ与DP不平行,所以AQ与DP必相交.故选C.
2.B 因为四边形DD1C1C是平行四边形,P是C1D,CD1的交点,所以P是C1D的中点,所以.
因为底面ABCD、侧面A1ADD1都是正方形,所以AA1=AD=AB=2,AB⊥AD,
AA1⊥AD,所以∠A1AB即为二面角A1-AD-B的平面角,即∠A1AB=120°,所以=-2.
所以
=5,所以AP=.故选B.
3.C 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图所示,
则B1(2,2,2),E(1,0,2),F(0,2,1),
所以=(-1,-2,0).
取EF的中点M,连接B1M,则M,所以.
因为B1E=B1F,M为EF的中点,所以B1M⊥EF,
所以·EF·B1M=.
设平面B1EF的一个法向量为n=(x,y,z),
则
取x=2,得y=-1,z=-4,所以n=(2,-1,-4).
设G(m,n,0)(0≤m≤2,0≤n≤2),则=(2-m,2-n,2),所以点G到平面B1EF的距离为,
所以.
易得-2≤2m-n≤4,所以,
即.故选C.
4.ABD 以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),D(0,0,0),A1(2,0,2),B1(2,2,2),
E(0,0,1),
所以=(-2,0,0).
由(0<λ<1,0<μ<1)得=(-2μ,2,2λ),所以F(2-2μ,2,2λ).
由于0<λ<1,0<μ<1,所以0<2-2μ<2,0<2λ<2,所以点F在平面BCC1B1内(不包括边界),连接BD,B1D1,又D1在平面BB1D1D内,所以D1F和平面BB1D1D相交,
又BE 平面BB1D1D,D1 直线BE,所以直线BE与D1F一定为异面直线,A正确.
易得=(-2,0,1).
设平面ACB1的一个法向量为m=(x,y,z),
则令y=1,得m=(1,1,-1),
所以cos<,m>=,
设直线AE与平面ACB1所成的角为θ,θ∈,
则sin θ=|cos<,m>|=,B正确.
因为点F在平面BCC1B1内(不包括边界),所以点F到平面ADE的距离为2,所以V四面体A-DEF=V四面体F-ADE=,C错误.
当λ=μ时,F(2-2λ,2,2λ),连接BC1,则点F在BC1上(不含端点).
连接A1B,A1C1,将平面A1BC1绕BC1翻折到与平面ABC1D1在同一平面内,如图,
连接AA1,此时AA1与BC1的交点即为满足题意的点F.
由题意可知AB=2,A1B=2,∠ABA1=,
∴A=AB2+A1B2-2AB·A1Bcos∠ABA1=22+(2×
cos ,
∴AF+A1F的最小值为,D正确.
故选ABD.
5.解析 (1)由AD∥BC,可得△AOD∽△COB,∴OB.
由题意得,平面OEF∥平面PAB,又平面OEF∩平面PBC=EF,平面PBC∩平面PAB=PB,∴EF∥PB.
同理可得,OE∥PA,OF∥AB,
∴△PAB∽△EOF,∴.
易得△PAB的周长为6,∴△OEF的周长为4.
(2)∵平面α∥平面PAB,∴平面α与平面PCD的夹角与平面PAB与平面PCD的夹角相等.
∵AD=2,PA=2,PD=2,∴PD2=AD2+PA2,
∴AD⊥PA.
又AD⊥AB,AB∩PA=A,AB,PA 平面PAB,
∴AD⊥平面PAB.
又AD 平面ABCD,
∴平面PAB⊥平面ABCD.
取AB的中点G,连接PG,
则PG⊥AB.
又平面PAB∩平面ABCD=AB,PG 平面PAB,
∴PG⊥平面ABCD.
以点A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,过点A且与PG平行的直线为z轴建立如图所示的空间直角坐标系,
则A(0,0,0),D(0,2,0),P(1,0,).
设平面PCD的一个法向量为n=(x,y,z),
则取x=1,则n=(1,-1,-).
易知=(0,2,0)是平面PAB的一个法向量.
设平面α与平面PCD的夹角为θ,则cos θ=,所以sin θ=,即平面α与平面PCD夹角的正弦值为.
6.解析 (1)证明:因为四边形ABCD为平行四边形,且△ADE为等边三角形,所以∠BCE=120°.
因为E为CD的中点,所以CE=CB,所以△BCE为等腰三角形,所以
∠CEB=30°,所以∠AEB=90°,即BE⊥AE.
因为平面APE⊥平面ABCE,平面APE∩平面ABCE=AE,BE 平面ABCE,所以BE⊥平面APE.
又AP 平面APE,所以AP⊥BE.
(2)取AE的中点O,连接PO.
因为△APE为等边三角形,所以PO⊥AE.
取AB的中点G,连接OG,则OG∥BE.
由(1)得BE⊥AE,所以OG⊥AE.
以点O为坐标原点,OA,OG所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,
则A(1,0,0),C(-2,,0).
设二面角P-AE-B的平面角为θ,即∠POG=θ.
易知OP=,则P(0,cos θ,sin θ),
所以cos θ,-sin θ),
cos θ,-sin θ),
所以点A到直线PC的距离为,解得cos θ=-或cos θ=,所以二面角P-AE-B的余弦值为-.
7.解析 (1)证明:在正方形ABCD中,BC⊥CD.
∵平面ABCD⊥平面CDE,平面ABCD∩平面CDE=CD,∴BC⊥平面CDE.
∵DE 平面CDE,∴BC⊥DE.
∵E在以CD为直径的半圆上,∴DE⊥EC.
又BC∩CE=C,BC,CE 平面BCE,∴DE⊥平面BCE.
又DE 平面ADE,∴平面ADE⊥平面BCE.
(2)∵AD∥BC,DE⊥BC,∴DE⊥AD,又∵AD⊥DC,∴∠EDC为二面角E-AD-C的平面角,∴∠EDC=60°.同理,∠FCD=60°.∴DE=CF=2.
取CD的中点O,以O为坐标原点建立如图所示的空间直角坐标系,
则A(4,-2,0),B(4,2,0),C(0,2,0),E(0,-1,),
∴).
设P(λ,-2,0),λ∈[0,4],则=(4-λ,4,0).
设平面ACE的一个法向量为n=(x,y,z),
则令x=1,则y=1,z=,
∴n=(1,1,).
设直线PB和平面ACE所成的角为α,
则sin α=|cos<,n>|=.
设t=4-λ,则t∈[0,4],sin α=.
令g(t)=,t∈[0,4],
当t=0时,g(t)=0;
当t≠0时,g(t)=,
易知y=t+在(0,4]上单调递减,
∴t+∈[8,+∞),
∴g(t)∈(0,1].
综上,g(t)=∈[0,1].
∴sin α=,即直线PB和平面ACE所成角的正弦值的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
