数学:11.3探索三角形全等的条件同步练习(b卷)(苏科版七年级下)
文档属性
| 名称 | 数学:11.3探索三角形全等的条件同步练习(b卷)(苏科版七年级下) |  | |
| 格式 | rar | ||
| 文件大小 | 45.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-12 15:48:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
11.3探索三角形全等的条件(B卷)
(综合应用创新训练题,共90分,时间:60分钟)
一、实践应用题:(每小题5分,共20分)
1、如图所示,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小,形状完全相同的玻璃,那么他可以带哪块去
2、选做其中一题
A: 一次战役中,我军阵地与敌军碉堡隔河相望(如图所示),需要知道碉堡与我军阵地的距离,在不能过河测量又没任何测量工作的情况下,一个战士想出来这样一个办法;他面向碉堡的位置站好,然后调整帽子, 使视线通过帽檐正好落在碉堡的底部,然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上, 接着他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离,你能解释其中的道理吗
B:如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC 与右边滑梯水平方向的长度为DF相等,求∠ABC+∠DFE的度数.
3、选做其中一题
A:如图所示,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC再定出BF的垂线DE,使A、C、E在同一条直线上,这时测得的DE 的长就是AB的长,写出已知和求证,并且进行证明.
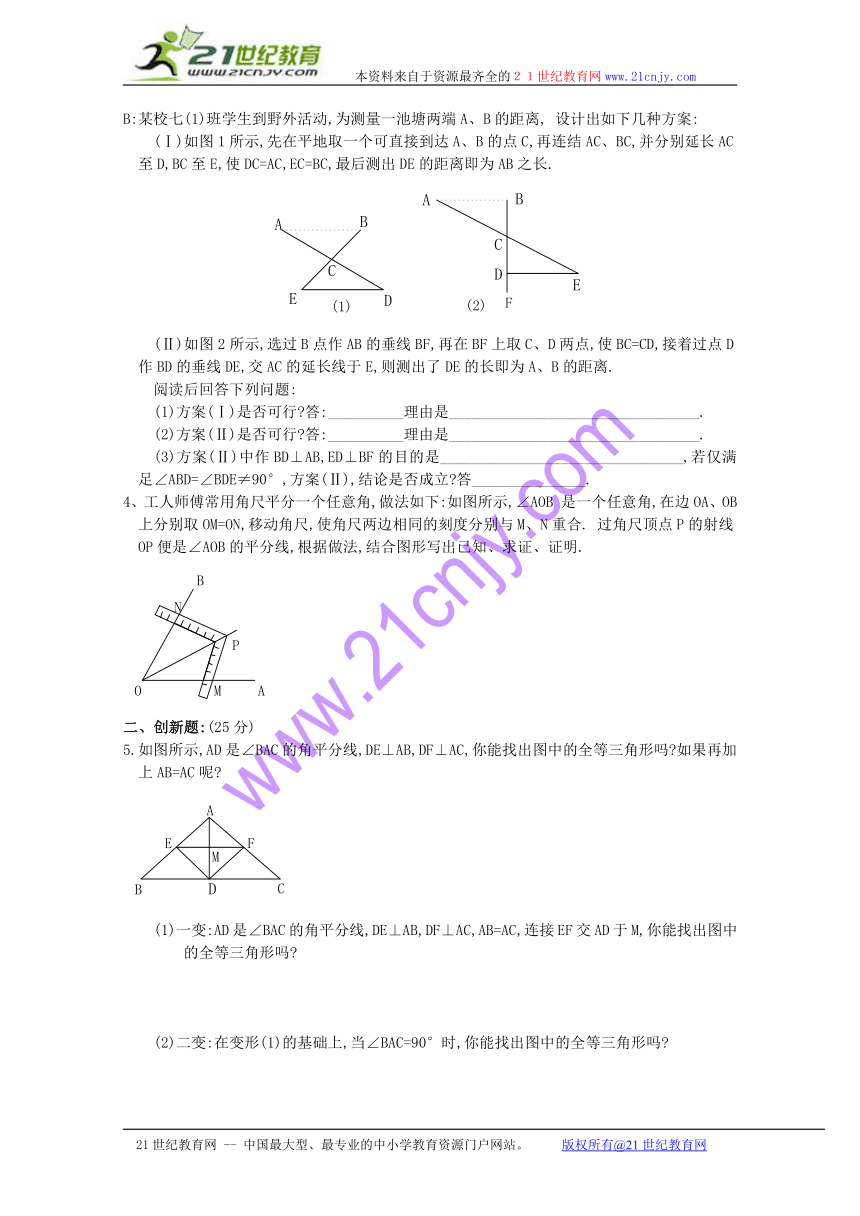
B:某校七(1)班学生到野外活动,为测量一池塘两端A、B的距离, 设计出如下几种方案:
(Ⅰ)如图1所示,先在平地取一个可直接到达A、B的点C,再连结AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长.
(Ⅱ)如图2所示,选过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出了DE的长即为A、B的距离.
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行 答:__________理由是_________________________________.
(2)方案(Ⅱ)是否可行 答:__________理由是_________________________________.
(3)方案(Ⅱ)中作BD⊥AB,ED⊥BF的目的是________________________________,若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ),结论是否成立 答_______________.
4、工人师傅常用角尺平分一个任意角,做法如下:如图所示,∠AOB 是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合. 过角尺顶点P的射线OP便是∠AOB的平分线,根据做法,结合图形写出已知、求证、证明.
二、创新题:(25分)
5.如图所示,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,你能找出图中的全等三角形吗 如果再加上AB=AC呢
(1)一变:AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,AB=AC,连接EF交AD于M,你能找出图中的全等三角形吗
(2)二变:在变形(1)的基础上,当∠BAC=90°时,你能找出图中的全等三角形吗
6.如图所示,已知点C为线段AB上一点,△ACM、△BCN是等边三角形.
(1)求证:AN=BM;
(2)若把原题中“△ACM和△BCN是两个等边三角形”换成两个正方形(如图所示),AN与BM的关系如何 请说明理由.
中考题:(每题5分,共45分)
7.(2003,北京海淀区)如图1所示,点D在AB上,点E在AC上,CD与BE相交于点O, 且AD=AE,AB=AC,若∠B=20°,则∠C=________.
8.(2003,天津)如图2所示,O为ABCD对角线AC、BD的交点,EF经过点O, 且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有 ( )
A.2对 B.3对 C.5对 D.6对
9.(2003,黑龙江)如图3所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、 CE交于点H,请你添加一个适当的条件________,使△AEH≌△CEB.
10.(2003,哈尔滨)如图所示,已知点A、E、F、C在同一条直线上,AD∥BC,AD= CB,AE=CF,求证:BE=DF.
11.(2003,济南)如图4所示,△ABC中,已知AB=AC,要使AD=AE, 需要添加的一个条件是____________.
12.(2003,青岛)如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.
根据上述条件,请在图中找出一对全等三角形,并证明你的结论.
13.(2003,呼和浩特)如图5所示,在△ABC与△DEF中,如果AB=DE,BC=EF,只要再找出∠________=∠________或_________=_________,就可证明这两个三角形全等.
14.(2003,福州)如图所示,已知点A、B、C、D在同一条直线上,AB=CD,∠D= ∠ECA,EC=FD,求证:AE=BF.
15.(2003,长沙)如图所示,若AC、BD、EF两两互相平分于点O, 请写出图中的一对全等三角形(只需写一对即可)_________.
B卷答案
1、带③去.
解:③中已知两角及其夹边作三角形是成立的,即已知:∠A、∠B及AB,求作的△ABC是惟一的,因此,应带③去.
2、
A:解:∵AD⊥BC,∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,∠ADB= ∠ADC=90°,∠DAB=∠DAC,AD=AD,
∴△ADB≌△ADC,∴BD=CD.
B:解:∵AC⊥AB,ED⊥DF,∴∠CAB=∠FDE=90°.
在Rt△ABC和Rt △DEF中,BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF,∴∠BCA=∠EFD,
∵AC⊥AB,∴∠ABC+ ∠BCA=90°,∴∠ABC+∠DFE=90°.
3、A:已知:AB⊥BF,ED⊥BF,垂足分别为B,D,AE交BF于C,BC=DC.
求证:DE=AB.
证明:∵AB⊥BF,ED⊥BF,∴∠ABC=∠EDC=90°.
又∵∠BCA=∠DCE,BC=DE,
∴△BCA≌△DCE,∴AB=DE.
B: (1)可行,由(SAS)全等识别法,证△ACB≌△DCE.
(2)可行;由(ASA)全等识别法,证△ABC≌△EDC.
(3)得∠ABC=∠EDC;成立.
4、已知:OM=ON,PM=PN.
求证:OP平分∠AOB.
证明:在△OPM和△OPN中,OM=ON,PM=PN,OP=OP,
∴△OPM≌△OPN,
∴∠POM=∠PON,故OP平分∠AOB.
5、△AED≌△AFD;△AED≌△AFD,△BED ≌△CFD,△ABD≌△ACD.
(1)答案:△ABD≌ACD,△ADE≌△ADF,△BDE≌△CDF,△AEM≌△AFM,△DEM ≌△DFM.
(2)答案:△ABD≌△ACD,△ADE≌△ADF≌△BDE≌△CDF,△AEM≌△AFM ≌△DEM≌DFM.
6、(1)证明:∵△ACM、△BCN是等边三角形,
∴∠1=∠2=60°,BC=CN,AC=CM,
∴∠1+∠3=∠2+∠3,即∠ACN=∠BCM,
在△ACN和△MCB中,AC=MC, ∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB,∴AN=MB.
(2)AN=BM.理由如下,
∵四边形ACMF、BCNE为正方形,∴AC=MC,CN= CB,∠2=∠1.
在△ACN和△MCB中,AC=MC,∠2=∠1,CN=CB,
∴△ACN≌△MCB,∴AN=BM.
7、20° 8.D 9.AH=CB(只要符合要求即求)
10、证明:如答图所示,
∵AD∥BC,∴∠A=∠C,
∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.
在△ADF和△CBE中, AD=CB,∠A=∠C,AF=CE,
∴△ADF≌△CBE,∴DF=BE.
11、BD=CE.(只要能满足△ABD与△ACE全等的条件即可).
12、△ABF≌△DEA.
证明:∵矩形ABCD,
∴AB=CD,∴∠B=90°,AD∥BC,
∴∠AFB=∠DAE,
又∵DE=CD,∴AB=DE,
∵DE⊥AF,∴∠DAE=90°,
∴∠B=∠DEA.
在△AFB和△DAE中,∠AFB= ∠DAE,∠B=∠DEA,AB=DE,
∴△AFB≌△DAE.
13、∠B=∠DEF或AC=DF
14、证明:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD.
在△EAC和△FBD中,AC=BD,∠ECA= ∠D,EC=FD,
∴△EAC≌△FBD,∴AE=BF.
15、△DOF≌△BOE.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
11.3探索三角形全等的条件(B卷)
(综合应用创新训练题,共90分,时间:60分钟)
一、实践应用题:(每小题5分,共20分)
1、如图所示,某同学把一块三角形的玻璃打破成了三块,现要到玻璃店去配一块大小,形状完全相同的玻璃,那么他可以带哪块去
2、选做其中一题
A: 一次战役中,我军阵地与敌军碉堡隔河相望(如图所示),需要知道碉堡与我军阵地的距离,在不能过河测量又没任何测量工作的情况下,一个战士想出来这样一个办法;他面向碉堡的位置站好,然后调整帽子, 使视线通过帽檐正好落在碉堡的底部,然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上, 接着他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离,你能解释其中的道理吗
B:如图所示,有两个长度相同的滑梯(即BC=EF),左边滑梯的高度AC 与右边滑梯水平方向的长度为DF相等,求∠ABC+∠DFE的度数.
3、选做其中一题
A:如图所示,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC再定出BF的垂线DE,使A、C、E在同一条直线上,这时测得的DE 的长就是AB的长,写出已知和求证,并且进行证明.
B:某校七(1)班学生到野外活动,为测量一池塘两端A、B的距离, 设计出如下几种方案:
(Ⅰ)如图1所示,先在平地取一个可直接到达A、B的点C,再连结AC、BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB之长.
(Ⅱ)如图2所示,选过B点作AB的垂线BF,再在BF上取C、D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于E,则测出了DE的长即为A、B的距离.
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行 答:__________理由是_________________________________.
(2)方案(Ⅱ)是否可行 答:__________理由是_________________________________.
(3)方案(Ⅱ)中作BD⊥AB,ED⊥BF的目的是________________________________,若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ),结论是否成立 答_______________.
4、工人师傅常用角尺平分一个任意角,做法如下:如图所示,∠AOB 是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合. 过角尺顶点P的射线OP便是∠AOB的平分线,根据做法,结合图形写出已知、求证、证明.
二、创新题:(25分)
5.如图所示,AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,你能找出图中的全等三角形吗 如果再加上AB=AC呢
(1)一变:AD是∠BAC的角平分线,DE⊥AB,DF⊥AC,AB=AC,连接EF交AD于M,你能找出图中的全等三角形吗
(2)二变:在变形(1)的基础上,当∠BAC=90°时,你能找出图中的全等三角形吗
6.如图所示,已知点C为线段AB上一点,△ACM、△BCN是等边三角形.
(1)求证:AN=BM;
(2)若把原题中“△ACM和△BCN是两个等边三角形”换成两个正方形(如图所示),AN与BM的关系如何 请说明理由.
中考题:(每题5分,共45分)
7.(2003,北京海淀区)如图1所示,点D在AB上,点E在AC上,CD与BE相交于点O, 且AD=AE,AB=AC,若∠B=20°,则∠C=________.
8.(2003,天津)如图2所示,O为ABCD对角线AC、BD的交点,EF经过点O, 且与边AD、BC分别交于点E、F,若BF=DE,则图中的全等三角形最多有 ( )
A.2对 B.3对 C.5对 D.6对
9.(2003,黑龙江)如图3所示,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、 CE交于点H,请你添加一个适当的条件________,使△AEH≌△CEB.
10.(2003,哈尔滨)如图所示,已知点A、E、F、C在同一条直线上,AD∥BC,AD= CB,AE=CF,求证:BE=DF.
11.(2003,济南)如图4所示,△ABC中,已知AB=AC,要使AD=AE, 需要添加的一个条件是____________.
12.(2003,青岛)如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC.
根据上述条件,请在图中找出一对全等三角形,并证明你的结论.
13.(2003,呼和浩特)如图5所示,在△ABC与△DEF中,如果AB=DE,BC=EF,只要再找出∠________=∠________或_________=_________,就可证明这两个三角形全等.
14.(2003,福州)如图所示,已知点A、B、C、D在同一条直线上,AB=CD,∠D= ∠ECA,EC=FD,求证:AE=BF.
15.(2003,长沙)如图所示,若AC、BD、EF两两互相平分于点O, 请写出图中的一对全等三角形(只需写一对即可)_________.
B卷答案
1、带③去.
解:③中已知两角及其夹边作三角形是成立的,即已知:∠A、∠B及AB,求作的△ABC是惟一的,因此,应带③去.
2、
A:解:∵AD⊥BC,∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,∠ADB= ∠ADC=90°,∠DAB=∠DAC,AD=AD,
∴△ADB≌△ADC,∴BD=CD.
B:解:∵AC⊥AB,ED⊥DF,∴∠CAB=∠FDE=90°.
在Rt△ABC和Rt △DEF中,BC=EF,AC=DF,
∴Rt△ABC≌Rt△DEF,∴∠BCA=∠EFD,
∵AC⊥AB,∴∠ABC+ ∠BCA=90°,∴∠ABC+∠DFE=90°.
3、A:已知:AB⊥BF,ED⊥BF,垂足分别为B,D,AE交BF于C,BC=DC.
求证:DE=AB.
证明:∵AB⊥BF,ED⊥BF,∴∠ABC=∠EDC=90°.
又∵∠BCA=∠DCE,BC=DE,
∴△BCA≌△DCE,∴AB=DE.
B: (1)可行,由(SAS)全等识别法,证△ACB≌△DCE.
(2)可行;由(ASA)全等识别法,证△ABC≌△EDC.
(3)得∠ABC=∠EDC;成立.
4、已知:OM=ON,PM=PN.
求证:OP平分∠AOB.
证明:在△OPM和△OPN中,OM=ON,PM=PN,OP=OP,
∴△OPM≌△OPN,
∴∠POM=∠PON,故OP平分∠AOB.
5、△AED≌△AFD;△AED≌△AFD,△BED ≌△CFD,△ABD≌△ACD.
(1)答案:△ABD≌ACD,△ADE≌△ADF,△BDE≌△CDF,△AEM≌△AFM,△DEM ≌△DFM.
(2)答案:△ABD≌△ACD,△ADE≌△ADF≌△BDE≌△CDF,△AEM≌△AFM ≌△DEM≌DFM.
6、(1)证明:∵△ACM、△BCN是等边三角形,
∴∠1=∠2=60°,BC=CN,AC=CM,
∴∠1+∠3=∠2+∠3,即∠ACN=∠BCM,
在△ACN和△MCB中,AC=MC, ∠ACN=∠MCB,CN=CB,
∴△ACN≌△MCB,∴AN=MB.
(2)AN=BM.理由如下,
∵四边形ACMF、BCNE为正方形,∴AC=MC,CN= CB,∠2=∠1.
在△ACN和△MCB中,AC=MC,∠2=∠1,CN=CB,
∴△ACN≌△MCB,∴AN=BM.
7、20° 8.D 9.AH=CB(只要符合要求即求)
10、证明:如答图所示,
∵AD∥BC,∴∠A=∠C,
∵AE=CF,∴AE+EF=CF+EF,∴AF=CE.
在△ADF和△CBE中, AD=CB,∠A=∠C,AF=CE,
∴△ADF≌△CBE,∴DF=BE.
11、BD=CE.(只要能满足△ABD与△ACE全等的条件即可).
12、△ABF≌△DEA.
证明:∵矩形ABCD,
∴AB=CD,∴∠B=90°,AD∥BC,
∴∠AFB=∠DAE,
又∵DE=CD,∴AB=DE,
∵DE⊥AF,∴∠DAE=90°,
∴∠B=∠DEA.
在△AFB和△DAE中,∠AFB= ∠DAE,∠B=∠DEA,AB=DE,
∴△AFB≌△DAE.
13、∠B=∠DEF或AC=DF
14、证明:∵AB=CD,∴AB+BC=CD+BC,∴AC=BD.
在△EAC和△FBD中,AC=BD,∠ECA= ∠D,EC=FD,
∴△EAC≌△FBD,∴AE=BF.
15、△DOF≌△BOE.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
