专题10.5 数据的收集、整理与描述(全章直通中考)(培优练)(含解析)
文档属性
| 名称 | 专题10.5 数据的收集、整理与描述(全章直通中考)(培优练)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 17:18:39 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题10.5 数据的收集、整理与描述(全章直通中考)(培优练)
一、单选题(本大题共10小题,每小题3分,共30分)
1.(2020·山东日照·中考真题)下列调查中,适宜采用全面调查的是( )
A.调查全国初中学生视力情况
B.了解某班同学“三级跳远”的成绩情况
C.调查某品牌汽车的抗撞击情况
D.调查2019年央视“主持人大赛”节目的收视率
2.(2019·河北·中考真题)某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的种类
②去图书馆收集学生借阅图书的记录
③绘制扇形图来表示各个种类所占的百分比
④整理借阅图书记录并绘制频数分布表
正确统计步骤的顺序是( )
②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→③→①
3.(2011·江苏泰州·中考真题)为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是
A.某市八年级学生的肺活量 B.从中抽取的500名学生的肺活量
C.从中抽取的500名学生 D.500
4.(2011·江苏南京·中考真题)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生 B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生 D.分别从该校初一、初二、初三年级中各随机抽取10%的学生
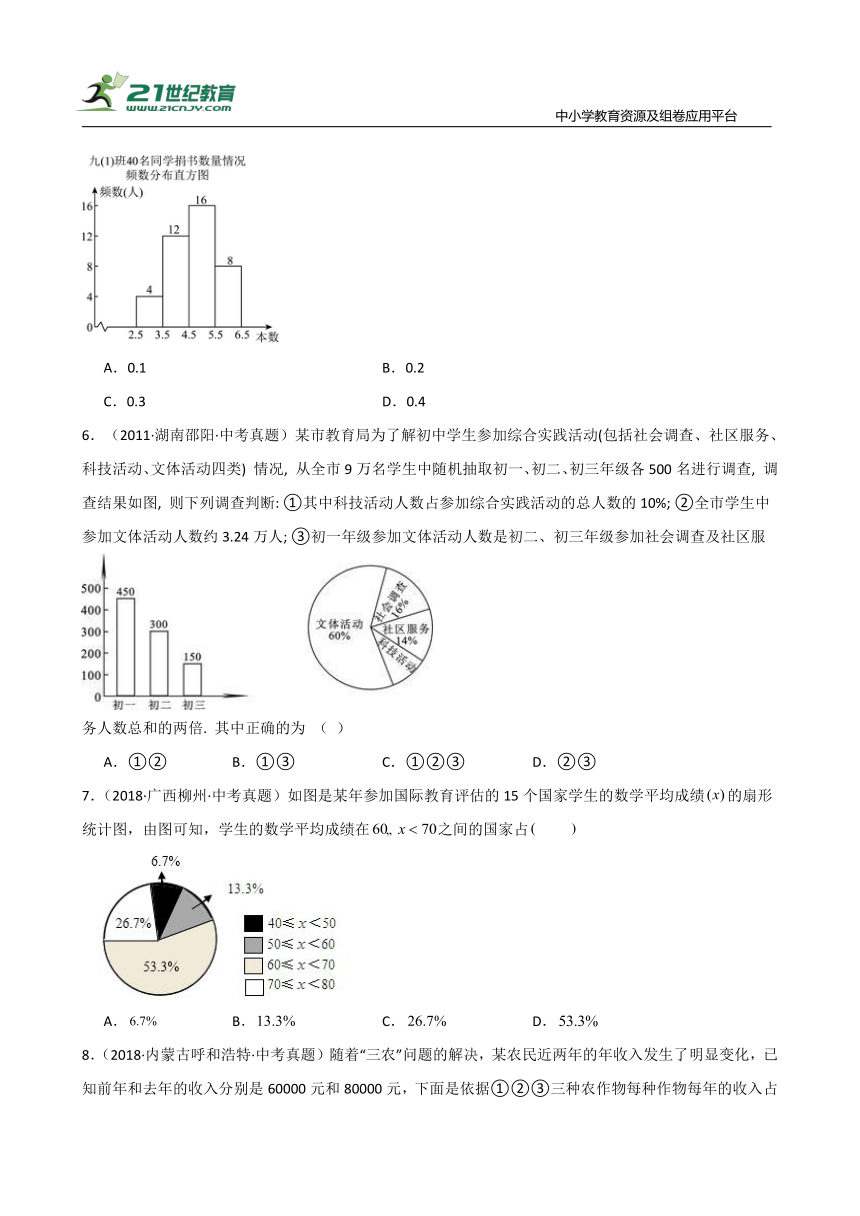
5.(2011·陕西·中考真题)为了支援地震灾区同学,某校开展捐书活动,九(1)班40名同学积极参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是( )
A.0.1 B.0.2
C.0.3 D.0.4
(2011·湖南邵阳·中考真题)某市教育局为了解初中学生参加综合实践活动(包括社会调查、社区服务、科技活动、文体活动四类) 情况, 从全市9万名学生中随机抽取初一、初二、初三年级各500名进行调查, 调查结果如图, 则下列调查判断: ①其中科技活动人数占参加综合实践活动的总人数的10%; ②全市学生中参加文体活动人数约3.24万人; ③初一年级参加文体活动人数是初二、初三年级参加社会调查及社区服
务人数总和的两倍. 其中正确的为 ( )
A.①② B.①③ C.①②③ D.②③
7.(2018·广西柳州·中考真题)如图是某年参加国际教育评估的15个国家学生的数学平均成绩的扇形统计图,由图可知,学生的数学平均成绩在之间的国家占
A. B. C. D.
8.(2018·内蒙古呼和浩特·中考真题)随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
A.①的收入去年和前年相同
B.③的收入所占比例前年的比去年的大
C.去年②的收入为2.8万
D.前年年收入不止①②③三种农作物的收入
9.(2018·云南·中考真题)2017年12月8日,以“[数字工匠]玉汝于成,[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节 玉溪暨第10届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪圆满闭幕.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项错误的是( )
A.抽取的学生人数为50人 B.“非常了解”的人数占抽取的学生人数的12%
C.a=72° D.全校“不了解”的人数估计有428人
10.(2015·内蒙古呼和浩特·中考真题)以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
A.4月份三星手机销售额为65万元
B.4月份三星手机销售额比3月份有所上升
C.4月份三星手机销售额比3月份有所下降
D.3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
二、填空题(本大题共8小题,每小题4分,共32分)
11.(2022·广东深圳·中考真题)某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为 .
12.(2020·湖南永州·中考真题)永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有 人.
13.(2020·湖南·中考真题)4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如表:
阅读时间(x小时) x≤3.5 3.5<x≤5 5<x≤6.5 x>6.5
人数 12 8 6 4
若该校共有1200名学生,试估计全校每周课外阅读时间在5小时以上的学生人数为 .
14.(2020·湖北孝感·中考真题)在线上教学期间,某校落实市教育局要求,督促学生每天做眼保健操.为了解落实情况,学校随机抽取了部分学生进行调查,调查结果分为四类(A类:总时长分钟;B类:5分钟总时长分钟;C类:10分钟总时长分钟;D类:总时长15分钟),将调查所得数据整理并绘制成如下两幅不完整的统计图.
该校共有1200名学生,请根据以上统计分析,估计该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有 人.
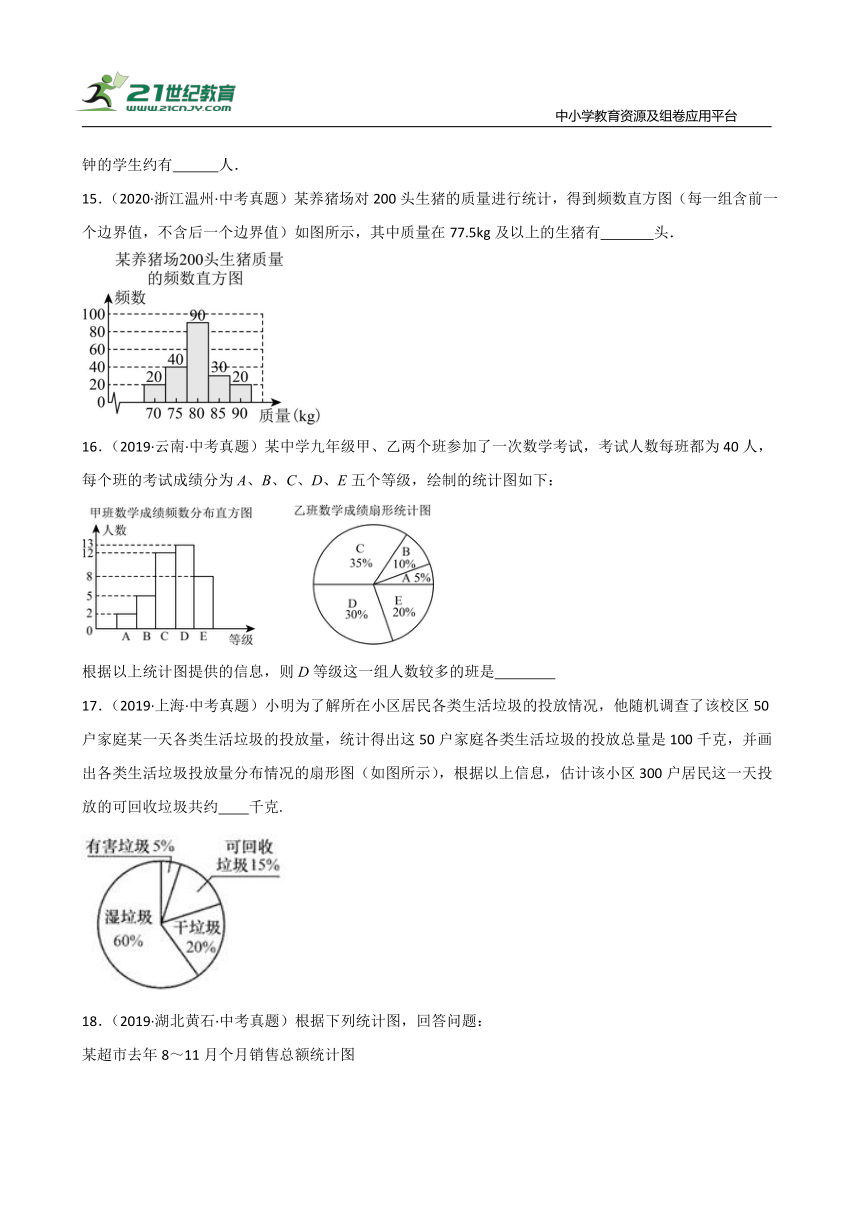
15.(2020·浙江温州·中考真题)某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生猪有 头.
16.(2019·云南·中考真题)某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
根据以上统计图提供的信息,则D等级这一组人数较多的班是
17.(2019·上海·中考真题)小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该校区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区300户居民这一天投放的可回收垃圾共约 千克.
18.(2019·湖北黄石·中考真题)根据下列统计图,回答问题:
某超市去年8~11月个月销售总额统计图
某超市去年8~11月水果销售额占该超市当月销售总额的百分比统计图
该超市10月份的水果类销售额 11月份的水果类销售额(请从“>”“=”“<”中选一个填空)
三、解答题(本大题共6小题,共58分)
19.(8分)(2023·四川甘孜·中考真题)某校为开设足球、篮球、排球选修课程,现对该校学生就“你最喜欢的球类运动”进行抽样调查(要求在“足球”、“篮球”、“排球”中选择一种),将调查数据绘制成如下的两幅统计图.
请根据图中的信息,解答下列问题:
(1)共调查了_________名学生,把条形统计图补充完整;
(2)求扇形统计图中“足球”对应的扇形圆心角的度数;
(3)该校共有名学生,请你估计其中最喜欢排球的学生人数.
20.(8分)(2023·辽宁锦州·中考真题)2023年,教育部等八部门联合印发了《全国青少年学生读书先去实施方案》,某校为落实该方案,成立了四个主题阅读社团:A.民俗文化,B.节日文化,C.古曲诗词,D.红色经典.学校规定:每名学生必须参加且只能一个社团.学校随机对部分学生选择社团的情况进了调查.下面是根据调查结果绘制的两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)本次随机调查的学生有 名,在扇形统计图中“A”部分圆心角的度数为 ;
(2)通过计算补全条形统计图;
(3)若该校共有1800名学生,请根据以上调查结果,估计全校参加“D”社团的人数.
21.(10分)(2023·辽宁鞍山·中考真题)在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时.某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动.评比结果共分为四项:.非凡创意;.魅力色彩;.最美设计;.无限潜力.参赛的每名学生都恰好获得其中一个奖项.活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次共调查了________名学生.
(2)请补全条形统计图.
(3)本次评比活动中,全校有名学生参加,根据调查结果,请你估计在评比中获得“.非凡创意”奖的学生人数.
22.(10分)(2022·内蒙古包头·中考真题)2022年3月28日是第27个全国中小学生安全教育日.某校为调查本校学生对安全知识的了解情况,从全校学生中随机抽取若干名学生进行测试,测试后发现所有测试的学生成绩均不低于50分将全部测试成绩x(单位:分)进行整理后分为五组(,,,,),并绘制成如下的频数直方图(如图).
请根据所给信息,解答下列问题:
(1)在这次调查中,一共抽取了___________名学生;
(2)若测试成绩达到80分及以上为优秀,请你估计全校960名学生对安全知识的了解情况为优秀的学生人数;
(3)为了进一步做好学生安全教育工作,根据调查结果,请你为学校提一条合理化建议.
23.(10分)(2022·四川绵阳·中考真题)目前,全球淡水资源分布不均、总量不足是人类面临的共同问题,某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t) 2≤x<3.5 3.5≤x<5 5≤x<6.5 6.5≤x<8 8≤x<9.5
频数 7 6
对应的扇形区域 A B C D E
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.
24.(12分)(2023·湖南娄底·中考真题)某区教育局为了了解某年级学生对科学知识的掌握情况,在全区范围内随机抽取若干名学生进行科学知识测试,按照测试成绩分优秀、良好、合格与不合格四个等级,并绘制了如下两幅不完整统计图.
(1)参与本次测试的学生人数为______,______.
(2)请补全条形统计图.
(3)若全区该年级共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.B
【分析】根据全面调查和抽样调查的适用条件即可求解.
【详解】解:对于调查方式,适宜于全面调查的常见存在形式有:范围小或准确性要求高的调查,
A.调查全国初中学生视力情况没必要用全面调查,只需抽样调查即可,
B.了解某班同学“三级跳远”的成绩情况,因调查范围小且需要具体到某个人,适宜全面调查,
C.调查某品牌汽车的抗撞击情况,此调查兼破坏性,显然不能适宜全面调查,
D.调查2019年央视“主持人大赛”节目的收视率,因调查受众广范围大,故不适宜全面调查,
故选:B.
【点拨】本题考查全面调查和抽样调查的适用条件,解题关键是要知道这个适用条件.
2.D
【分析】根据频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】由题意可得:正确统计步骤的顺序是:②去图书馆收集学生借阅图书的记录→④整理借阅图书记录并绘制频数分布表→③绘制扇形图来表示各个种类所占的百分比→①从扇形图中分析出最受学生欢迎的种类.
故选D.
【点拨】本题考查了扇形统计图、频数分布表,解答本题的关键是明确制作频数分布表和扇形统计图的制作步骤.
3.B
【详解】∵了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,
这项调查中的样本是500名学生的肺活量,
故选B
4.D
【详解】因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,故只有D符合实际并具有普遍性,故选D.
5.B
【详解】∵在5.5~6.5组别的频数是8,总数是40,
∴=0.2.
故选B.
6.B
【详解】本题考查了条形统计图,从图上知道每组的数据,扇形统计图表示部分占整体的百分比,以及用样本估计总体的知识点.
解:①参加科技活动所占的百分比为:1﹣60%﹣16%﹣14%=10%,故①正确;
②全市参加文体活动的人数约为9×60%=5.4万人,故错误;
③初一参加文体活动的人数为450×60%=270人,
初二、初三参加社会调查及社区服务人数(300+150)×(16%+14%)=135人,
故③正确.
故选B.
7.D
【分析】根据扇形统计图直接反映部分占总体的百分比大小,可知学生成绩在60≤x<69之间的占53.3%.
【详解】由图可知,学生的数学平均成绩在60≤x<70之间的国家占53.3%.
故选D.
【点拨】本题考查的知识点是扇形统计图的应用,解题关键是利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.C
【详解】A、前年①的收入为60000×=19500,去年①的收入为80000×=26000,此选项错误;
B、前年③的收入所占比例为×100%=30%,去年③的收入所占比例为×100%=32.5%,此选项错误;
C、去年②的收入为80000×=28000=2.8(万元),此选项正确;
D、前年年收入即为①②③三种农作物的收入,此选项错误,
故选C.
【点拨】本题主要考查扇形统计图,解题的关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数,并且通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
9.D
【详解】【分析】利用统计图中的信息逐项进行判断即可得解.
【详解】抽取的总人数为6+10+16+18=50(人),故A正确,不符合题意;
“非常了解”的人数占抽取的学生人数的=12%,故B正确,不符合题意;
α=360°×=72°,故C正确,不符合题意;
全校“不了解”的人数估计有1300×=468(人),故D错误,符合题意,
故选D.
【点拨】本题考查了条形统计图、扇形统计图等知识,读懂统计图,从中找到必要的信息是解题的关键.
10.B
【详解】解:三星手机的销售额=单月手机的总销售额×三星手机所占的百分比.
根据统计图可得:三星手机三月份的销售额为:60×18%=10.8(万元),
四月份三星手机的销售额为:65×17%=11.05(万元),则根据以上信息可得B是正确的.
故选:B.
【点拨】本题考查统计图.
11.900人
【分析】符合选拔条件的人数=该工厂总共人数×符合条件的人数所占的百分率,列出算式计算即可求解.
【详解】解:(人).
故答案是:900人.
【点拨】本题考查了用样本估计总体,关键是得到符合条件的人数所占的百分率.
12.480
【分析】用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】(人)
故答案为:480.
【点拨】此题考查用样本的比例估计总体的比例,由此求出对应的总体中的人数,正确理解用样本估计总体的方法是解题的关键.
13.400
【分析】用总人数×每周课外阅读时间在5小时以上的学生人数所占的百分比即可得到结论.
【详解】解:1200×=400(人),
答:估计全校每周课外阅读时间在5小时以上的学生人数为400人.
故答案为:400.
【点拨】本题主要考查了用样本所占百分比估算总体的数量的知识.正确的理解题意是解题的关键.
14.336
【分析】先根据A类的条形统计图和扇形统计图信息求出调查抽取的总人数,再求出每天做眼保健操总时长超过5分钟且不超过10分钟的学生的占比,然后乘以1200即可得.
【详解】调查抽取的总人数为(人)
C类学生的占比为
B类学生的占比为
则(人)
即该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有336人
故答案为:336.
【点拨】本题考查了条形统计图和扇形统计图的信息关联等知识点,掌握理解统计调查的相关知识是解题关键.
15.140
【分析】根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】由直方图可得,
质量在77.5kg及以上的生猪有:90+30+20=140(头),
故答案为:140.
【点拨】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
16.甲班
【分析】分别求出甲班与乙班成绩为D等级的人数进行比较即可.
【详解】解:由频数分布直方图知甲班成绩为D等级的人数为13人,
由扇形统计图知乙班成绩为D等级的人数为40×30%=12,
∴D等级较多的人数是甲班,
故答案为甲班.
【点拨】本题考查了频数分布直方图,扇形统计图,读懂统计图,从中找到必要的信息是解题的关键.
17.90
【分析】根据题意先算出50户家庭可回收垃圾为15千克,再用300户家庭除以50户家庭乘以15即可解答
【详解】100×15%=15千克
×15=90千克
故答案为90千克
【点拨】此题考查扇形统计图,解题关键在于看懂图中数据
18.
【分析】10月份的水果类销售额60×20%=12(万元),11月份的水果类销售额70×15%=10.5(万元),所以10月份的水果类销售额>11月份的水果类销售额.
【详解】10月份的水果类销售额60×20%=12(万元),
11月份的水果类销售额70×15%=10.5(万元),
所以10月份的水果类销售额>11月份的水果类销售额,
故答案为>.
【点拨】本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
19.(1),图见解析
(2)
(3)
【分析】(1)喜欢足球的有人,所占的百分比是,据此即可求得总人数,进而补全统计图;
(2)利用乘以对应的百分比即可求解;
(3)利用总人数乘以对应的百分比即可求解.
【详解】(1)解:调查的总人数是:(人),
故答案为:.
补全条形统计图如图所示:
(2)°.
∴“足球”所对应的扇形圆心角度数为.
(3)(人).
∴估计该校学生中,最喜欢排球的人数约为人.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.(1)60,;
(2)见解析
(3)540名
【分析】
(1)由C组的人数及其所占百分比可得总人数,用乘以A人数所占比例即可得其对应圆心角度数;
(2)根据各类型人数之和等于总人数求得B组的人数,补全图形即可得;
(3)总人数乘以D组人数和所占比例即可.
【详解】(1)本次调查的总人数(名),
扇形统计图中,C所对应的扇形的圆心角度数是,
故答案为:60,;
(2)
(人);
补全条形统计图如答案图所示.
(3)
(名).
答:全校1800名学生中,参加“D”活动小组的学生约有540名.
【点拨】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)
(2)见解析
(3)人
【分析】(1)从两个统计图可知,样本中获得“.无限潜力”的有人,占调查人数的,由频率等于频数除以总数可求出调查人数;
(2)求出样本中获得“.魅力色彩”的人数即可补全条形统计图;
(3)求出样本中获得“.非凡创意”奖的学生所占的百分比,估计总体中获得“A.非凡创意”奖的学生所占的百分比,进而求出相应的人数.
【详解】(1)解: (名),
故答案为:;
(2)样本中获得“.魅力色彩”的人数为:(名),
补全条形统计图如下:
(3)解:(人).
答:全校有名学生中获得“.非凡创意”奖的学生大约有人.
【点拨】本题考查条形统计图、扇形统计图以及样本估计总体,从统计图中获取信息,是解题的关键.
22.(1)40
(2)480人
(3)加强安全知识教育,普及安全知识;通过多种形式(课外活动、知识竞赛等),提高安全意识;结合校内、校外具体活动(应急演练、参观体验、紧急救援等),提高避险能力
【分析】(1)根据频数分布直方图进行求解即可;
(2)由总人数乘以测试成绩达到80分及以上为优秀的比例即可求解;
(3)根据题意提出合理化建议即可.
【详解】(1)由频数分布直方图可得,一共抽取:(人)
故答案为:40;
(2)(人),
所以优秀的学生人数约为480人;
(3)加强安全知识教育,普及安全知识;通过多种形式(课外活动、知识竞赛等),提高安全意识;结合校内、校外具体活动(应急演练、参观体验、紧急救援等),提高避险能力.
【点拨】本题考查了频数直方图,用样本估计总体,准确理解题意,熟练掌握知识点是解题的关键.
23.(1)频数分布直方图见解析,E对应的圆心角的度数为:14.4°
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由见解析
【分析】(1)根据题A的频数和百分比得到抽取的总数,进而求得B、C的频数即可补全频数分布直方图,求出E的频数,360°乘以E所占的比例即可求解;
(2)由于50×60%=30,所以为了鼓励节约用水,要使60%的家庭收费不受影响,即要使30户的家庭收费不受影响,而7+23=30,故家庭月均用水量应该定为5吨.
【详解】(1)抽取的总数为:7÷14%=50,B的频数为:50×46%=23,C的频数为:50×24%=12,频数分布直方图如下:
扇形图中扇形E对应的圆心角的度数为:
360°=14.4°;
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由如下:
因为月平均用水量不超过5吨的有7+23=30(户),30÷50=60%.
【点拨】本题考查了读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
24.(1)150人,
(2)补全图形见解析
(3)3500人.
【分析】(1)由良好60人除以其占比可得总人数,由优秀的45人除以总人数可得m的值;
(2)先利用总人数减去优秀,良好,不合格,得到合格的人数,再补全统计图即可;
(3)由5000乘以测试成绩能达到良好及以上等级的学生人数的占比可得答案.
【详解】(1)解:(人),
∴参与本次测试的学生人数为150人,
,
∴;
故答案为:人;30;
(2)∵(人),
补全图形如下:
.
(3)(人);
∴全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数有3500人.
【点拨】本题考查的是从条形图与扇形图中获取信息,利用样本估计总体,能够正确的读图是解本题的关键.
专题10.5 数据的收集、整理与描述(全章直通中考)(培优练)
一、单选题(本大题共10小题,每小题3分,共30分)
1.(2020·山东日照·中考真题)下列调查中,适宜采用全面调查的是( )
A.调查全国初中学生视力情况
B.了解某班同学“三级跳远”的成绩情况
C.调查某品牌汽车的抗撞击情况
D.调查2019年央视“主持人大赛”节目的收视率
2.(2019·河北·中考真题)某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的种类
②去图书馆收集学生借阅图书的记录
③绘制扇形图来表示各个种类所占的百分比
④整理借阅图书记录并绘制频数分布表
正确统计步骤的顺序是( )
②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→③→①
3.(2011·江苏泰州·中考真题)为了了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,这项调查中的样本是
A.某市八年级学生的肺活量 B.从中抽取的500名学生的肺活量
C.从中抽取的500名学生 D.500
4.(2011·江苏南京·中考真题)为了了解某初中学校学生的视力情况,需要抽取部分学生进行调查.下列抽取学生的方法最合适的是( )
A.随机抽取该校一个班级的学生 B.随机抽取该校一个年级的学生
C.随机抽取该校一部分男生 D.分别从该校初一、初二、初三年级中各随机抽取10%的学生
5.(2011·陕西·中考真题)为了支援地震灾区同学,某校开展捐书活动,九(1)班40名同学积极参与.现将捐书数量绘制成频数分布直方图如图所示,则捐书数量在5.5~6.5组别的频率是( )
A.0.1 B.0.2
C.0.3 D.0.4
(2011·湖南邵阳·中考真题)某市教育局为了解初中学生参加综合实践活动(包括社会调查、社区服务、科技活动、文体活动四类) 情况, 从全市9万名学生中随机抽取初一、初二、初三年级各500名进行调查, 调查结果如图, 则下列调查判断: ①其中科技活动人数占参加综合实践活动的总人数的10%; ②全市学生中参加文体活动人数约3.24万人; ③初一年级参加文体活动人数是初二、初三年级参加社会调查及社区服
务人数总和的两倍. 其中正确的为 ( )
A.①② B.①③ C.①②③ D.②③
7.(2018·广西柳州·中考真题)如图是某年参加国际教育评估的15个国家学生的数学平均成绩的扇形统计图,由图可知,学生的数学平均成绩在之间的国家占
A. B. C. D.
8.(2018·内蒙古呼和浩特·中考真题)随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
A.①的收入去年和前年相同
B.③的收入所占比例前年的比去年的大
C.去年②的收入为2.8万
D.前年年收入不止①②③三种农作物的收入
9.(2018·云南·中考真题)2017年12月8日,以“[数字工匠]玉汝于成,[数字工坊]溪达四海”为主题的2017一带一路数学科技文化节 玉溪暨第10届全国三维数字化创新设计大赛(简称“全国3D大赛”)总决赛在玉溪圆满闭幕.某学校为了解学生对这次大赛的了解程度,在全校1300名学生中随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅统计图.下列四个选项错误的是( )
A.抽取的学生人数为50人 B.“非常了解”的人数占抽取的学生人数的12%
C.a=72° D.全校“不了解”的人数估计有428人
10.(2015·内蒙古呼和浩特·中考真题)以下是某手机店1~4月份的两个统计图,分析统计图,对3、4月份三星手机的销售情况四个同学得出的以下四个结论,其中正确的为( )
A.4月份三星手机销售额为65万元
B.4月份三星手机销售额比3月份有所上升
C.4月份三星手机销售额比3月份有所下降
D.3月份与4月份的三星手机销售额无法比较,只能比较该店销售总额
二、填空题(本大题共8小题,每小题4分,共32分)
11.(2022·广东深圳·中考真题)某工厂一共有1200人,为选拔人才,提出了一些选拔的条件,并进行了抽样调查.从中抽出400人,发现有300人是符合条件的,那么则该工厂1200人中符合选拔条件的人数为 .
12.(2020·湖南永州·中考真题)永州市教育部门为了了解全市中小学安全教育情况,对某校进行了“防溺水”安全知识的测试.从七年级随机抽取了50名学生的测试成绩(百分制),整理样本数据,得到下表:
根据抽样调查结果,估计该校七年级600名学生中,80分(含80分)以上的学生有 人.
13.(2020·湖南·中考真题)4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如表:
阅读时间(x小时) x≤3.5 3.5<x≤5 5<x≤6.5 x>6.5
人数 12 8 6 4
若该校共有1200名学生,试估计全校每周课外阅读时间在5小时以上的学生人数为 .
14.(2020·湖北孝感·中考真题)在线上教学期间,某校落实市教育局要求,督促学生每天做眼保健操.为了解落实情况,学校随机抽取了部分学生进行调查,调查结果分为四类(A类:总时长分钟;B类:5分钟总时长分钟;C类:10分钟总时长分钟;D类:总时长15分钟),将调查所得数据整理并绘制成如下两幅不完整的统计图.
该校共有1200名学生,请根据以上统计分析,估计该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有 人.
15.(2020·浙江温州·中考真题)某养猪场对200头生猪的质量进行统计,得到频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中质量在77.5kg及以上的生猪有 头.
16.(2019·云南·中考真题)某中学九年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A、B、C、D、E五个等级,绘制的统计图如下:
根据以上统计图提供的信息,则D等级这一组人数较多的班是
17.(2019·上海·中考真题)小明为了解所在小区居民各类生活垃圾的投放情况,他随机调查了该校区50户家庭某一天各类生活垃圾的投放量,统计得出这50户家庭各类生活垃圾的投放总量是100千克,并画出各类生活垃圾投放量分布情况的扇形图(如图所示),根据以上信息,估计该小区300户居民这一天投放的可回收垃圾共约 千克.
18.(2019·湖北黄石·中考真题)根据下列统计图,回答问题:
某超市去年8~11月个月销售总额统计图
某超市去年8~11月水果销售额占该超市当月销售总额的百分比统计图
该超市10月份的水果类销售额 11月份的水果类销售额(请从“>”“=”“<”中选一个填空)
三、解答题(本大题共6小题,共58分)
19.(8分)(2023·四川甘孜·中考真题)某校为开设足球、篮球、排球选修课程,现对该校学生就“你最喜欢的球类运动”进行抽样调查(要求在“足球”、“篮球”、“排球”中选择一种),将调查数据绘制成如下的两幅统计图.
请根据图中的信息,解答下列问题:
(1)共调查了_________名学生,把条形统计图补充完整;
(2)求扇形统计图中“足球”对应的扇形圆心角的度数;
(3)该校共有名学生,请你估计其中最喜欢排球的学生人数.
20.(8分)(2023·辽宁锦州·中考真题)2023年,教育部等八部门联合印发了《全国青少年学生读书先去实施方案》,某校为落实该方案,成立了四个主题阅读社团:A.民俗文化,B.节日文化,C.古曲诗词,D.红色经典.学校规定:每名学生必须参加且只能一个社团.学校随机对部分学生选择社团的情况进了调查.下面是根据调查结果绘制的两幅不完整的统计图.
请根据图中提供的信息,解答下列问题:
(1)本次随机调查的学生有 名,在扇形统计图中“A”部分圆心角的度数为 ;
(2)通过计算补全条形统计图;
(3)若该校共有1800名学生,请根据以上调查结果,估计全校参加“D”社团的人数.
21.(10分)(2023·辽宁鞍山·中考真题)在第六十个学雷锋纪念日到来之际,习近平总书记指出:实践证明,无论时代如何变迁,雷锋精神永不过时.某校为弘扬雷锋精神,组织全校学生开展了手抄报评比活动.评比结果共分为四项:.非凡创意;.魅力色彩;.最美设计;.无限潜力.参赛的每名学生都恰好获得其中一个奖项.活动结束后,学校数学兴趣小组随机调查了部分学生的获奖情况,将调查结果绘制成如下两幅不完整的统计图.
请根据统计图提供的信息,解答下列问题:
(1)本次共调查了________名学生.
(2)请补全条形统计图.
(3)本次评比活动中,全校有名学生参加,根据调查结果,请你估计在评比中获得“.非凡创意”奖的学生人数.
22.(10分)(2022·内蒙古包头·中考真题)2022年3月28日是第27个全国中小学生安全教育日.某校为调查本校学生对安全知识的了解情况,从全校学生中随机抽取若干名学生进行测试,测试后发现所有测试的学生成绩均不低于50分将全部测试成绩x(单位:分)进行整理后分为五组(,,,,),并绘制成如下的频数直方图(如图).
请根据所给信息,解答下列问题:
(1)在这次调查中,一共抽取了___________名学生;
(2)若测试成绩达到80分及以上为优秀,请你估计全校960名学生对安全知识的了解情况为优秀的学生人数;
(3)为了进一步做好学生安全教育工作,根据调查结果,请你为学校提一条合理化建议.
23.(10分)(2022·四川绵阳·中考真题)目前,全球淡水资源分布不均、总量不足是人类面临的共同问题,某市在实施居民用水定额管理前,通过简单随机抽样对居民生活用水情况进行了调查,获得了若干个家庭去年的月均用水量数据(单位:t),整理出了频数分布表,频数分布直方图和扇形统计图,部分信息如下:
月均用水量(t) 2≤x<3.5 3.5≤x<5 5≤x<6.5 6.5≤x<8 8≤x<9.5
频数 7 6
对应的扇形区域 A B C D E
根据以上信息,解答下列问题:
(1)补全频数分布直方图,并求出扇形图中扇形E对应的圆心角的度数;
(2)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使该市60%的家庭水费支出不受影响,你觉得家庭月均用水量应该定为多少?并说明理由.
24.(12分)(2023·湖南娄底·中考真题)某区教育局为了了解某年级学生对科学知识的掌握情况,在全区范围内随机抽取若干名学生进行科学知识测试,按照测试成绩分优秀、良好、合格与不合格四个等级,并绘制了如下两幅不完整统计图.
(1)参与本次测试的学生人数为______,______.
(2)请补全条形统计图.
(3)若全区该年级共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.B
【分析】根据全面调查和抽样调查的适用条件即可求解.
【详解】解:对于调查方式,适宜于全面调查的常见存在形式有:范围小或准确性要求高的调查,
A.调查全国初中学生视力情况没必要用全面调查,只需抽样调查即可,
B.了解某班同学“三级跳远”的成绩情况,因调查范围小且需要具体到某个人,适宜全面调查,
C.调查某品牌汽车的抗撞击情况,此调查兼破坏性,显然不能适宜全面调查,
D.调查2019年央视“主持人大赛”节目的收视率,因调查受众广范围大,故不适宜全面调查,
故选:B.
【点拨】本题考查全面调查和抽样调查的适用条件,解题关键是要知道这个适用条件.
2.D
【分析】根据频数分布表、扇形统计图制作的步骤,可以解答本题.
【详解】由题意可得:正确统计步骤的顺序是:②去图书馆收集学生借阅图书的记录→④整理借阅图书记录并绘制频数分布表→③绘制扇形图来表示各个种类所占的百分比→①从扇形图中分析出最受学生欢迎的种类.
故选D.
【点拨】本题考查了扇形统计图、频数分布表,解答本题的关键是明确制作频数分布表和扇形统计图的制作步骤.
3.B
【详解】∵了解某市八年级学生的肺活量,从中抽样调查了500名学生的肺活量,
这项调查中的样本是500名学生的肺活量,
故选B
4.D
【详解】因为要了解初中的视力情况范围较大、难度较大,所以应采取抽样调查的方法比较合适,本题考查的是调查方法的选择,正确选择调查方式要根据全面调查的优缺点再结合实际情况去分析,故只有D符合实际并具有普遍性,故选D.
5.B
【详解】∵在5.5~6.5组别的频数是8,总数是40,
∴=0.2.
故选B.
6.B
【详解】本题考查了条形统计图,从图上知道每组的数据,扇形统计图表示部分占整体的百分比,以及用样本估计总体的知识点.
解:①参加科技活动所占的百分比为:1﹣60%﹣16%﹣14%=10%,故①正确;
②全市参加文体活动的人数约为9×60%=5.4万人,故错误;
③初一参加文体活动的人数为450×60%=270人,
初二、初三参加社会调查及社区服务人数(300+150)×(16%+14%)=135人,
故③正确.
故选B.
7.D
【分析】根据扇形统计图直接反映部分占总体的百分比大小,可知学生成绩在60≤x<69之间的占53.3%.
【详解】由图可知,学生的数学平均成绩在60≤x<70之间的国家占53.3%.
故选D.
【点拨】本题考查的知识点是扇形统计图的应用,解题关键是利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
8.C
【详解】A、前年①的收入为60000×=19500,去年①的收入为80000×=26000,此选项错误;
B、前年③的收入所占比例为×100%=30%,去年③的收入所占比例为×100%=32.5%,此选项错误;
C、去年②的收入为80000×=28000=2.8(万元),此选项正确;
D、前年年收入即为①②③三种农作物的收入,此选项错误,
故选C.
【点拨】本题主要考查扇形统计图,解题的关键是掌握扇形统计图是用整个圆表示总数用圆内各个扇形的大小表示各部分数量占总数的百分数,并且通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.
9.D
【详解】【分析】利用统计图中的信息逐项进行判断即可得解.
【详解】抽取的总人数为6+10+16+18=50(人),故A正确,不符合题意;
“非常了解”的人数占抽取的学生人数的=12%,故B正确,不符合题意;
α=360°×=72°,故C正确,不符合题意;
全校“不了解”的人数估计有1300×=468(人),故D错误,符合题意,
故选D.
【点拨】本题考查了条形统计图、扇形统计图等知识,读懂统计图,从中找到必要的信息是解题的关键.
10.B
【详解】解:三星手机的销售额=单月手机的总销售额×三星手机所占的百分比.
根据统计图可得:三星手机三月份的销售额为:60×18%=10.8(万元),
四月份三星手机的销售额为:65×17%=11.05(万元),则根据以上信息可得B是正确的.
故选:B.
【点拨】本题考查统计图.
11.900人
【分析】符合选拔条件的人数=该工厂总共人数×符合条件的人数所占的百分率,列出算式计算即可求解.
【详解】解:(人).
故答案是:900人.
【点拨】本题考查了用样本估计总体,关键是得到符合条件的人数所占的百分率.
12.480
【分析】用七年级的学生总数乘以样本中80分以上的比例即可得到答案.
【详解】(人)
故答案为:480.
【点拨】此题考查用样本的比例估计总体的比例,由此求出对应的总体中的人数,正确理解用样本估计总体的方法是解题的关键.
13.400
【分析】用总人数×每周课外阅读时间在5小时以上的学生人数所占的百分比即可得到结论.
【详解】解:1200×=400(人),
答:估计全校每周课外阅读时间在5小时以上的学生人数为400人.
故答案为:400.
【点拨】本题主要考查了用样本所占百分比估算总体的数量的知识.正确的理解题意是解题的关键.
14.336
【分析】先根据A类的条形统计图和扇形统计图信息求出调查抽取的总人数,再求出每天做眼保健操总时长超过5分钟且不超过10分钟的学生的占比,然后乘以1200即可得.
【详解】调查抽取的总人数为(人)
C类学生的占比为
B类学生的占比为
则(人)
即该校每天做眼保健操总时长超过5分钟且不超过10分钟的学生约有336人
故答案为:336.
【点拨】本题考查了条形统计图和扇形统计图的信息关联等知识点,掌握理解统计调查的相关知识是解题关键.
15.140
【分析】根据题意和直方图中的数据可以求得质量在77.5kg及以上的生猪数,本题得以解决.
【详解】由直方图可得,
质量在77.5kg及以上的生猪有:90+30+20=140(头),
故答案为:140.
【点拨】本题考查频数分布直方图,解答本题的关键是明确题意,利用数形结合的思想解答.
16.甲班
【分析】分别求出甲班与乙班成绩为D等级的人数进行比较即可.
【详解】解:由频数分布直方图知甲班成绩为D等级的人数为13人,
由扇形统计图知乙班成绩为D等级的人数为40×30%=12,
∴D等级较多的人数是甲班,
故答案为甲班.
【点拨】本题考查了频数分布直方图,扇形统计图,读懂统计图,从中找到必要的信息是解题的关键.
17.90
【分析】根据题意先算出50户家庭可回收垃圾为15千克,再用300户家庭除以50户家庭乘以15即可解答
【详解】100×15%=15千克
×15=90千克
故答案为90千克
【点拨】此题考查扇形统计图,解题关键在于看懂图中数据
18.
【分析】10月份的水果类销售额60×20%=12(万元),11月份的水果类销售额70×15%=10.5(万元),所以10月份的水果类销售额>11月份的水果类销售额.
【详解】10月份的水果类销售额60×20%=12(万元),
11月份的水果类销售额70×15%=10.5(万元),
所以10月份的水果类销售额>11月份的水果类销售额,
故答案为>.
【点拨】本题考查的是条形统计图和折线统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.
19.(1),图见解析
(2)
(3)
【分析】(1)喜欢足球的有人,所占的百分比是,据此即可求得总人数,进而补全统计图;
(2)利用乘以对应的百分比即可求解;
(3)利用总人数乘以对应的百分比即可求解.
【详解】(1)解:调查的总人数是:(人),
故答案为:.
补全条形统计图如图所示:
(2)°.
∴“足球”所对应的扇形圆心角度数为.
(3)(人).
∴估计该校学生中,最喜欢排球的人数约为人.
【点拨】本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
20.(1)60,;
(2)见解析
(3)540名
【分析】
(1)由C组的人数及其所占百分比可得总人数,用乘以A人数所占比例即可得其对应圆心角度数;
(2)根据各类型人数之和等于总人数求得B组的人数,补全图形即可得;
(3)总人数乘以D组人数和所占比例即可.
【详解】(1)本次调查的总人数(名),
扇形统计图中,C所对应的扇形的圆心角度数是,
故答案为:60,;
(2)
(人);
补全条形统计图如答案图所示.
(3)
(名).
答:全校1800名学生中,参加“D”活动小组的学生约有540名.
【点拨】本题考查条形统计图、扇形统计图、用样本估计总体,解答本题的关键是明确题意,利用数形结合的思想解答.
21.(1)
(2)见解析
(3)人
【分析】(1)从两个统计图可知,样本中获得“.无限潜力”的有人,占调查人数的,由频率等于频数除以总数可求出调查人数;
(2)求出样本中获得“.魅力色彩”的人数即可补全条形统计图;
(3)求出样本中获得“.非凡创意”奖的学生所占的百分比,估计总体中获得“A.非凡创意”奖的学生所占的百分比,进而求出相应的人数.
【详解】(1)解: (名),
故答案为:;
(2)样本中获得“.魅力色彩”的人数为:(名),
补全条形统计图如下:
(3)解:(人).
答:全校有名学生中获得“.非凡创意”奖的学生大约有人.
【点拨】本题考查条形统计图、扇形统计图以及样本估计总体,从统计图中获取信息,是解题的关键.
22.(1)40
(2)480人
(3)加强安全知识教育,普及安全知识;通过多种形式(课外活动、知识竞赛等),提高安全意识;结合校内、校外具体活动(应急演练、参观体验、紧急救援等),提高避险能力
【分析】(1)根据频数分布直方图进行求解即可;
(2)由总人数乘以测试成绩达到80分及以上为优秀的比例即可求解;
(3)根据题意提出合理化建议即可.
【详解】(1)由频数分布直方图可得,一共抽取:(人)
故答案为:40;
(2)(人),
所以优秀的学生人数约为480人;
(3)加强安全知识教育,普及安全知识;通过多种形式(课外活动、知识竞赛等),提高安全意识;结合校内、校外具体活动(应急演练、参观体验、紧急救援等),提高避险能力.
【点拨】本题考查了频数直方图,用样本估计总体,准确理解题意,熟练掌握知识点是解题的关键.
23.(1)频数分布直方图见解析,E对应的圆心角的度数为:14.4°
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由见解析
【分析】(1)根据题A的频数和百分比得到抽取的总数,进而求得B、C的频数即可补全频数分布直方图,求出E的频数,360°乘以E所占的比例即可求解;
(2)由于50×60%=30,所以为了鼓励节约用水,要使60%的家庭收费不受影响,即要使30户的家庭收费不受影响,而7+23=30,故家庭月均用水量应该定为5吨.
【详解】(1)抽取的总数为:7÷14%=50,B的频数为:50×46%=23,C的频数为:50×24%=12,频数分布直方图如下:
扇形图中扇形E对应的圆心角的度数为:
360°=14.4°;
(2)要使60%的家庭收费不受影响,家庭月均用水量应该定为5吨,理由如下:
因为月平均用水量不超过5吨的有7+23=30(户),30÷50=60%.
【点拨】本题考查了读频数分布直方图和频数分布表的能力及利用统计图表获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
24.(1)150人,
(2)补全图形见解析
(3)3500人.
【分析】(1)由良好60人除以其占比可得总人数,由优秀的45人除以总人数可得m的值;
(2)先利用总人数减去优秀,良好,不合格,得到合格的人数,再补全统计图即可;
(3)由5000乘以测试成绩能达到良好及以上等级的学生人数的占比可得答案.
【详解】(1)解:(人),
∴参与本次测试的学生人数为150人,
,
∴;
故答案为:人;30;
(2)∵(人),
补全图形如下:
.
(3)(人);
∴全区该年纪共有5000名学生,请估计该年级对科学知识掌握情况较好(测试成绩能达到良好及以上等级)的学生人数有3500人.
【点拨】本题考查的是从条形图与扇形图中获取信息,利用样本估计总体,能够正确的读图是解本题的关键.
