【浙教版九上同步练习】九年级上册综合练习数学试题二(含答案)
文档属性
| 名称 | 【浙教版九上同步练习】九年级上册综合练习数学试题二(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版九上同步练习】
九上全册综合题二
一、单选题
1.如图,已知 , ,下列不能判定 的条件是( ).
A. B. C. D.
2.在一个不透明的袋子中装有2个红球、1个黄球和1个黑球,这些球的形状、大小、质地等完全相同,若随机从袋子里摸出1个球,则摸出红球的概率是( )
A. B. C. D.
3.抛物线 的顶点坐标是( )
A. B. C. D.
4.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
5.一次函数 的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
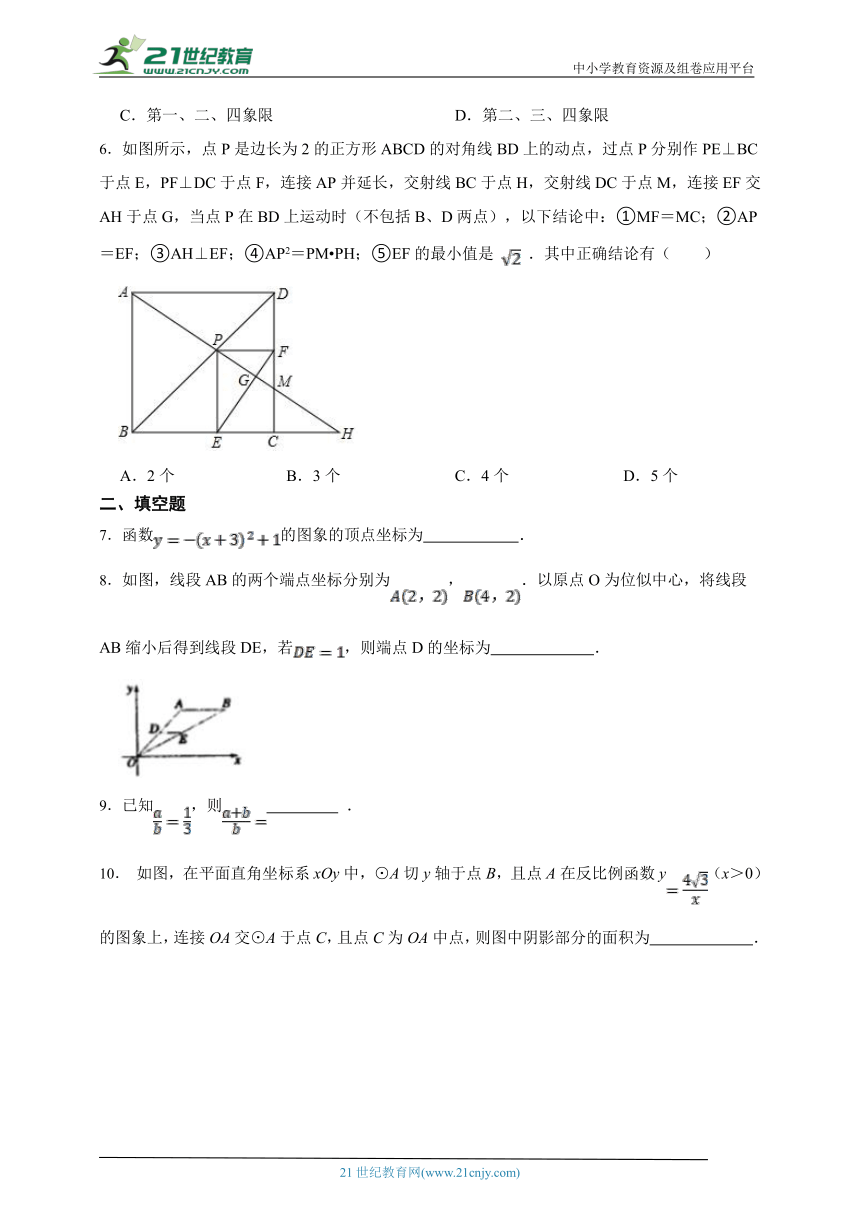
6.如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PM PH;⑤EF的最小值是 .其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
7.函数的图象的顶点坐标为 .
8.如图,线段AB的两个端点坐标分别为,.以原点O为位似中心,将线段AB缩小后得到线段DE,若,则端点D的坐标为 .
9.已知,则 .
10. 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为 .
三、判断题
11.一幅图的比例尺是1:200000厘米。
12.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
13.如图,转盘分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字.三位同学发表了下述见解,正确的在括号内打“√”,错误的打“×”.
(1)甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形.( )
(2)乙:只要指针连续转六次,一定会有一次停在6 号扇形. ( )
(3)丙:在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.( )
14.圆的周长是直径的 π 倍.(判断对错)
四、计算题
15.若a:b=1:2,求(a+b):a的值.
16.
(1)计算:
(2)解方程:4x(x+3)=x2﹣9
17.解方程:
五、解答题
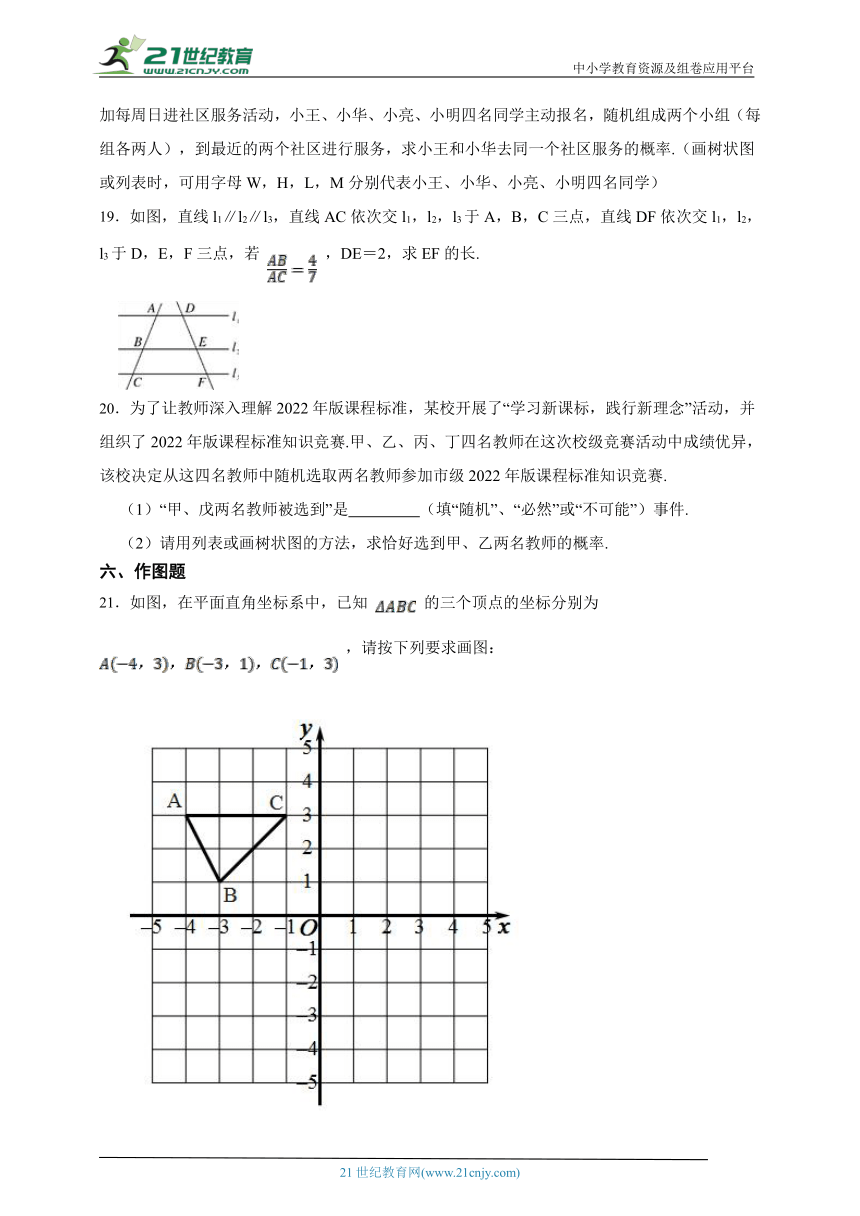
18.今年5月11日至12日,习近平总书记考察山西时指出,“要加强社区建设和管理,加强社区环境整治……,增强太原人民的获得感、幸福感、安全感”.随后,全市上下认真学习和贯彻这一重要指示精神,掀起了创建全国文明城市的高潮,学校学生会和校团委积极响应招募志愿者参加每周日进社区服务活动,小王、小华、小亮、小明四名同学主动报名,随机组成两个小组(每组各两人),到最近的两个社区进行服务,求小王和小华去同一个社区服务的概率.(画树状图或列表时,可用字母W,H,L,M分别代表小王、小华、小亮、小明四名同学)
19.如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于A,B,C三点,直线DF依次交l1,l2,l3于D,E,F三点,若 ,DE=2,求EF的长.
20.为了让教师深入理解2022年版课程标准,某校开展了“学习新课标,践行新理念”活动,并组织了2022年版课程标准知识竞赛.甲、乙、丙、丁四名教师在这次校级竞赛活动中成绩优异,该校决定从这四名教师中随机选取两名教师参加市级2022年版课程标准知识竞赛.
(1)“甲、戊两名教师被选到”是 (填“随机”、“必然”或“不可能”)事件.
(2)请用列表或画树状图的方法,求恰好选到甲、乙两名教师的概率.
六、作图题
21.如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 ,请按下列要求画图:
(1)将 先向右平移4个单位长度、再向下平移5个单位长度,得到 ,画出 ,并写出点 的坐标;
(2)以点 为位似中心将 放大2倍,得到 ,画出 并写出点B的坐标.
七、综合题
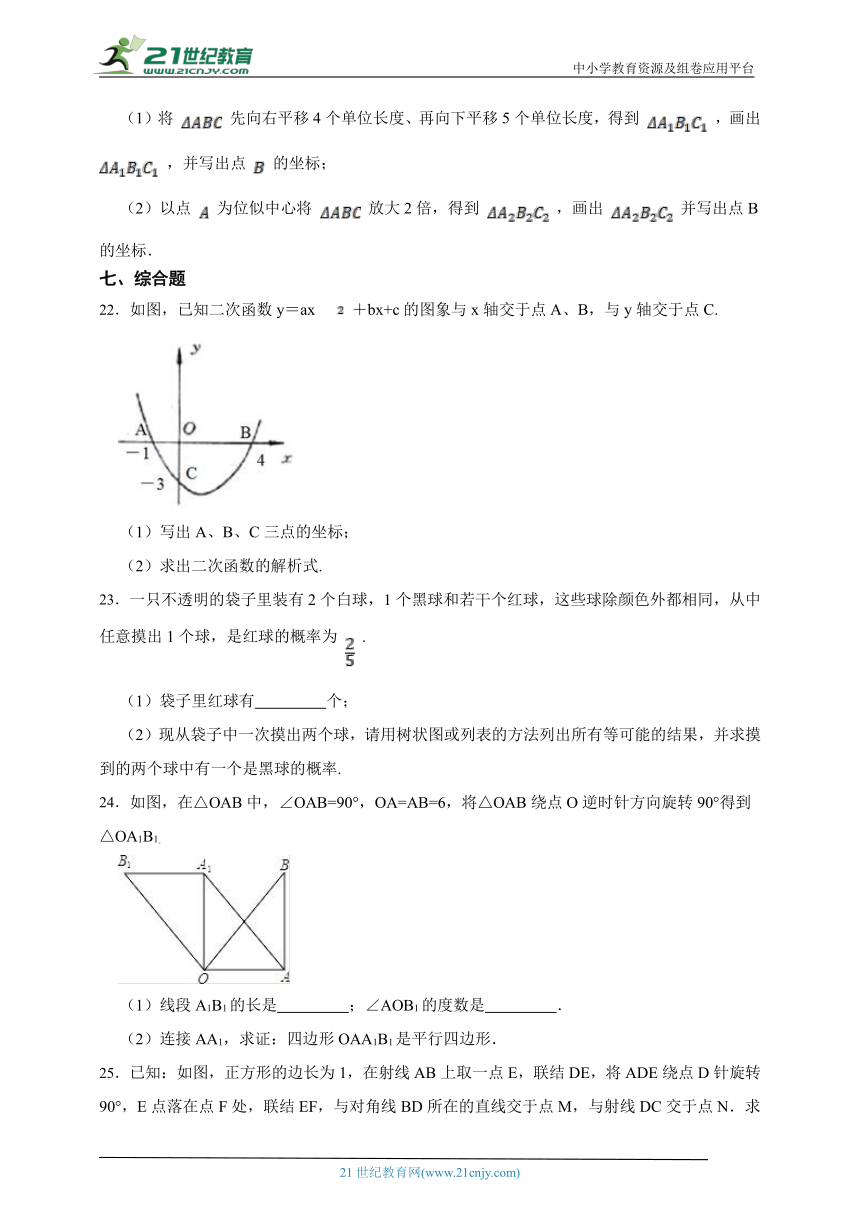
22.如图,已知二次函数y=ax +bx+c的图象与x轴交于点A、B,与y轴交于点C.
(1)写出A、B、C三点的坐标;
(2)求出二次函数的解析式.
23.一只不透明的袋子里装有2个白球,1个黑球和若干个红球,这些球除颜色外都相同,从中任意摸出1个球,是红球的概率为 .
(1)袋子里红球有 个;
(2)现从袋子中一次摸出两个球,请用树状图或列表的方法列出所有等可能的结果,并求摸到的两个球中有一个是黑球的概率.
24.如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°得到△OA1B1.
(1)线段A1B1的长是 ;∠AOB1的度数是 .
(2)连接AA1,求证:四边形OAA1B1是平行四边形.
25.已知:如图,正方形的边长为1,在射线AB上取一点E,联结DE,将ADE绕点D针旋转90°,E点落在点F处,联结EF,与对角线BD所在的直线交于点M,与射线DC交于点N.求证:
(1)当时,求的值;
(2)当点E在线段AB上,如果,,求y关于x的函数解析式,并写出定义域;
(3)联结AM,直线AM与直线BC交于点G,当时,求AE的值.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定
2.【答案】C
【知识点】概率公式
3.【答案】B
【知识点】二次函数y=a(x-h)^2+k的图象
4.【答案】B
【知识点】二次函数图象与系数的关系
5.【答案】B
【知识点】一次函数图象、性质与系数的关系
6.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定;正方形的性质;相似三角形的判定与性质
7.【答案】
【知识点】二次函数y=a(x-h)^2+k的图象
8.【答案】(1,1)
【知识点】位似变换
9.【答案】
【知识点】比例的性质
10.【答案】2
【知识点】扇形面积的计算;反比例函数图象上点的坐标特征;几何图形的面积计算-割补法
11.【答案】错误
【知识点】比例尺
12.【答案】(1)正确
(2)错误
【知识点】垂径定理
13.【答案】(1)错误
(2)错误
(3)错误
【知识点】事件发生的可能性
14.【答案】正确
【知识点】圆的认识
15.【答案】解:∵a:b=1:2,
∴b=2a,
∴(a+b):a=(a+2a):a=3.
【知识点】比例的性质
16.【答案】(1)解:原式=2﹣2× +| ﹣1|+1
=2﹣ + ﹣1+1
=2;
(2)解:方程整理得:4x2+12x=x2﹣9,即x2+4x+3=0,
分解因式得:(x+1)(x+3)=0,
可得x+1=0或x+3=0,
解得:x1=﹣1,x2=﹣3.
【知识点】零指数幂;负整数指数幂;特殊角的三角函数值
17.【答案】解:
或
或
【知识点】因式分解法解一元二次方程
18.【答案】解:画树状图如下图:
共有12种等可能的结果,其中小王和小华去同一个社区服务的结果有4个,
∴小王和小华去同一个社区服务的概率为: .
【知识点】列表法与树状图法;复合事件概率的计算
19.【答案】解:∵l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,
∴ ,
∵ ,DE=2,
∴ ,
解得:DF=3.5,
∴EF=DF-DE=3.5-2=1.5
【知识点】平行线分线段成比例
20.【答案】(1)不可能
(2)
【知识点】随机事件;列表法与树状图法;概率的简单应用
21.【答案】(1)解:根据题意可得:
∴
(2)解:根据题意可得:
∴
【知识点】作图﹣平移;作图﹣位似变换
22.【答案】(1)A、B、C三点的坐标为A(-1,0),B(4,0),C(0,-3
(2)解:把A(-1,0),B(4,0),C(0,-3)代入y=ax2+bx+c可得
,
解得
∴y=
【知识点】待定系数法求二次函数解析式
23.【答案】(1)2
(2)解:画树状图如图:
共有20个等可能的结果,摸到的两个球中有一个是黑球的结果有8个,
∴摸到的两个球中有一个是黑球的概率为 .
【知识点】概率公式;等可能事件的概率
24.【答案】(1)6;135°
(2)解:∵∠A1OA=∠OA1B1=90°,∴A1B1∥OA,
又∵OA=AB=A1B1
∴四边形OAA1B1是平行四边形.
【知识点】平行四边形的判定;旋转的性质
25.【答案】(1)解:过点E作EH⊥BD与H,
∵正方形的边长为1,,
∴EB=1-,
∵BD为正方形对角线,
∴BD平分∠ABC,
∴∠ABD=45°,
∵EH⊥BD,
∴∠BEH=180°-∠EBH-∠EHB=180°-45°-90°=45°,
∴EH=BH,
∴EH=BH=BEsin45=,AB=BDcos45°,
∴,
∴DH=DB-BH=,
;
(2)解:如上图,∵AE=x,
∴BE=1-x,
∵将△ADE绕点D针旋转90°,得到△DCF,
∴CF=AE=x,ED=FD=,
∴BF=BC+CF=1+x,
在Rt△EBF中EF=,
∵∠EDF=90°,ED=FD,
∴△DEF为等腰直角三角形,
∴∠DFE=∠DEF=45°,
∴∠EBM=∠MFD=45°,
∵∠EMB=∠DMF,
∴△BEM∽△FDM,
∴,即,
∵∠DEM=∠FBM=45°,∠EMD=∠BMF,
∴△EMD∽△BMF,
∴,即,
∴,
∴,
∴即,
∴,0≤x≤1
(3)解:当点G在BC上,,
∵四边形ABCD为正方形,
∴AD∥BG,
∴∠DAM=∠BGM,∠ADM=∠GBM,
∴△BGM∽△DAM,
∴,
∵由(2)知△BEM∽△FDM,
∴,
∵DB=,
∴,
∴,
∴,
∵,
∴即,
解,舍去;
当点G在CB延长线上,,过M作ML⊥BC,交直线BC于L,
∵GB∥AD,
∴∴∠DAM=∠BGM,∠ADM=∠GBM,
∴△BGM∽△DAM,
∴,
∴,
∴,
∵∠LBM=∠CBD=45°,ML⊥BC,
∴△MLB为等腰直角三角形,
∵ML∥CD,
∴∠LMB=∠CDB,∠L=∠DCB,
∴△MLB∽△DCB,
∴,CD=1,
∴ML=
∵ML∥BE,
∴∠L=∠FBE,∠LMF=∠BEF,
∴△LMF∽△BEF,
∴,
∵BE=AE-AB=x-1,LF=LB+BC+CF=,BF=BC+CF=1+x,
∴,
整理得:,
解得,舍去,
∴AE的值为或.
【知识点】正方形的性质;相似三角形的判定与性质;旋转的性质;四边形的综合
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版九上同步练习】
九上全册综合题二
一、单选题
1.如图,已知 , ,下列不能判定 的条件是( ).
A. B. C. D.
2.在一个不透明的袋子中装有2个红球、1个黄球和1个黑球,这些球的形状、大小、质地等完全相同,若随机从袋子里摸出1个球,则摸出红球的概率是( )
A. B. C. D.
3.抛物线 的顶点坐标是( )
A. B. C. D.
4.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;②>0;③ac﹣b+1=0;④OA OB=﹣.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
5.一次函数 的图象经过( )
A.第一、二、三象限 B.第一、三、四象限
C.第一、二、四象限 D.第二、三、四象限
6.如图所示,点P是边长为2的正方形ABCD的对角线BD上的动点,过点P分别作PE⊥BC于点E,PF⊥DC于点F,连接AP并延长,交射线BC于点H,交射线DC于点M,连接EF交AH于点G,当点P在BD上运动时(不包括B、D两点),以下结论中:①MF=MC;②AP=EF;③AH⊥EF;④AP2=PM PH;⑤EF的最小值是 .其中正确结论有( )
A.2个 B.3个 C.4个 D.5个
二、填空题
7.函数的图象的顶点坐标为 .
8.如图,线段AB的两个端点坐标分别为,.以原点O为位似中心,将线段AB缩小后得到线段DE,若,则端点D的坐标为 .
9.已知,则 .
10. 如图,在平面直角坐标系xOy中,⊙A切y轴于点B,且点A在反比例函数y(x>0)的图象上,连接OA交⊙A于点C,且点C为OA中点,则图中阴影部分的面积为 .
三、判断题
11.一幅图的比例尺是1:200000厘米。
12.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
13.如图,转盘分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字.三位同学发表了下述见解,正确的在括号内打“√”,错误的打“×”.
(1)甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形.( )
(2)乙:只要指针连续转六次,一定会有一次停在6 号扇形. ( )
(3)丙:在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.( )
14.圆的周长是直径的 π 倍.(判断对错)
四、计算题
15.若a:b=1:2,求(a+b):a的值.
16.
(1)计算:
(2)解方程:4x(x+3)=x2﹣9
17.解方程:
五、解答题
18.今年5月11日至12日,习近平总书记考察山西时指出,“要加强社区建设和管理,加强社区环境整治……,增强太原人民的获得感、幸福感、安全感”.随后,全市上下认真学习和贯彻这一重要指示精神,掀起了创建全国文明城市的高潮,学校学生会和校团委积极响应招募志愿者参加每周日进社区服务活动,小王、小华、小亮、小明四名同学主动报名,随机组成两个小组(每组各两人),到最近的两个社区进行服务,求小王和小华去同一个社区服务的概率.(画树状图或列表时,可用字母W,H,L,M分别代表小王、小华、小亮、小明四名同学)
19.如图,直线l1∥l2∥l3,直线AC依次交l1,l2,l3于A,B,C三点,直线DF依次交l1,l2,l3于D,E,F三点,若 ,DE=2,求EF的长.
20.为了让教师深入理解2022年版课程标准,某校开展了“学习新课标,践行新理念”活动,并组织了2022年版课程标准知识竞赛.甲、乙、丙、丁四名教师在这次校级竞赛活动中成绩优异,该校决定从这四名教师中随机选取两名教师参加市级2022年版课程标准知识竞赛.
(1)“甲、戊两名教师被选到”是 (填“随机”、“必然”或“不可能”)事件.
(2)请用列表或画树状图的方法,求恰好选到甲、乙两名教师的概率.
六、作图题
21.如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 ,请按下列要求画图:
(1)将 先向右平移4个单位长度、再向下平移5个单位长度,得到 ,画出 ,并写出点 的坐标;
(2)以点 为位似中心将 放大2倍,得到 ,画出 并写出点B的坐标.
七、综合题
22.如图,已知二次函数y=ax +bx+c的图象与x轴交于点A、B,与y轴交于点C.
(1)写出A、B、C三点的坐标;
(2)求出二次函数的解析式.
23.一只不透明的袋子里装有2个白球,1个黑球和若干个红球,这些球除颜色外都相同,从中任意摸出1个球,是红球的概率为 .
(1)袋子里红球有 个;
(2)现从袋子中一次摸出两个球,请用树状图或列表的方法列出所有等可能的结果,并求摸到的两个球中有一个是黑球的概率.
24.如图,在△OAB中,∠OAB=90°,OA=AB=6,将△OAB绕点O逆时针方向旋转90°得到△OA1B1.
(1)线段A1B1的长是 ;∠AOB1的度数是 .
(2)连接AA1,求证:四边形OAA1B1是平行四边形.
25.已知:如图,正方形的边长为1,在射线AB上取一点E,联结DE,将ADE绕点D针旋转90°,E点落在点F处,联结EF,与对角线BD所在的直线交于点M,与射线DC交于点N.求证:
(1)当时,求的值;
(2)当点E在线段AB上,如果,,求y关于x的函数解析式,并写出定义域;
(3)联结AM,直线AM与直线BC交于点G,当时,求AE的值.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定
2.【答案】C
【知识点】概率公式
3.【答案】B
【知识点】二次函数y=a(x-h)^2+k的图象
4.【答案】B
【知识点】二次函数图象与系数的关系
5.【答案】B
【知识点】一次函数图象、性质与系数的关系
6.【答案】C
【知识点】三角形全等及其性质;三角形全等的判定;正方形的性质;相似三角形的判定与性质
7.【答案】
【知识点】二次函数y=a(x-h)^2+k的图象
8.【答案】(1,1)
【知识点】位似变换
9.【答案】
【知识点】比例的性质
10.【答案】2
【知识点】扇形面积的计算;反比例函数图象上点的坐标特征;几何图形的面积计算-割补法
11.【答案】错误
【知识点】比例尺
12.【答案】(1)正确
(2)错误
【知识点】垂径定理
13.【答案】(1)错误
(2)错误
(3)错误
【知识点】事件发生的可能性
14.【答案】正确
【知识点】圆的认识
15.【答案】解:∵a:b=1:2,
∴b=2a,
∴(a+b):a=(a+2a):a=3.
【知识点】比例的性质
16.【答案】(1)解:原式=2﹣2× +| ﹣1|+1
=2﹣ + ﹣1+1
=2;
(2)解:方程整理得:4x2+12x=x2﹣9,即x2+4x+3=0,
分解因式得:(x+1)(x+3)=0,
可得x+1=0或x+3=0,
解得:x1=﹣1,x2=﹣3.
【知识点】零指数幂;负整数指数幂;特殊角的三角函数值
17.【答案】解:
或
或
【知识点】因式分解法解一元二次方程
18.【答案】解:画树状图如下图:
共有12种等可能的结果,其中小王和小华去同一个社区服务的结果有4个,
∴小王和小华去同一个社区服务的概率为: .
【知识点】列表法与树状图法;复合事件概率的计算
19.【答案】解:∵l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,
∴ ,
∵ ,DE=2,
∴ ,
解得:DF=3.5,
∴EF=DF-DE=3.5-2=1.5
【知识点】平行线分线段成比例
20.【答案】(1)不可能
(2)
【知识点】随机事件;列表法与树状图法;概率的简单应用
21.【答案】(1)解:根据题意可得:
∴
(2)解:根据题意可得:
∴
【知识点】作图﹣平移;作图﹣位似变换
22.【答案】(1)A、B、C三点的坐标为A(-1,0),B(4,0),C(0,-3
(2)解:把A(-1,0),B(4,0),C(0,-3)代入y=ax2+bx+c可得
,
解得
∴y=
【知识点】待定系数法求二次函数解析式
23.【答案】(1)2
(2)解:画树状图如图:
共有20个等可能的结果,摸到的两个球中有一个是黑球的结果有8个,
∴摸到的两个球中有一个是黑球的概率为 .
【知识点】概率公式;等可能事件的概率
24.【答案】(1)6;135°
(2)解:∵∠A1OA=∠OA1B1=90°,∴A1B1∥OA,
又∵OA=AB=A1B1
∴四边形OAA1B1是平行四边形.
【知识点】平行四边形的判定;旋转的性质
25.【答案】(1)解:过点E作EH⊥BD与H,
∵正方形的边长为1,,
∴EB=1-,
∵BD为正方形对角线,
∴BD平分∠ABC,
∴∠ABD=45°,
∵EH⊥BD,
∴∠BEH=180°-∠EBH-∠EHB=180°-45°-90°=45°,
∴EH=BH,
∴EH=BH=BEsin45=,AB=BDcos45°,
∴,
∴DH=DB-BH=,
;
(2)解:如上图,∵AE=x,
∴BE=1-x,
∵将△ADE绕点D针旋转90°,得到△DCF,
∴CF=AE=x,ED=FD=,
∴BF=BC+CF=1+x,
在Rt△EBF中EF=,
∵∠EDF=90°,ED=FD,
∴△DEF为等腰直角三角形,
∴∠DFE=∠DEF=45°,
∴∠EBM=∠MFD=45°,
∵∠EMB=∠DMF,
∴△BEM∽△FDM,
∴,即,
∵∠DEM=∠FBM=45°,∠EMD=∠BMF,
∴△EMD∽△BMF,
∴,即,
∴,
∴,
∴即,
∴,0≤x≤1
(3)解:当点G在BC上,,
∵四边形ABCD为正方形,
∴AD∥BG,
∴∠DAM=∠BGM,∠ADM=∠GBM,
∴△BGM∽△DAM,
∴,
∵由(2)知△BEM∽△FDM,
∴,
∵DB=,
∴,
∴,
∴,
∵,
∴即,
解,舍去;
当点G在CB延长线上,,过M作ML⊥BC,交直线BC于L,
∵GB∥AD,
∴∴∠DAM=∠BGM,∠ADM=∠GBM,
∴△BGM∽△DAM,
∴,
∴,
∴,
∵∠LBM=∠CBD=45°,ML⊥BC,
∴△MLB为等腰直角三角形,
∵ML∥CD,
∴∠LMB=∠CDB,∠L=∠DCB,
∴△MLB∽△DCB,
∴,CD=1,
∴ML=
∵ML∥BE,
∴∠L=∠FBE,∠LMF=∠BEF,
∴△LMF∽△BEF,
∴,
∵BE=AE-AB=x-1,LF=LB+BC+CF=,BF=BC+CF=1+x,
∴,
整理得:,
解得,舍去,
∴AE的值为或.
【知识点】正方形的性质;相似三角形的判定与性质;旋转的性质;四边形的综合
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
