事件的概率3
图片预览





文档简介
课件14张PPT。23.3 用列举法求概率(3)复习引入 等可能试验的两个特征:
1.试验的结果是有限个;
2.任何两个结果不可能同时出现,即发生的可能性相等; 如果一个试验共有n个等可能的结果,事
件A包含其中的k个结果,那么事件A的概率 探究 1、木盒里有1个红球和1个绿球,这两个球除颜色外其它都相同,从盒子里先摸出一个球,放回去摇匀后,再摸出一个球。
(1)两次都摸到红球的概率是多少?
(2)摸到1个红球和1个绿球的概率又是多少?有人说,两次摸球只有三种可能的结果:
2红、2绿、1红1绿。所有摸到2红的
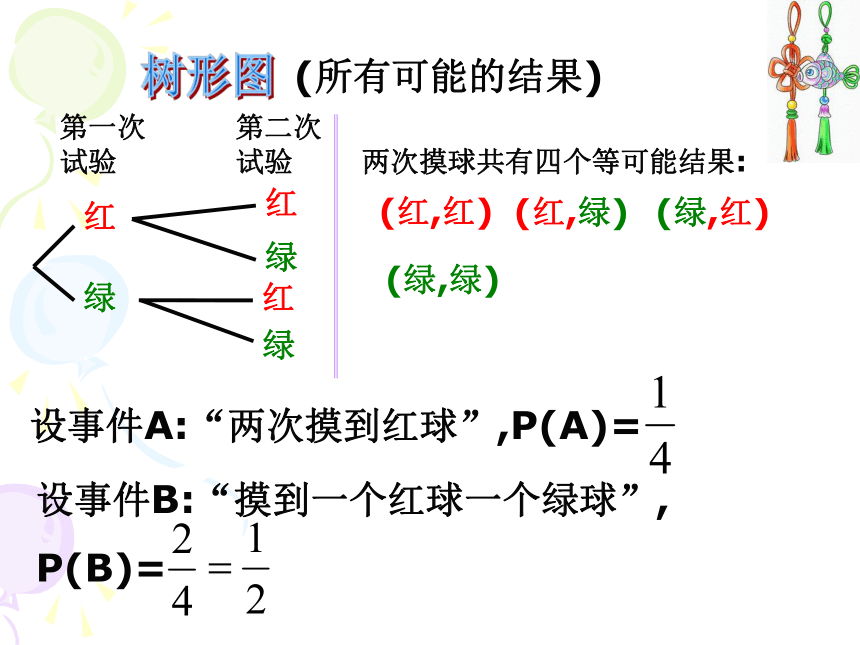
概率与1红1绿的概率都应该是 ,对吗?问题 在分析一些较为复杂的等可能试验时,如何才能不重复不遗漏地列出所有结果呢?列举法画“数形图”树形图(所有可能的结果)第一次试验第二次试验两次摸球共有四个等可能结果:(红,红)(红,绿)(绿,红)(绿,绿)设事件A:“两次摸到红球”,P(A)=设事件B:“摸到一个红球一个绿球”,
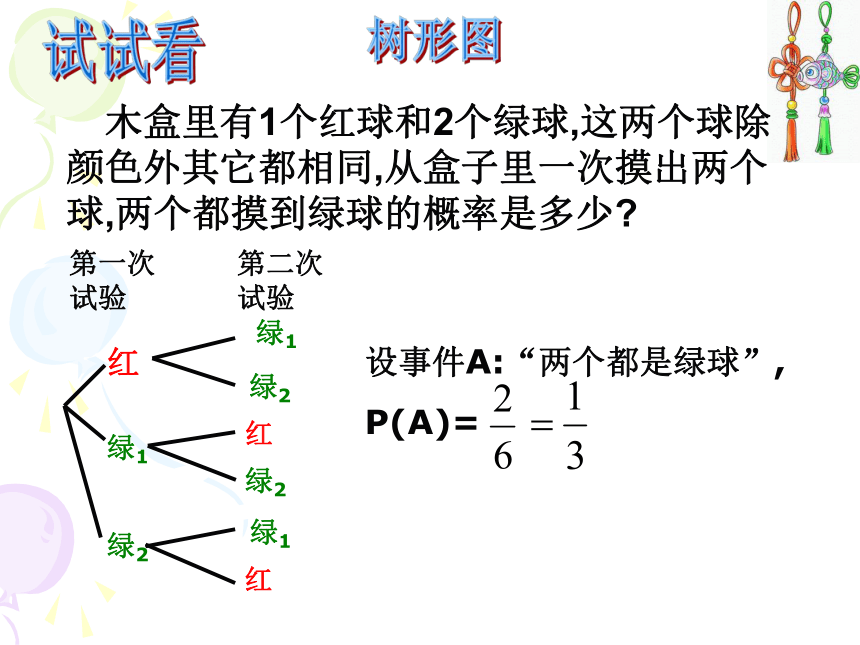
P(B)=方法小结试试看 木盒里有1个红球和2个绿球,这两个球除颜色外其它都相同,从盒子里一次摸出两个球,两个都摸到绿球的概率是多少?树形图第一次试验红绿1第二次试验绿2设事件A:“两个都是绿球”,
P(A)=例:甲乙两个同学做“石头、剪刀、布”的游戏,在一个回合中两人能分出胜负的概率是多少? 两人手势相同的结果有3个,不分胜负,其余6个能分胜负设事件A:“两人能分出胜负”,则P(A)=随堂练习1.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则设事件A:“穿同一双袜子”,则P(A)=要“玩”出水平“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是:“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)行家看“门道” 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.用心领“悟”解:每次游戏时,所有可能出现的结果如下:游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)小结1等可能试验结果的分析方法:线段法;树形图;表格法
2树形图要注意:分级画树枝要从左往右或由上而下;同一级的每个树枝都等可能;最后一级的树枝数等于所有等可能的结果数
1.试验的结果是有限个;
2.任何两个结果不可能同时出现,即发生的可能性相等; 如果一个试验共有n个等可能的结果,事
件A包含其中的k个结果,那么事件A的概率 探究 1、木盒里有1个红球和1个绿球,这两个球除颜色外其它都相同,从盒子里先摸出一个球,放回去摇匀后,再摸出一个球。
(1)两次都摸到红球的概率是多少?
(2)摸到1个红球和1个绿球的概率又是多少?有人说,两次摸球只有三种可能的结果:
2红、2绿、1红1绿。所有摸到2红的
概率与1红1绿的概率都应该是 ,对吗?问题 在分析一些较为复杂的等可能试验时,如何才能不重复不遗漏地列出所有结果呢?列举法画“数形图”树形图(所有可能的结果)第一次试验第二次试验两次摸球共有四个等可能结果:(红,红)(红,绿)(绿,红)(绿,绿)设事件A:“两次摸到红球”,P(A)=设事件B:“摸到一个红球一个绿球”,
P(B)=方法小结试试看 木盒里有1个红球和2个绿球,这两个球除颜色外其它都相同,从盒子里一次摸出两个球,两个都摸到绿球的概率是多少?树形图第一次试验红绿1第二次试验绿2设事件A:“两个都是绿球”,
P(A)=例:甲乙两个同学做“石头、剪刀、布”的游戏,在一个回合中两人能分出胜负的概率是多少? 两人手势相同的结果有3个,不分胜负,其余6个能分胜负设事件A:“两人能分出胜负”,则P(A)=随堂练习1.小明是个小马虎,晚上睡觉时将两双不同的袜子放在床头,早上起床没看清随便穿了两只就去上学,问小明正好穿的是相同的一双袜子的概率是多少?解:设两双袜子分别为A1、A2、B1、B2,则设事件A:“穿同一双袜子”,则P(A)=要“玩”出水平“配紫色”游戏小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.(1)利用列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少?
真知灼见源于实践表格可以是:“配紫色”游戏游戏者获胜的概率是1/6.黄蓝绿红(红,黄)(红,蓝)(红,绿)白(白,黄)(白,蓝)(白,绿)行家看“门道” 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.用心领“悟”解:每次游戏时,所有可能出现的结果如下:游戏者获胜的概率为1/6.112(1,1)(1,2)2(2,1)(2,2)3(1,3)(2,3)小结1等可能试验结果的分析方法:线段法;树形图;表格法
2树形图要注意:分级画树枝要从左往右或由上而下;同一级的每个树枝都等可能;最后一级的树枝数等于所有等可能的结果数
