命题的形式及等价关系

教案 四种命题的形式及等价关系（二）
教学目标：
（1）进一步理解四种命题之间的相互关系，能根据原命题准确地写出它的逆命题、否命题和逆否命题三种形式；
（2）正确理解等价命题的概念，以及原命题的真假与它的逆命题、否命题和逆否命题的真假之间的关系；
（3）通过对四种命题之间关系的学习，培养学生逻辑思维能力。
教学重点：四种命题及其关系以及等价命题。
教学难点：对四种命题的理解及应用。
教学过程：
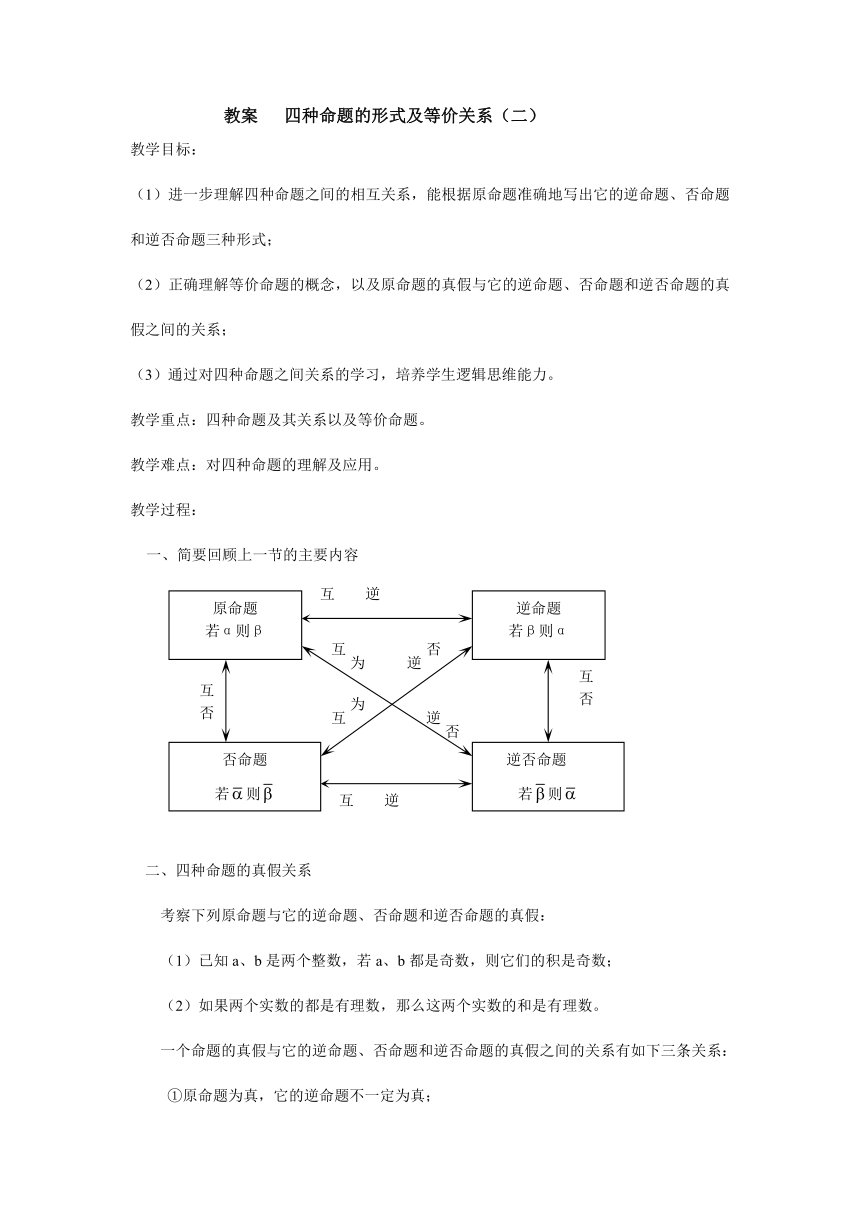
1、 简要回顾上一节的主要内容
二、四种命题的真假关系
考察下列原命题与它的逆命题、否命题和逆否命题的真假：
（1）已知a、b是两个整数，若a、b都是奇数，则它们的积是奇数；
（2）如果两个实数的都是有理数，那么这两个实数的和是有理数。
一个命题的真假与它的逆命题、否命题和逆否命题的真假之间的关系有如下三条关系：
①原命题为真，它的逆命题不一定为真；
②原命题为真，它的否命题不一定为真；
③原命题为真，它的逆否命题一定为真。
定义：两个命题A、B，如果AB且BA，就称A和B为等价命题。
例1、判断下列命题的真假，并说明理由。
（1）若一元二次方程ax2+bx+c=0(a≠0) 满足ac<0，那么这个方程有实数根；
（2）若一元二次方程ax2+bx+c=0(a≠0) 有实数根，那么满足ac<0；
（3）设a、b、c∈N*，如果ab是c的倍数，那么a、b中至少有一个是c的倍数。
例2、已知BD、CE分别是△ABC的∠B、∠C的角平分线，而且BD≠CE。
求证：AB≠AC。
例3设两个一元二次方程ax2+2bx+1=0和cx2+2dx+1=0（其中a、b、c、d均为实数）满足a+c=2bd。求证：上述两个方程中至少有一个方程有实数根。
反证法：
要证明某一结论A是正确的，但不直接证明，而是先去证明A的反面（非A）是错误的，从而断定A是正确的即反证法就是通过否定命题的结论而导出矛盾来达到肯定命题的结论，完成命题的论证的一种数学证明方法。
反证法的步骤：
(1)假设命题的结论不成立，即假设结论的反面成立。
(2)从这个假设出发，通过推理论证，得出矛盾。
(3)由矛盾判定假设不正确，从而肯定命题的结论正确。
注意：可能出现矛盾四种情况：
①与题设矛盾；②与反设矛盾；③与公理、定理矛盾④在证明过程中，推出自相矛盾的结论
练习p19练习1.4（3）
3、 布置作业：练习册p6习题1.4B组1至4.
补充：
1．命题“若，则x=y2+1”的逆命题是________命题（填“真”或“假”）
2．“方程x2-ax+2=0(a∈R)有两个相同符号的实根”是______命题（填“真”或“假”）
3． “若a是被3除余2的正整数，则a∈{x|x=3k+2，k∈N*}”是______命题（填“真”或“假”），理由是_______________________________。
4．写出一个与命题“AB”等价的命题__________________________________。
5．若三条线段不能够构成一个三角形，则 （ ）
（A）任意两条线段的长度之和不大于第三条线段的长度；
（B）必有两条线段的长度之和小于第三条线段的长度；
（C）必有两条线段的长度之差不小于第三条线段的长度；
（D）不存在两条线段的长度之差小于第三条线段的长度。
6．与命题“x、y、z不全为负数”等价的命题是 （ ）
（A）x、y、z中至少有一个是正数；
（B）x、y、z全不是负数；
（C）x、y、z中只有一个是负数；
（D）x、y、z中至少有一个是非负数。
7．命题M：ax+b=cx+d，命题N：，则命题M与N的推出关系是 （ ）
（A）NM （B）MN （C）MN （D）以上都不对
8．命题A成立可推出命题B不成立，那么下列说法正确的是 （ ）
（A）命题A成立可推出命题B成立；
（B）命题A不成立可推出命题B不成立；
（C）命题B不成立可推出命题A成立；
（D）命题B成立可推出命题A不成立。
7．判断命题“三个连续的正整数的和是3的倍数“的真假，并说明理由。
8．求证：若abc≠1，则a≠1或b≠1或c≠1。
9．在ΔABC中，D是BC的中点，求证：若，则AB、AC不垂直。
否
否
逆
为
互
互
否
互 逆
逆否命题
若则
否命题
若则
逆命题
若β则α
原命题
若α则β
互 逆
互
互
否
逆
为