相似三角形的应用
图片预览



文档简介
课件16张PPT。相似三角形 的应用
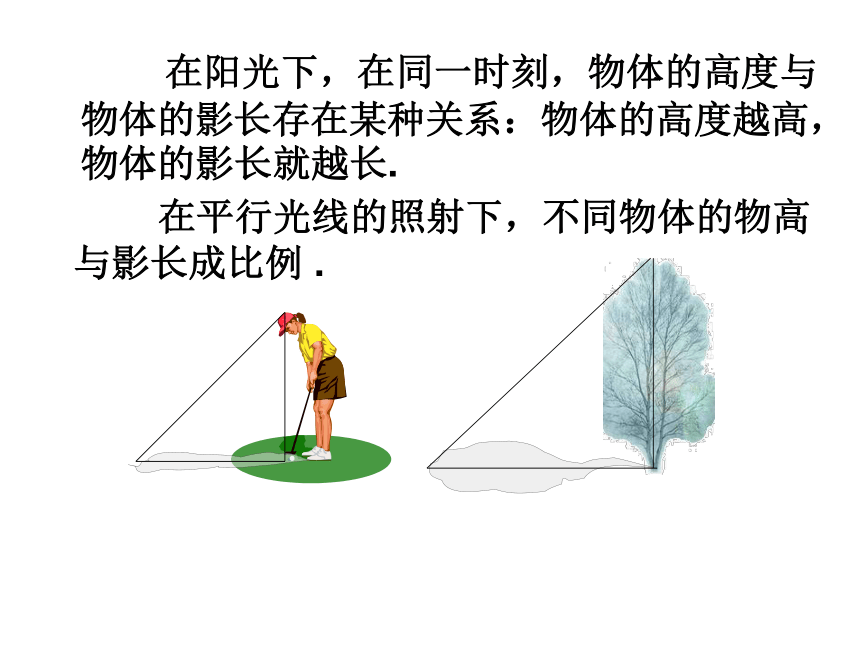
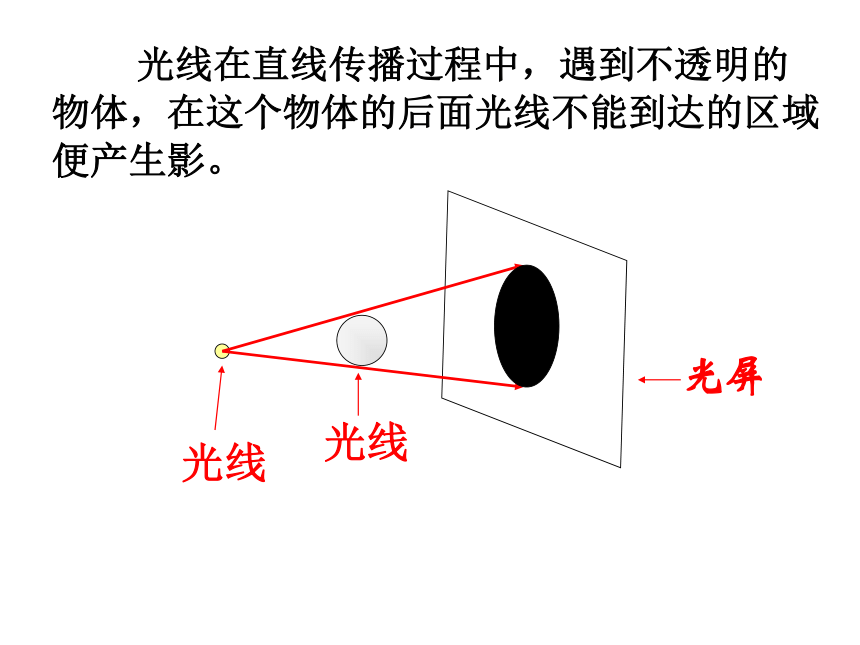
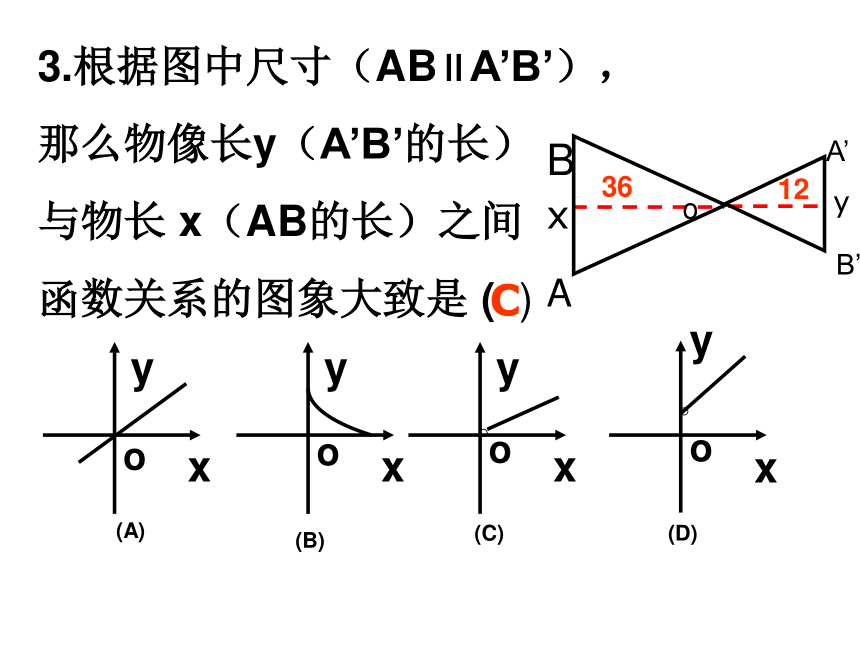
在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长. 在平行光线的照射下,不同物体的物高与影长成比例 .光屏 光线在直线传播过程中,遇到不透明的物体,在这个物体的后面光线不能到达的区域便产生影。 光线光线1 .一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为( ) A.7.5米 B.8米 C.14.7米 D.15.75米 2.在某一刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?A363.根据图中尺寸(AB∥A’B’),
那么物像长y(A’B’的长)
与物长 x(AB的长)之间
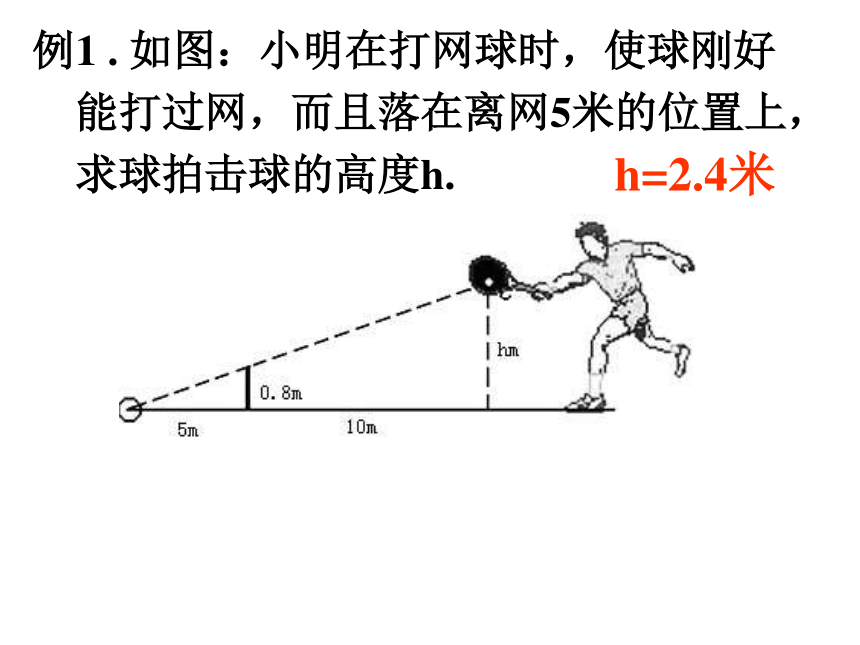
函数关系的图象大致是 ( )yB’36BAA’12oxyC例1 . 如图:小明在打网球时,使球刚好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.h=2.4米 例2.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,
EC=50米,求两岸间的大致距离AB. AB=100米例3.如图:某社区准备2000元计划在一块上底、下底分别是10米、20米的梯形的空地上种植花卉,他们想在△ AMD和△ BMC地带种植10元/m2的太阳花,当△ AMD地带种满花后已经花了500元,请你预算一下,若继续在△ BMC地带种植同样的花,资金是否够用,说明理由.不够 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成正方形零件,使正方形的一边QM在BC上,其余两个顶点P、N分别在AB、AC上,这个正方形PQMN的边长是多少?面积是多少?解:设正方形的边长为Xcm.∵PN∥BC
∴△APN∽△ABCS正=4.8×4.8=23.04cm2A解:设PQ=x,PN=y,则AE=8-x∵PN∥BC
∴△APN∽△ABC(0家庭作业:创新教育P 48-49努力现在,成就未来
在阳光下,在同一时刻,物体的高度与物体的影长存在某种关系:物体的高度越高,物体的影长就越长. 在平行光线的照射下,不同物体的物高与影长成比例 .光屏 光线在直线传播过程中,遇到不透明的物体,在这个物体的后面光线不能到达的区域便产生影。 光线光线1 .一根1.5米长的标杆直立在水平地面上,它在阳光下的影长为2.1米;此时一棵水杉树的影长为10.5米,这棵水杉树高为( ) A.7.5米 B.8米 C.14.7米 D.15.75米 2.在某一刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?A363.根据图中尺寸(AB∥A’B’),
那么物像长y(A’B’的长)
与物长 x(AB的长)之间
函数关系的图象大致是 ( )yB’36BAA’12oxyC例1 . 如图:小明在打网球时,使球刚好能打过网,而且落在离网5米的位置上,求球拍击球的高度h.h=2.4米 例2.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,
EC=50米,求两岸间的大致距离AB. AB=100米例3.如图:某社区准备2000元计划在一块上底、下底分别是10米、20米的梯形的空地上种植花卉,他们想在△ AMD和△ BMC地带种植10元/m2的太阳花,当△ AMD地带种满花后已经花了500元,请你预算一下,若继续在△ BMC地带种植同样的花,资金是否够用,说明理由.不够 如图,△ABC是一块锐角三角形余料,边BC=12cm,高AD=8cm,要把它加工成正方形零件,使正方形的一边QM在BC上,其余两个顶点P、N分别在AB、AC上,这个正方形PQMN的边长是多少?面积是多少?解:设正方形的边长为Xcm.∵PN∥BC
∴△APN∽△ABCS正=4.8×4.8=23.04cm2A解:设PQ=x,PN=y,则AE=8-x∵PN∥BC
∴△APN∽△ABC(0
